起伏地形條件下二維大地電磁各向異性正演

王 寧， 肖 曉， 張逗逗

(1.中南大學 地球科學與信息物理學院，長沙 410083；2.中南大學 有色金屬成礦預測教育部重點實驗室, 長沙 410083)

起伏地形條件下二維大地電磁各向異性正演

王 寧1,2， 肖 曉1,2， 張逗逗1,2

(1.中南大學 地球科學與信息物理學院，長沙 410083；2.中南大學 有色金屬成礦預測教育部重點實驗室, 長沙 410083)

在大地電磁資料處理和解釋中，大地電磁的各向異性正演一直是國內、外研究的前沿課題。這里首先從麥克斯韋方程組出發，得出各向異性介質二維大地電磁場的邊值問題以及等價的變分問題，進而對計算區域進行完全非結構化三角形剖分，在單元內采用線性插值，將變分方程轉化成線性方程組，求解出有限單元法數值解，獲得各向異性介質下的電磁場值。討論了電性主軸與笛卡爾坐標軸之間的夾角以及地形的起伏變化對視電阻率和相位值的影響，結果表明：起伏地形條件下，TE和TM兩種極化模式的視電阻率和相位值都會受到影響，且TM模式受地形影響較大；由于介質的各向異性，視電阻率和相位斷面圖出現明顯不同于各向同性的形態，導致橫向分界面模糊。

大地電磁； 有限單元法； 各向異性； 起伏地形

0 引言

大地電磁測深法(Magnetotelluric Sounding Method)是利用天然電磁場源，研究地殼及上地幔電性結構的一種重要的地球物理勘探方法[1-2]。但由于地球構造應力場、地球形變帶、巖石裂隙、空隙水及地質沉積等因素造成的地球各向異性問題[3]，對大地電磁勘探數據準確合理地解釋造成極大的困難，因而各向異性研究備受國內、外地球物理學家的關注。O'Brien 等[4]推導了層狀各向異性電磁場計算的遞推公式，由此開啟了大地電磁各向異性研究的大門 ； Pek等[5]推出了一種聯合計算一般層狀各向異性介質中大地電磁阻抗張量和參數靈敏度矩陣的算法。在大地電磁二維各向異性正演問題中，有限單元法、有限差分法和特殊情況下解析解法是主要的研究方法。有限差分方面， Saraf 等[6]用有限差分法計算了均勻半空間中嵌入一個水平和垂直方向電導率不同的異常體時的H偏振模式； Pek等[7]推導出了全張量電導率的電磁場偏微分方程，并且應用有限差分法對任意各向異性介質進行了正演計算；霍光譜等[8]利用Pek[7]的求解方法研究了起伏地形條件下，各向異性對大地電磁實測資料的影響。但傳統有限差分采用矩形網格，這將導致該方法在擬合地形及復雜地質構時不能完成很好的模擬。Reddy 等[9]率先使用伽遼金有限元法對二維各向異性問題中的偏微分方程做了數值計算；徐世浙等[10]用有限元法計算了二維各向異性地電斷面的大地電磁場；李予國[11]在前人的基礎上給出了任意各向異性地質體的感應電磁場的有限元離散公式；熊彬等[12-13]用有限元法模擬了二維各向異性MT響應，并且討論了層面傾角和頻率對低電阻率的影響；秦林江等[14-15]采用Fourier變化的方法獲得了對角各向異性無限深斷裂的MT響應函數的解析解，并對解析解計算過程中的精度問題進行了討論，同時對實測電磁資料中遇到的兩支視電阻率在無窮遠處不一致的現象給出了解釋；田紅軍等[16]討論了起伏地形和各向異性對大地電磁測深中TM極化模式響應的影響規律。

目前國內各向異性的正演模擬中大多使用的是結構化網格[12-16]，但是該網格在處理復雜構造和地形問題時很難完成精確地模擬。筆者采用非結構化網格[18-21]有限單元法，對大地電磁中常見的電性主軸其中一個方向與走向一致的二維各向異性體結構[10,12-16]進行正演模擬，研究視電阻率和相位值隨其他兩個電性主軸與笛卡爾坐標軸夾角α的變化規律，以及地形對視電阻率和相位值的影響。

1 變分問題

1.1 基本理論

由電磁場理論可知，電磁波在介質中的傳播遵從麥克斯韋方程組[1-2,17]：

▽×E=iωμH

(1)

▽×H=(σ-iωμε)E

(2)

式中：E、H分別是電場強度矢量和磁場強度矢量；ω=2πf是角頻率，對于大地電磁法所涉及的頻率，巖石中σ>>ωε，因而可以忽略介電常數的各向異性，筆者只考慮電導率的各向異性，因而電導率σ是張量。空氣以及地下介質的導磁率和介電常數分別取μ=μ0=4π×10-7，ε=ε0=8.85×10-12。對于各向異性介質，可以找到一個坐標系ikm(圖1)，使張量電導率化為對角矩陣形式：

(3)

其中：σi、σk、σm分別為電性主軸方向上的電導率。

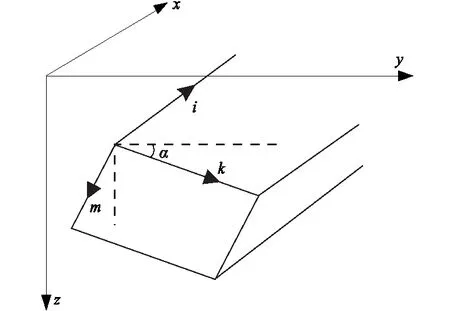
圖1 各向異性主軸與笛卡爾坐標系Fig.1 Anisotropic principal direction and Cartesian coordinate system

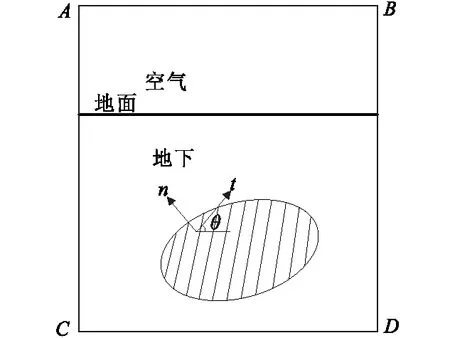
圖2 邊界條件Fig.2 The boundary conditions

我們考慮的各向異性模型的電性主軸i與笛卡爾坐標系中的x方向一致，而互相正交的電性主軸k、m與y、z坐標軸成一角度α。按照張量在不同坐標系中的變換公式，在xyz坐標系中，電導率張量σ可表示為：

σ=Aσ′AT

其中:A為坐標變換張量：

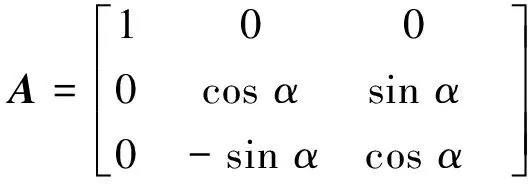
(4)

TE極化模式：

(5)

TM極化模式：

(6)

式(5)和式(6)可以統一寫成式(7)。

▽·(τ▽u)+λu=0

(7)

式中：▽為二維哈密頓算符。

1.2 邊界條件

二維各向異性介質大地電磁場兩種極化模式下滿足的邊值問題為：

(8)

1.3 變分問題

與邊值問題等價的變分問題為式(9)～式(11)。

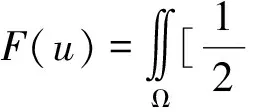
(9)

u|AB=1

(10)

δF(u)=0

(11)

2 有限單元法

筆者采用開源程序triangle將求解區域Ω自動剖分成三角形單元，對于三角單元e，采用線性基函數，u表示為式(12)。

u=Niui+Njuj+Nmum

(12)

其中：

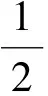
式中(yk,zk)(k=i,j,m)為三角形單元頂點的坐標。

最終得到的線性方程組為式(13)。

Ku=0

(13)

采用乘大數法，加載式(8)中AB邊界條件，形成右端項，得到大型稀疏方程組。對方程組采用Eigen中的直接求解器PardisoLU來求解線性方程組。

為了計算視電阻率還需要知道地面測點上的Ey和Hy，由式(5)、式(6)有：

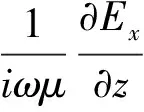
(14)

(15)

采用四點差分求得相應的磁場Hy和電場Ex，即可求出視電阻率和相位值：

TE模式：

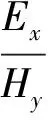
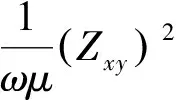
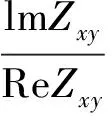
TM模式：

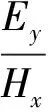
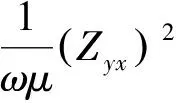
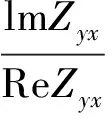
3 正演結果分析

3.1 程序驗證

筆者采用c語言編寫了相應的正演程序。為了驗證程序的精度和可靠性， 以標準模型COMMEMI 2D-1作為驗證模型(圖3)，選用頻率f=10 Hz，與開源程序MT2D(https:// sourceforge.net/projects/mt2d/)計算結果進行對比，結果如圖4所示。TE模式下，二者視電阻率相對誤差在0.22%以內，相位差在0.35°以內；TM模式下，二者視電阻率相對誤差在0.34%以內，相位差在0.39°以內。

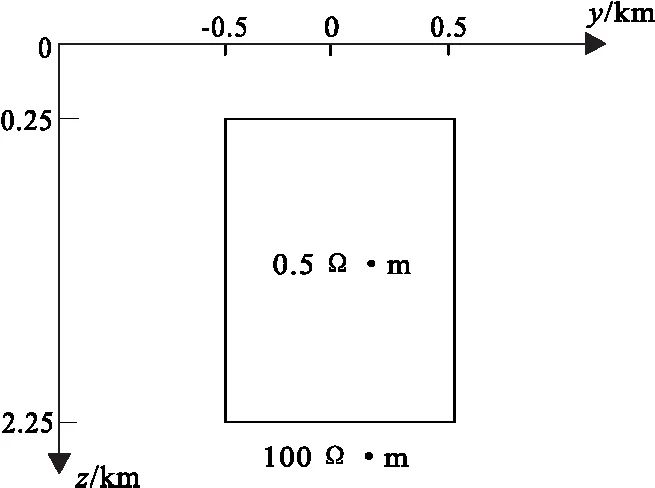
圖3 2D-1模型Fig.3 The 2D-1 model

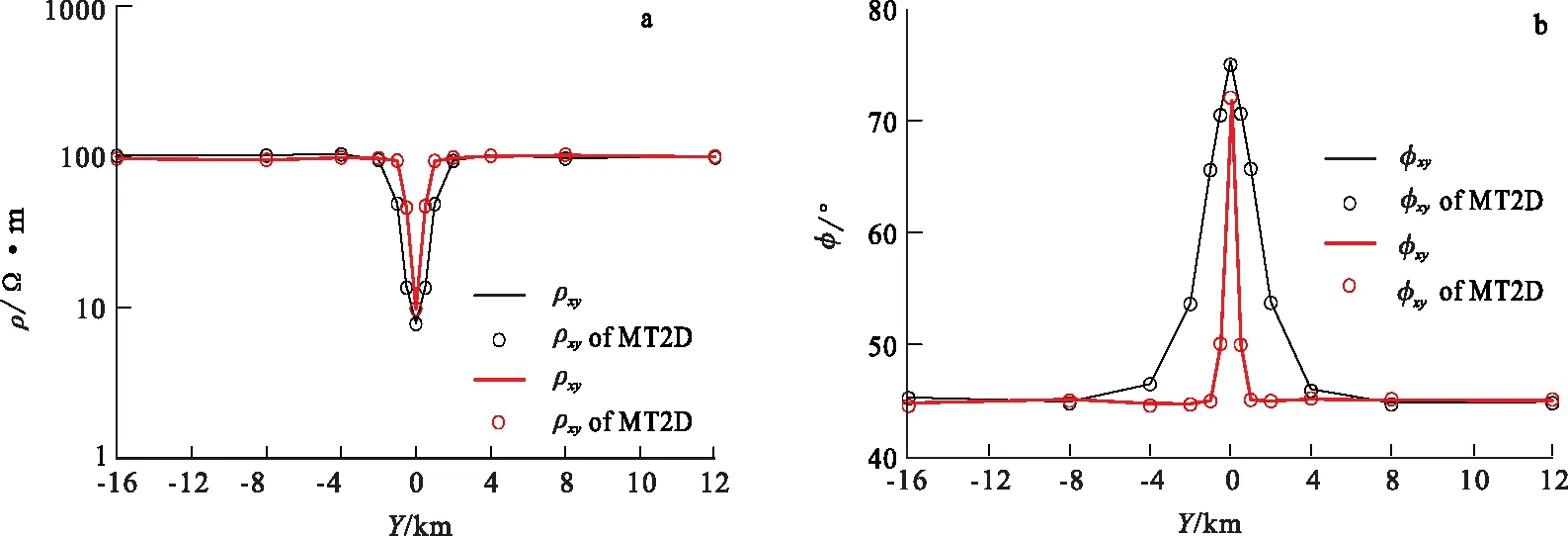
圖4 程序結果驗證Fig.4 Comparison of the results with MT2D(a)視電阻率對比圖；(b)相位對比圖

3.2 不同傾角對MT響應的影響

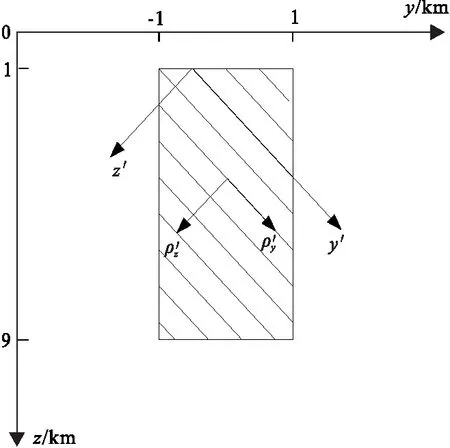
圖5 二維各向異性模型Fig.5 The two-dimensional anisotropic model

從圖6可以看出，TE模式視電阻率和相位均不隨夾角α而變。但TM模式視電阻率和相位值隨著夾角α變化有很大的差異：在α=0°和α=90°時，視電阻率和相位值左右兩端對稱；在α=30°和α=60°時，視電阻率和相位值左右兩端不對稱。在無窮遠處，不同夾角下的視電阻率值均趨于均勻半空間的值，而相位值趨于45°。

3.3 在起伏地形下不同夾角的對比模型

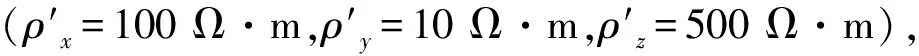
由圖6可知，α對 TE模式的視電阻率和相位值都沒有影響，故圖8只給出α=0°時三種模型的視電阻率和相位擬斷面圖。圖8(a)是無地形時視電阻率擬斷面圖，圖中顯示有一個低阻的閉合；圖8(b)由于地壘模型的存在，使得地壘頂部覆蓋范圍內視電阻率值有所增加；圖8(c)由于地塹模型的存在，使得地塹底部覆蓋范圍內電阻率值有所減小。從圖8(d)～圖8(f)中可以看出，高頻段相位高于低頻段，地壘模型減小了高低頻段的相位差值，地塹增大了這種差異。

圖9是TM模式下的視電阻率和相位擬斷面圖。從圖9(a)中可以看出：當α=0°和α=90°時，異常體橫向分界面明顯，是左右對稱的低阻異常體；當α=30°和α=60°時，異常體橫向分界面不再明顯，在左側出現低阻的異常，而右側，顯示高阻的異常；在地壘頂部覆蓋范圍內，視電阻率明顯減小，在地壘與平面交界處有明顯的高阻異常，在地塹底部覆蓋范圍內，視電阻率明顯增大，而在地塹與平地面交界處有明顯的低阻異常。從圖9(b)中可以看出：α=0°和α=90°時，相位橫向分界面明顯，且是左右對稱；當α=30°和α=60°時，在左側顯示高相位，而右側顯示低相位。地形對相位也有一定的影響，但是影響的數值比較小。

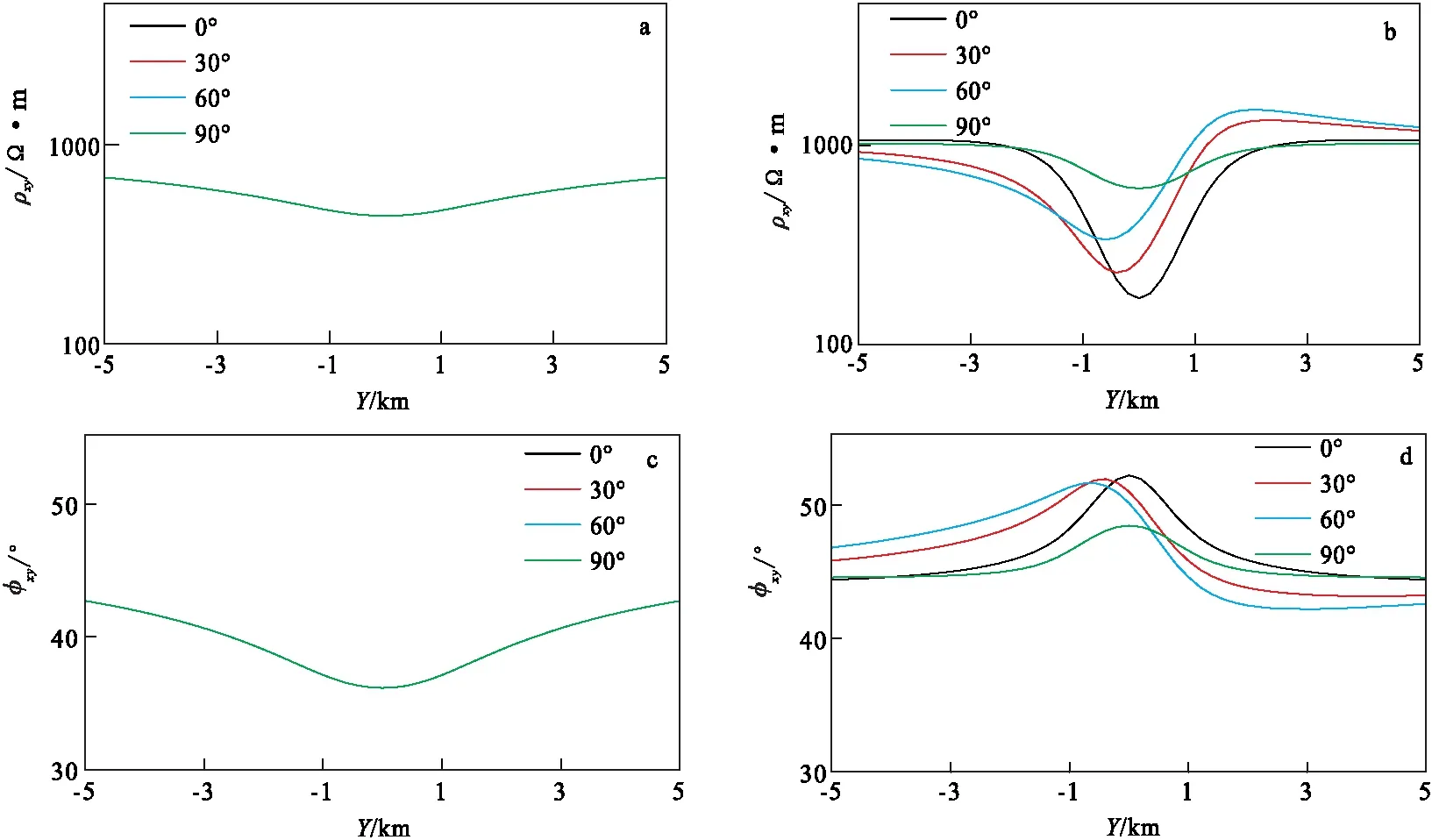
圖6 不同夾角對應的視電阻率和相位值(頻率為1 Hz)Fig.6 Corresponding the values of apparent resistivity and phase to different angles(with the frequency of 1 Hz)(a)TE模式下視電阻率；(b)TM模式下視電阻率；(c)TE模式下相位；(d)TM模式下相位

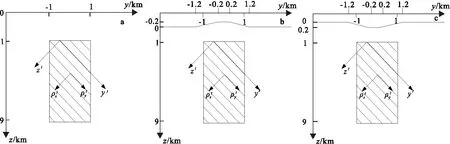
圖7 帶有起伏地形的二維各向異性模型Fig.7 2D anisotropic model with topography

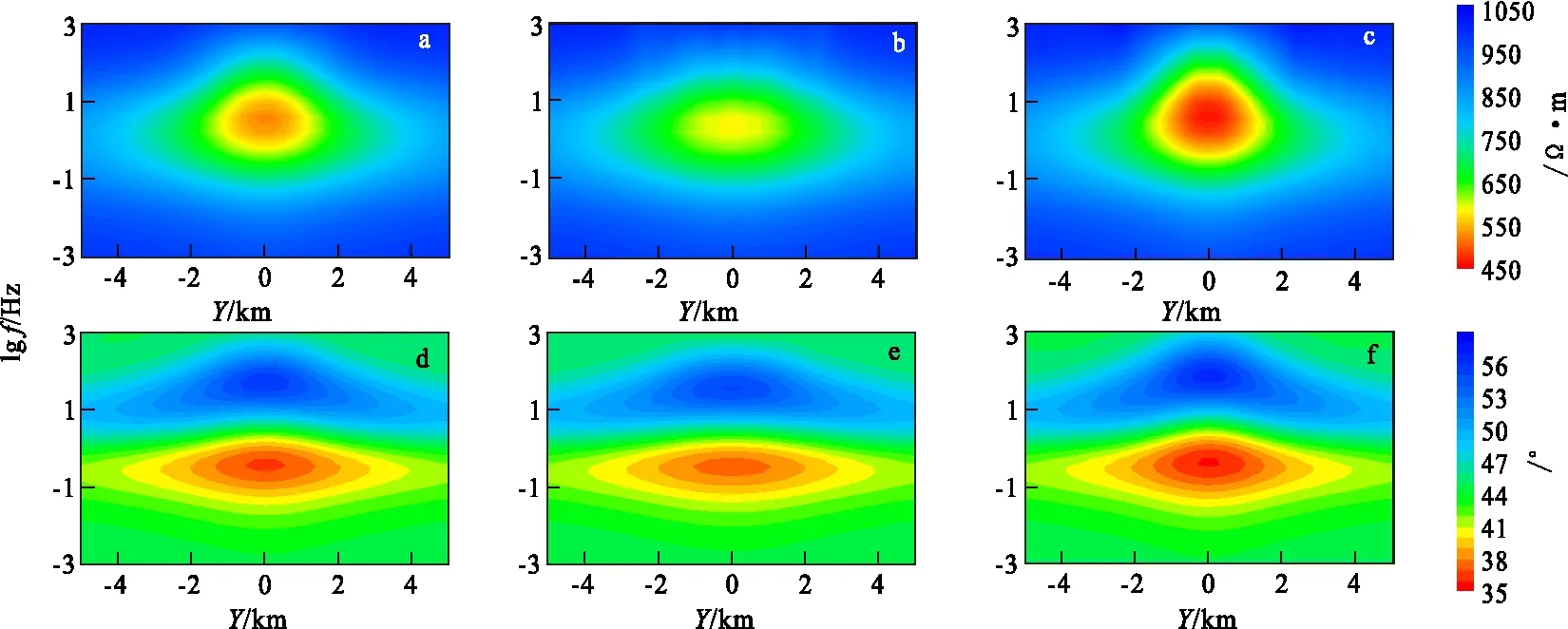
圖8 TE模式視電阻率和相位擬斷面圖Fig.8 Apparent resistivity and phase cross-section diagram of TE(a)水平地形視電阻率擬斷面圖;(b)地壘地形視電阻率擬斷面圖;(c)地塹地形視電阻率擬斷面圖;(d)水平地形相位擬斷面圖;(e)地壘地形相位擬斷面圖;(f)地塹地形相位擬斷面圖

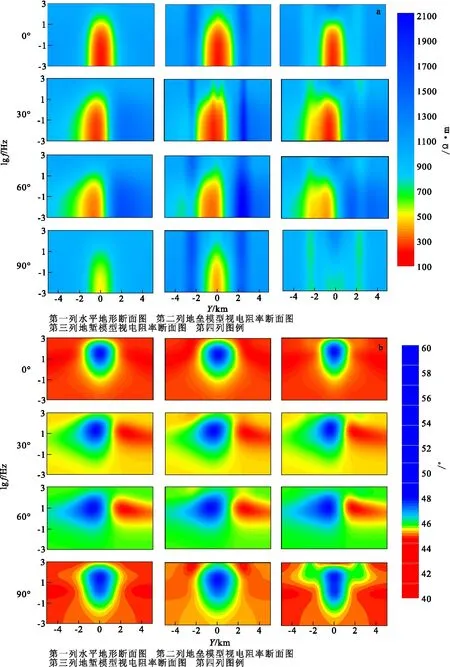
圖9 TM模式視電阻率和相位擬斷面圖Fig.9 Apparent resistivity and phase cross-section diagram of TM(a)視電阻率擬斷面圖；(b)相位擬斷面圖

4 結論

1)當α改變時，TE極化模式的視電阻率和相位保持不變，TM極化模式視電阻率和相位發生明顯變化：在α=0°和α=90°時，視電阻率和相位擬斷面圖是對稱的，且橫向分界面明顯；在α≠0°且α≠90°時，視電阻率和相位形態不再嚴格對稱，甚至出現很大的差異；橫向分界面也變得比較模糊。

2)起伏地形條件下，TE和TM兩種極化模式的視電阻率和相位都會受到影響，但地形對TM模式的影響較大，TE模式則受地形影響微弱。

3)對于TE極化模式，當電性主軸其中一個方向與走向一致時可以不考慮主軸夾角變化的影響，但對于TM極化模式，當起伏地形和各向異性同時存在時，二者的影響都應該考慮。

[1] TIKHONOV A N. On determining electric characteristics of the deep layers of the Earth's crust[J]. Sov.math.dokl, 1950, 73：295-297.

[2] CAGNIARD L. Basic theory of the magneto-telluric method of geophysical prospecting[J]. Geophysics, 2002, 18(3):605-635.

[3] 霍光譜, 胡祥云, 劉敏. 各向異性介質中大地電磁正演研究綜述[J]. 地球物理學進展, 2011, 26(6): 1976-1982.

HUO G P,HU X Y,LIU M. Review of the forward modeling of magnetotelluric in the anisotropy medium research[J]. Progress in Geophysics, 2011, 26(6): 1976-1982.( In Chinese)

[4] O'BRIEN D P,MORRISON H F. Electromagnetic fields in an n-layer anisotropic half-space[J].Geophysics,1967,32(4):668-677.

[5] PEK J, SANTOS F A M. Magnetotelluric impedances and parametric sensitivities for 1-D anisotropic layered media[J]. Computers & geosciences, 2002, 28(8): 939-950.

[6] SARAF P D, NEGI J G, ERV V. Magnetotelluric response of a laterally inhomogeneous anisotropic inclusion[J]. Physics of the earth and planetary interiors, 1986, 43(3): 196-198.

[7] PEK J, VERNER T. Finite-difference modelling of magnetotelluric fields in two-dimensional anisotropic media[J]. Geophysical Journal International, 1997, 128(3): 505-521.

[8] 霍光譜,胡祥云,黃一凡,等. 帶地形的大地電磁各向異性二維模擬及實例對比分析[J]. 地球物理學報,2015(12):4696-4708.

HUO G P, HU X Y, HUANG Y F,et al. MT modeling for 2D anisotropic conductivity structure with topography and examples of comparative analyse [J]. Chinese Journal of Geophysics,2015(12):4696-4708. ( In Chinese)

[9] REDDY I K, RANKIN D. Magnetotelluric response of laterally inhomogeneous and anisotropic media[J]. Geophysics, 1975, 40(6): 1035-1045.

[10] 徐世浙, 趙生凱. 二維各向異性地電斷面大地電磁場的有限元法解法[J]. 地震學報, 1985, 7(1): 80-89.

XU S Z, ZHAO S K. Solution of magnetotelluric field equations for a two-dimensional, anisotropic geoelectric section by the finite element method[J].Acta Seismologica Sinica, 1985, 7(1): 80-89. ( In Chinese)

[11] LI Y. A finite-element algorithm for electromagnetic induction in two-dimensional anisotropic conductivity structures[J]. Geophysical Journal International, 2002, 148(3): 389-401.

[12] 熊彬, 羅天涯, 李長偉, 等. 用有限單元法模擬各向異性介質中二維電性異常體的大地電磁響應[J]. 中山大學學報: 自然科學版, 2013, 52(4): 143-148.

XIONG B, LUO T Y, LI C W, et al. Modelling of magnetotelluric responses of 2-D electrical anomalous body in anisotropic media using finite element method[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2013, 52(4): 143-148. ( In Chinese)

[13] 羅天涯, 熊彬, 李長偉, 等. 各向異性介質中大地電磁場的異常特征[J]. 物探化探計算技術, 2013, 35(6): 645-650.

LUO T Y, XIONG B, LI C W, et al. The abnormal charcteristic of magnetotelluric in anisotrpy media [J].Computing Techniques for Geophysical and Geochemical Exploration, 2013, 35(6): 645-650. ( In Chinese)

[14] QIN L, YANG C, CHEN K. Quasi-analytic solution of 2-D magnetotelluric fields on an axially anisotropic infinite fault[J]. Geophysical Journal International, 2013, 192(1): 67-74.

[15] QIN L J, YANG C F, CHEN K. Analytic solution to the magnetotelluric response over anisotropic medium and its discussion[J]. Science China Earth Sciences, 2013, 56(9): 1607-1615.

[16] 田紅軍, 佟鐵鋼. 帶地形的二維各向異性大地電磁測深數值模擬[J]. 工程地球物理學報, 2015, 12(2): 139-144.

TIAN H J,TONG T G. The forward numerical simulation of 2D anisotropic magnetotelluric sounding[J].Chinese Journal of Engineering Geophysics,2015, 12(2): 139-144. (In Chinese)

[17] 徐世浙.地球物理中的有限單元法[M].北京：科學出版社，1994.

XU S Z. The finite element method in geophysics [M].Beijing:The Science press,1994.( In Chinese)

[18] SHEWCHUK J R. Triangle: Engineering a 2D quality mesh generator and Delaunay triangulator[C]// Selected papers from the Workshop on Applied Computational Geormetry, Towards Geometric Engineering. Springer-Verlag, 1996:203-222.

[19] REN Z, TANG J. 3D direct current resistivity modeling with unstructured mesh by adaptive finite-element method[J]. Geophysics, 2010, 75(1):H7.

[20] REN Z, KALSCHEUER T, GREENHALGH S, et al. A goal-oriented adaptive finite-element approach for plane wave 3-D electromagnetic modelling[J]. Geophysical Journal International, 2012, 194(2):700-718.

[21] 原源, 湯井田, 任政勇,等. 基于非結構化網格的任意復雜2D RMT有限元模擬[J]. 地球物理學報, 2015(12):4685-4695.

YUAN Y，TANG J T，REN Z Y，et al. Two-dimensional complicated radio-magnetotelluric finite-element modeling using unstructured grid[J]. Chinese Journal of Geophysics, 2015(12):4685-4695. ( In Chinese)

Theforwardmodelingoftwo-dimensionalanisotropicmagnetotelluricwithtopography

WANG Ning, XIAO Xiao, ZHANG Doudou

(1.Central South University School of Geosciences and Info-Physics, Changsha 410083,China;2.Central South University Key Laboratory of Metallogenic Prediction of Nonferrous Metals, Ministry of Education, Changsha 410083,China)

In the interpretation of magnetotelluric data processing, the phenomenon of anisotropy and topography are the important factors that cannot be ignored. The forward modeling of anisotropic magnetotelluric has always been the forefront subject at home and abroad. In this paper, we given the boundary value problems and its corresponding variational problem of magnetotelluric in 2D anisotropic geoelectric section from the Maxwell's equations. A triangular grid is used to discretize the calculation area, and linear interpolation is used at each triangular to compute the numerical solution with finite element method obtained the apparent resistivity and phase values. In the subsequent section we discuss the effect of the angle between the electrical spindle and Cartesian coordinate axis and topography.

magnetotelluric; FEM; anisotropic; topography

2016-10-20 改回日期： 2016-11-09

國家自然科學基金(41174105)；國家高技術研究發展計劃(2014AA06A602)

王寧(1990-)，男，碩士，主要從事電磁場理論和應用研究， E-mail：w_ning2016@163.com。

肖曉(1981-)，男，博士后，副教授，碩士生導師，主要從事電磁場理論和應用研究， E-mail：csuxiaox@csu.edu.cn。

1001-1749(2017)06-0711-08

P 631.2

A

10.3969/j.issn.1001-1749.2017.06.01