大跨度鋼桁架拱橋施工誤差敏感性分析*

康俊濤 胡 杰 董培東 邢英興曹宏猷 孫雪平 秦世強 邵光強

(武漢理工大學土木工程與建筑學院1) 武漢 430070) (中交武漢港灣工程設計研究院有限公司2) 武漢 430000)

大跨度鋼桁架拱橋施工誤差敏感性分析*

康俊濤1)胡 杰1)董培東1)邢英興2)曹宏猷1)孫雪平1)秦世強1)邵光強1)

(武漢理工大學土木工程與建筑學院1)武漢 430070) (中交武漢港灣工程設計研究院有限公司2)武漢 430000)

為研究大跨度鋼桁架拱橋的拱肋線形對施工誤差的敏感性，以蘇嶺山大橋主橋為例，以設計理想狀態的有限元模型為基準，研究了結構自重、剛度、溫度、節段角度誤差對拱肋最大懸臂狀態、合龍狀態、成橋狀態的拱肋線形的影響.結果表明，這三種狀態下的拱肋不同截面累積撓度均對同種類型施工誤差的敏感性不同；這三種狀態下的拱肋線形均對拼裝角度最敏感，對結構自重和溫度比較敏感，對結構剛度敏感性較低；在不同狀態下，對施工誤差最敏感的主要截面位置不同；并針對該類橋梁的施工特點，提出誤差識別和拱肋線形控制的建議.

鋼桁架拱橋；拱肋線形；施工誤差；敏感性

0 引 言

鋼桁架拱橋具有外形美觀、跨越能力大、承載能力高、耐久性能好等優點[1]，在大跨徑橋梁選型中具有較強的競爭力.

許多學者對此類問題進行了研究，郭玉龍[2]的研究表明,拱肋桁架的節點板、高強螺栓和橫隔板質量占拱肋總質量的10%以上，且對施工階段的桿件應力影響顯著.由文獻[3]可知，節點剛域效應對懸臂拼裝的鋼桁架連續梁橋施工過程中的桿件應力影響明顯.魏群[4]研究了節點剛度對壩陵河大橋成橋狀態構件力學特性的影響，表明節點剛度會導致鋼桁架加勁梁整體剛度增大，桿件應力分布差別明顯.鋼桁架的加工、制作和安裝溫度一般存在地域差異和季節差異，所處環境溫差大，且與設計基準溫度差別較大.拱肋拼裝角度誤差對榕江特大橋拱肋線形的影響較大，線形偏差基本來源于角度誤差[5].盧偉升[6]對拱肋多種典型的施工標高誤差進行了結構的成橋受力影響分析，得出不同的施工標高誤差類型對結構的成橋受力影響差別很大.吳海軍[7]研究了鋼-混凝土組合拱橋豎轉施工中的合龍誤差對箱形鋼拱肋受力情況的影響，為同類橋梁的強迫合龍提供了理論依據.

目前，對于鋼桁架拱橋施工誤差的研究集中在施工過程中的結構受力情況，而對施工過程中不同狀態下的拱肋線形對不同施工誤差的敏感程度研究較少.文中擬以蘇嶺山大橋主橋設計理想狀態有限元模型為基準，研究結構自重、剛度、溫度和節段拼裝角度誤差對拱肋最大懸臂狀態、拱肋合龍狀態及成橋狀態下的拱肋線形的影響，對比確定不同狀態下的拱肋線形對不同施工誤差的敏感程度.

1 工程概況及計算模型

1.1 工程概況

蘇嶺山大橋主橋為三跨下承式連續鋼桁架拱橋，跨徑組合為70 m+240 m+70 m，全長為380 m，橋面全寬為43.9 m，見圖1.

圖1 蘇嶺山大橋主橋(單位：cm)

拱肋由兩片N桁架和八道空間桁架式一字風撐組成，兩片拱肋桁架橫向中心間距38.2 m.N桁架由上弦桿、下弦桿和腹桿組成，上、下弦桿采用高強螺栓連接的箱形截面，上弦桿采用二次拋物線和圓曲線相結合，下弦桿采用拋物線，矢高54 m，矢跨比1/4.444，中跨腹桿采用工字形截面，邊跨腹桿采用1.498 m×0.8 m的箱形截面.風撐弦桿采用平行四邊形箱形截面，豎腹桿、平聯桿均采用H形截面.橋面主縱梁內寬1.5 m，豎向中心線處全高2.7 m.縱梁間設置鋼橫梁，鋼橫梁上翼緣設雙向2%橫坡，橋梁中心線處腹板高3.054 m，橫梁分工字形截面和箱形截面.主墩采用直徑4 m的實心圓形墩，兩墩柱之間設直徑3.2 m的實心方形系梁；邊墩為直徑2 m的四柱實心圓形墩.

蘇嶺山大橋主橋主要施工流程如下：①在兩岸臨時支撐平臺上拼裝邊跨拱肋和邊跨橫梁；②安裝塔架和纜索系統并懸臂拼裝主跨拱肋；③張拉后錨索和前扣索并懸臂拼裝剩余主跨拱肋直至拱肋合龍；④安裝并張拉臨時系桿，吊裝主跨橋面梁節段直至主梁合龍；⑤二次張拉吊桿，調整主梁線形；⑥解除錨扣系統和臨時系桿，安裝橋面系及附屬構件.

1.2 計算模型

采用有限元分析軟件MIDAS Civil 2015建立設計理想狀態有限元模型，見圖2.

圖2 設計理想狀態有限元模型

模型中拱肋、主縱梁、橫梁、扣塔采用梁單元模擬，扣索、臨時系桿、吊桿采用桁架單元模擬.全橋共劃分為3 736個單元，2 673個節點，各主要構件材料特性見表1.施工過程模擬按設計圖紙考慮的臨時荷載包括邊跨臨時壓重、扣塔自重和扣索索力等.邊跨壓重、防撞欄桿、橋面鋪裝荷載均按均布荷載考慮.拱肋最大懸臂狀態和合龍狀態：中支座固定，邊支座縱向活動；成橋狀態：一中支座固定，其余支座縱向活動.

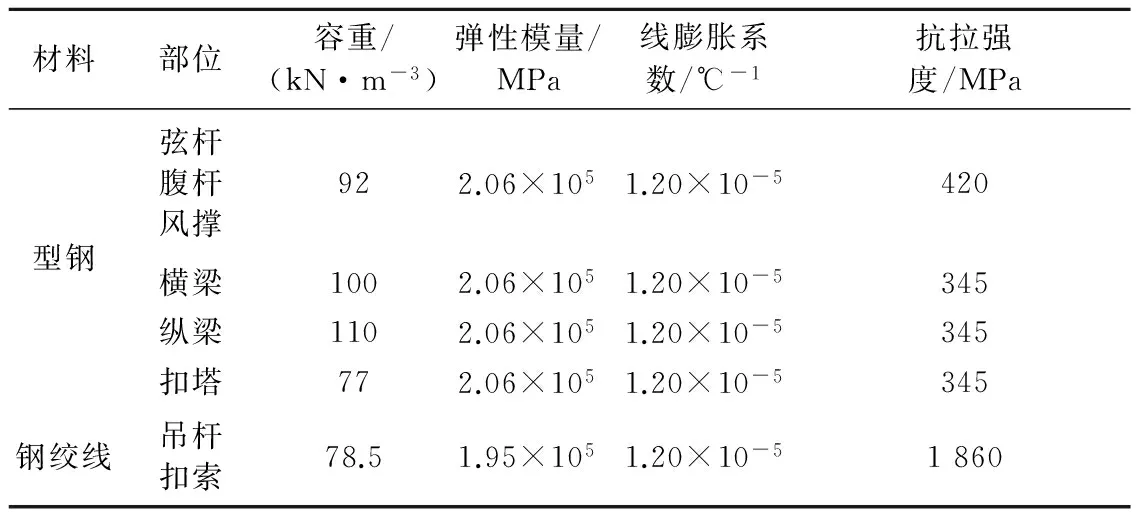
表1 主要構件材料特性表

2 控制指標的確定

鋼桁架拱橋的線形、應力對于施工質量和結構安全至關重要，但目前應力測量精度不夠，實測值波動較大，而線形測量精度較高，現場操作方便快捷.柳鑫星[8]對之江大橋線形控制技術的研究表明，對大跨度鋼橋的施工進行線形控制，施工誤差小，能保證成橋線形滿足設計和規范要求.王虎勝[9]采用線形控制方法對某大跨度剛構橋的合龍方案進行了對比分析，為該類橋梁的合龍方案選擇提供了寶貴建議.王海峰[10]的研究結果表明，在大跨度橋梁的懸臂澆筑施工中，保持主梁線形在控制范圍內是確保結構受力安全的一個重要手段.因而，選取各控制截面的累積撓度作為誤差敏感性分析的控制指標.

以蘇嶺山大橋主橋設計理想狀態有限元模型為基準，分析結構自重、剛度、溫度和節段拼裝角度誤差按不同倍數變化對拱肋最大懸臂狀態、拱肋合龍狀態和成橋狀態的拱肋線形的影響，以便與大橋施工過程中的拱肋實測線形進行對比，對實際施工誤差的類型和大小進行識別，進而為拱肋線形的調整和控制提供參考.其中，結構自重按照1.03，1.06，1.09，1.12的倍數變化，自重的調整通過改變材料的容重實現；結構剛度按1.03，1.06，1.09，1.12的倍數變化，剛度的調整通過改變材料的彈模實現；結構溫度按照-20，-10，10，20 ℃變化，溫度的調整通過系統升降溫實現；節段拼裝角度誤差Δθ按照-0.002，-0.001，0.001，0.002 rad變化，角度誤差的調整通過使懸拼節段繞前一節段上弦桿拼接點整體旋轉相應角度實現，節段整體向上轉動為正，向下轉動為負.

3 施工誤差敏感性分析

3.1 拱肋最大懸臂狀態

結構自重、剛度、溫度和拼裝角度變化時，拱肋最大懸臂狀態下的拱肋各控制截面累積撓度與設計理想狀態的比較結果見圖3.圖中正值撓度表示拱肋上抬，負值撓度表示拱肋下撓.

圖3 四種因素對最大懸臂狀態主拱線形的影響

由圖3可知：①隨著結構自重的增大，拱腳處截面下撓4%～17%，(1/8)L處截面下撓23%～91%，(1/4)L處截面下撓23%～93%，(3/8)L處截面下撓26%～102%.②隨著結構剛度的增大，拱腳處截面上抬3%～10%，(1/8)L處截面下撓6%～23%，(1/4)L處截面下撓7%～24%，(3/8)L處截面下撓7%～25%.③隨著結構溫度的變化，拱腳處截面累積撓度變化3%～6%，(1/8)L處截面累積撓度變化40%～81%，(1/4)L處截面累積撓度變化23%～45%，(3/8)L處截面累積撓度變化18%～35%.④隨著拼裝角度的變化，拱腳處截面累積撓度變化8.10～16.19倍，(1/8)L處截面累積撓度變化4.68～9.36倍，(1/4)L處截面累積撓度變化2.29～4.58倍，(3/8)L處截面累積撓度變化1.59～3.18倍.

由上述控制截面撓度變化可得：

1) 拱肋最大懸臂狀態下的拱肋線形對不同類型施工誤差的敏感性差別很大.其中，拱肋線形對拼裝角度最敏感，累積撓度變化最大為16.19倍；對結構自重很敏感，累積撓度變化最大為102%；對結構溫度比較敏感，累積撓度變化最大為81%；對結構剛度的敏感性較低，累積撓度變化最大為25%.

2) 拱肋最大懸臂狀態下的拱肋不同截面累積撓度對同種類型施工誤差的敏感性不同.結構自重增大，各控制截面累積撓度變化最大值為17%～102%；結構剛度增大，各控制截面累積撓度變化最大值為10%～25%；結構溫度變化，各控制截面累積撓度變化最大值為6%和81%之間；拼裝角度變化，各控制截面累積撓度變化最大值為3.18～16.19倍.

3) 在拱肋最大懸臂狀態下，對不同類型施工誤差最敏感的截面位置主要為(3/8)L處.結構自重增大，累積撓度變化最大的截面為(3/8)L處截面；結構剛度增大，累積撓度變化最大的截面為(3/8)L處截面；結構溫度變化，累積撓度變化最大的截面為(1/8)L處截面；拼裝角度變化，累積撓度變化最大的截面為拱腳處截面.

3.2 拱肋合龍狀態

結構自重、剛度、溫度和拼裝角度變化時，拱肋合龍狀態下的拱肋各控制截面累積撓度與設計理想狀態的比較結果見圖4.

圖4 四種因素對拱肋合龍狀態主拱線形的影響

由圖4可知：①隨著結構自重的增大，拱腳處截面下撓4%～17%，(1/8)L處截面下撓21%～85%，(1/4)L處截面下撓23%～92%，(3/8)L處截面下撓27%～107%，(1/2)L處截面下撓29%～118%.②隨著結構剛度的增大，拱腳處截面上抬3%～10%，(1/8)L處截面下撓6%～22%，(1/4)L處截面下撓7%～24%，(3/8)L處截面下撓7%～26%，(1/2)L處截面下撓8%～27%.③隨著結構溫度的變化，拱腳處截面累積撓度變化11%～23%，(1/8)L處截面累積撓度變化41%～82%，(1/4)L處截面累積撓度變化54%～108%，(3/8)L處截面累積撓度變化57%～114%，(1/2)L處截面累積撓度變化42%～83%.④隨著拼裝角度的變化，拱腳處截面累積撓度變化8.22～16.44倍，(1/8)L處截面累積撓度變化4.39～8.78倍，(1/4)L處截面累積撓度變化2.27～4.54倍，(3/8)L處截面累積撓度變化1.67～3.34倍，(1/2)L處截面累積撓度變化1.36～2.55倍.

由上述控制截面撓度變化可得：

1) 拱肋合龍狀態下的拱肋線形對不同類型施工誤差的敏感性差別很大：對拼裝角度最敏感，累積撓度變化最大為16.44倍；對結構自重和溫度很敏感，累積撓度變化最大分別為118%和114%；對結構剛度的敏感性較低，累積撓度變化最大為27%.

2) 拱肋合龍狀態下的拱肋不同截面累積撓度對同種類型施工誤差的敏感性不同.結構自重增大，各控制截面累積撓度變化最大值為17%～118%；結構剛度增大，各控制截面累積撓度變化最大值為10%～27%；結構溫度變化，各控制截面累積撓度變化最大值為23%～83%；拼裝角度變化，各控制截面累積撓度變化最大值為2.55～16.44倍.

3) 在拱肋合龍狀態下，對不同類型施工誤差最敏感的截面位置主要為(1/2)L處.結構自重增大，累積撓度變化最大的截面為(1/2)L處截面；結構剛度增大，累積撓度變化最大的截面為(1/2)L處截面；結構溫度變化，累積撓度變化最大的截面為(3/8)L處截面；拼裝角度變化，累積撓度變化最大的截面為拱腳處截面.

3.3 成橋狀態

結構自重、剛度、溫度和拼裝角度誤差變化時，成橋狀態下的拱肋各控制截面累積撓度與設計理想狀態的比較結果見圖5.

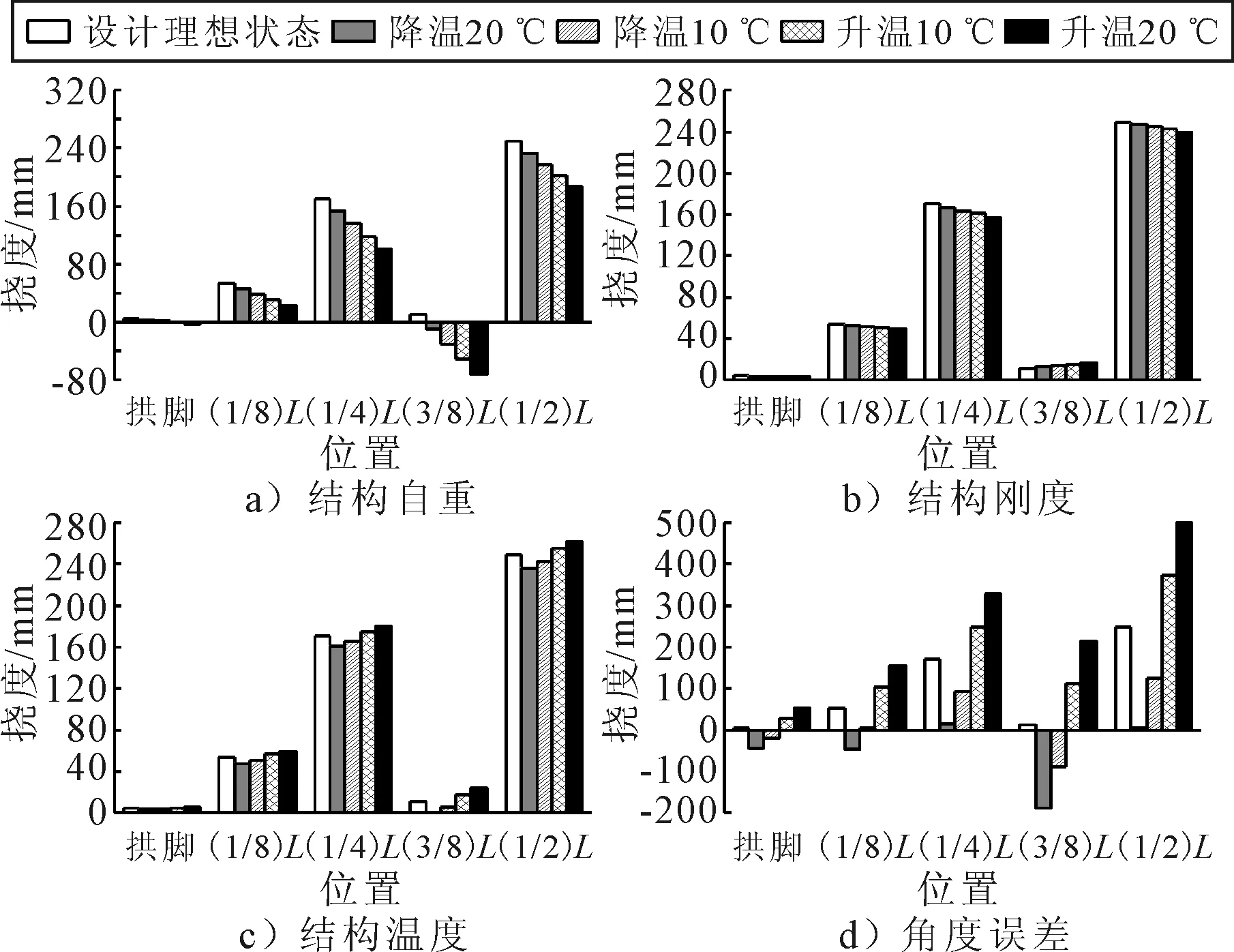
圖5 四種因素對成橋狀態主拱線形的影響

由圖5可知：①隨著結構自重的增大，拱腳處截面下撓38%～153%，(1/8)L處截面下撓14%～58%，(1/4)L處截面下10%～40%，(3/8)L處截面下撓1.84～7.37倍，(1/2)L處截面下撓6%～25%.②隨著結構剛度的增大，拱腳處截面下撓5%～18%；(1/8)L處截面下撓2%～7%；(1/4)L處截面下撓2%～8%；(3/8)L處截面下撓14%～47%；(1/2)L處截面下撓1%～4%.③隨著結構溫度的變化，拱腳處截面累積撓度變化10%～19%；1/8L處截面累積撓度變化5%～11%；(1/4)L處截面累積撓度變化3%～6%；(3/8)L處截面累積撓度變化54%～108%；(1/2)L處截面累積撓度變化3%～5%.④隨著拼裝角度的變化，拱腳處截面累積撓度變化5.57～11.14倍；(1/8)L處截面累積撓度變化0.93～1.88倍；(1/4)L處截面累積撓度變化0.46～0.93倍；(3/8)L處截面累積撓度變化8.88～17.77倍；(1/2)L處截面累積撓度變化0.50～1.00倍.

由上述控制截面撓度變化可得：

1) 成橋狀態下的拱肋線形對不同類型施工誤差的敏感性差別很大：對拼裝角度最敏感，累積撓度變化最大為17.77倍；對結構自重很敏感，累積撓度變化最大為7.37倍；對結構溫度較敏感，累積撓度變化最大為108%；對結構剛度的敏感性較低，累積撓度變化最大為47%.

2) 成橋狀態的拱肋不同截面累積撓度對同種類型施工誤差的敏感性不同.結構自重增大，各控制截面累積撓度變化最大值為25%～7.37倍；結構剛度增大，各控制截面累積撓度變化最大值為4%～47%；結構溫度變化，各控制截面累積撓度變化最大值為5%～108%；拼裝角度變化，各控制截面累積撓度變化最大值為1倍～17.77倍.

3) 在成橋狀態下，施工誤差類型不同，累積撓度變化最大的截面位置均為(3/8)L處，最敏感的截面位置相同.

4 結 論

1) 這三種狀態下的拱肋不同截面累積撓度均對同種類型施工誤差的敏感性不同.建議在施工誤差識別中，應根據需識別的誤差類型，選擇對該種誤差最敏感的控制截面進行觀測，以便在提高誤差識別精度的同時，合理減少測量工作量.

2) 在不同狀態下，對施工誤差最敏感的主要截面位置不同.最大懸臂狀態下最敏感的截面位置主要在(3/8)L處，合龍狀態下最敏感的截面位置主要在(1/2)L處，成橋狀態下最敏感的截面位置均在(3/8)L處.建議在拱肋懸臂狀態下應加強對(3/8)L處截面累積撓度的關注，通過(3/8)L處截面的累積撓度與設計理想狀態模型計算結果的對比，對施工誤差的大小進行識別.另外，可通過控制(3/8)L處截面的累積撓度滿足設計和規范要求的方法對整個拱肋線形進行控制.

3) 這三種狀態下的拱肋線形均對拼裝角度最敏感，對結構自重和溫度比較敏感，對結構剛度敏感性較低.建議將施工誤差控制的重點放在拼裝角度上，加大力度提高節段拼裝角度的精確程度，并在下一節段拼裝前，仔細核對已拼前一節段的空間坐標，若拼裝角度存在誤差及時采取糾偏措施.在最大懸臂狀態，應對全天溫度和相應溫度下的拱肋線形進行跟蹤測量，確定拱肋線形與環境溫度的對應關系，選擇合適的環境溫度進行拱肋合龍施工，盡量減小合龍口誤差，實現拱肋的無應力合龍.

[1] 孫海濤.大跨度鋼桁架拱橋控制問題研究[D].上海:同濟大學，2006.

[2] 郭玉龍.大跨度鋼桁架拱橋施工控制技術研究[D].成都:西南交通大學，2015.

[3] 張永健.節點剛域效應對斜拉式桁架橋的受力影響[J].長安大學學報(自然科學版)，2007,27(2):42-45.

[4] 魏群.大型鋼桁架懸索橋節點剛度對成橋受力影響探討[J].公路，2009(3):29-33.

[5] 蔡祿榮.大跨度鋼桁架拱橋預拱度設置及拼裝誤差理論研究[D].廣州：華南理工大學，2012.

[6] 盧偉升.大跨度鋼管混凝土拱橋拱肋施工誤差影響分析[J].中外公路，2015,35(3):84-88.

[7] 吳海軍.鋼-混凝土組合拱橋豎轉施工誤差分析[J].重慶交通大學學報(自然科學版)，2010,29(1):4-7.

[8] 柳鑫星.拱形鋼塔斜拉橋線形控制技術[J].公路，2013(4):36-39.

[9] 王虎勝.基于線形控制的山區大跨度剛構橋合龍方案對比研究[J].公路，2016(7):100-103.

[10] 王海峰.懸臂澆筑預應力混凝土箱梁線形控制技術[J].公路，2010(9):117-119.

Sensitivity Analysis on Construction Error of Long-span Steel Trussed Arch Bridge

KANGJuntao1)HUJie1)DONGPeidong1)XINGYingxing2)CAOHongyou1)SUNXueping1)QINShiqiang1)SHAOGuangqiang1)

(SchoolofCivilEngineeringandArchitecture,WuhanUniversityofTechnology,Wuhan430070,China)1)(ChineseShippingWuhanHarborEngineeringDesign&ResearchInstituteCo.,Wuhan430000,China)2)

The sensitivity of construction error on the linearity of arch ribs for long-span steel trussed arch bridges is analyzed in this paper. Taking the Suling Mountain bridge as an example,the finite element model of the ideal state is used as the benchmark. The influences of self-weight,stiffness,temperature and segment angle errors on arch rib alignment are analyzed under the maximum cantilever state,the closed-loop state and the finished state of arch ribs. The results show that the sensitivity of cumulative deflections of arch ribs with different cross-sections in the three states is different for the same type of construction error. The linearity of arch ribs in these three states is most sensitive to the assembling angle,sensitive to the structure weight and temperature, but low to the structural stiffness. In the different states,the main cross-sectional positions most sensitive to construction errors are different. The paper also puts forward the suggestions of error identification and linear control of arch ribs according to the construction characteristics of this kind of bridge.

steel truss arch bridge; linearity of arch rib; construction error; sensitivity

U448.211

10.3963/j.issn.2095-3844.2017.06.002

2017-09-17

康俊濤(1978—)：男，博士，教授，主要研究領域為橋梁工程

*國家自然科學基金項目(51408449)、湖北省自然科學基金項目(2015CFB393)資助