基于頻域相關性判決的壓制干擾分類識別?

白 杰 楊 林 孫殿星 張翔宇

（海軍航空工程學院信息融合研究所 煙臺 264001）

基于頻域相關性判決的壓制干擾分類識別?

白 杰 楊 林 孫殿星 張翔宇

（海軍航空工程學院信息融合研究所 煙臺 264001）

針對有源壓制干擾的分類識別問題，提出了一種基于功率譜相關性判決的分類識別算法。首先對不同有源壓制干擾類型進行建模，并著重對干擾信號的功率譜特性進行分析；然后，針對不同壓制干擾類型在功率譜分形特性中表現出來的特征差異，通過求取與白噪聲的功率譜相關系數將分形特性進行量化，來反映不同干擾類型之間的差異程度；最后，通過建立相關系數門限完成壓制干擾的分類識別。仿真結果表明，論文算法具有較高的分類識別正確率，并且與現有壓制干擾分類識別算法相比，實時性更強。

有源壓制干擾；相關性系數；門限判決；分類識別

1 引言

現代雷達所面臨的電磁環境日益惡劣，針對雷達的電磁干擾技術迅速發展，其中有源壓制干擾的大量使用，極大制約了雷達作戰效能的發揮［1］。面對有源壓制干擾，對干擾信號的分類識別成為抗干擾工作的關鍵，根據干擾信號的分類識別結果，抗干擾系統才能有針對性的采取抗干擾措施，因此，對有源壓制干擾的快速分類識別是當前抗干擾領域急需解決的一個關鍵問題。

目前，國內外學者在壓制干擾分類識別方面做了大量研究，文獻［2］提出了一種基于隨機投影和稀疏分類的雷達波形識別算法；文獻［3～4］分別提取不同的時域特征參數對有源壓制干擾進行分類識別；文獻［5］提取信號的一階矩和二階矩作為特征參數，并通過分類器實現有源壓制干擾的分類識別；文獻［6］將回波信號轉換為時頻圖像，并利用前饋神經網絡實現壓制干擾的分類識別；文獻［7］提取信號在FRFT域的信息維度和盒維數作為特征參數，通過門限判決法完成干擾類型的分類識別。從仿真結果可以看出，上述文獻算法均能達到較高的分類識別正確率，但普遍存在特征參數提取復雜，計算量較大，實時性較差的問題。

針對這一問題，本文充分分析了射頻噪聲干擾、噪聲調幅干擾和噪聲調頻干擾三種常規壓制干擾在功率譜特性上的差異，提出了一種基于頻域相關性判決的壓制干擾分類識別算法。

2 壓制干擾建模與特性分析

1）射頻噪聲干擾JRF(t)的時域表達式為［8］

其中，包絡函數Uj(t)服從瑞利分布，?(t)為相位函數，ωj表示中頻窄帶噪聲的中心頻率，且遠大于J(t)的譜寬。射頻噪聲干擾產生原理簡單，能夠對雷達形成遮蓋式干擾效果。假定射頻噪聲的有效帶寬為Δf，σ2為射頻噪聲在接收機輸入端的功率，中心頻率為 fj，則射頻噪聲干擾的功率譜表示為

由式（1）可以看出，射頻噪聲干擾在有限頻帶范圍內具有均勻的功率譜密度。

2）噪聲調幅干擾JAM(t)的時域表達式為［9］

其中，U0為直流偏置，un(t)為調制噪聲，φ為調幅干擾初始相位。噪聲調幅干擾的干擾功率集中在以載頻為中心的較窄帶寬范圍內，常應用于窄帶瞄準式干擾。設噪聲調幅干擾的載頻為 fj，調制噪聲功率譜為Sn(f)，則噪聲調幅干擾的功率譜表示為

由式（4）可以看出，噪聲調幅干擾的功率為載波功率加上調制噪聲功率的一半，并且，在不產生過調制條件下，調制噪聲功率只占調幅干擾功率很小的一部分，所以，噪聲調幅干擾的功率譜脈沖特性明顯。

3）噪聲調頻干擾是目前應用最廣泛的一種壓制干擾形式，噪聲調頻干擾具有較寬的干擾帶寬和較大的干擾功率，且干擾帶寬可調，能夠適用于多種干擾的需求。噪聲調頻干擾JFM(t)時域表達式為［10］

其中，u(t)與ψ(t)分別對應調頻信號的瞬時頻率及瞬時相位，γ為初始相位，Uj為噪聲調頻信號的幅度，ωj為噪聲調頻信號的中心頻率，KFM為調頻斜率。定義mfe=KFM×σ Ωn為有效調頻指數，Ωn為調制噪聲帶寬，σ2為調制噪聲方差，KFM為調制斜率。當mfe≥1時，其功率譜離散形式表示為

由式（6）可以看出，噪聲調頻干擾的功率譜既不像射頻噪聲干擾那樣較均勻分布，也不像噪聲調幅干擾那樣脈沖特性明顯，而是介于兩者之間，服從一定的分布規律。

通過以上對三種壓制干擾功率譜特性的分析可以看出，三種壓制干擾在功率譜分布上表現出較明顯差異，根據功率譜特征差異，提取功率譜分形特性作為特征參數，作為壓制干擾分類識別的依據。

3 壓制干擾分類識別算法

3.1 基于相似性理論的特征參數分析

結合信號相似性理論［11～12］對不同壓制干擾的分形特性進行分析。

假定兩個能量有限的確定信號分別為x(t)、y(t)，選擇適當的參數c使得cy(t)去逼近x(t)。利用均方誤差，即能量誤差ε2說明兩者之間的相似程度：

上式對c求導并領結果等于0，即

當c滿足下式時，將使ε2最小，即誤差能量最小，cy(t)最接近于x(t)：

ρxy從信號之間能量誤差的角度描述了他們的相關特性，利用矢量空間的內積運算也可以給出定量說明。當相關系數 ρxy=1時，誤差能量0，說明兩個信號相似度很好，是線性相關的；當 ρxy=0時，相似度最差即不相關。因此把相關系數作為兩個信號波形的相似性（或線性相關性）的一種度量是合理的。對于離散信號，相關系數的離散公式［13］表示為

圖1和圖2分別表示一組波形相關的信號和一組波形不相關的信號，根據式（11）可得，圖1中兩信號的相關系數為0.82，圖2中兩信號的相關系數為0.13。可見，信號相似性理論可以有效地判別兩個信號的相似程度。

根據不同壓制干擾的功率譜分布差異，通過求取與白噪聲的功率譜相關系數將差異進行量化，并進一步進行分類識別。

設回波信號的功率譜為Sx(k)(k=1，2，…，N)，白噪聲的功率譜為Sn(k)，對回波信號和白噪聲信號進行功率歸一化處理，即(k)=1，(k)=1。由于白噪聲在各頻率點的功率相同，所以近似有S(k)=，(n=1……N ) ，則式（11）可以簡化為

3.2 壓制干擾分類識別算法

結合實際情況，做出如下假設：接收機為理想帶寬接收機，其幅頻特性為固定值，相頻為線性，而在通帶之外的增益為零，背景噪聲為高斯白噪聲，且三種壓制干擾均能夠實現接收機頻帶覆蓋。

由式（8）可以看出相關系數 ρxn與()k成反比關系。對于()

k，由基本不等式公式可知，Sx()k(

)

結合三種壓制干擾的功率譜分布特性：射頻噪聲干擾的功率譜近似均勻分布；噪聲調幅干擾的功率譜類似于脈沖信號；噪聲調頻干擾功率譜特性介于兩者之間，所以，射頻噪聲干擾與白噪聲的功率譜相關系數最大；噪聲調幅干擾與白噪聲的功率譜相關系數最小；噪聲調頻干擾與白噪聲的功率譜相關系數介于兩者之間。

根據以上分析建立相關性判決門限分別為η1和η2，根據ρxn與門限的大小關系進行如下判決：

4 仿真分析與驗證

4.1 仿真參數設置

取過程噪聲為高斯白噪聲，門限判決算法中，門限值η1和η2分別為0.35和0.85。

表1 干擾信號仿真參數表

4.2 仿真實驗驗證

1）三種常規壓制干擾的時域波形與功率譜如圖4所示。

圖4（a）、圖4（b）、圖4（c）分別表示射頻噪聲干擾、噪聲調頻幅干擾和噪聲調頻干擾的時域波形和功率譜。由三種干擾的功率譜可以看出，三種干擾的功率譜特性差異明顯：射頻噪聲干擾在各個頻點處的功率譜值近似相等，噪聲調幅干擾的功率集中在載頻處，而射頻噪聲干擾的功率譜特性介于兩者之間。三種干擾功率譜之間的特性差異為三種干擾的分類識別提供了很好的依據。

2）三種壓制干擾與白噪聲功率譜的相關系數仿真如圖5所示。

圖5（a）表示射頻噪聲干擾與白噪聲的功率譜相關系數，由于射頻噪聲干擾是由白噪聲通過窄帶濾波器產生的，所以相關系數受JNR的影響很小，且兩者相關性較強。

圖5（b）表示不同峰值系數下噪聲調幅干擾與白噪聲的功率譜相關系數，由圖可以看出，當JNR較大時，相關系數趨于穩定，并且兩者的相關性較弱。

圖5（c）表示不同調制系數下噪聲調頻干擾與白噪聲的功率譜相關系數，由圖可以看出，在不同參數條件下相關系數的差異較大。

通過對比可以得出結論：三種壓制干擾與白噪聲的功率譜相關系數差異較為明顯，可以作為區分三種壓制干擾類型的依據。

3）本文算法與文獻［14］算法的分類識別結果對比如圖6所示。

通過對比可以看出，當JNR大于10dB后，兩種算法均能達到較高的分類識別正確率；當JNR在5dB與10dB之間時，本文算法優于文獻［14］算法；當JNR小于5dB時，本文算法對射頻噪聲干擾的正確識別率優于文獻［14］算法，對噪聲調幅干擾以及噪聲調頻干擾的正確率略差于文獻［14］算法。

4）分別進行50次蒙特卡洛仿真實驗，本文算法和文獻［14］算法在耗時上的對比如表2所示。

通過表2可以看出，相比于文獻［14］算法，本文算法在特征參數提取以及分類識別方面的耗時大大縮短，所以算法實時性更強。

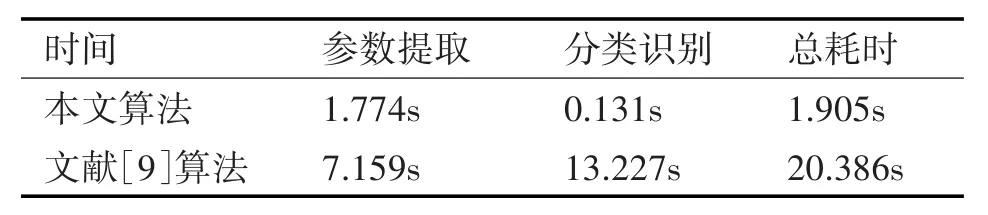
表2 仿真實驗耗時對比

5 結語

本文對有源壓制干擾的分類識別問題進行了研究，在充分分析不同壓制干擾類型功率譜特性的基礎上，通過求取與白噪聲的功率譜相關系數，將功率譜的分形特性進行量化，并最終通過門限判別的方法進行干擾分類識別。與現有算法相比，本文算法在保證分類識別正確率的前提下，算法耗時更短，實時性更強。

［1］趙國慶.雷達對抗原理（第二版）［M］.西安：西安電子科技大學出版社，2012.

［2］Ma J，Huang G，Zuo W，et al.Robust radar waveform rec?ognition algorithm based on random projections and sparse classification［J］.Radar Sonar&Navigation Iet，2014，8（4）：290-296.

［3］Tang Zhu，Zhang Bing，Li Guangqiang.Radar active blan?ket jamming sorting based on resemblance coefficient cluster［C］//IEEE International Conference on Signal Pro?cessing，2013：1-6.

［4］杜東平.雷達壓制式干擾抑制算法研究［D］.成都：電子科技大學，2008：11-21.

［5］Du D P.Research on Radar Suppress Interference Sup?pression Algorithm［D］.Chengdu：University of Electronic Science and Technology，2008：11-21.

［6］Lu L，Yang J，Wang H，et al.The analysis and feature ex?traction of nonstationary random characteristics of radar jammer signal［C］//International Symposium on Electro?magnetic Compatibility.IEEE，2002：660-663.

［6］Haykin S，Bhattacharya T K.Modular learning strategy for signal detection in a nonstationary environment［C］//MIL?COM 97 Proceedings.IEEE，1997：1113-1116 vol.3.

［7］Zhu Hong，Jiang Ge，Zhang Hai.Existence detection of blanket jamming based on fractal characteristics in FRFT domain［J］.強激光與粒子束，2016，28（5）：1-7.

［8］Ticconi F，Anderson C，Figa-Saldana J，et al.Analysis of Radio Frequency Interference in Metop ASCAT Back?scatter Measurements［J］.IEEE J-STARS，2017，PP（99）：1-12.

［9］Xiang L，Ding J，Lv J.Research on dynamic evaluation of anti-complex blanketing jamming capability of netted ra?dar system［C］//International Conference on Industrial and Information Systems.IEEE，2010：265-268.

［10］Prosenjit Bhattacharyy，Santosh Kumar Dawn ；Tara?prasad Chattopadhyay.Performance of a band reject tun?able microwave filter in the face of frequency-modulated interference［C］//Bombay Section Symposium（IBSS），2015 IEEE

［11］Azuelosatias S.Identifying the meanings hidden in legal texts：The three conditions of relevance theory and their sufficiency［J］.Semiotica，2016，2016（209）：99-123.

［12］Juan Liu，Huijuan Jia.The Study of Verbal Allusion Translation in Film Subtitle：Based on Relevance Theory［J］.Theory and Practice in Language Studies，2014，4（1）：112-116.

［13］Xu W，Ma R，Zhou Y，et al.Asymptotic properties of Pearson's rank-variate correlation coefficient in bivariate normal model［J］.Signal Processing，2016，119（C）：190-202.

［14］唐翥，張兵，李廣強，等.基于特征加權與SVM的雷達有源干擾分類技術［J］.火力與指揮控制，2014，39（5）：114-116.

Classification of Compression Interference Based on Frequency Domain Correlation Judgment

BAI JieYANG Lin SUN DianxingZHANG Xiangyu
（Institute of Information Fusion，Naval Aeronautical and Astronautical University，Yantai 264001）

Aiming at the problem of classification and recognition of active suppression interference，a classification recogni?tion algorithm based on power spectrum correlation decision is proposed.Firstly，the different types of active suppression disturbanc?es are modeled and the power spectrum characteristics of the jamming signals are analyzed.Then，according to the different charac?teristics of the different types of noise suppression in the fractal characteristics of the power spectrum，The power spectral correla?tion coefficient is used to quantify the fractal characteristics to reflect the degree of difference between different interference types.Finally，the classification and recognition of the suppression interference is accomplished by establishing the correlation coefficient threshold.The simulation results show that the algorithm has high accuracy of classification and recognition，and it is more re?al-time than the existing suppression interference classification and recognition algorithm.

active suppression interference，correlation coefficient，threshold decision，classification recognition

TN954+.1

10.3969/j.issn.1672-9730.2017.11.009

Class Number TN954+.1

2017年5月4日，

2017年6月25日

國家自然科學基金（編號：61372027；61671462；61501489）；泰山學者攀登計劃資助。

白杰，男，碩士研究生，研究方向：雷達抗干擾。楊林，男，碩士研究生，研究方向：雷達抗干擾。孫殿星，男，博士研究生，助理工程師，講師，研究方向：數據融合。張翔宇，男，博士研究生，助理工程師，講師，研究方向：數據融合。