利用小波能量特征的增長型自組織神經網絡同調機組分群方法*

楊越，王濤，顧雪平，岳賢龍，徐振華，邱麗君

（1.華北電力大學新能源電力系統國家重點實驗室，河北保定071003；2.國網福建省電力有限公司電力科學研究院，福州350007；3.中國電力科學研究院，北京100192）

0 引 言

電力系統中發電機功角不是一成不變的，而是隨著外界擾動和運行狀態的變化而變化，發電機功角在變化過程中，不同的機組可能具有一致的動態變化特性，即機組之間存在著同調現象［1］。可以依據電力系統中機組之間的同調性將整個系統分成各個互相解耦的子系統，進而簡化系統模型。比如：當系統發生低頻振蕩時，若存在著弱互聯區域，通常應用機組之間的同調現象將系統分區域研究［2］；在EEAC法中，也是先進行發電機的兩群假設，將發電機分為臨界機群和剩余機群［3］。除此之外，當電網受到大沖擊，為了避免發生連鎖故障［4］、防止大停電而進行的解列控制［5］也多以同調機組分群為基礎。所以精準識別電力系統的同調特性具有重要意義。

目前，機組分群方法主要有兩類，第一類是建立系統發電機模型，然后選出一個反映系統發電機同調性的參數，根據參數的相似程度進行分群；第二類是仿真擾動后發電機功角的變化趨勢，通過辨識功角搖擺曲線相似程度進行同調分群。其中第二種方法應用越來越廣泛，很多學者采用時域分析、頻域分析、時頻分析來確定發電機功角搖擺曲線的相近程度。時域分析方法主要包括提取時域特征［6］、曲線相關分析［7］等。為了獲得更精確的反映發電機功角搖擺曲線趨勢的特征，一些學者利用頻域分析方法，采用傅里葉變換來提取頻譜分布特征［8］。時域分析能夠提取分辨率很高的時域特征，但是頻域分辨率卻很低，頻域分析能夠提取分辨率很高的頻域特征，但是時域分辨率卻很低，都不能全面準確提取功角搖擺曲線的特征。為此，很多學者利用時頻分析來提取功角搖擺曲線特征，小波變換就是其中的典型代表。小波變換結合了時域分析和頻域分析的優勢，在高頻部分具有很高的時間分辨率，在低頻部分具有很高的頻率分辨率，提取的特征能夠全面準確地反映功角搖擺曲線特性［9］。文獻［10］采用小波分解方法將功角搖擺曲線分解為高頻信號和低頻信號，并且將低頻信息進行重構，將重構的信息進行相關性分析，這種方法既縮減了信息維數，又去除了信息噪聲，通過搖擺曲線基本升降規律識別同調機群，但是此方法計算量大。

同調機群的識別其本質是一個聚類問題，即將同調的機組聚集在一起，不同調的機組分開。同調機組的聚類方法主要包括相關系數法［11］、層次分析法［12］、模糊聚類法［13］等。對于大系統而言，這些方法一般比較復雜，計算量大，不適合于大數據的處理。文獻［14］提出把Kohonen自組織神經網絡運用到同調識別，適合大數據的處理，但是需要預先指定競爭層網絡單元數目及其機構形狀。

考慮到同調機群識別中存在的上述問題，首先使用小波變換的多尺度空間能量分布特征的提取方法提取機組功角搖擺曲線特征向量，然后將小波能量特征和時頻域特征組合，作為增長型自組織神經網絡的輸入向量，在保證信號特征全面的情況下降低了特征的維度，通過控制閾值λ，最終在輸出層得到不同精度的分群結果。最后通過10機IEEE-39節點系統驗證了此方法的計算量小，計算速度快，聚類結果具有更高的穩定性和準確性。

1 同調機組分群理論

發電機的同調性是指當系統運行方式改變或受擾后，系統中發電機功角變化呈現出相似的規律［15］。關于同調機群的定義多種多樣，最常用的定義如下，在計算時間t∈［0，T］內滿足：

式中 Δδi=δi-δi0；Δδj=δj-δj0；δi、δj為發電機i、j的實時功角；δi0、δj0為發電機i、j的功角初值；Δδi、Δδj為發電機功角的實時變化量；ε是發電機之間同調程度的度量值。

但考慮到當兩臺機組i，j擺幅都很小，并且一臺機組搖擺曲線上升，另一臺機組搖擺曲線下降的情況下也很有可能滿足式（1），而此時兩臺機組明顯不同調。因此利用相關性來定義機組同調：

k可以取任意常數使得Sij最小，令：

可求出：

綜合式（1）和式（4），定義機組同調識別判據為：

式中α為最大最小原則比重系數；β為均方根準則比重系數（本文取α=0.6、β=0.4）。當ε=0時，即發電機功角搖擺曲線走向完全一致，稱發電機完全同調；當ε＞0，即發電機功角搖擺曲線最大差為ε，稱發電機ε-同調。在實際應用中，沒有完全同調的發電機，所以一般使用ε-同調。

將滿足式（5）的發電機視為同調機組，不滿足式（5）的發電機視為不同調機組，這樣通過劃分外在功角搖擺曲線實質劃分發電機內在特性的過程就是機組同調識別。

2 小波能量特征提取

以短時傅里葉變換為過渡發展起來的小波變換，同時具有良好的時域趨勢描述、頻域局部特征刻畫功能，克服了傅里葉變換在時域上不能定位的缺點，并且小波的選取非常靈活，適合分析瞬時非平穩信號，被廣泛應用于特征提取［16］。

對功角搖擺曲線在多尺度空間進行小波分解，信號被分解為多個頻段，低頻段之前的系數為逼近系數，高頻段之前的系數為細節系數，合稱為小波系數，它們蘊含著大量反映搖擺曲線特征的信息。通過小波系數計算各個頻段的小波能量，并且按頻次由大到小的順序排列，構成小波能量特征向量，這就是小波變換多尺度空間能量分布特征的提取方法［17］。

假設f∈L2（R）是發電機的功角搖擺曲線，測量信號fj是f在尺度空間Vj的近似，則fj的多尺度分解可表示為：式中fj-k和wj-k分別為fj在空間Vj-k和Wj-k的逼近和細節。

為了計算快速方便，采用二進小波變換中的Mallat算法實現［18］。利用Mallat算法對功角搖擺曲線逐層分解，每一層的逼近系數通過一組高通濾波器和低通濾波器得到下一層的逼近系數和細節系數［19］。功角搖擺曲線f（k），k=1，2，...，M，其二進小波分解Mallat算法如下：

式中M是功角搖擺曲線f（k）的采樣點數；j是分解的層數；hn-2k，gn-2k分別是低通濾波系數和高通濾波系數；分別是功角搖擺曲線f（k）在分辨率2j-1下的逼近系數和細節系數；

對功角搖擺曲線f（k）進行兩層小波分解，被分解為三個頻段，其中逼近系數為Ca2，細節系數為Cd1、Cd2。

提取小波變換多尺度空間能量特征的步驟如下：

首先給出小波能量定義，功角搖擺曲線f（k）在子空間Wj中小波能量定義為：

（1）確定信號各頻段小波系數的總能量，如下：

（2）構造小波能量特征向量。依次計算各個頻段的小波能量值，并且按照頻段順序排列組合為特征向量：

利用上述流程可以對機組功角搖擺曲線信號進行特征提取，提取出可以代表搖擺曲線的特征向量數據。即完成從搖擺曲線信號到特征向量數據的轉換。

3 自組織神經網絡模型學習算法

增長型自組織神經網絡不需要事先設定競爭層神經元的個數，而是隨著閾值λ的改變，自動生成不同數量的競爭層神經元。該方法不受樣本輸入順序的影響，聚類結果準確穩定，被廣泛應用于聚類分析［20］。

3.1 增長型自組織神經網絡結構

自組織神經網絡和一般神經網絡相比，沒有隱含層，只有由權值連接的輸入層和競爭層。如圖1所示。輸入層輸入樣本的特征向量，其中輸入層神經元的個數等于樣本特征向量的維數。競爭層輸出樣本的分類結果，競爭層神經元的個數等于最終的分類組數。競爭層神經元個數是逐漸變化的，隨著輸入樣本的增加，樣本屬于不同類別的數量就會增加，競爭層神經元的個數也就跟著增加。

圖1 自組織特征映射神經網絡結構圖Fig.1 Self-organizing neural network structure diagram

式中Xi為輸入向量；Wij為第j類組別模式的聚類中心；Dj為歐氏距離。

3.2 增長型自組織神經網絡學習算法

增長型自組織神經網絡屬于無導師學習型網絡，不需要先驗知識的引導，自動形成組群分類。該算法主要包括以下步驟：

（1）設置閾值λ。λ可以控制聚類結果的精細程度，聚類結果隨著λ的增大而變粗。在聚類前，通過試算λ值以應對不同聚類情況；

（2）初始化權值。樣本輸入特征向量為：Xi=［xi1，xi2，...，xiN］T；N是樣本輸入特征向量維數；i為樣本數量。初始令競爭層神經元個數為j=1，將任意樣本輸入特征向量作為輸入層與競爭層的連接權值Wij；

（3）競爭分類。輸入一個新的樣本，計算其與競爭層神經元的歐氏距離Dj，歐式距離最小的競爭神經元p獲勝：Dp=min｛Dj｝；

（4）更新權值。如果Dp＜λ，則將該樣本納入競爭神經元k代表的組別模式，同時更新連接權值：Wij（n+1）=Wij（n）+η（n）（Xi-Wij（n）），η（n）是納入第j個動態類型納入樣本數的倒數。然后轉入第（3）步；

（5）更新競爭層。如果Dp＞λ，則該樣本不納入任何一個競爭神經元代表的組別模式，并且更新競爭層神經元數量j=j+1，該樣本代表新的組別模式，

輸入層與競爭層中的連接權值起著中心指引的作用，相當于整個自組織神經網絡的分析系統，能夠記憶每個競爭神經元代表的組別模式，隨著樣本劃分到不同的競爭神經元，新增樣本的競爭神經元的連接權值也要更新。當一個樣本的特征向量與一個競爭神經元的連接權值相似到一定程度時，那么該競爭神經元就將其納入本組，否則，該樣本不屬于任何現有競爭神經元，需要新增一個競爭神經元，并用其連接權值記憶新的樣本模式［21］。

增長型自組織神經網絡樣本輸入向量為N個功角搖擺曲線的特征，競爭層神經元不斷更新的連接權值稱為該模式組別的聚類中心，根據輸入特征相似程度將樣本劃分到不同的組別模式中，使得功角搖擺曲線變化趨勢相似的發電機聚集在一起，不同的分開，輸入向量和組群中心的相似程度用距離來衡量，本文采用歐氏距離［22］：新組別模式與輸入層的連接權值Wij（n+1）為該樣本輸入特征向量；

（6）依次循環。當全部樣本被納入競爭神經元結束。競爭神經元個數j就是聚類組數，每個競爭神經元納入的樣本為具體分類結果。

上述增長型自組織神經網絡學習的過程就是神經網絡的構建模型的過程，當有新的實時樣本時，只需將新樣本輸入模型，在競爭層即可得到最終的分類結果，每個競爭神經元代表不同的組別模式。

3.3 最優閾值λ的確定

當給定一個λ值時，系統機組被劃分為K類，即將系統中時序功角數據集 D=｛d1，d2，…，di，…，dN｝劃分為K個簇｛C1，…，Cj，…，CK｝，其中di∈Rm；N為系統發電機數量；m為時序功角向量維度。每個簇都有各自的聚類中心cj，計算所有簇內各個數據點到聚類中心cj的歐式距離的平方和J（C），其函數值的大小反映了聚類結果的優劣。

顯然，每個K值都對應一個函數值J（C）。當K值較小時，每個簇的歐氏距離很大，隨著K值的增大，函數J（C）減小的非常快。此時樣本快速分堆，具有相似特性的樣本聚集在一起，聚類效果迅速優化；當K值較大時，每個簇的歐式距離已經很小，繼續增大K值，函數J（C）的變化將不再明顯，此時聚類結果已達到最優。J-K關系曲線如圖2所示，圖中的拐點可確定最優的分類K值，進而根據該分類K值就可以得到最優的閾值λ。

圖2 J-K關系曲線Fig.2 J-K relationship curve

4 算例分析

4.1 同調機群識別流程

選取發電機功角曲線的局部超調量d1ij和全局能量d2ij作為功角搖擺曲線時域特征［6］；選取發電機功角曲線的主頻成分ωmax作為功角搖擺曲線頻域特征；根據上述小波能量特征提取方法，構建小波能量特征向量 F=［Ei0，Ei1，Ei2］。綜合時頻域特征、小波能量特征，構成神經網絡發電機樣本輸入向量為：G*i=［d1ij，d2ij，ωmax，Ei0，Ei1，Ei2］，并且將其歸一化：

以PSD-BPA為電力系統仿真平臺，模擬線路出現故障模式，對電力系統進行故障模擬仿真。根據上文所訴內容編寫計算機程序。程序流程如圖3所示。

圖3 程序流程圖Fig.3 Program flow chart

4.2 IEEE-39節點仿真分析算例

為驗證本文方法的有效性，以IEEE-39節點系統為例進行聚類分析，該系統包括39個節點，10臺發電機，其中31號發電機節點為平衡節點，30、32、33、34、35、36、37、38、39號發電機節點為 PV節點，負荷為恒定阻抗。IEEE-39節點系統如圖4所示。

圖4 IEEE 39節點系統接線圖Fig.4 Wiring diagram of IEEE 39-bus system

分別以發電機G30、G32為參考機，設BUS-3處發生三相斷路故障，故障持續時間0.12 s。切除故障前后網絡的拓撲結構保持不變。在BPA中得到每個發電機的功角變化數據，并經過Matlab處理后分別如圖5、圖6所示。

圖5 IEEE 39發電機功角搖擺曲線Fig.5 IEEE 39 generators power angle of the rocking curve

圖6 IEEE 39發電機功角搖擺曲線Fig.6 IEEE 39 generators power angle of the rocking curve

樣本參數為S=｛G30，G31，G32，...，G39｝。首先只考慮時頻域特征作為特征向量，構成10×3特征參數矩陣，將其輸入自組織神經網絡進行訓練，得到的識別結果如表1所示；然后同時考慮小波能量特征和時頻域特征作為特征向量，構成10×6特征參數矩陣，將其輸入增長型自組織神經網絡進行訓練，得到的識別結果如表2所示。

表1 只考慮時頻域特征的同調機群劃分結果Tab.1 Coherent cluster division results when considering only the frequency domain characteristics of the coherent cluster division results

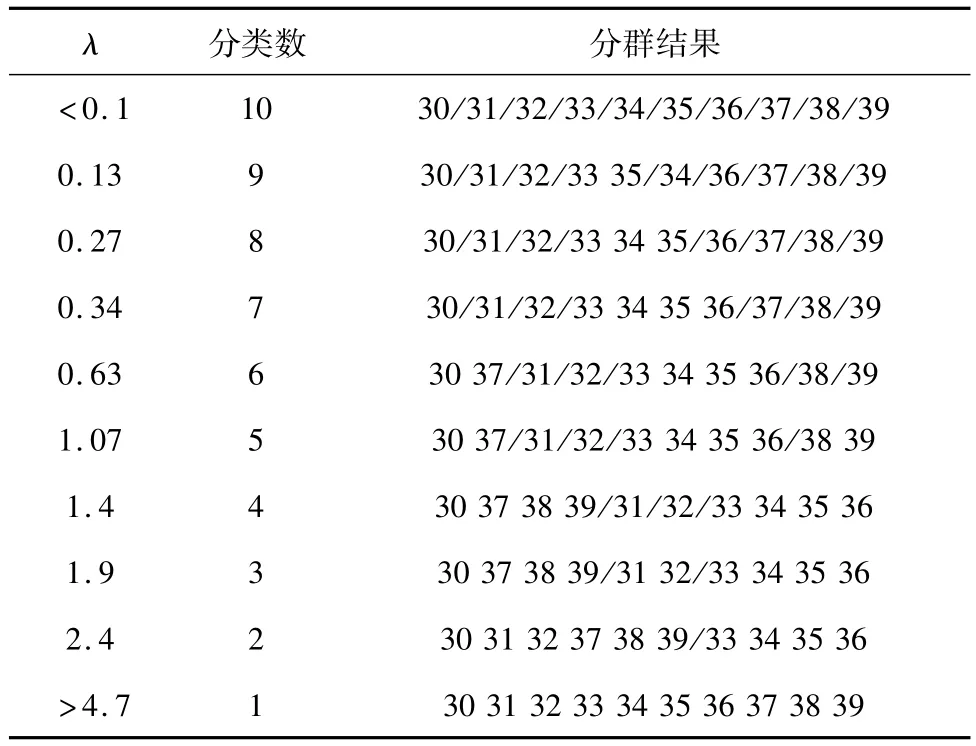
表2 同時考慮小波能量特征和時頻域特征的同調機群劃分結果Tab.2 Coherent fleet division results when taking into account the characteristics of wavelet energy and time frequency domain features coherent fleet division results

從表1可以看出，當分類數為6時，只考慮時頻域特征的分類結果為：｛30｝｛31｝｛32｝｛37｝｛33，34，35，36｝｛38，39｝。從表2知，同時考慮小波特征和時頻域特征且分類數為6時，分類結果為：｛30，37｝｛31｝｛32｝｛33，34，35，36｝｛38｝｛39｝。按式（5）計算的同調判據值進行分析，1.5 s之內G38、G39同調判據值為0.075，G30與G37的同調判據值為0.053 5，G30與G37的同調性要強于G38與G39，從圖6也能直觀看出來，G30、G37的同調性明顯比G38、G39更強。因此，同時考慮小波特征和時頻域特征的分群結果更為合理。

當分類數為4時，只考慮時頻域特征，分類結果為｛30，37｝｛31，32｝｛33，34，35，36｝｛38，39｝。同時考慮小波特征和時頻域特征的分類結果為｛30，37，38，39｝｛31｝｛32｝｛33，34，35，36｝。在1.5 s之內G31、G32按式（5）計算同調判據值為0.270 6。而G30、G37、G38、G39相互之間按式（5）計算的同調判據最大值為0.148 0。可見，將｛30，37，38，39｝聚為一類是合理的。因此，同時考慮小波特征和時頻域特征的分群結果明顯要優于只考慮時頻域特征的分群結果。

綜上所述，同時考慮小波能量特征和時頻域特征比只考慮時頻域特征作為增長型自組織神經網絡輸入向量具有更高的準確性，驗證了所提出的方法更為有效。

5 結束語

提出了一種新的基于小波變換多尺度空間能量分布特征和增長型自組織神經網絡的同調機組分群方法。改進了同調機群識別的判據，利用小波變換多尺度空間能量分布特征的提取方法提取機組功角搖擺曲線信號的特征，并結合時頻域特征構成輸入特征向量，減少了特征維數。利用融合自適應共振理論和Kohonen網絡基本思想改進了自組織神經網絡，克服了自組織神經網絡需要預先給定競爭層網絡單元數目及結構形狀的問題。仿真算例可以看出，同時考慮小波能量特征和時頻域特征的聚類方法比只考慮時頻域特征具有更高的聚類準確性。