圓柱殼體裝藥偏心多點起爆下破片速度的分布＊

沈慧銘，李偉兵，王曉鳴，李文彬，董曉亮

圓柱殼體裝藥偏心多點起爆下破片速度的分布＊

沈慧銘，李偉兵，王曉鳴，李文彬，董曉亮

（南京理工大學智能彈藥技術國防重點實驗室，江蘇 南京210094）

針對偏心起爆戰斗部破片速度增益的問題，提出爆轟波碰撞形成馬赫超壓是引起破片速度增加的原因。利用AUTODYN軟件，模擬偏心起爆戰斗部從殼體徑向膨脹、表面產生裂紋到最后形成破片的整個過程，并將模擬得到的破片速度與實驗數據對比，兩者吻合較好；簡化Whitham方法并結合Gurney速度公式得到偏心起爆戰斗部定向破片速度和定向區域的計算方法，同時在保證破片初速的前提下，研究偏心多點起爆下起爆點數的選擇標準。研究結果表明：偏心多點起爆下定向破片初速增益約34%，定向區域范圍約30°，起爆點數的選擇與殼體長度和裝藥口徑相關。

定向戰斗部；馬赫反射；偏心多點起爆；破片初速

偏心起爆戰斗部是一種定向戰斗部，它利用爆炸邏輯網絡實現偏心起爆，可以使破片在定向方向上的速度大大增加，從而達到高效毀傷的目的。定向戰斗部是近年來殺傷爆破戰斗部的研究重點，如王樹山等［1］實驗研究預制桿狀破片戰斗部、側面四點偏心起爆下破片徑向飛散規律，發現偏心起爆能顯著增加定向方向的破片初速及破片數；黃靜等［2］比較了三種不同夾角的偏心線起爆方式下，破片速度增益情況，研究結果表明夾角45°雙線起爆對破片初速提高最大，增益超過30%；張博等［3］將偏心多點起爆、偏心單點起爆以及中心點起爆三種起爆方式下隨機破片戰斗部的初速、破片利用率和目標定向區域進行對比，發現偏心多點起爆方式較優。根據前人對于定向戰斗部的研究，可以看出偏心多點起爆戰斗部在破片初速等方面有一定的優勢。

本文中針對偏心多點起爆戰斗部，探索提高偏心戰斗部破片速度的主要因素，利用AUTODYN軟件［4］，模擬偏心起爆戰斗部破片形成的過程，分析破片速度分布規律，簡化文獻［5］中Whitham計算馬赫流場的方法和Gurney速度公式［6］，提出偏心多點戰斗部定向破片的初速計算方法以及定向區域的大小。由于線起爆方案結構復雜且不易實現，所以工程實際中還是主要采用多點偏心起爆方案代替線起爆方案，通過起爆點數的選擇來充分發揮炸藥中馬赫超壓的作用提高破片初速，也是研究的重點。

1 模型驗證

為驗證數值模擬可靠性，采用AUTODYN－3D軟件模擬單點、中心起爆方式下圓柱形殼體在炸藥爆轟作用下破片初速軸向分布情況并與G.Y.Huang等［7］的實驗結果對比。

1.1 數值模擬

對于自然破片戰斗部，理論上大多采用Mott分布［6］來描述破片的質量分布，而數值模擬中運用Stochastic模型［4］模擬殼體材料隨機破壞，該模型是一種基于概率統計方法來表征物質的固有缺陷分布來產生破壞和裂紋的模型，在材料離散化模型內隨機添加一些弱化點，設定弱化點處網格應變不能承受負壓力或剪應力，這樣可定性描述離散幾何體模擬真實材料的破壞模式，根據不同分布的Stochastic模型得到不同數量和大小的破片。有限元模型如圖1所示，整個計算模型簡化為炸藥、殼體兩部分，模型中殼體長度L＝77.3mm，殼體的外徑Re＝29.68mm，殼體的內徑Ri＝23.6mm（與G.Y.Huang［7］的實驗尺寸相同）。模型關于兩個對稱面對稱，故只需建立1／4模型，均采用Lagrange算法，因為殼體材料的破碎、破片的形成過程是一個大變形的彈塑性流體動力學過程，采用Lagrange算法雖然網格會發生較大的扭曲變形，但該方法對介質運動的整體和局部的變化都有更清晰的描述，能真實的呈現殼體膨脹、裂紋產生、破片形成的整個過程，也能更清楚的顯示節點的速度、整體的動能等物理量。

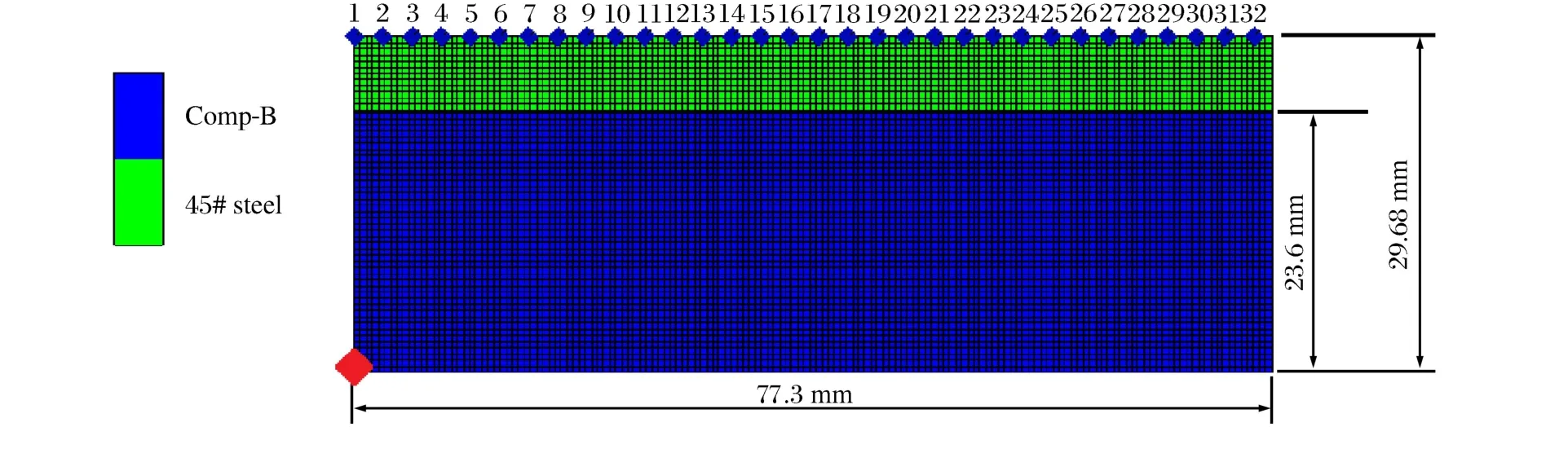
圖1 有限元模型Fig.1Finite element model

炸藥為Comp－B，密度為1.717g／cm3，采用高能炸藥 MAT＿HIGH＿EXPLOSIVE＿BURN 材料模型，Johns－Wilkins－Lee狀態方程［4］描述高能炸藥及其爆轟產物的膨脹過程，JWL狀態方程形式為：

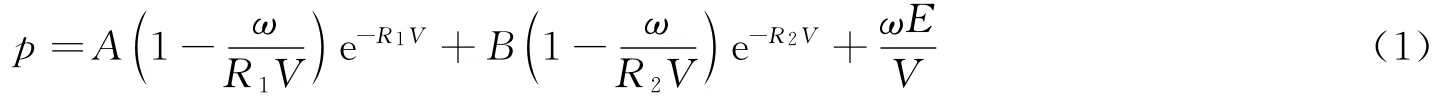
式中：A、B、R1、R2和ω為實驗室測定的常數，E為比內能，具體參數見文獻［8］；殼體材料為45鋼，采用Johnson－Cook材料模型［4］描述殼體在炸藥載荷下的高應變率效應和熱軟化效應，Grüneisen狀態方程定義了壓力和體積之間的關系，用于描述45鋼在高壓下的行為。Johnson－Cook本構方程的形式為：

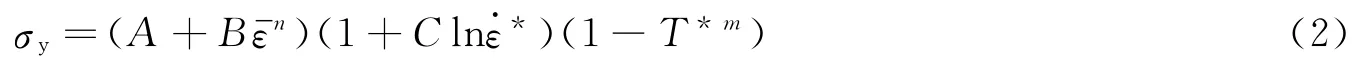
式中：σy為 Von Mises等效應力。材料參數 A＝0.335GPa，B＝0.30GPa，C＝0.014，n＝0.26，m＝1.03；ε為等效塑性應變為量綱一塑性應變率，其中ε0為參考應變率，一般取1s－1；T＊＝為量綱一溫度，其中Tr和Tm分別為室溫和材料的熔化溫度。

在爆炸內部載荷作用下殼體膨脹和破裂的過程如圖2所示。接近起爆點處的殼體首先發生徑向膨脹且逐漸傳播至整個殼體，至20μs時刻殼體隨機產生裂紋，隨著時間增加殼體最終破碎且形成破片。在軸線方向上，由于稀疏波的傳入，殼體中心處破片初速比兩個端部要高。實驗和數值模擬得到的破片軸向速度列于表1，破片速度分布見圖3所示。

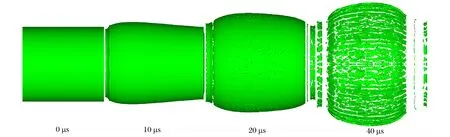
圖2 中心單點端面起爆破片形成示意圖Fig.2Process of the fragment formation under center detonation with single point

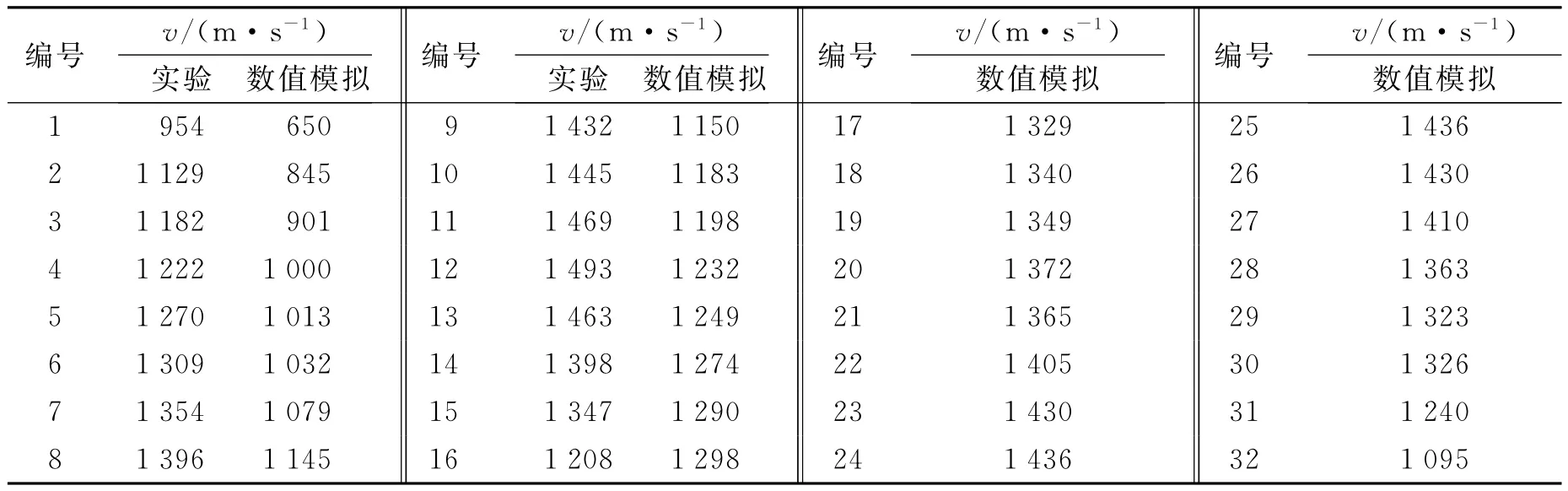
表1 實驗數據與理論模型結果對比Table 1Comparison between experimental and theoretical data

從圖3中可以看出殼體兩個端部的破片速度要明顯較低，中心處破片初速較高，且起爆端面破片初速要低于非起爆端面的初速；數值模擬得到破片速度最高值為1 436m／s，實驗中最大值為1 493m／s，誤差約為3.8%。數值模擬和實驗中破片速度分布吻合較好，主要偏差出現在兩個端部：在x＝0和x＝77.3mm位置，數值模擬得到破片速度分別為650和1 050m／s；實驗值為954和1 208m／s。差距較大的原因可能是因為在數值模擬中炸藥的JWL狀態方程是假定爆轟產物以常速率傳播，而實際中炸藥爆轟波前沿是一個加速的過程，導致模擬中稀疏波過早的傳入，端部爆轟波陣面的壓力降低，從而計算出的破片速度也隨之減小。總體來看，破片速度分布規律的數值模擬結果和實驗結果吻合較好，可以認為數值模擬方法能準確預測破片的速度分布。

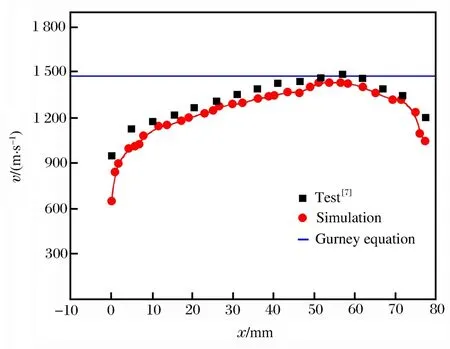
圖3 不同位置處破片初速的變化Fig.3Variation of initial velocity of fragments at different positions

2 偏心多點起爆

2.1 理論模型

偏心多點起爆，當起爆點數足夠多時，可以看作偏心線起爆。兩線偏心起爆時，其截面結構和狀態處處相等，可轉化為任一截面兩點對稱起爆，從而簡化為平面爆轟波的馬赫反射問題。如圖4所示，起爆點連線為兩條直線，位于炸藥的同一側且關于水平軸對稱，為了計算的方便，起爆點設置在和圓心的連線與x軸夾角為45°的位置。

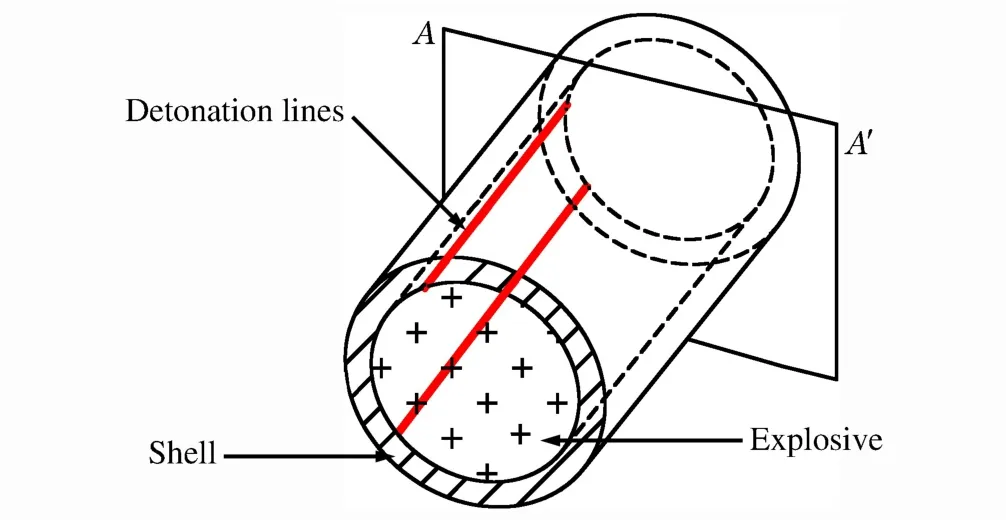
圖4 偏心起爆戰斗部分析模型Fig.4Analytic model of eccentric warhead

2.2 定向區域及定向破片初速的計算

對于馬赫反射區流場的計算［5］本文中不在贅述。定向戰斗部爆轟波碰撞示意如圖5所示，為了得到定向區域的大小，需要進行兩步工作：（1）馬赫反射初始坐標計算；（2）三波點的運動軌跡。

根據Whitham方法，采用激波極曲線法，可以得到馬赫反射的臨界角ψc，根據幾何關系可得馬赫反射初始位置的坐標：

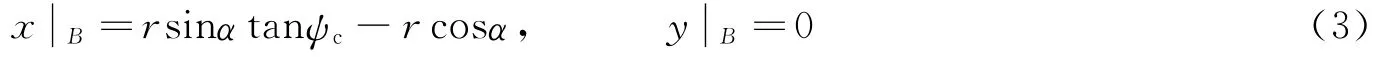
當入射波的強度和入射角隨時間變化時，馬赫桿波的增長速度是變化的，相應的三波點的軌跡是一條曲線。由于馬赫桿波是變強度的，所以這種情況的理論分析和計算相當復雜，不利于工程實際中應用。在不影響分析和結論的前提下，為了便于處理，將三波點的運動軌跡近似認為是直線。設三波點運動軌跡與固壁的夾角為φ，可以得到較簡單的三波點軌跡：

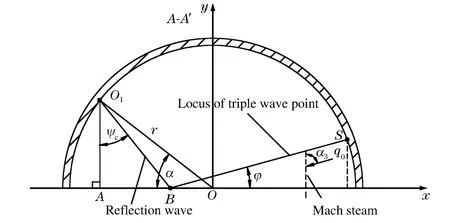
圖5 爆轟波碰撞示意圖Fig.5Diagram of detonation wave collision

式中：α3為馬赫桿與介質流動速度的方向之間的夾角，其中q0、p0、ρ0為未反應區介質的流動速度、壓力和密度；p3、ρ3為馬赫反射區介質的壓力和密度，將α3的表達式代入式（4）即可求出定向區域大小。由于圖5只給出了二分之一模型，故圓柱殼體裝藥偏心多點定向戰斗部的定向區域為2φ。

已知裝藥和殼體參數情況下，由Gurney速度公式易得定向破片的初速：

式中：β為馬赫區裝填比（炸藥質量與殼體質量的比值），D為馬赫波到達殼體壁面時速度，計算中可直接簡化為馬赫波波速。

2.3 數值模擬及結果分析

建立偏心多點定向戰斗部模型，在裝藥一側設置兩條起爆線，每條起爆線上設置15個起爆點，如圖6所示。炸藥起爆，殼體在爆轟產物的高壓作用下膨脹破碎，參見圖7，γ表示圓心角。圖中可以看出定向區域破片突出明顯，表明該區域破片速度較高。在戰斗部橫截面360°范圍內破片初速統計，得到偏心多點起爆下破片初速分布，見圖8。

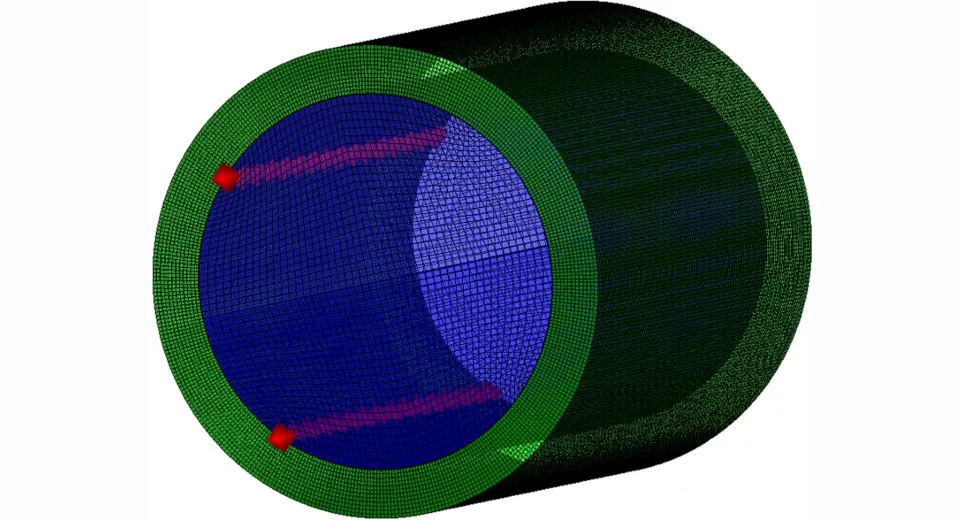
圖6 偏心多點定向戰斗部有限元模型Fig.6Simulation model of directed fragmentation warhead

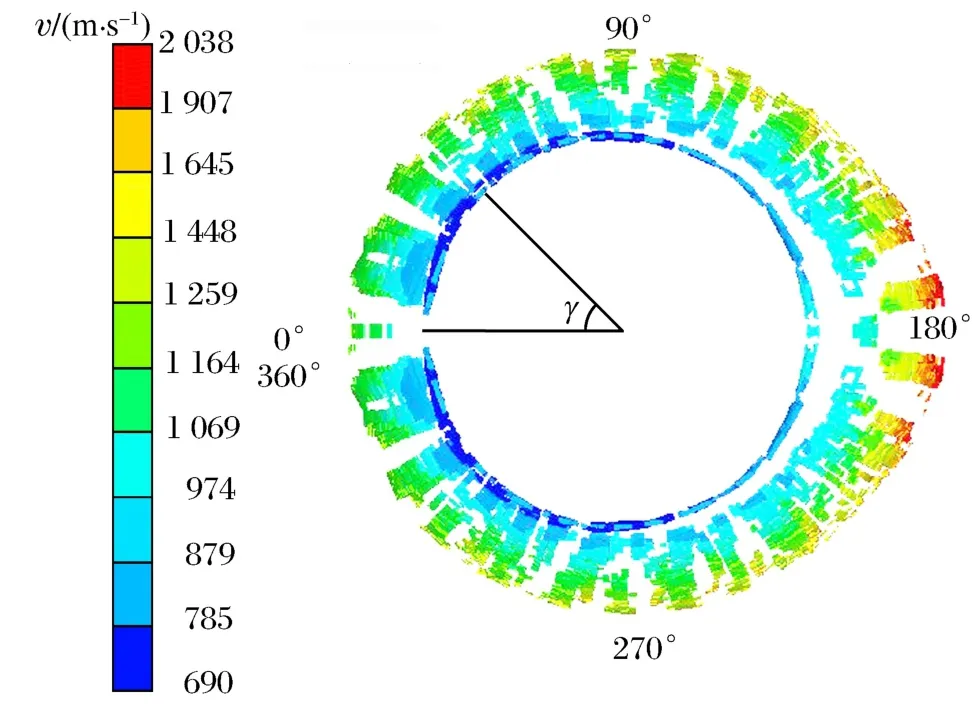
圖7 35μs時刻破片飛散形態Fig.7Fragment dispersion at 35μs

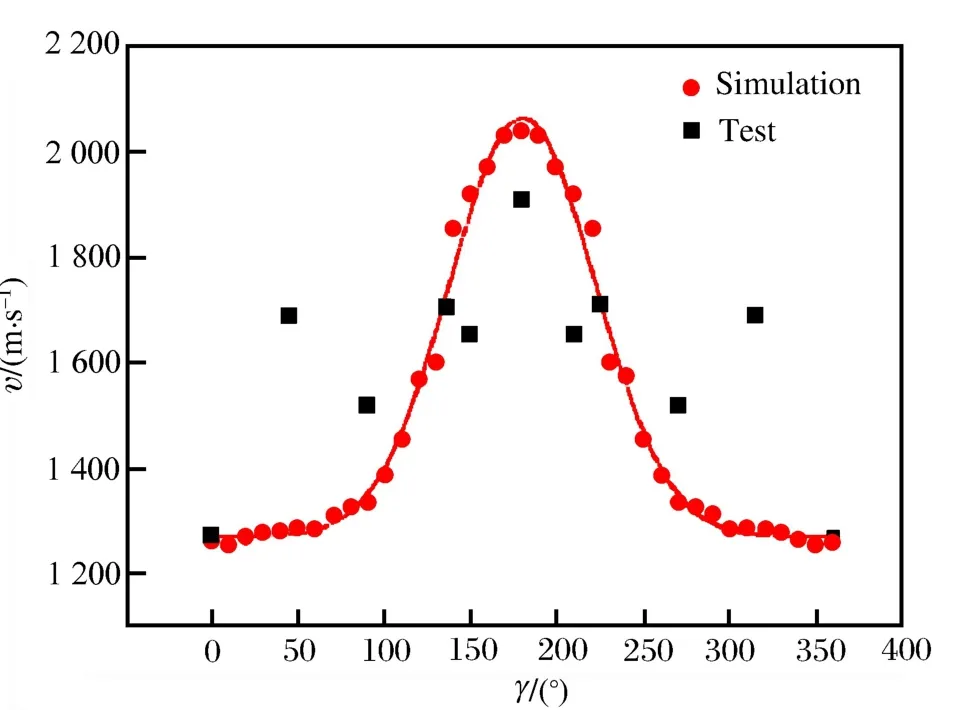
圖8 破片速度分布Fig.8The fragment initial velocity distribution

定向破片初速在1 900～2 050m／s的范圍內，其中最大速度為2 038m／s，與理論模型計算得到的結果2 073.4m／s相近。相對中心點起爆，定向破片初速提高了約34%，由于動能是速度的平方項，所以破片的動能毀傷提高更大。

為了清晰準確的比較馬赫超壓作用區域，建立圖9所示的二維有限元模型。因為采用Lagrange算法，炸藥和鋼之間必須留有少量空隙，模型尺寸和材料參數等與前文相同。

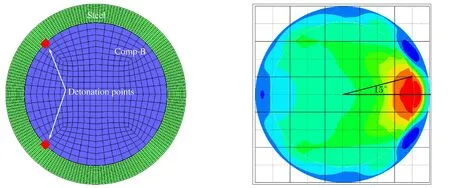
圖9二維有限元圖和壓力云圖Fig.9Two－dimensional numerical model and stress nephogram

圖9 為裝藥爆轟后7μs時刻爆轟壓力作用于殼體的壓力云圖，可以清楚的看出定向區域的壓力明顯高于其他部分，測量該區域的夾角為15°，與理論模型的計算值15.2°非常接近。偏心多點起爆下定向戰斗部的定向區域和定向區域的破片初速的理論計算與數值模擬吻合較好，相互佐證。

2.4 起爆點數選擇

前面的模擬中選擇足夠多（15個）的起爆點來代替線起爆，但是隨著點數增加起爆的同步性越難保證，而點數太少則爆轟不完全，破片初速降低，所以選擇合理的起爆點數值得進一步研究，即保證破片初速的前提下選擇最少的起爆點。

為找出點代線的規律，在單軸起爆線上均布1～5個起爆點，計算得到不同起爆點數下，破片初速的分布情況與15個起爆點線起爆進行對比，如圖10所示。

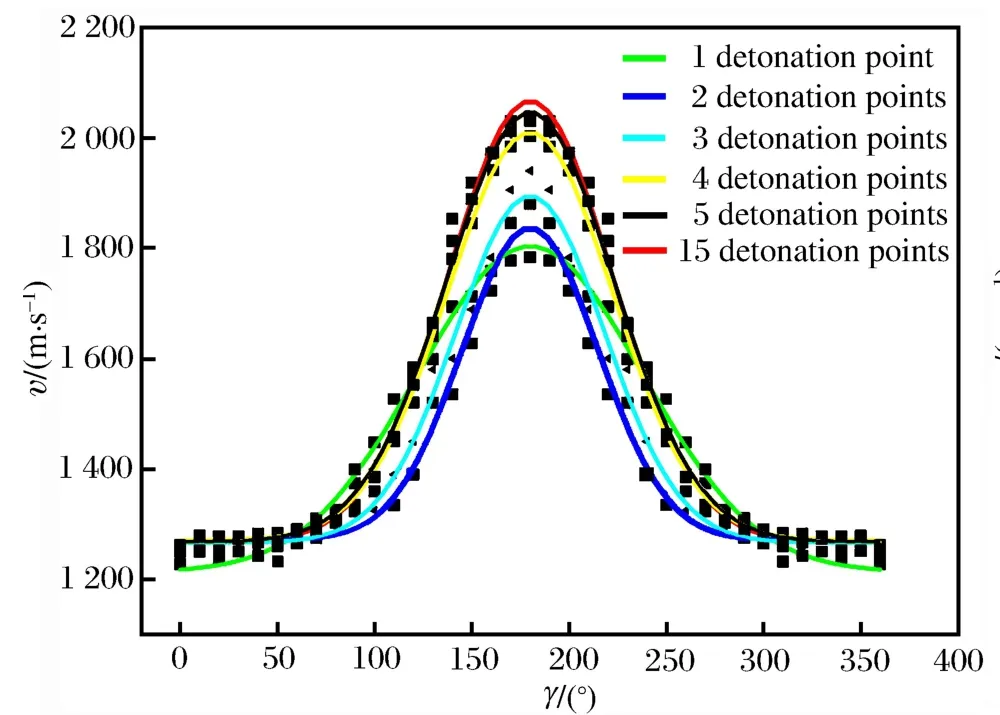
圖10 不同起爆點數下破片速度比較Fig.10Comparison of fragment initial velocities under different number of detonation points

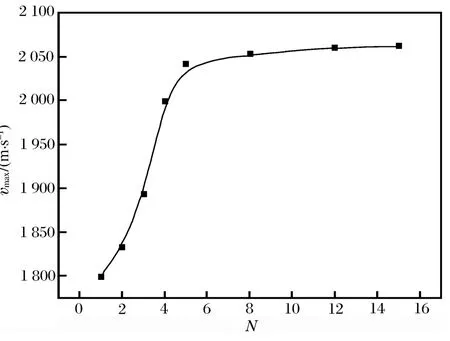
圖11 破片最大速度隨爆點點數的變化Fig.11Variation of fragment maximum velocity with detonation point number

分析圖10發現，隨著起爆點的增加，定向破片初速也逐漸增大，因為當起爆點較少時，馬赫反射不充分，只有靠近起爆點的部分區域產生馬赫超壓，不能完全發揮出所有炸藥的潛能。圖11所示為定向破片最大速度隨起爆點數變化曲線，可以發現當單軸的點數從1增加到5，破片最大速度提高了242.2m／s，提高約13.5%；當點數繼續增加，直至線起爆，破片最大初速僅提高了20m／s，速度提高不到1%。所以對于本文的模型結構尺寸，5點起爆可以代替線起爆。

對于任意尺寸的定向戰斗部，殼體長度L、裝藥口徑d、單軸點代線的點數為N。假設存在一個參數η與殼體長度L、裝藥口徑d相關：

式中：η定義為相鄰起爆點間距與裝藥口徑的比值，是量綱一常數，是多點起爆代替線起爆的標準。由本文中的計算模型可計算出η≈0.819。則對任意尺寸定向戰斗部，偏心多點起爆點代線的點數為：

3 實驗驗證

采用數值模擬相同的裝藥結構，見圖12，圓柱殼體兩線偏心起爆，每條起爆線上均布5個起爆點來代替線起爆。

測速方法將測時儀法和高速攝像法兩者相結合。在戰斗部周圍不同方向（0°、50°、90°、140°、160°和180°）上布置錫箔靶紙，靶紙與多通道計時儀連接，破片擊穿靶紙時計時儀收到一個“通信號”開始計時，破片擊穿下一張靶紙時，計時儀收到下一個“通信號”計時結束，則計時儀記錄到破片穿過兩張靶紙所用的時間，從而計算出破片穿過兩靶的平均速度，通過速度衰減公式易得出破片初速；同時在距爆炸中心10m處架設高速攝影儀，并用高速攝像法進行測速，實驗測得的破片速度與數值模擬結果在圖8中表示。

對比實驗和數值模擬結果可以發現，實驗測得的破片速度要比數值模擬得到的速度普遍偏小，主要因為實驗中需要在殼體上開小孔來插入雷管，爆炸產物在小孔處泄壓，所以破片速度偏小；在50°方向上破片速度遠高于數值模擬的速度，分析原因，該方向處于雷管飛散的方向，可能是雷管引爆后雷管殼碎片擊穿錫箔靶觸發計時儀計時，從而導致測得的速度遠大于數值模擬結果。總體而言，實驗和數值模擬結果吻合較好，誤差在10%以內。

圖12 偏心起爆戰斗部實驗Fig.12Test of eccentric initiation warhead

4 結 論

本文中分別通過數值模擬和實驗的方法研究中心起爆方式下破片軸向初速分布以及偏心多點起爆方式下定向戰斗部破片初速分布規律和定向區域的范圍；理論上簡化了Whitham方法并結合Gurney速度公式分析偏心多點起爆下定向破片初速的計算方法和定向區域的計算方法；最后在保證破片初速的前提下，研究點代線的規律，得出如下結論：

（1）數值模擬的中心起爆方式下破片軸向初速分布與實驗結果吻合較好，說明基于Mott破片分布理論的Stochastic隨機破碎模型，以及采用的材料參數，能較全面較準確的模擬戰斗部隨機破片的飛散特性，可以為破片戰斗部數值模擬方法提供一定的參考；

（2）定向戰斗部相較周向均勻戰斗部定向破片初速增益為34%，定向區域約30°；利用Whitham方法計算定向區域，結合Gurney速度公式得到定向破片初速的計算方法，其理論計算結果與數值模擬結果很接近，可為定向戰斗部的研究提供理論上的支持；

（3）得到偏心戰斗部點代線的點數選擇的公式；對于任意尺寸戰斗部都具有一定的工程應用價值。

［1］ 王樹山，馬曉飛，隋樹元，等.偏心多點起爆戰斗部破片飛散實驗研究［J］.北京理工大學學報，2001，21（2）：177－179.Wang Shushan，Ma Xiaofei，Sui Shuyuan，et al.Experimental research on fragments dispersion of the warhead under asymmetrical multi－spots initiation［J］.Journal of Beijing Institute of Technology，2001，21（2）：177－179.

［2］ 黃靜，孔凡勛，袁晉等.多點偏心起爆對破片速度增益的影響［J］.現代防御技術，2011，39（6）：37－42.Huang Jing，Kong Fanxun，Yuan Jin，et al.Influence of multi－spots off－axis initiation on fragment velocity gain［J］.Modern Defence Technology，2011，39（6）：37－42.

［3］ 張博，李偉兵，李文彬，等.偏心起爆戰斗部隨機破片數值仿真［J］.高壓物理學報，2012，26（4）：442－448.Zhang Bo，Li Weibing，Li Wenbin，et al.Numerical simulation of the dispersion of random fragments under asymmetrical initiation［J］.Chinese Journal of High Pressure Physics，2012，26（4）：442－448.

［4］ Century Dynamics Inc.AUTODYN theory manual revision 4.2［M］.San Ramon：Century Dynamics Inc，2001.

［5］ 糜仲春.馬赫反射研究進展［J］.力學進展，1982，12（1）：41－50.Mi Zhongchun.Recent advances in mach reflection［J］.Advances in mechanics，1982，12（1）：41－50.

［6］ 黃正祥，祖旭東.終點效應［M］.北京：科學出版社，2014：83－102.

［7］ Huang G Y，Li W，Feng S S.Axial distribution of fragment velocities from cylindrical casing under explosive loading［J］.International Journal of Impact Engineering，2015，76（2）：20－27.

［8］ 耿荻，馬天寶，寧建國.定向戰斗部爆炸驅動規律研究［J］.爆炸與沖擊，2013，27（5）：685－690.Geng Di，Ma Tianbao，Ning Jianguo.Study on laws of explosive driven behaviors of aimed warhead［J］.Chinese Journal of High Pressure Physics，2013，27（5）：685－690.

［9］ 王繼海.二維非定常流和激波［M］.北京：科學出版社，1994：82－100.

Velocity distribution of fragments resulted by explosion of a cylindrical shell charge on multi－spots eccentric initiation

Shen Huiming，Li Weibing，Wang Xiaoming，Li Wenbin，Dong Xiaoliang
（Ministerial Key Laboratory of ZNDY，Nanjing University of Science and Technology，Nanjing210094，Jiangsu，China）

To address the issue of the increase of the fragment velocity of an eccentric initiation warhead，we put forward the view that this increase was caused by the Mach overpressure formed by the detonation wave collision.We used the AUTODYN software to simulate the whole explosion process of the eccentric initiation warhead，from the radial expansion of the shell to the formation of the surface cracks，and eventually the formation of the fragments.We then compared the simulation result of the fragment velocity with the test data and found that they were in good agreement.Further we combined the simplified Whitham method with the Gurney equation to obtain the calculation method of the directional fragment velocity and directional area of the eccentric initiation warhead.We studied the selection criteria for the number of the initiation spot on the premise of maintaining the fragment velocity.The results show that through the multi－spot eccentric initiation，the velocity of the directional fragment increases by about 34%，and the directional area range is approximately 30°；the selection criteria of the number of initiation spot is associated with the shell length and the charge diameter.Our study can provide a reference for the engineering application of multi－spot initiation eccentric warhead.

eccentric warhead；Mach reflection；multi－spots eccentric initiation；fragment velocity

O383 國標學科代碼：1303530

A

10.11883／1001－1455（2017）06－1039－07

2016－05－20；

2016－09－18

國家自然科學基金項目（11202103）

沈慧銘（1988— ），男，博士研究生，shenhuiming202＠163.com。

（責任編輯 王易難）