基于J－C模型的鎂合金MB2動靜態拉伸破壞行為＊

賈 東，黃西成，胡文軍，張方舉

基于J－C模型的鎂合金MB2動靜態拉伸破壞行為＊

賈 東，黃西成，胡文軍，張方舉

（中國工程物理研究院總體工程研究所，四川 綿陽621999）

為了研究不同應力狀態和應變率條件下鎂合金MB2的拉伸破壞行為，利用材料試驗機和分離式Hopkinson拉桿（SHTB），對鎂合金MB2的光滑及缺口圓柱試件進行了動靜態拉伸加載；擬合得到了鎂合金MB2的動靜態拉伸本構關系，建立了其修正的Johnson－Cook失效破壞準則，并對不同試件的拉伸破壞行為進行了數值模擬；利用SEM對宏觀破壞模式對應的微觀損傷機理進行了分析。結果表明，隨著應力三軸度的增加，鎂合金MB2的等效破壞應變先增大后減小，宏觀破壞模式由剪切轉為正拉斷，微觀損傷機制由混合斷裂轉變為韌窩斷裂；而隨著應變率的增加，等效破壞應變不斷減小，破壞模式不發生改變。Johnson－Cook本構關系和修正后的Johnson－Cook失效破壞準則能較好地擬合動態靜態拉伸實驗結果并預測不同試件的杯錐形破壞特征。

破壞行為；SHTB實驗；鎂合金MB2；應力三軸度；應變率

鎂合金是一種潛力巨大的輕質工程材料，有著廣闊的應用前景，其中MB2是鎂合金的典型代表。材料在復雜應力狀態下的失效破壞行為是工程材料和結構設計的理論基礎。目前，鎂合金在動靜態加載下的力學行為研究以單向應力狀態為主［1－3］，且能實現復雜應力動態加載的實驗設備與技術尚不成熟。J.W.Hancock等［4］研究發現金屬的延性明顯依賴于應力的三軸狀態。近年來，O.S.Hopperstad等［5－6］對結構鋼進行了拉伸加載實驗和數值分析，結果表明材料的等效破壞應變隨應力三軸狀態的變化趨勢與J.W.Hancock等的研究結論一致；Y.B.Bao［7］在單軸加載條件下對鋁合金2024進行了不同應力狀態的實驗研究；D.Anderson等［8］研究了應力三軸度和應變率對DP780鋼破壞行為的影響。湯安民等［9］、李智慧等［10］研究了不同金屬材料宏觀斷裂形式及斷裂機理與應力狀態的關系，陳剛等［11］建立了應力三軸度和應變率相關的45鋼損傷失效模型，朱浩等［12］分析了應力三軸度和應變率對鋁合金6063力學性能的影響，張偉等［13］以應力三軸度和應變率效應為基礎給出了鋁合金7A04的本構關系和失效模型。

所以，對于鋼材、鋁合金等常用金屬材料，其失效破壞行為的研究已經很多，而對鎂合金復雜應力狀態下的失效破壞行為研究還很少。本文中將通過復雜應力下的動靜態拉伸實驗及數值模擬，分析應力狀態和應變率對鎂合金MB2失效破壞的影響，基于Johnson－Cook本構及失效模型建立適用于鎂合金MB2的破壞準則，分析其宏觀破壞模式及其微觀失效機理，為鎂合金MB2在實際工程中的應用提供強度設計依據和理論支撐。

1 動靜態拉伸實驗方法

材料所受應力狀態不同時，材料內產生的塑性變形與應力集中程度將不同，為了表征材料的復雜應力狀態，引用應力三軸度η為應力狀態參數，即平均應力與等效應力的比值σH／σ－。在延性金屬復雜應力狀態的失效破壞研究中，依據Bridgman原理［14］設計的缺口試件拉伸實驗是最主要的研究方法，根據圓弧缺口頸部應力方程解，可以得到應力三軸度的計算公式：

式中：a和R分別為最小橫截面的半徑及缺口半徑，r為到橫截面中心的距離，a0為最小橫截面初始半徑。基于塑性不可壓的假設，可以得到缺口處的等效應變定義公式如下：

當a取試件斷裂時的橫截面直徑af時，式（2）計算得到的即為試件的等效破壞應變ε－f。靜態拉伸實驗試件采用直徑為5mm的光滑圓柱以及最小橫截面直徑為6mm，缺口曲率半徑分別為9、6、3mm的缺口圓柱試件。動態拉伸實驗試件采用直徑為3mm的光滑圓柱以及最小橫截面直徑為2mm，缺口曲率半徑分別為1.0、1.5、2.0、3.0mm 的缺口圓柱試件。靜態拉伸加載由材料試驗機 MTS 810完成，而動態拉伸加載則通過分離式Hopkinson拉桿（SHTB）實驗裝置完成，如圖1所示。

圖1 SHTB實驗系統Fig.1SHTB testing system

2 鎂合金MB2的動靜態本構關系

2.1 應變率及絕熱效應

對于光滑圓柱試件的動態拉伸實驗，按照一維應力波理論進行數據處理分析可知，試件在不同應力幅值的入射波作用下表現出了明顯的應變率效應，不同應變率下的真實應力應變曲線如圖2所示。

在高速沖擊載荷作用下，加載過程為絕熱過程，材料在該過程中的溫度變化ΔT可由塑性變形進行求解：

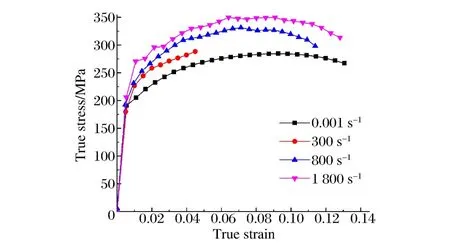
圖2 鎂合金MB2真實應力應變曲線Fig.2True stress－strain curves of magnesium alloy MB2

式中：β為摩擦能量轉換系數，ρ為材料密度，cp為比定壓熱容，εp為等效塑性應變。對于鎂合金 MB2，摩擦能量轉換系數通常取為0.925，密度為1 800kg／m3，比定壓熱容為1 040～1 148J／（kg·K）。

2.2 本構模型參數擬合

鑒于鎂合金MB2的應變率效應，這里引用經典的J－C本構模型對實驗結果進行擬合。在室溫、準靜態（0.001s－1）拉伸條件下，J－C本構模型的應變率項和溫度項均為1，此時材料的本構模型退化為：

采用最小二乘法對參數A、B、n 進行擬合可以得到：A＝192MPa、B＝218.3MPa、n＝0.370 56。由于在300s－1下試件未被拉斷，所以這里以800和1 800s－1應變率下的抗拉強度及其對應的等效塑性應變作為比較點與參考應變率0.001s－1進行比較分析，獲得參數C的算術平均值為0.015。對于反映溫度效應的參數m，由于本研究未涉及高溫下的動態拉伸實驗，所以此處引用文獻［15］中的研究結論，給出參數m的值為0.95。

3 失效破壞行為

3.1 宏觀失效破壞

對于光滑圓柱試件和缺口圓柱試件，由于其加載過程中應力狀態的差異，導致其動靜態加載條件下的破壞形式也有所不同，如圖3所示。

圖3 不同試件破壞模式Fig.3Macro fracture patterns of different specimens

光滑圓柱試件在整體上發生剪切破壞，且在破壞前有一定的頸縮，試件斷口處有一定的杯錐特征。缺口試件在準靜態條件下整體上發生正拉斷，斷口邊緣有杯錐特征；在動態加載下整體表現為杯錐形斷裂。通過測量斷裂后缺口處的最小橫截面直徑，得到了動態拉伸試件不同加載條件下的等效破壞應變，如表1所示。

表1 不同類型試件的等效破壞應變Table 1Equivalent fracture strain of different specimens

3.2 J－C失效模型

J－C失效模型類似于J－C本構模型，采用多項乘積的形式對應力狀態參數、應變率參數以及溫度效應參數進行解耦。由于在本研究中未涉及等效破壞應變的溫度效應，所以此處給出簡化后的表達形式如下：

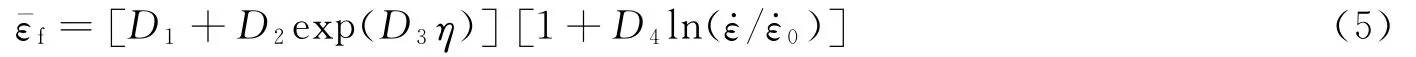
式中：D1、D2、D3、D4為失效模型系數。研究發現，試件最小橫截面處的應力三軸度是隨等效應變的增加而不斷變化的，整個加載過程的應力三軸度計算需要考慮到應變的累積效應［16］，所以D.M.Goto等［17］、Y.Bao等［18］在研究不同延性金屬材料時，對整個加載過程的平均應力三軸度ηav進行了定義：

采用ABAQUS／Explicit分析軟件對鎂合金MB2不同類型試件的動態拉伸實驗過程進行模擬計算，鑒于SHTB和試件的對稱性，以軸對稱單元進行建模，以拉伸本構關系和實驗中采集的入射波為輸入條件，模擬得到了試件在加載過程中應力三軸度的變化情況，如圖4所示。

同時，由于缺口試件動態加載過程中，其塑性變形集中于缺口區域，并不滿足一維應力波原理，無法通過理論公式對應變率進行求解。所以這里根據缺口試件等效應變的定義，借助數值模擬得到最小橫截面直徑的變化和應力波作用時程，通過時間積分得到試件的平均應變率：

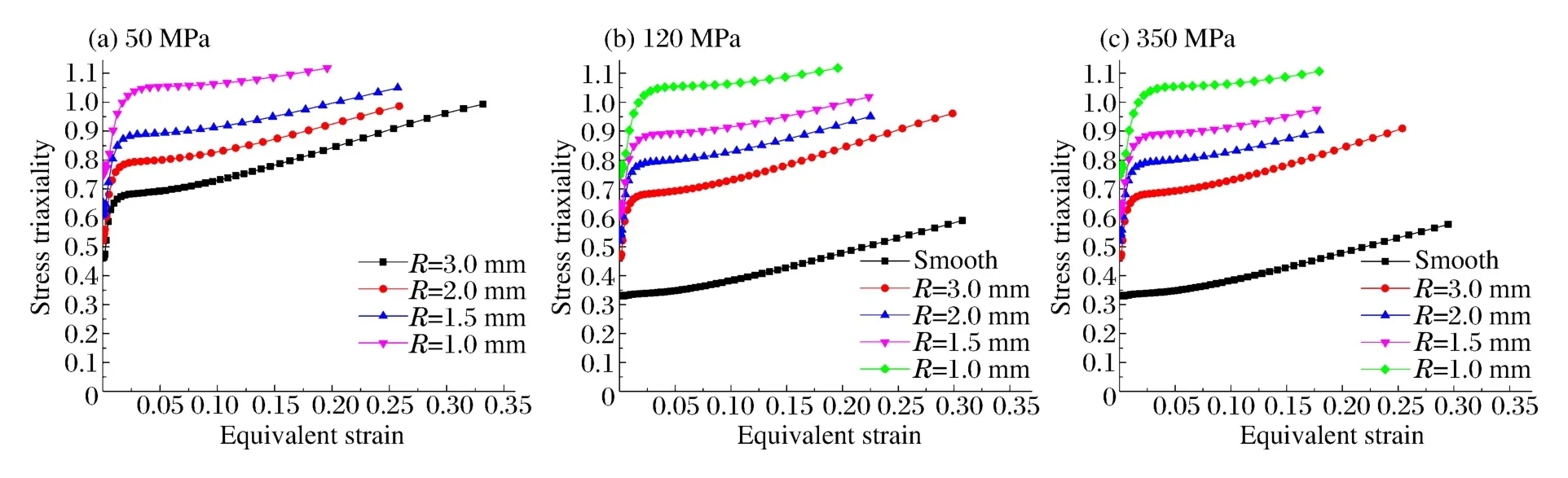
圖4 不同類型試件應力三軸度變化Fig.4Stress triaxiality curves of different specimens

式中：Δt為試件發生拉伸變形的時間，t0為載荷作用開始的時刻，tf為載荷作用結束的時刻。通過數值計算得到不同類型試件入射波在試件上的作用時間，進而計算得到其平均應變率，如表2所示。

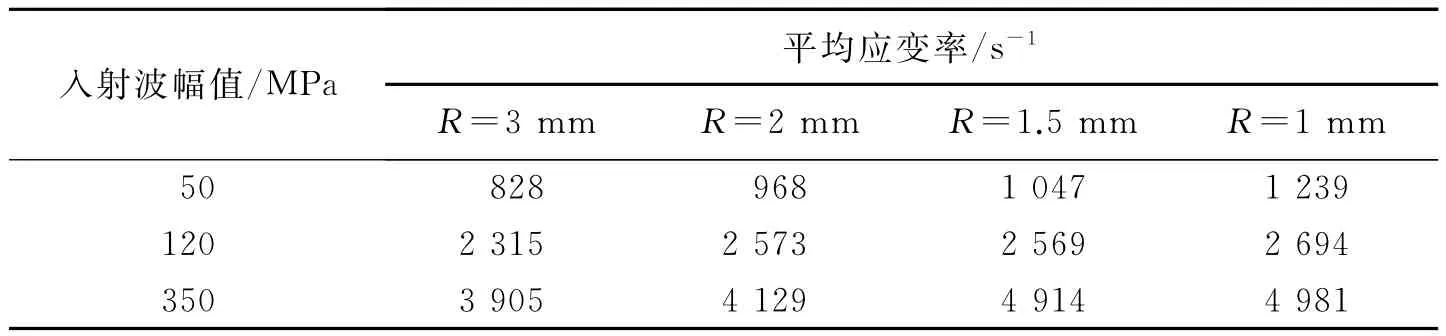
表2 缺口試件的平均應變率Table 2Average strain rates of different specimens

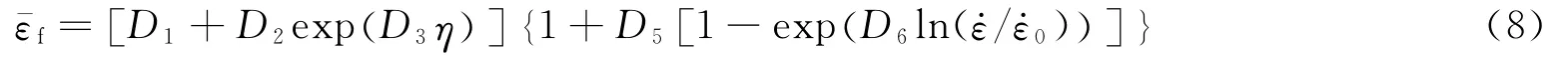
結合參數擬合的結果，可以得到鎂合金MB2最終的破壞準則為以應力三軸度0.66為轉折點的分段函數形式，如圖6所示。圖中實心圓點為實驗結果，曲面為破壞準則的擬合結果。

通過失效破壞曲面可以發現，鎂合金MB2的斷裂延性（等效破壞應變）隨著應力三軸度的增加先增大后減小，隨著應變率的增大而不斷減小。從破壞模式上來看，隨著應力三軸度的增大，材料先發生剪切破壞，隨后又發生正拉斷破壞；隨著應變率的增大，光滑圓柱及缺口圓柱試件在動靜態載荷作用下的破壞形式基本一致。所以，應力狀態對斷裂延性和破壞模式的影響存在明顯的轉折點，而應變率的影響則不存在轉折點。

為了對該失效模型進行驗證，這里通過ABAQUS／Explicit分析軟件和單元失效法對不同類型試件的動態失效破壞形式進行了數值模擬分析，其模擬結果如圖7所示。

從數值模擬結果可以看出，無論是光滑圓柱試件還是缺口圓柱試件，其最終破壞形式均呈現出杯錐形特征，這與實驗現象是基本吻合的；但對于光滑圓柱試件，該模型不能體現試件的整體剪切斷裂特征，這與J－C失效模型的物理涵義以及鎂合金MB2在不同應力狀態下的微觀損傷機理有關。

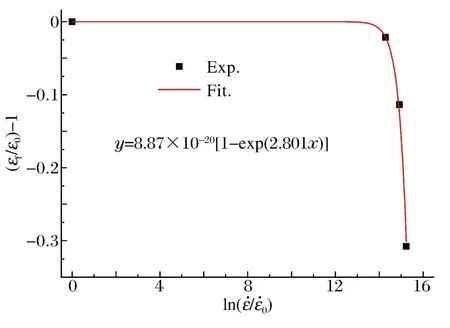
圖5 應變率項參數擬合曲線Fig.5Fitted curve for the item of strain rates

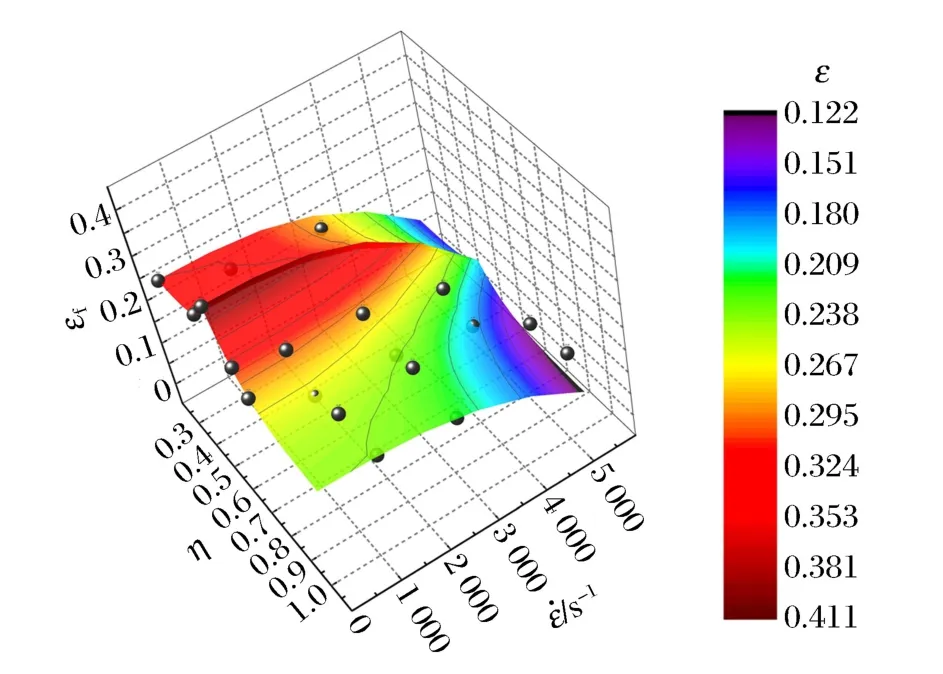
圖6 鎂合金MB2的破壞準則曲面Fig.6Fracture criterion surface of magnesium alloy MB2

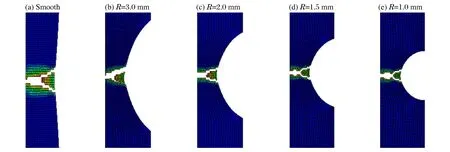
圖7 不同試件失效破壞模式的數值模擬結果Fig.7Fracture patterns of different specimens from numerical simulation

3.3 微觀失效機理

宏觀破壞行為與材料的微觀損傷變形機制密切相關，為進一步認識應力狀態對鎂合金MB2破壞行為的影響，對準靜態條件下光滑圓柱及缺口試件的斷口形貌進行微觀掃描觀察，如圖8所示。

圖8 試件微觀斷口形貌Fig.8Micro fracture morphology of specimens

對于光滑拉伸試件，微觀斷口上能看到河流花樣特征即解理斷裂，同時也呈現出了一定的微孔洞特征，即有韌性斷裂的特點，如圖8（a）所示，屬韌脆性混合斷裂；對于缺口試件，不同缺口程度均表現出較明顯的微孔洞斷裂的特征，在圖8（b）中能清晰地看到韌窩聚合、連接的特點。這些特征與試件在宏觀破壞形式上的表現是一致的，即光滑圓柱試件破壞是由混合損傷機制引起的，而缺口試件破壞則是由微孔洞損傷演化機制決定的。J－C失效模型在微觀上反映的是材料的微孔洞損傷演化機理，在宏觀上體現為該微觀損傷機理導致的材料斷裂延性變化，不能體現其他變形機制的作用，這就是模擬結果可以描述光滑圓柱試件的杯錐形破壞特點而無法描述其整體剪切特征的原因。

4 結 論

（1）通過缺口圓柱試件設計能夠實現鎂合金MB2不同程度的多向應力狀態，結合SHTB裝置可以實現其在復雜應力狀態下的動態拉伸加載研究。

（2）在研究的實驗條件范圍內，應力狀態對鎂合金MB2破壞行為的影響存在明顯的轉折點，而應變率（5 000s－1以內）則不存在轉折點。通過模型修正和參數擬合得到了鎂合金MB2的等效破壞應變準則，且其數值模擬結果可以較好地體現拉伸試件的杯錐形破壞特征。

（3）鎂合金MB2不同應力狀態下的破壞行為與其微觀損傷機理密切相關，隨著應力三軸度的增加，其微觀損傷機制由混合斷裂轉變為韌窩斷裂，這是導致其宏觀延性和破壞模式發生變化的重要原因。

［1］ 胡昌明，李英雷，胡時勝，等.高溫－高應變率下 MB2合金的動態力學性能及變形機理［J］.兵器材料科學與工程，2009，32（5）：8－11.Hu Changming，Li Yinglei，Hu Shisheng，et al.Dynamic mechanical properties and deformation mechanism of MB2ally under high temperature and high strain rates［J］.Ordnance Material Science and Engineering，2009，32（5）：8－11.

［2］ Zhao Feng，Li Yulong，Suo Tao，et al.Compressive deformation behavior of AZ31magnesium alloy under quasistatic and dynamic loading［J］.Transactions of Nonferrous Metals Society of China，2010，20（7）：1316－1320.

［3］ 劉正，董陽，毛萍莉，等.軋制 AZ31鎂合金板材（4mm）動態壓縮性能與失效行為［J］.材料工程，2015，43（2）：61－66.Liu Zheng，Dong Yang，Mao Pingli，et al.Dynamic compressive properties and failure behaviour of rolled AZ31 magnesium alloy sheet（4mm）［J］.Journal of Materials Engineering，2015，43（2）：61－66.

［4］ Hancock J W，Mackenzie A C.On the mechanisms of ductile failure in high strength steels subjected to multi axial stress states［J］.Journal of the Mechanics and Physics of Solids，1976，24（2）：147－160.

［5］ Hopperstad O S，B?rvika T，Langseth M，et al.On the influence of stress triaxiality and strain rate on the behaviour of a structural steel.PartⅠ.Experiments［J］.European Journal of Mechanics，2003，22（1）：1－13.

［6］ B?rvik T，Hopperstad O S，Berstada T.On the influence of stress triaxiality and strain rate on the behaviour of a structural steel.PartⅡ.Numerical study［J］.European Journal of Mechanics，2003，22（1）：15－32.

［7］ Bao Y B.Dependence of ductile crack formation in tensile tests on stress triaxiality，stress and strain ratios［J］.Engineering Fracture Mechanics，2005，72（4）：505－522.

［8］ Anderson D，Winkler S，Bardelcik A，et al.Influence of stress triaxiality and strain rate on the failure behavior of a dual－phase DP780steel［J］.Materials and Design，2014，60（8）：198－207.

［9］ 湯安民，師俊平.幾種金屬材料宏觀斷裂形式的試驗研究［J］.應用力學學報，2004，21（3）：142－144.Tang Anmin，Shi Junping.Experiment analysis of macroscopic fracture forms for several metal materials［J］.Journal of Applied Mechanics，2004，21（3）：142－144.

［10］ 李智慧，師俊平，湯安民.金屬材料脆性斷裂機理的實驗研究［J］.應用力學學報，2012，29（1）：48－53.Li Zhihui，Shi Junping，Tang Anmin.Experimental research on the brittle fracture mechnism in metal material［J］.Journal of Applied Mechanics，2012，29（1）：48－53.

［11］ 陳剛，陳忠富，徐偉芳，等.45鋼的J－C損傷失效參量研究［J］.爆炸與沖擊，2007，27（2）：131－135.Chen Gang，Chen Zhongfu，Xu Weifang，et al.Investigation on the J－C ductile fracture parameters of 45steel［J］.Explosion and Shock Waves，2007，27（2）：131－135.

［12］ 朱浩，朱亮，陳劍虹.應力三軸度和應變率對6063鋁合金力學性能的影響及材料表征［J］.材料科學與工程學報，2007，25（30）：358－362.Zhu Hao，Zhu Liang，Chen Jianhong.Influence of stress triaxiality and strain rate on the mechanics behavior of 6063aluminum ally and material characterization［J］.Journal of Materials Science and Engineering，2007，25（30）：358－362.

［13］ 張偉，肖新科，魏剛.7A04鋁合金的本構關系和失效模型［J］.爆炸與沖擊，2011，31（1）：81－87.Zhang Wei，Xiao Xinke，Wei Gang.Constitutive relation and fracture model of 7A04aluminum alloy［J］.Explosion and Shock Waves，2011，31（1）：81－87.

［14］ Bridgman P W.Studies in large plastic flow and fracture with special emphasis on the effects of hydrostatic pressure［M］.New York：McGraw Hill，1952.

［15］ Feng Fei，Huang Shangyu，Meng Zhenghua，et al.A constitutive and fracture model for AZ31Bmagnesium alloy in the tensile state［J］.Materials Science and Engineering A，2014，594（4）：334－343.

［16］ Alves M，Jones N.Influence of hydrostatic stress on failure of axisymmetric notched specimens［J］.Journal of the Mechanics and Physics of Solids，1999，47（3）：643－667.

［17］ Goto D M，Koss D A，Jablokov V.The influence of tensile stress states on the failure of HY－100steel［J］.Metallurgical and Materials Transactions A，1999，30（11）：2835－2842.

［18］ Bao Y B，Wierzbicki T.On fracture locus in the equivalent strain and stress triaxiality space［J］.International Journal of Mechanical Sciences，2004，46（1）：81－98.

［19］ 賈東，莫軍，黃西成，等.鎂合金 MB2在高應力三軸度下的拉伸破壞行為研究［J］.實驗力學，2016，31（1）：87－95.Jia Dong，Mo Jun，Huang Xicheng，et al.On the fracture behavior of magnesium alloy MB2subjected to high stress triaxiality stretching［J］.Journal of Experimental Mechanics，2016，31（1）：87－95.

Fracture behavior of magnesium alloy MB2under quasi－static and dynamic tension loading based on Johnson－Cook model

Jia Dong，Huang Xicheng，Hu Wenjun，Zhang Fangju
（Institute of Systems Engineering，China Academy of Engineering Physics，Mianyang621999，Sichuan，China）

In the present study，we loaded smooth and notched cylindrical specimens of magnesium alloy MB2under quasi－static and dynamic tension states using the material testing machine and split Hopkinson tension bar（SHTB），to characterize the alloy’s tensile fracture behaviors under different stress states and strain rates.The constitution of the alloy for quasi－static and dynamic tension states was fitted and the modified fracture criterion based on the Johnson－Cook model was established and then used to simulate the fracture behavior of different tensile specimens.The microscopic damage mechanisms corresponding to the macroscopic fracture pattern was analyzed by SEM.The results show that with the increase of the stress triaxiality，the equivalent strain to fracture of the alloy increases at first and then decreases，and the fracture pattern changes from shear fracture to vertical tension fracture with micro damage mechanisms changing from the mixed failure to the dimple failure；with the increase of the strain rate，the equivalent strain to fracture decreases，and the fracture pattern remains the same.The Johnson－Cook constitution and the modified Johnson－Cook fracture criterion can be used to fit the experimental results under quasi－static and dynamic tension states and predict the cup－cone fracture characteristics of different specimens.

fracture behavior；SHTB experiment；magnesium alloy MB2；stress triaxiality；strain rate

O346.1 國標學科代碼：13015

A

10.11883／1001－1455（2017）06－1010－07

2016－04－12；

2016－11－27

國家自然科學基金項目（11472257）；中國工程物理研究院總體工程研究所創新與發展基金項目（13CXJ09）

賈 東（1986— ），男，碩士，助理研究員，jiadong＠mail.ustc.edu.cn。

（責任編輯 曾月蓉）