提高弱電網中光伏并網逆變器穩定性的控制方法*

孫如田，鄭松

（1.克拉瑪依職業技術學院，新疆獨山子833600；2.杭州電子科技大學，杭州310018）

0 引 言

隨著傳統化石能源的大量消耗以及環境問題的惡化，近年來以風光為代表的新能源倍受人們的青睞，大量的分布式電源接入電網之中［1-2］。隨著電網中新能源滲透率的增大，電網越來越表現出弱電網的特性［2-3］。弱電網中電網阻抗的變化會導致系統穩定裕度降低，使系統進入不穩定運行狀態，尤其是對于多逆變器并聯系統，可能導致逆變器之間的不穩定現象，威脅著系統的安全穩定運行［4-5］。

目前已有部分文獻提出了增強弱電網中并網逆變器穩定性的方法，文獻［3］采用虛擬阻抗技術對逆變器輸出阻抗進行改善，進而提高并網逆變器對電網阻抗變化的適應性，但該方法在實現過程中需要引入微分環節，工程實際中不能實現；文獻［6］針對多逆變器并網系統提出在并網點添加一個阻性有源濾波器來增強系統的穩定性，但該方法需要額外添加硬件設備，提高了成本。文獻［7］采用零補償的控制策略來提高系統的相位裕度，但當電網阻抗大范圍變化時，該方法的效果較差；文獻［8］采用在濾波電感L1和電容C支路串聯或者并聯虛擬電阻的方法來改善逆變器的等效輸出阻抗，但該方法在改變輸出阻抗的同時也改變了電流環的性能。

基于上述分析，本文首先分析了電網阻抗變化對系統無源阻尼比及穩定性能的影響，然后提出一種變增益控制策略來對系統的相位進行實時補償，進而提高系統的穩定性，增強系統對電網的適應能力。最后通過仿真驗證了本文理論分析的正確性。

1 電網中并網逆變器穩定性分析

1.1 并網逆變器等效模型

圖1為一種常見的并網逆變器控制結構，其中icabc、isabc、upabc分別為濾波器三相電容電流、三相并網電流及三相并網點電壓。Zg為電網阻抗，主要包括電阻和電抗，系統的穩定性問題由感性分量引起［9-10］，因此本文只考慮感性分量，記 Zg（s）＝sLg。由于在三相靜止坐標系下無法實現有功和無功的解耦控制，因此將系統轉換到兩相靜止坐標系下進行控制，kc為電容電流有源阻尼系數。

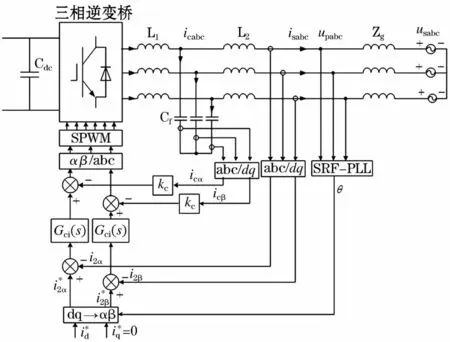
圖1 三相并網逆變器及其控制結構Fig.1 Control strategy of the grid-connected inverter in two-phase stationary coordinate system

采用對正弦交流能夠實現無靜差跟蹤的準PR控制器來控制并網電流，其數學模型如式（1）所示［9］。

工程實際應用中，電網阻抗可以認為是濾波電感L2的一部分。因此可以得到系統在復頻域下的等效控制結構如圖2所示（僅以a軸為例進行分析）。忽略系統擾動usa（s），則可以得到參考電流到輸出并網電流的開環傳遞函數如式（2）所示。

圖2 系統控制結構模型Fig.2 Control configuration model of the system

式中 Leq＝L2+Lg

1.2 電網阻抗對系統穩定性的影響

為了抑制高頻諧波，系統的開環截止頻率ωc一般設置得遠小于開關頻率ωs，而濾波電容對系統低頻特性的影響較小，因此在ωc處可以忽略濾波電容的影響，將jωc帶入式（2）得到系統開環傳遞函數在截止頻率處的幅值：

對于準PR控制器，雖然在極點頻率ω0處能夠獲得很大的幅值增益，但在該頻率處系統的相頻曲線穿越0°線，對系統相位造成了-180°的相移。為了減小控制器對系統相位裕度的影響，通常將ωc設計得遠大于ω0。故在ωc處可以將準PR控制器近似簡化為：

將 Gc（jωc）代入式（3），由開環傳遞函數在截止頻率處的幅值為1得到：

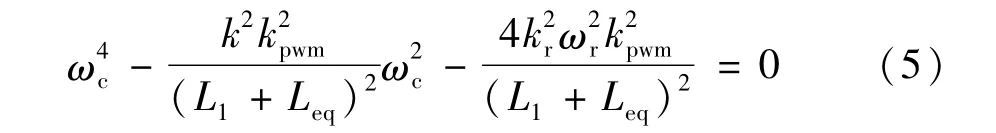
由式（5）可以解得 ωc，然后將 jωc代入式（1）可得準PR控制器在ωc處的相角：

根據式（2）得到不考慮準PR控制器時電流開環傳遞函數在截止頻率ωc處的相角：

因此可以得到系統的相位裕度為［7］：

以表1中所示的逆變器參數為例，根據式（6）可以得到系統相位裕度隨電網阻抗變化的曲線如圖3所示。可以看出隨著電網的增加，系統相位裕度減小。當電網增加到一定值時，系統相位減小至零。當電網阻抗繼續增大時，相位進一步減小為負值，系統出現不穩定現象。

表1 系統參數Tab.1 System parameters

圖3 系統相位裕度隨電網阻抗變化曲線Fig.3 Curve of phasemargin with grid impedance variation

2 提高弱電網中并網逆變器穩定性的控制方法

上述分析表明弱電網中電網阻抗的變化會使系統的相位裕度降低，導致系統進入不穩定狀態。如果能夠在電網阻抗變化的過程中維持系統具有足夠的相位裕度，則可以保證系統具有足夠的穩定裕度，進而可以避免不穩定現象的發生。因此本文提出一種變增益的控制方法來實時補償系統的相位裕度，進而增強系統的穩定性。

首先采用如式（7）所示的環節對系統的開環相位進行補償，其能夠對特定頻率處的相位進行補償，且對系統開環增益幾乎無影響［2，11］。

式中k1、k2和k3均為系統的調節參數，可以通過調節這兩個參數來改變系統的相位及幅值。

采用所提環節補償后的電流環控制器為：

系統相位曲線變化情況如圖4所示，可以看出隨著電網阻抗的增加，系統相位趨于恒定。

圖4 開環傳遞函數相位曲線Fig.4 Phase curve of open loop transfer function

由圖4可以看出，經式（7）所示環節補償后每一個電網阻抗值所對應的系統開環相位曲線在基波頻率ω0至相位交界頻率ωg范圍內均存在一個峰值。如果通過調節系統增益的方法使得開環截止頻率始終在上述相位峰值所對應的頻率點ωp處取得，則系統將始終具有足夠的相位裕度。根據運行條件對比例系數k1進行實時調整，進而使系統的相位裕度達到最大值。系統的可變增益控制結構如圖5所示。

圖5 變增益控制結構框圖Fig.5 Block diagram of gain-scheduling control configuration of the system

3 徑向基函數（Radial Basis Function，RBF）神經網絡

徑向基函數神經元網絡是一種前向網絡，其拓撲結構如圖6所示。這種網絡完成如式（8）所示的非線性映射［12］：

式中 X∈Rn是輸入矢量；ψ（·）是一個R+→R的函數；｜｜·｜｜是歐氏范數；Wi是權值；ci是 RBF網絡的數據中心；nr是中心數目。ψ（·）取徑向基函數主要基于如下原理。

圖6 RBF神經網絡結構Fig.6 Structure of the RBF neural network

如果前向學習集合為 S＝｛（Xi，ti）∈Rn×R｜i＝1…N｝，ψ（·，W）是未知函數，W是待學習的權值，那么神經網絡學習過程就是尋找ψ（·，W）及W使式（9）中的能量函數取最小值：

式中｜｜·｜｜是函數空間上的 L2范數，約束算子 P（·）應當仔細選擇以保證函數ψ的平滑。λ表示約束的嚴格程度。從正則方法出發采用變分原理可以證明ψ（·）應該取徑向基函數。

容易看出，k1是關于電網阻抗Lg的非線性函數，直接根據系統模型求解該非線性函數是非常困難的，因此本文采用徑向基函數（Radial Basis Function，RBF）神經網絡對該非線性函數進行建模，具體步驟如下：

（1）在［0mH，5mH］內隨機取一列數值作為Lg的輸入值，然后根據系統模型采用數值計算的方法求取每一個電網阻抗值所對應的kx值；

（2）將步驟（1）所得的數據組分為兩部分，其中一部分用來訓練神經網絡模型，另外一部分用來對訓練好的模型進行驗證。

對訓練好的RBF神經網絡模型進行驗證的結果如圖7所示，可以看出由神經網絡模型的數據與實際

圖7 神經網絡模型輸出結果Fig.7 Output result of neural network

數據幾乎完全重合，因此所訓練的RBF神經網絡模型可以用來代替k1關于Lg的非線性函數。

3 變增益控制方法對電網阻抗的魯棒性分析

采用變增益控制方法后系統相位裕度隨電網阻抗的變化曲線如圖8所示，可以看出隨著電網阻抗的增加系統始終具有足夠的相位裕度，滿足系統穩定性的要求。圖9進一步給出了不同電網阻抗情況下開環傳遞函數伯德圖，可以看出隨著電網阻抗的增加系統開環截止頻率有所降低，但始終遠大于基波頻率，且在基波頻率處始終具有足夠大的幅值增益，滿足跟蹤性能的要求。

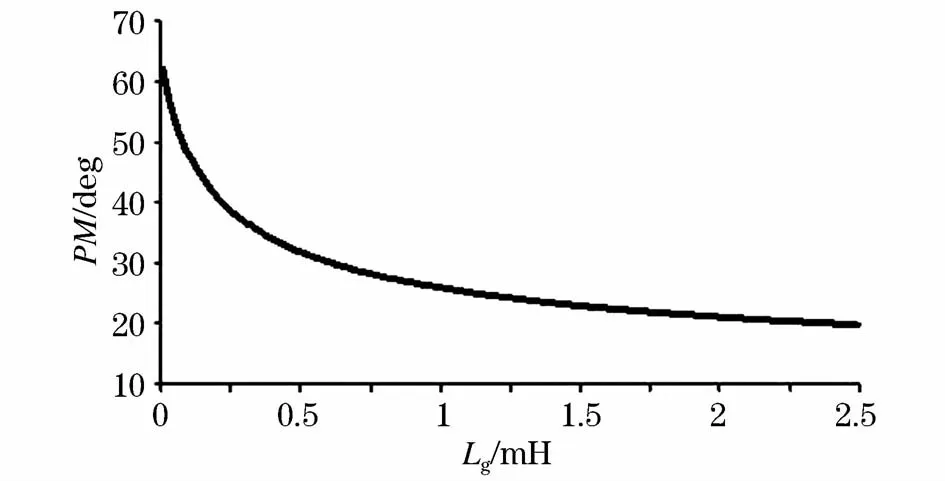
圖8 采用變增益控制方法后相位裕度隨電網阻抗變化曲線Fig.8 Stabilitymargin curve with grid impedance variation after adopting varying-gain control strategy

圖9 采用變增益控制方法后系統開環傳遞函數伯德圖Fig.9 Bode diagram of open loop transfer function after adopting varying-gain control strategy

4 仿真驗證

為了驗證理論分析的正確性，以一臺額定容量為250 kW的逆變器為例進行仿真分析，仿真系統主要參數如表1所示。電網采用三相交流理想電壓源模擬，電網阻抗采用集中參數電感模擬，光伏電池采用文獻［13］中的數學模型搭建。

圖10為原始系統相位裕度為零情況下（Lg＝1.25 mH），采用本文所提可變增益控制方法前后系統仿真波形。可以看出在采用可變增益控制方法之前，由于系統相位裕度接近于零，因此系統處于臨界不穩定狀態，并網電流中諧波含量較大，波形畸變嚴重。加入本文所提控制方法后，并網點電壓及并網電流波形均變好，滿足并網要求，系統處于穩定運行狀態。

圖10 L g＝1.25 mH時采用變增益控制方法前后仿真波形Fig.10 Simulation waveform before and after adopting varying-gain control strategy under 1.25 mH grid impedance

圖11、圖12為原始系統相位裕度為負值情況下（Lg＝2 mH，Lg＝3 mH），采用本文所提出的可變增益控制方法前后系統仿真波形。可以看出由于原始系統的相位裕度為負值，采用本文所提控制方法前并網電流及并網點電壓均畸變嚴重，系統處于不穩定運行狀態。當加入所提控制方法后，兩種情況下系統并網電流及并網點電壓均變好，諧波含量較小，滿足并網要求，系統處于穩定運行狀態。

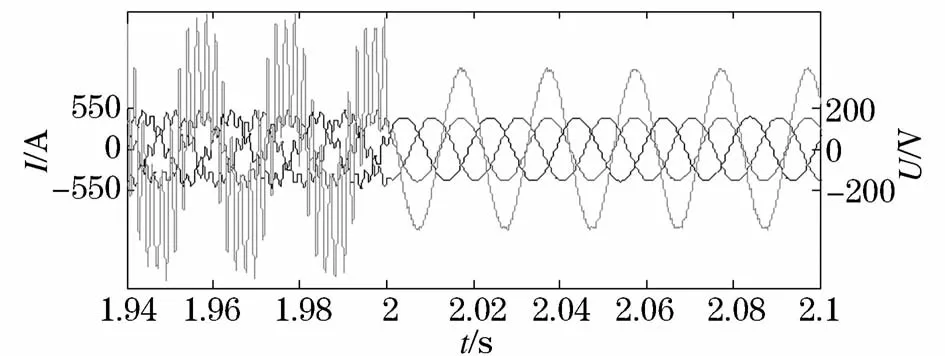
圖11 L g＝2 mH時采用變增益控制方法前后仿真波形Fig.11 Simulation waveform before and after adopting varying-gain control strategy under 2 mH grid impedance

綜上所述：不論原始系統的相位裕度為零，還是為負值，當加入本文所提可變增益控制方法后，系統穩定裕度得到提高，并網電流及并網點電壓波形良好，滿足并網要求。

圖12 L g＝3 mH時采用變增益控制方法前后仿真波形Fig.12 Simulation waveform before and after adopting varying-gain control strategy under 3 mH grid impedance

5 結束語

文章研究了電網阻抗對并網逆變器穩定性的影響，電網阻抗的增加導致系統穩定裕度降低，從而使系統進入不穩定狀態。提出了一種基于神經網絡的變增益控制方法對系統相位裕度進行實時補償，從而實現系統穩定裕度的提升。在電網阻抗變化的過程中，變增益控制方法能夠始終維持系統具有足夠的穩定裕度，提高了系統穩定性，增強了系統對電網阻抗變化的魯棒性。