基于模糊聚類與隨機森林的短期負荷預測*

黃青平，李玉嬌，劉松，劉鵬

（華北電力大學電氣與電子工程學院，北京102206）

0 引 言

電力系統短期負荷預測是電力部門非常重要的工作之一，它影響整個系統的調度、發電和電能存儲的方案制定和實施。長期以來如何提高負荷預測的精度是國內外學者一直致力研究的目標，負荷預測精度會直接影響電網運行的資金和安全［1-2］，因此提出可行性好、精度較高的負荷預測方法具有非常重要的意義。

目前，負荷預測方法主要劃分成兩種：傳統方法和智能預測方法［3］。傳統預測方法主要有時間序列法［4］、回歸方法［5］和指數平滑法［6］。時間序列法對不定性的因素如溫度、濕度考慮不充分，當天氣發生驟變時，預測誤差較大。線性回歸方法形式簡單但處理非線性能力差，預測精度低。指數平滑法基于“近大遠小”理論，采用歷史負荷進行加權平均，即越近的負荷加權系數越大，但該方法仍然不能反映日期、氣象等因素與負荷的非線性關系。近年來，基于智能原理的負荷預測方法得到了廣泛應用［7-10］，特別是神經網絡和支持向量機。神經網絡克服了傳統方法不能自主學習以及影響因素考慮不全面等問題，但缺點也較明顯：容易陷入局部最優，隱藏層單元數目難以確定等。SVM預測方法很好的保證全局最優，但其核函數確定困難且模型構建存在較多的人為因素，不利于預測精度的提高。

RF是數據挖掘中重要的分類回歸算法，由多棵決策樹組合成分類器，具有泛化能力強、所需調節參數少和預測精度高等優點，被應用于多個領域［11］。但RF回歸算法應用于負荷預測的文獻較少［12-13］，且傳統負荷預測方法以及智能預測方法（ANN和SVM）自身的局限性大，已經不能滿足預測精度的需求。于是本文考慮將RF回歸方法應用于短期負荷預測，并結合模糊聚類技術，提出一種模糊聚類與隨機森林結合的負荷預測方法。該方法首先依據模糊聚類原理分析，根據樣本相似性選取訓練樣本；然后利用隨機森林算法建立預測模型；最后應用真實的負荷數據驗證該方法的有效性。

1 C均值模糊聚類算法

1973年，Bezdek將早期的模糊聚類進行推廣，提出了C均值模糊聚類［14］，它是利用隸屬度來確定每一個樣本數據屬于某一類的聚類算法。鑒于電力負荷具有周期性變化特性，選擇氣象、日期等負荷影響因子作為聚類的狀態特征變量，與待預測日影響因子相似性高的同類特征數據作為隨機森林訓練樣本的輸入，保證了數據的統一性和相似性。

設 A＝｛A1，A2，…，An｝為預測日的樣本集合，每個樣本xi有m個特征屬性，那么預測樣本xi可表示xi＝｛xi1，xi2，…，xim｝T，（i＝1，2，…，n），C均值模糊聚類是將數據集A劃分為c類，得到c個子集A1，A2，…，Ac滿足：

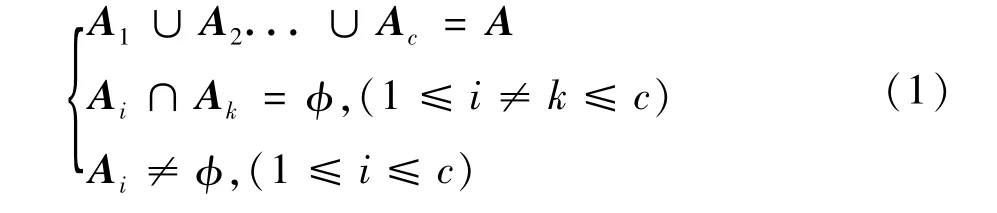
數據樣本 xi屬于 Ak（1≤k≤c）的隸屬度為 Uki，滿足：

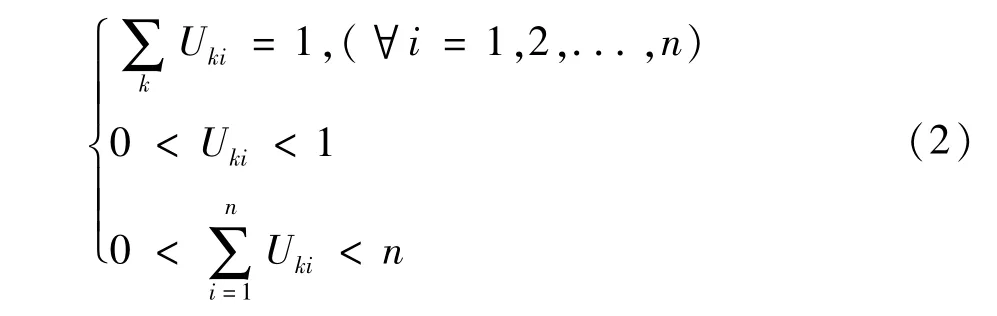
則有目標函數成立：

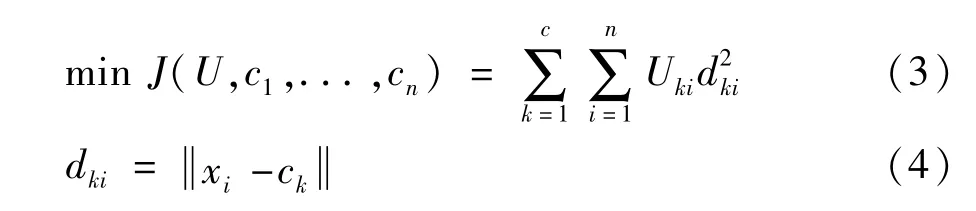
式中dki是第i個樣本到第k類的中心距離；ck是第k類的聚類中心。

C均值模糊聚類算法的目的是要取目標函數的最小值，目標函數最小的兩個必要約束條件為：

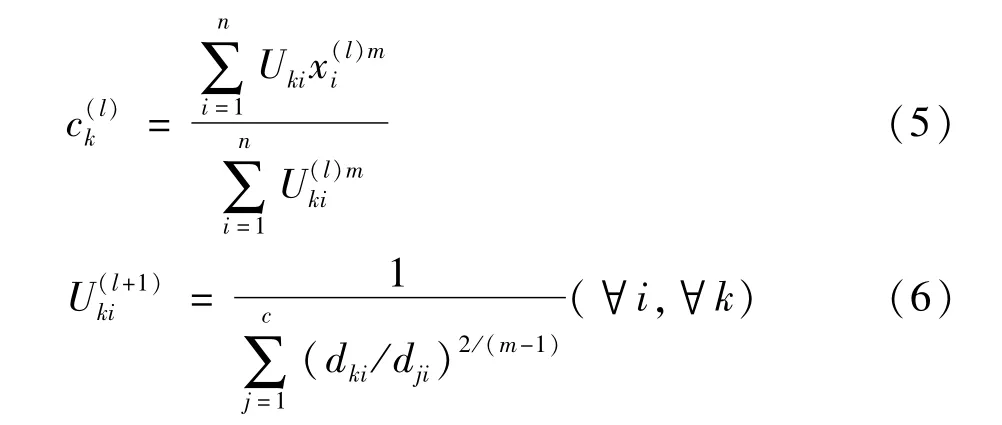
式中m為隸屬度的加權系數。

該算法的基本流程為：

（1）給定兩個基本的參數m和c，一般m取2，計算出初始聚類中心；

（2）初始化隸屬矩陣U；

（4）設置隸屬度最小變化量ε，迭代終止條件，否則l＝l＋1并跳回步驟3執行。

首先將樣本進行分類，設待預測樣本xb＝｛xb1，xb2，…，xbm｝T，然后計算待預測點與各樣本類別的隸屬度函數，將最大隸屬度所對應的類別作為待預測點所屬類別，最后利用類別對應的樣本作為隨機森林的訓練樣本進行負荷預測。

2 隨機森林的基本理論

隨機森林算法是美國科學家LeoBreiman結合bagging集成學習和隨機屬性子空間理論提出的有監督學習算法［15］。該算法通過bootsrap重抽樣方法對原始樣本進行抽樣，每個抽樣樣本的容量與原始樣本一樣；每個bootsrap抽樣的樣本進行CART（分類回歸）決策樹建模；最后組合的多棵CART決策樹作為隨機森林，森林中每棵決策樹投票結果則是最終的預測結果。

2.1 CART決策樹

20世紀70年代后期和20世紀80年代初期，Quinlan提出了ID3決策樹算法［16］，后期將ID3決策樹算法改進提出C4.5決策樹算法；1984年，Breiman等多位統計學家提出了CART決策樹算法，CART是一種二分遞歸分割技術，每個非葉結點被劃分為兩個葉子節點。這三種算法都是采用自頂向下的貪心方法構造決策樹，不同的是屬性選擇度量。每棵決策樹在生長過程中，需要選擇某個屬性作為分裂節點，選擇最優的屬性進行分裂的依據是屬性選擇度量，決定了節點屬性分裂情況。其中ID3決策樹算法使用信息增益作為屬性選擇度量，C4.5決策樹算法選用增益率作為屬性選擇度量，CART決策樹算法利用基尼指數作為屬性選擇度量，CART決策樹算法利用基尼指數作為分類樹的屬性選擇度量；最小二乘偏差作為回歸樹的屬性度量。

（1）CART分類樹的度量屬性

設數據集D中有n個不同的類別Ci，Ci，D是數據集D中Ci類元組的集合，和和分別是D和Ci，D元組的個數，則CART決策樹使用基尼指數Gini（D）計算公式為：

式中 Pi為 Ci類元組出現的頻率，用進行估計。

基尼指數需要考慮每個屬性的二元劃分，若屬性A是離散值，A的二元劃分將D劃分為D1和D2，則在給定劃分的條件下，D的基尼指數為：

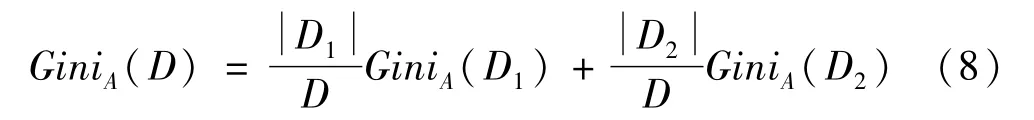
屬性A的二元劃分導致的不純度降低為：

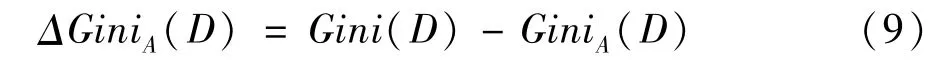
考慮每個屬性可能的二元劃分情況，選擇該屬性產生最大化不純度降低（具有最小基尼指數）的子集作為它的分裂子集。即屬性A的ΔGiniA（D）越大，GiniA（D）越小，在A上的分裂效果越好。

（2）CART回歸樹的度量屬性

分裂節點利用最小二乘偏差作為衡量回歸樹的最優分裂屬性。利用最小二乘偏差計算節點的屬性的劃分公式為：

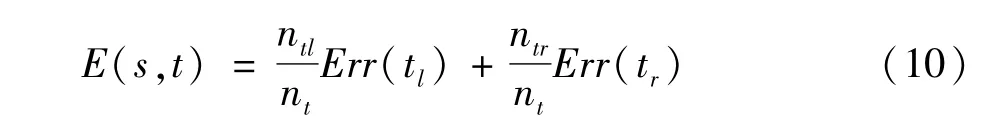
式中t是節點；s為屬性值；nt是節點個數。Errt（t）為節點的誤差其計算公式為：

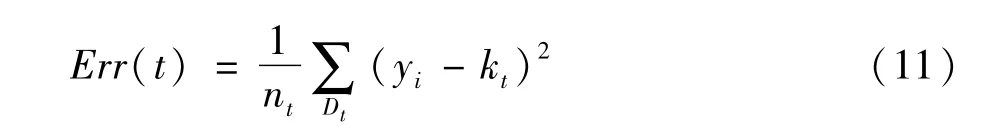
劃分的標準是E（s，t）越大，分裂效果越好。

2.2 集成學習

集成學習是將多棵CART決策樹組合在一起，每棵決策樹對分類或回歸的結果進行投票，決定最后的預測結果。由于單一CART決策樹回歸的精度不高，容易出現過擬合、陷入局部最優等問題。為克服單一CART決策樹的缺點，Breiman在隨機森林中引入Bagging算法，該算法依據統計學中Bootstrap思想，從原始樣本中可放回重復抽樣獲取等規模的訓練樣本，并將生成的CART決策樹組合進行集成學習，提高了分類器的泛化能力［17］。假設N是原始數據集D的樣本容量，那么D中每個樣本沒有被抽到的概率為1／（1－1／N）N，且當 N趨于 ∞ 時，1／（1－1／N）N收斂于1／e≈0.368。該結果表明原始數據集D中大約有37%的樣本不被抽到，這些未被抽中的Bootstrap數據稱為袋外（OOB）數據。Breiman證明了利用隨機特征構建決策樹和OOB估計泛化誤差，有利于提高預測的精度［18］。此外Bagging算法可以同時進行多棵決策樹訓練，減少了計算的時間，也是該算法的優勢

2.3 隨機森林算法

隨機森林是｛H（X，θi），i＝1，2，...，k｝k個決策樹集成學習的組合分類器，針對回歸問題，取H（X，θk）的預測平均值作為最后的預測結果。

設 D＝｛（xi，yj）i＝1，2，...，N；j＝1，2，...，m｝為訓練數據集，其中x是數據集D的一個訓練樣本，y為樣本的特征變量，原始訓練數據集有N個記錄，M個特征變量，算法過程見圖1。

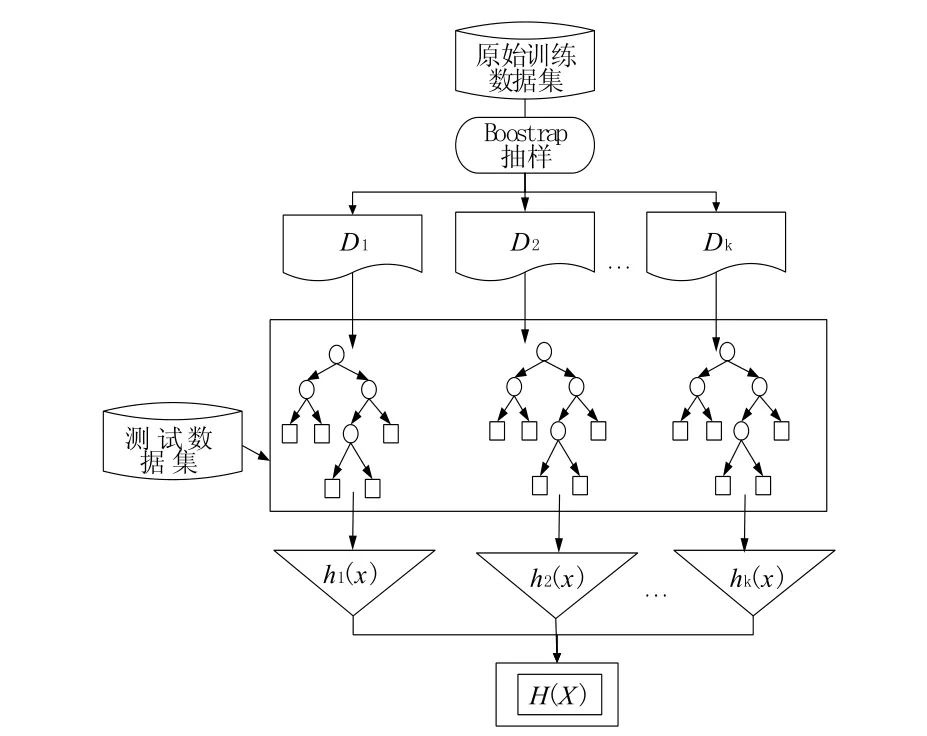
圖1 隨機森林算法的結構圖Fig.1 Structure diagram of random forest algorithm

該算法的基本流程為：

（1）從數據集D中，boostrap抽樣得到與原始數據集容量一樣的K個數據集，構建K個訓練子集。每個數據集包括N個樣本和m個特征變量，即從N個記錄boostrap抽樣抽取N個記錄，從原始數據集的M個特征變量中抽取得到m個特征變量，反復抽樣k次，形成訓練樣本集Dtrain。

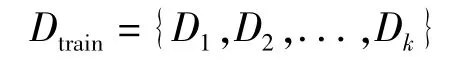
（2）根據CART決策樹算法，構建隨機森林里的決策樹。這些決策樹利用CART決策樹算法進行訓練，決策樹在生長過程中，隨機從M個特征變量中選擇m個特征變量，利用最小二偏差法計算出最優的特征變量作為分裂節點。進行決策樹訓練之后，利用袋外（OOB）數據作測試集 S＝｛S1，S2，...，Sk｝，有利于提高預測精度。

（3）假設每棵決策樹預測的輸出為 ｛Y1，Y2，...，Yk｝，隨機森林最后的預測結果為所有決策樹預測的平均值，即：

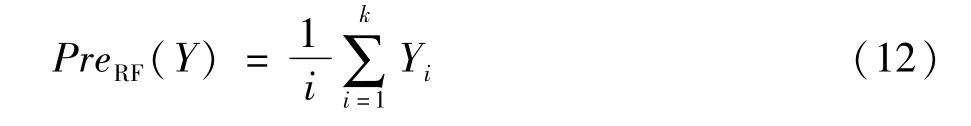
3 模糊聚類結合隨機森林的短期負荷預測理論分析

3.1 預測輸入變量

由于影響負荷預測的因素眾多，為了提高負荷預測的準確度，考慮將日氣象因素和實時氣象因素以及歷史負荷結合建立預測模型，本文選擇的輸入預測樣本參量，如表1所示。

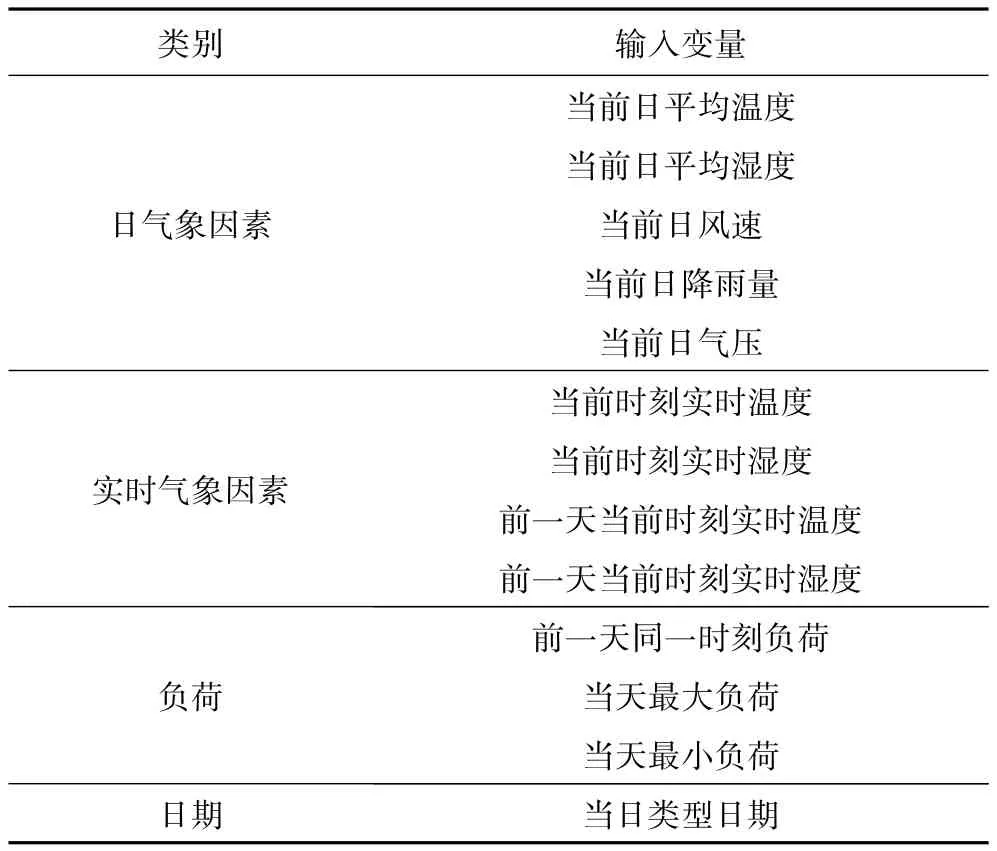
表1 輸入變量Tab.1 Input variables

3.2 數據的處理

由于輸入輸出數據單位不一致，在進行模型訓練前，應對輸入、輸出的氣象數據和負荷數據進行歸一化處理，取值范圍限定在［0，1］或［－1，1］之間，歸一化公式為：

式中xmax和xmin代表的是數據集的最大和最小值。

3.3 負荷預測流程

模糊聚類和隨機森林進行短期負荷預測時，利用模糊聚類算法將預測樣本分類后，找到待預測點所對應的類別，所屬類別對應的樣本作為隨機森林預測模型的輸入樣本，得到最終的預測結果，如圖2所示。

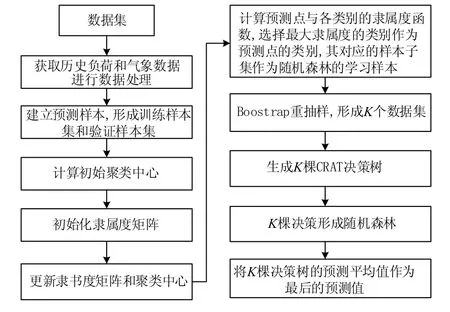
圖2 負荷預測流程圖Fig.2 Flow chart of load forecasting

4 應用實例及結果分析

本文結合安徽某地區歷史負荷數據和氣象數據對該地區2009年4月29日全天24小時的負荷進行預測，并將模糊聚類和隨機森林結合（IRF）的預測結果與傳統的SVM算法和BP神經網絡所得預測結果進行比較，如表2所示。表2的時間是從0∶01∶00-0∶24∶00。

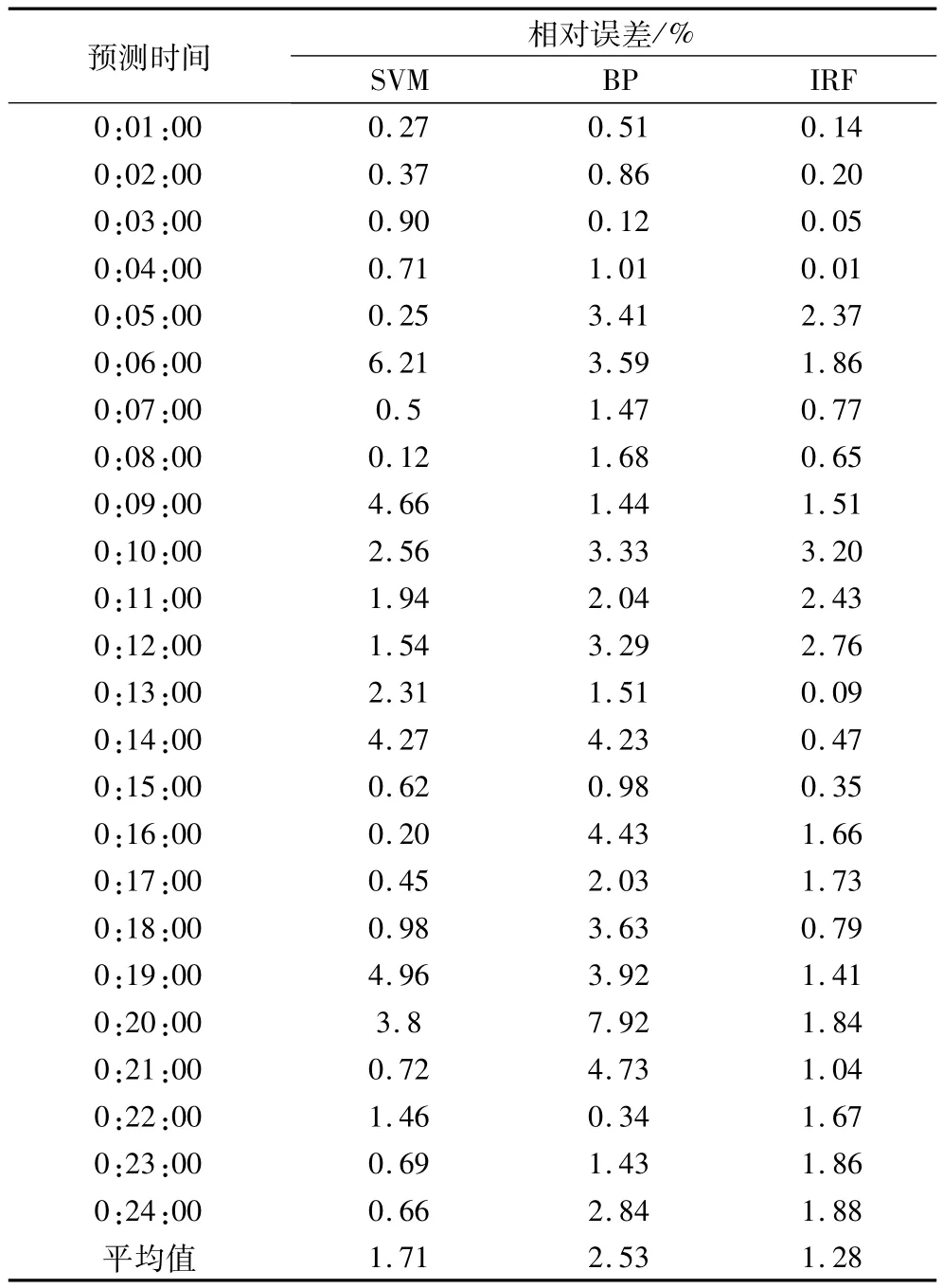
表2 三種方法的預測結果對比Tab.2 Comparison of the prediction results of the threemethods

畫出2009年4月29日3種方法預測的負荷曲線對比圖，見圖3。

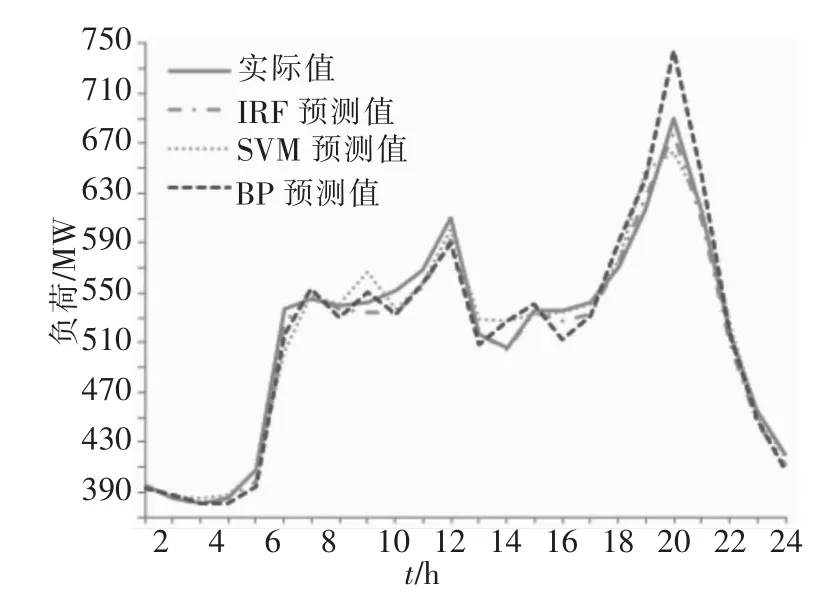
圖3 2009年4月29日3種方法預測的負荷曲線Fig.3 Comparison of threemethod of forecasting load curves on 29，April 2009

與其它兩種方法的結果比較，本文方法得出的負荷預測曲線更接近實際負荷曲線，為清楚觀察對比結果，分別計算24小時平均相對誤差和平均絕對百分比誤差（MAPE）得到表2，MAPE計算公式為：

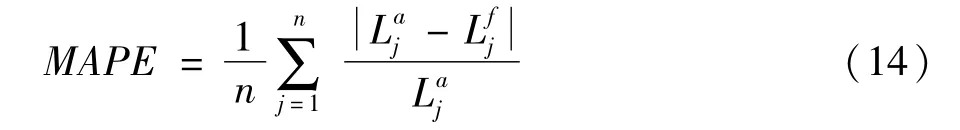
由表2得知，模糊聚類和隨機森林結合進行負荷預測結果優于傳統的SVM算法和BP神經網絡方法預測結果，為了進一步證明所提算法的有效性，本文對2009年4月28～5月4日連續工作日的24小時的負荷進行預測，其中5月1日～5月3日為節假日，結果見表3。

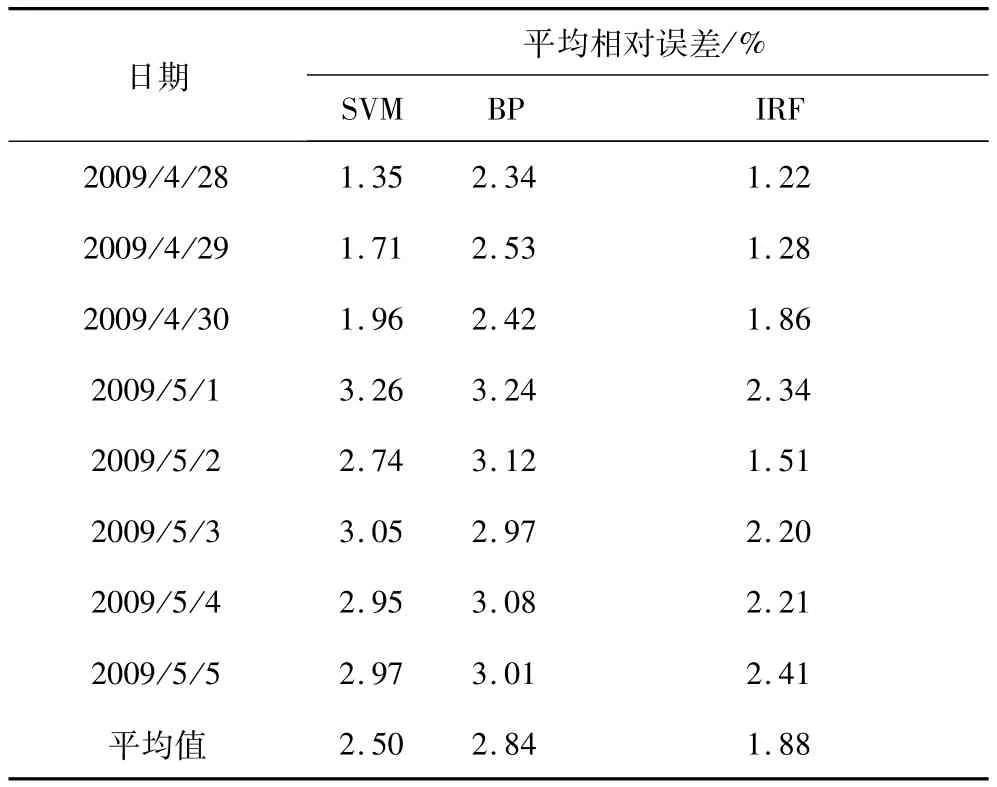
表3 4月28日～5月4日三種方法的預測精度對比Tab.3 Comparison of the prediction accuracy from April 28 to May 4 results about threemethods

由表3可知，本文所提出方法的負荷預預測精度高于傳統的SVM方法預測精度，且5月1日～5月3日為節假日的預測誤差明顯小于SVM的預測誤差，體現了該方法較好的魯棒性。

5 結束語

本文提出模糊聚類與隨機森林相結合的方法進行負荷預測，該方法利用隨機森林算法的泛化能力高、魯棒性好的優勢，同時結合模糊聚類算法選取相似度高的輸入樣本作為隨機森林預測模型的訓練樣本，不僅保證輸入特征量的一致性而且簡化了訓練模型。實例表明，與傳統的SVM和BP神經網絡方法相比，該方法并有效地提高了短期負荷預測的精度，為電力需求側負荷管理提供了一定的參考依據。