協(xié)變量缺失下加速失效時間模型基于經(jīng)驗似然的加權(quán)估計

袁曉惠，陳 晶

(長春工業(yè)大學(xué)基礎(chǔ)科學(xué)學(xué)院，吉林 長春 130012)

協(xié)變量缺失下加速失效時間模型基于經(jīng)驗似然的加權(quán)估計

袁曉惠，陳 晶

(長春工業(yè)大學(xué)基礎(chǔ)科學(xué)學(xué)院，吉林 長春 130012)

在部分協(xié)變量數(shù)據(jù)缺失的加速失效時間模型中，提出了參數(shù)的逆概率加權(quán)(IPW)估計和基于經(jīng)驗似然的加權(quán)(ELW)估計，證明了這兩種估計的大樣本性質(zhì).結(jié)果表明，ELW估計計算簡單，且對回歸參數(shù)的估計效率高于IPW估計.

加速失效時間模型；經(jīng)驗似然推斷；協(xié)變量缺失；秩；加權(quán)估計

加速失效時間模型(accelerated failure time model)[1]是生存分析領(lǐng)域比較經(jīng)典的模型之一.它假定失效時間(響應(yīng)變量)經(jīng)過某種單調(diào)變換(通常是對數(shù)變換)后與協(xié)變量具有線性關(guān)系，因其模型形式接近于一般的線性回歸方程，故回歸參數(shù)的解釋也與一般線性回歸相似.對于此模型回歸參數(shù)的半?yún)?shù)推斷，比較經(jīng)典的有Buckley-James估計[2]和秩估計[3-4].

在現(xiàn)實生活中缺失數(shù)據(jù)現(xiàn)象是無處不在的，例如醫(yī)學(xué)研究、民意調(diào)查、生物遺傳及市場調(diào)研等都會因人為或客觀因素出現(xiàn)缺失數(shù)據(jù).對于個體觀測有缺失的數(shù)據(jù)，最簡單的方法是直接剔除掉數(shù)據(jù)不完整的個體，然后對余下的完整數(shù)據(jù)進(jìn)行統(tǒng)計分析，即CCA方法.然而僅僅基于余下的完整數(shù)據(jù)進(jìn)行的統(tǒng)計分析可能效率較低，而且如果數(shù)據(jù)不是完全隨機(jī)缺失的話，統(tǒng)計推斷結(jié)果還有可能出現(xiàn)很大偏差，甚至導(dǎo)致錯誤的推斷，所以缺失問題得到了眾多學(xué)者的廣泛研究.[5-9]

在部分協(xié)變量隨機(jī)缺失的加速失效時間模型下，Nan等[10]由基于秩的加權(quán)估計方程得到參數(shù)的相合估計.Yu[11]基于調(diào)整的Buckley-James估計方程得到參數(shù)的相合估計.以上兩種估計都是基于非光滑的估計方程，可能會降低求解估計的計算效率.

經(jīng)驗似然是一種非參數(shù)統(tǒng)計方法，可以對所關(guān)心的參數(shù)做點估計和置信域估計.經(jīng)驗似然以其有效性和靈活性得到了廣泛關(guān)注與應(yīng)用.Owen[12]對經(jīng)驗似然的研究進(jìn)展進(jìn)行了比較詳盡的綜述.

本文考慮加速失效時間模型中部分協(xié)變量隨機(jī)缺失的情形.首先介紹了回歸參數(shù)的CCA估計，然后提出了IPW估計并給出了IPW估計的漸近分布，接著提出ELW估計并證明了ELW估計的大樣本性質(zhì).從漸近方差可以看出，ELW估計比IPW估計更高效.

1 加速失效時間模型及CCA估計

(1)

當(dāng)數(shù)據(jù)沒有缺失時，在模型(1)的假設(shè)下，Tsiatis[13]構(gòu)造了β*的秩估計函數(shù)

(2)

(3)

易知Un(β)是凸目標(biāo)函數(shù)Ln(β)的梯度，

可以通過最小化Ln(β)求出β*的估計.

(4)

2 逆概率加權(quán)估計

在數(shù)據(jù)隨機(jī)缺失機(jī)制下，Robins等[5]利用逆概率加權(quán)(IPW)[6]的想法得到了估計方程中所關(guān)心參數(shù)的無偏估計.IPW方法首先估計出數(shù)據(jù)缺失的概率πi，然后將δi/πi作為權(quán)函數(shù)加入估計方程中，使得估計方程無偏，得到參數(shù)β*的相合估計.

假設(shè)協(xié)變量數(shù)據(jù)是隨機(jī)缺失的，即在給定(yi，di，zi)時，δi和xi條件獨立：

P(δi=1|yi，xi，di，zi)=P(δ=1|yi，di，zi)=πi.

本文選用參數(shù)模型來估計πi.假定πi=πi(γ*),γ的對數(shù)似然函數(shù)為

(5)

引理1假定πi(γ)被正確指定、有界、三階可導(dǎo)，且存在c>0使得infπi(γ)>c>0.那么當(dāng)n→∞時，

引理1的證明可由中心極限定理和大數(shù)定律得到，此處略去.

(7)

定理1假定πi(γ)被正確指定.若引理1的條件和文獻(xiàn)[3]中條件1—4 都滿足，則當(dāng)n→∞時，

其中

這里ζ(·)是誤差e的風(fēng)險函數(shù)，ζ′(·)是其導(dǎo)數(shù).

證明令

(8)

其中

由文獻(xiàn)[3]可以得到

(9)

(10)

結(jié)合(9)和(10)式，

3 經(jīng)驗似然加權(quán)估計

令pi為(y，d，x，z，δ)的聯(lián)合分布在(yi，di，xi，zi，δi)的概率質(zhì)量，且滿足約束條件

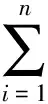
(11)

(12)

(13)

其中

為證明定理2，先給出下面引理.

‖λ(α，β，γ)‖=Op(n-1/2)，

且

對于θ∈B一致成立.其中B是包含真值且半徑小于cn-1/2的閉球，0

證明主要證明第一式，第二式的證明類似.由于

其中μ1=πi(γ*)，μ0=1-πi(γ*).對此式關(guān)于γ求偏導(dǎo)數(shù)得

經(jīng)過簡單的運(yùn)算有

因此

(14)

由文獻(xiàn)[3]之定理2，

(15)

結(jié)合(14)—(15)式可得

(16)

將(6)和(14)式代入(16)式，適當(dāng)化簡有

[1] KALBFLEISCH J D，PRENTICE R L.The statistical analysis of failure time data[M].Hoboken：John Wiley & Sons，2002：218-246.

[2] BUCKLEY J，JAMES I.Linear regression with censored data[J].Biometrika，1979：66(3)：429-436.

[3] YING Z.A large sample study of rank estimation for censored regression data[J].The Annals of Statistics，1993，21(1)：76-99.

[4] JIN Z，LIN D Y，WEI L J，et al.Rank-based inference for the accelerated failure time model[J].Biometrika，2003，90(2)：341-353.

[5] ROBINS J M，ROTNITZKY A，ZHAO L P.Estimation of regression coefficients when some regressors are not always observed[J].Journal of the American statistical Association，1994，89：846-866.

[6] HORVITZ D G，THOMPSON D J.A generalization of sampling without replacement from a finite universe[J].Journal of the American statistical Association，1952，47：663-685.

[7] WANG Q，LINTON O，HARDLE W.Semiparametric regression analysis with missing response at random[J].Journal of the American Statistical Association，2004，99：334-345.

[8] 劉銀萍.具有部分缺失數(shù)據(jù)兩個正態(tài)總體的估計和檢驗[J].東北師大學(xué)報(自然科學(xué)版)，2002，34(4)：15-19.

[9] TANG C Y，QIN Y.An efficient empirical likelihood approach for estimating equations with missing data[J].Biometrika，2012，99(4)：1001-1007.

[10] NAN B，KALBFLEISCH J D，YU M.Asymptotic theory for the semiparametric accelerated failure time model with missing data[J].The Annals of Statistics，2009，37(5)：2351-2376.

[11] YU M.Buckley-James type estimator for censored data with covariates missing by design[J].Scandinavian Journal of Statistics，2011，38(2)：252-267.

[12] OWEN A B.Empirical likelihood[M].Hoboken：John Wiley & Sons，2001：29-216.

[13] TSIATIS A A.Estimating regression parameters using linear rank tests for censored data[J].The Annals of Statistics，1990，18(1)：354-372.

[14] FYGENSON M，RITOV Y.Monotone estimating equations for censored data[J].The Annals of Statistics，1994，22(2)：732-746.

[15] LIU T，YUAN X.Weighted quantile regression with missing covariates using empirical likelihood[J].Statistics，2016，50(1)：89-113.

[16] QIN J，ZHANG B，LEUNG D H Y.Empirical likelihood in missing data problems[J].Journal of the American Statistical Association，2009，104：1492-1503.

[17] KITAMURA Y，TRIPATHI G，AHN H.Empirical likelihood-based inference in conditional moment restriction models[J].Econometrica，2004，72(6)：1667-1714.

Weightedestimatorfortheacceleratedfailuretimemodelwithmissingcovariatesbasedonempiricallikelihood

YUAN Xiao-hui，CHEN Jing

(School of Basic Sciences，Changchun University of Technology，Changchun 130012，China)

The inverse probability weighted (IPW) estimator and the empirical likelihood-based weighted estimator (ELW) for the accelerated failure time model with missing covariates are proposed，and the large sample properties of the proposed methods are given.It shows that the ELW estimator is computationally simple and more efficient than the IPW estimator.

accelerated failure time model；empirical likelihood；missing covariates；rank；weighted estimator

1000-1832(2017)04-0032-06

10.16163/j.cnki.22-1123/n.2017.04.007

2016-03-01

國家自然科學(xué)基金資助項目(11401048，11671054)；吉林省青年科研基金資助項目(20150520055JH).

袁曉惠(1983—)，女，博士，講師，主要從事不完全數(shù)據(jù)研究；陳晶(1991—)，女，碩士，主要從事刪失數(shù)據(jù)研究.

O212.1學(xué)科代碼110·67

A

(責(zé)任編輯：李亞軍)