求解TSP問題的離散型差分進化算法?

寧桂英 曹敦虔 周永權

（1.廣西科技大學鹿山學院 柳州 545616）（2.廣西民族大學理學院 南寧 530006）（3.廣西民族大學信息科學與工程學院 南寧 530006）

求解TSP問題的離散型差分進化算法?

寧桂英1曹敦虔2周永權3

（1.廣西科技大學鹿山學院 柳州 545616）（2.廣西民族大學理學院 南寧 530006）（3.廣西民族大學信息科學與工程學院 南寧 530006）

針對旅行商（TSP）問題，提出了一種離散型差分進化算法，在該算法中，一方面，采用一種新的編碼方法，把僅用于求解連續域上優化問題的差分進化算法推廣到能用于求解離散TSP問題；另一方面，引入了2-OPT算子，將全局搜索與局部搜索有機地結合，通過對經典的TSP問題實例進行了測試，仿真結果表明，論文提出的算法具有較強的穩定性，是求解TSP問題的一種有效的方法。

差分進化；旅行商；啟發式算法；適應度；2-OPT

1 引言

旅行商問題（traveling salesman problem，簡稱TSP）已被證明是一個典型的難以求解的NP-hand問題，它在生產線布局領域、庫存配送領域及工程優化等領域有著廣泛的應用，因此，尋找TSP問題的解具有重要的理論意義與實際應用價值。對TSP求解問題，目前的方法主要分為兩大類：一類是精確算法（exact algorithms），如動態規劃法、分支界限法、Dijkstra算法、Floyd算法、Bellman-Ford算法及改進的SPFA算法等［1］。這些算法的思想比較容易理解，理論上也能得到最優解，但在計算效率上不盡人意，難以解決大規模的問題；另一類是啟發式算法（heuristic algorithms），如遺傳算法（Genetic Algorithm，A）、模擬退火算法（Simulated Annealing，SA）、蟻群優化算法（Ant Colony Optimization，ACO）、禁忌搜索算法（Tabu Search，TS），最近領域搜索（Nearest Neighbor，NN）［2］、分層協同進化免疫算法（Hierarchical Co-evolution Immune Algorithm，HCIA）［3］、細菌覓食算法（Bacterial Foraging Algorithm）［4］及混合蛙跳算法（Shuffled Frog-Leaping Algorithm，SFLA）［5］等。這些算法雖不能保證在有限的時間內一定能得到問題的最優解，但通過大量的試驗表明，這些啟發式算法最終得到的最優解的誤差能達到令人滿意的程度。因此，啟發式的群優化方法已成為目前人們求解TSP問題的一種有效方法。

差分進化算法（Differential Evolution，簡稱DE）是一種基于實數編碼的，用于求解連續域上優化問題的智能優化算法，它是1995年由Storn和Price提出的，此后憑借其穩健性和強大的全局尋優能力在眾多應用領域取得成功［6～7］，如：圖像處理、最優設計、參數識別等，盡管DE算法憑借其強有力的性能在連續優化問題上取得了巨大成功，但是在離散優化問題上應用較少，鑒于此，本文提出用離散差分進化算法（DDEA）求解TSP問題，該算法一方面結合TSP問題本身的特點，對DE算法提出了一種特殊的適用于求解離散問題的編碼方法，另一方面，為了增強算法的局部搜索能力，加快收斂速度，在DE算法中引入具有較強局部搜索能力的2OPT算子［8］，最后為了驗證本文提出算法的性能，對14到200個經典的TSP問題進行了仿真，實驗結果表明，本文提出的算法在解決中小規模的TSP問題中能夠以較快的速度得到問題的最優解，驗證了本文算法的有效性。

2 TSP問題概述

設某旅行商要拜訪n個城市，規定每個城市必需且只能拜訪一次，最后回到原出發城市，要求選擇一條路徑，使其沿著該路徑行走的路程為所有路徑中的最小值。

TSP模型可以表示為：設n個城市之間的距離矩陣為 D=(dij)n×n，其中dij代表城市i到城市 j的距離（i≠j），若i=j，定義 dij為一個足夠大的實數M ，設 n（n＞3）個城市分別標號為（1，2，…，n），一個TSP問題的可行解就是n個城市標號的環狀排列，令π(n)為存放n個城市的任意排列的一維數組，則可行解的旅行總距離可表示為

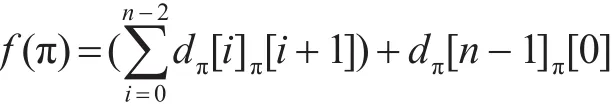
一個TSP問題的最優解是使 f(π)取得最小值的排列［9］。

3 求解TSP問題的離散型差分進化算法

3.1 標準DE算法步驟

3.1.1 變異操作

變異是差分進化算法用來產生新個體的一個關鍵步驟，變異操作主要通過下式進行：

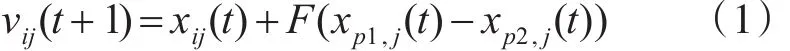
其中：xp1，xp2為任意選擇的兩個個體，p1，p2為［1，M］中任意選取的互不相等的隨機整數，F為變異因子，i=1，2，…，M.j=1，2，…，n。

3.1.2 交叉操作

DE算法的交叉操作是將變異后的新個體與當前個體混合，然后按照以下規則選擇哪個個體將進入下一代，交叉操作通常按下式進行：

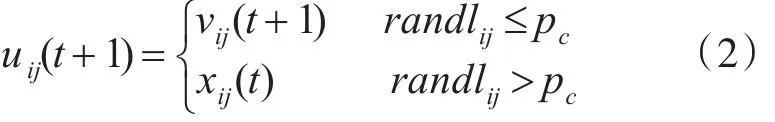
其中 pc為交叉因子，通常 pc取（0，1］之間的實數，randlij為［0，1］間隨機數。

3.1.3 選擇操作

為保證新生成的個體Ui是否進入下一代中，DE算法在進行交叉操作后，需要將新生成個體的適應度與當前種群中個體Xi的適應度進行比較。如果Ui的適應度優于 Xi，則選擇Ui進入下一代；否則，直接讓舊個體Xi進入下一代，具體操作為

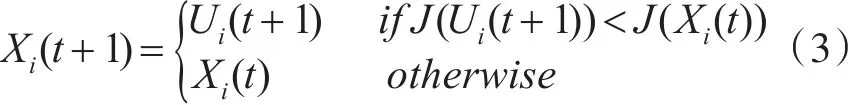
3.2 編碼設計

變異操作是DE算法的主要操作，但這種操作是基于實數域上的四則運算，因此適用于連續域上的優化問題，而對于離散域上的組合優化問題的解是自然數的情況已不能滿足要求。為了既保留DE算法變異算子的功能，又能解決離散域上的優化問題，本文提出一種特殊的編碼方式。對包含n個城市的一個TSP問題，一個可行的編碼是1到n上的隨機整數構成的一個序列，如：序列（3，2，4，1，5）表示編號為3的城市在1號位置，編號為2的城市在2號位置，編號為4的城市在3號位置，編號為1的城市在4號位置，編號為5的城市在5號位置。通過DE變異算子之后，整數的運算不再滿足封閉性，但是實數是有大小之分的，因此，可通過對變異后的實數按由小到大排序后再找出原來的數在新序中的位置這一方法來解決離散域上的優化問題。下面給出這一編碼的定義。

定義1：設 Xi(t)=(xi1(t)，xi2(t)，…，xin(t))為DE算法第t代的一個基本個體，X'i(t)=(xi1'(t)，xi2'(t)，…，(t))為 Xi(t)按由小到大排序后的新個體，若xij(t)?x'im(t)，則稱個體分量xij(t)經變異后對應分量為m。

如基本個體（-2.3，4.1，3.2，-1.5，2.4），升序排列后的個體為（-2.3，-1.5，2.4，3.2，4.1），對應的編碼為（1，5，4，2，3）。

據定義1，通過DE算法的變異算子之后的任何個體均有一組對應的整數編碼與之對應，因此，通過這種編碼方法可以解決離散域上的TSP問題。

3.3 局部路徑優化設計

盡管已有大量實驗證明DE算法具有較強的穩定性和全局搜索能力，但與其它優化算法一樣，標準DE算法也會存在收斂速度慢，易陷入局部極優等不足。因此，在求解TSP這一NP-hard問題時，考慮引入具有全局搜索能力的優化策略。已有文獻表明，求解TSP問題的算法分為兩大類型：一種是局部啟發式搜索算法；一種是獨立于問題的經典優化算法。常見的局部啟發式優化算法有2-OPT，3-OPT和Lin-Kernighan（LK）等［8，10］。實驗證明，在這些算法中，用2-OPT算子優化路徑對求解TSP問題的局部最優解非常有效。但僅靠2-OPT算子本身的特性也會使問題陷于局部最優，因此，本文考慮首次將將具有較強全局搜索能力的DE智能算法與具有局部優化能力的2-OPT算子相結合，在進化前期用具有較強搜索能力的DE算法進行全面搜索，以增強群體的多樣性，到后期對得到的路徑再用2-OPT算子進行局部優化，以提高收斂速度和精度。

3.4 Complete 2-Opt（C2Opt）算子

在本文的算法中，先用DE算法對群體進行優化后，再對所有構成路徑用C2OPT算子進行局部優化。

設ck為城市所在頂點，d(ci，cj)表示任意兩個城市i與 j之間的距離，C2OPT算子的具體步驟如下［8］：

Step 1：選 取 一 條 路 徑 c={c1，…，ci，ci+1，…，cj，cj+1，…，cn-1}，并令 i=j=0 ；

Step 2：任選一條邊，記為No.1：(ci，ci+1)，其中i＜n；

Step 3：任選另一條邊，記為No.2：(cj，cj+1)，其中i＜n；

Step 4：如 果 |j-(i+1)| ≥2 且 d(ci，cj)+d(ci+1，cj+1)＜ d(ci，ci+1)+d(cj，cj+1)，則用 2-Opt算子刪 除 邊 (ci，ci+1) 與 (cj，cj+1) ，并 連 接 邊 (ci，cj) 和(ci+1，cj+1)且 ci+1與 cj的指向相反；

Step 5：再以cj作為No.2邊下一個開始的城市，并令 j=j+1，重復Step 3～Step 4，直到 j=n-1，如果 j=n-1，令 j+1=0；

Step 6：以ci作為No.1邊下一個開始的城市，并 i=i+1令，重復Step 2～ Step 5，直到 i=n-1，如果i=n-1，令i+1=0；

Step 7：重復Step 2～Step 6直到 N 次，使 N 足夠大，直到所選取的路徑無交叉邊出現時終止。

圖1和圖2給出了使用C2OPT算子前和使用C2OPT算子后的示意圖。

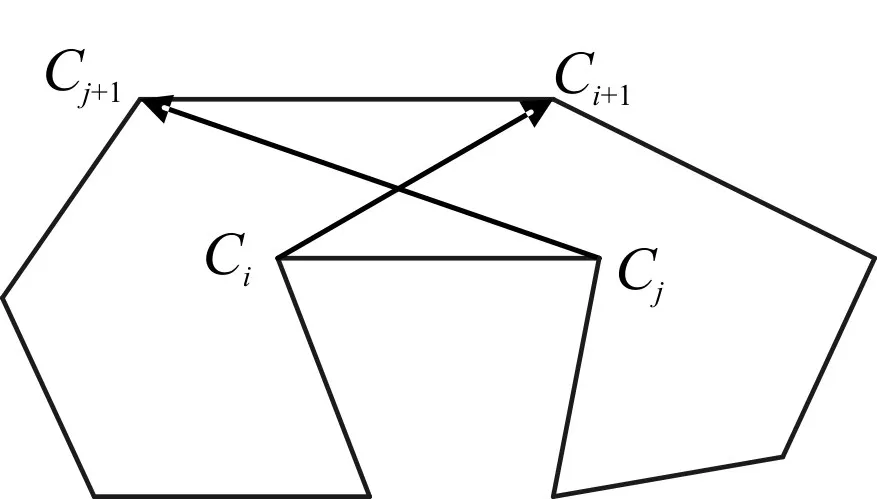
圖1 使用C2OPT算子前

圖2 使用C2OPT算子后

3.5 適應度函數選取

本文適應度函數取優化后對應路徑長度的最小值。

3.6 參數設計

變異和交叉操作是DE算法的主要操作，而變異因子和交叉因子選取的好壞直接影響算法的性能，到目前為止，還沒有一種選取方式能適合解決所有問題，據現有文獻給出的范圍，本文給出了變異算子F和交叉算子CR的最佳取值。以14個城市的TSP問題為例，此問題的已知的最優路徑和為30.8785。

表1 不同參數運行結果

表1中給出了參數不同取值后運行10次所得平均結果。從表中可看出，求解TSP問題時，變異算子F和交叉算子CR的取值的不同對結果的影響很大，當F=0.5，CR=0.2時優化效果最好，從運行10次的平均值來看，此時的結果與最優值相當。因此，在本文算法中設置F=0.5，CR=0.2。

3.7 求解TSP問題的離散型DE算法具體步驟：

Step 1.初始化。隨機生成1～n上的一個自然數序列，構成一個個體，依次生成m個初始種群，設置最大進化代數T，變異算子F和交叉算子CR；

Step 2.計算各個體的適應度；

Step 3.利用式（1）進行變異操作；

Step 4.對變異后的算子利用式定義1方法編碼；

Step 5.利用式（2）進行交叉操作；

Step 6.對交叉后的個體利用2opt算子進行局部優化，生成新個體；

Step 7.選擇操作；

Step 8.判斷是否達到迭代要求，若是，停止，并輸出路徑和的最優結果，若否，則轉Step 3。

4 算法性能分析

對本文提出的算法，在線性能定義如下：

定義2：設 f(t)為第t代群體的平均適應度，T為進化代數，則在同樣的環境下，稱為算法的在線性能。

在線性能表示算法在直到當前為止的時間內得到的所有性能的平均值，反映了算法的動態性能，圖3給出了本文算法的在線性能曲線。

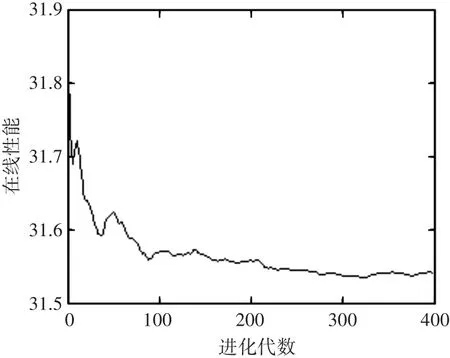
圖3 在線性能曲線圖

從圖3可以看出，本文提出的算法具有較強的穩定性。

5 算例測試

由于Oliver30和Eil51經常被用來測試各種算法的測試實例，因此本文首先測試了Burma14，坐標為（16.47，96.10），（16.47，94.44），（20.09，92.54），（22.39，93.37），（25.23，97.24），（22，96.05），（20.47，97.02），（17.20，96.29），（16.30，97.38），（14.05，98.12），（16.53，97.38），（21.52，95.59），（19.41，97.13），（20.09，94.55）及Oliver30和Eil51的TSP問題，表2給出了本文算法的測試結果，并與文獻［12］DGSO算法和文獻［13］的SADPSO算法及文獻［14］的ACO算法的結果進行了比較，從測試結果可以看出，四種算法對Burma14都能找到最優解，而對于Oliver30問題，本文算法進化200代就找到最優解，而且進化代數遠比SADPSO少，收斂速度快，對Eil51問題，雖然與目前已知最優解有些差值，差值為1.3，但與文獻相比都有所改進，說明本文算法的有效性。

表2 本文算法與相關文獻結果比較

圖4～圖7分別給出了Oliver30和Eil51問題的最優路徑圖和進化曲線圖。

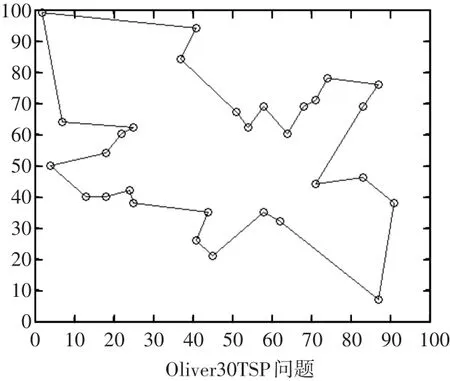
圖4 本文算法優化Oliver30算例的路徑圖

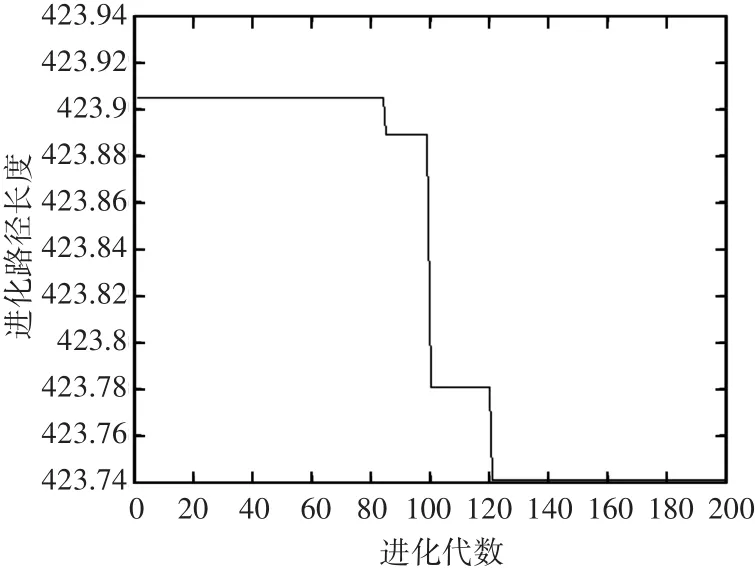
圖5 本文算法優化Oliver30算例的進化曲線圖

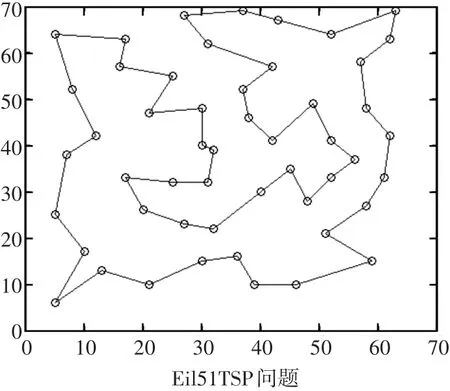
圖6 本文算法優化Eil51算例的路徑圖

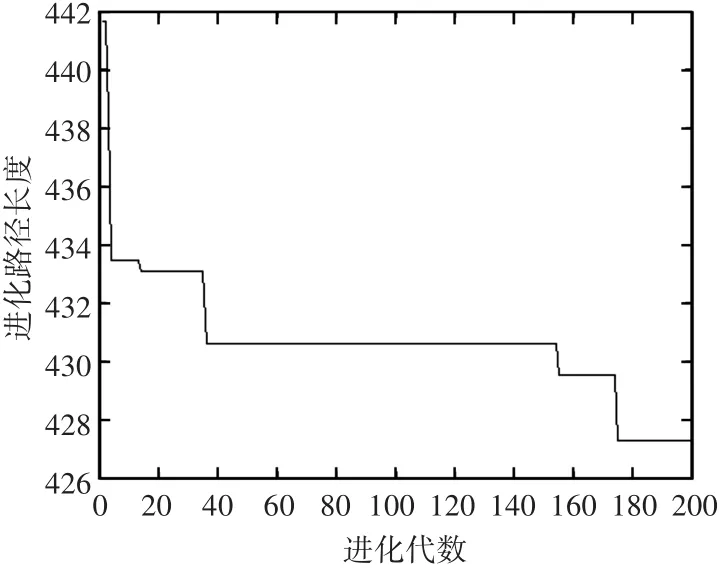
圖7 本文算法優化Eil51算例的進化曲線圖

為進一步驗證該算法的有效性，本文選自城市數量為 48～200 的 Att48、kroa100、bier127、pr144、kroa200幾個經典TSP問題進行了測試，這些測試實例選自國際通用的TSP標準庫TSPLIB［15］。TSPLIB是一個開放的網絡資源，其中收集了各種規模的TSP實例，并提供了所有實例的最優解作參考。為降低誤差，本文與所給文獻的參數設置基本保持一致，本文對每個算例運行10次，取其最優解，最差解和平均解作比較，并給出了本文算法所得結果的偏差率。最大進化代數為200，變異因子F=0.5，交叉因子CR=0.2，所得結果如表3所示。

從表3可以看出，對att48問題，本文算法每次都能找到問題的最優解，偏差為0，對Kroa100問題，雖然比標準庫多出1，但是比文獻［16］的改進的演化算法和文獻［18］的離散型細菌覓食算法及文獻［22］的多角色蟻群算法求解的結果好，而且進化代數少，耗時短，對bier127和kroa200問題，本文進化200代得到的最優結果較文獻［20］的ACO&&SS算法進化2000代的效果好，而且也明顯優于文獻［21～22］，充分顯示本文算法的優越性，對pr144問題，找到的最優解比標準庫給出的少2，從整個計算結果來看，本文算法計算偏差率都很低，說明該算法具有很強的穩定性和魯棒性，能有效解決中小規模的TSP問題。

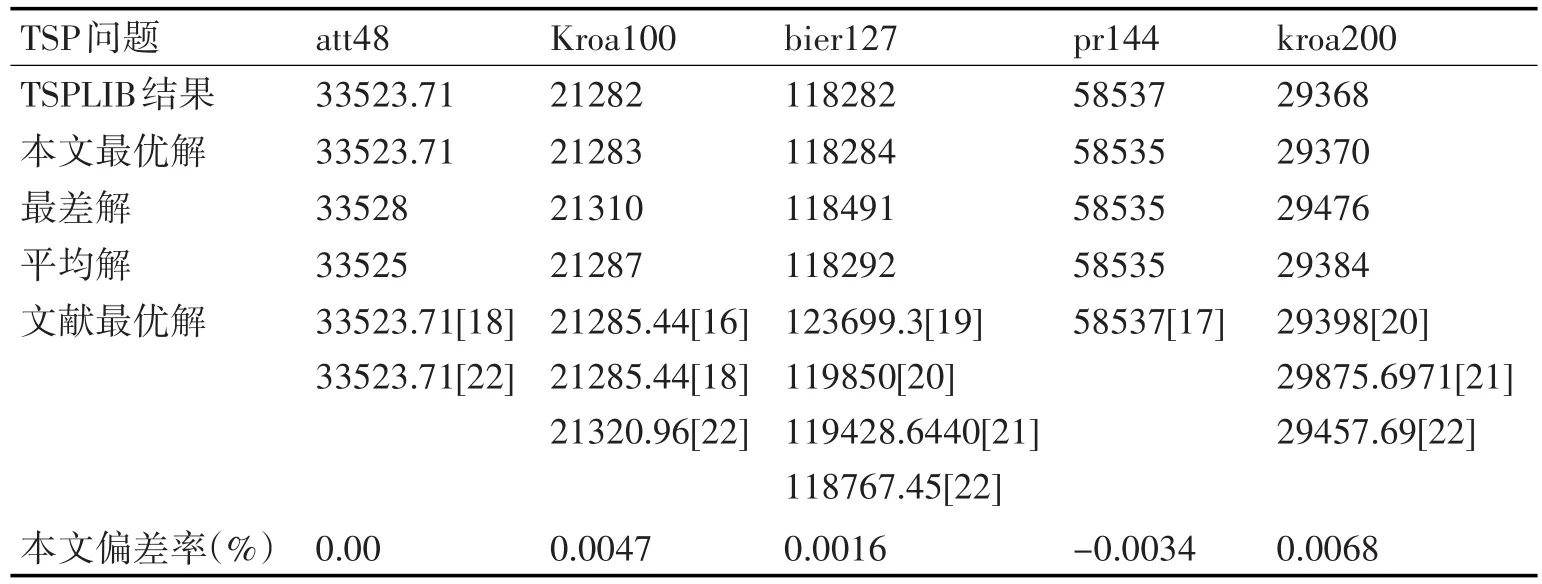
表3 本文算法計算結果與文獻結果對比

偏差率是體現計算結果與最優解的偏離程度，偏差率越小，表明算法越穩定。本文中提到的偏差率計算公式為

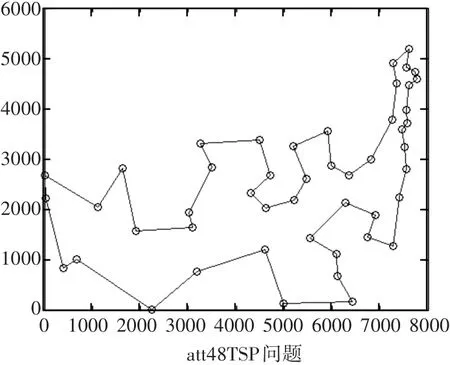
圖8 本文算法優化Att48算例的路徑圖

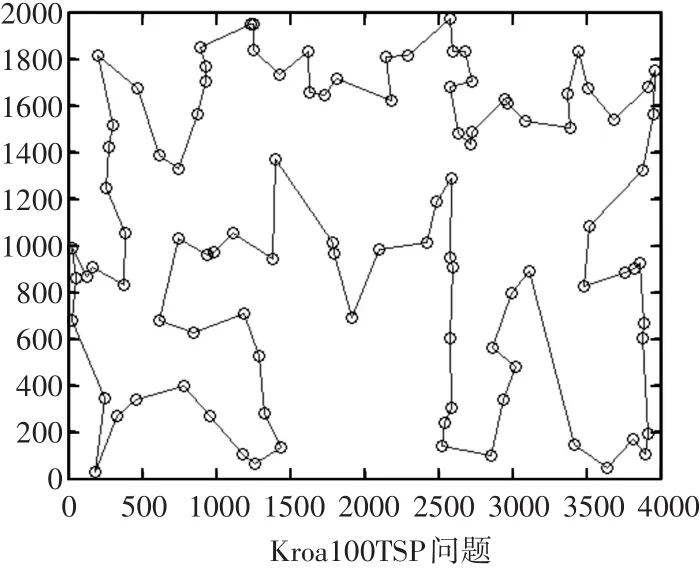
圖9 本文算法優化Kroa100算例的路徑圖

圖8～圖12給出了本文算例Att48、kroa100、bier127、pr144、kroa200的最優路徑圖

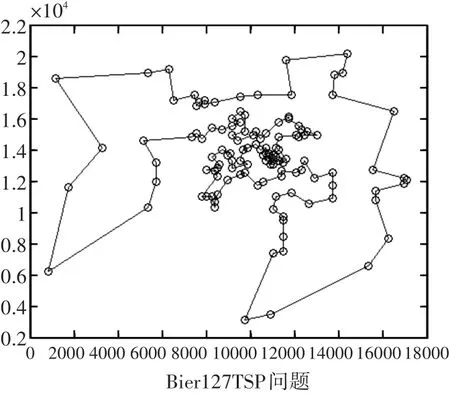
圖10 本文算法優化Bier127算例的路徑圖

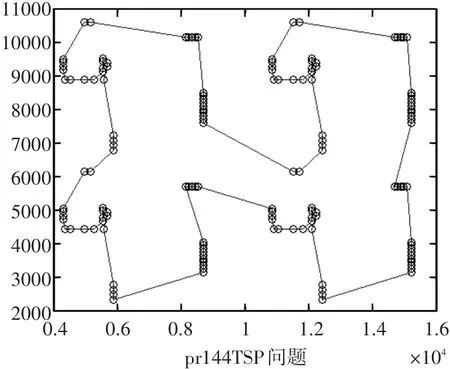
圖11 本文算法優化pr144算例的路徑圖

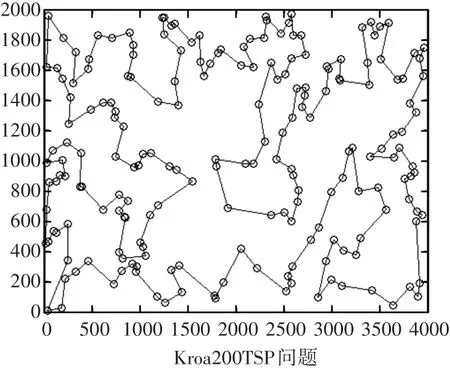
圖12 本文算法優化Kroa200算例的路徑圖

6 結語

本文針對求解TSP問題，提出了一種求解TSP問題的離散型差分進化算法，通過特殊的編碼方式和適當的參數測試設置，并首次將具有良好局部搜索能力的2-OPT算法與差分進化算法相融合，將僅用于求解連續域上優化問題算法拓展到用于解決離散組合優化問題。并選取了TSPLIB標準庫中的幾個14～200的TSP問題進行了測試仿真，仿真結果表明，在較少的進化代數的條件下，本文提出的算法所得到的最優解與TSPLIB中的最優解的偏差率都很低，說明本文算法在求解中小規模TSP問題時是有效可靠的。

今后的工作需將本算法進一步改進、優化以解決大規模的TSP問題及其它離散域上的復雜組合優化問題。

［1］李峰，莊東.運籌學［M］.機械工業出版社，2014（4）：243-255.LI Feng，ZHUANG Dong.Qperations Research［M］.China Machine Press，2014，4：243-255.

［2］武妍，包建軍.一種新的求解TSP的混合量子進化算法［J］.計算機應用，2006，26（10）：2433-2436.WU Yan，BAO Jianjun.New mixed quantum-inspired evolutionary algorithm for TSP［J］.Computer Applications，2006，26（10）：2433-2436.

［3］吳建輝，張兢，張小剛，等.分層協同進化免疫算法及其在 TSP 問題中的應用［J］.電子學報，2011，39（2）：336-340.WU Jianhui，ZHANG Jing，ZHANG Xiaogang，et al.Hierarchical Co-Evolution Immune Algorithm and Its Application on TSP［J］.Acta Electronica Sinica，2011，39（2）：336-340.

［4］尤夢麗，雷秀娟.改進的細菌覓食算法求解TSP問題［J］.廣 西 大 學 學 報 自 然 科 學 版 ，2013，38（6）：1437-1439.YOU Mengli，LEI Xiujuan.An improved bacterial foraging algorithm for the traveling salesman problem［J］.Journal of Guangxi University（Natural Science Edition），2013，38（6）：1437-1439.

［5］張敬敏，馬麗，李媛媛.求解TSP問題的改進混合蛙跳算法［J］.計算機工程與應用，2012，48（11）：47-50.ZHANG Jingmin，MA Li，LI Yuanyuan.Improved shuffled frog-leaping algorithm for traveling salesman problem［J］.Computer Engineering and Applications，2012，48（11）：47-50.

［6］曾宇容，王林，富慶亮.基于DE和PSO的混合智能算法及其在模糊EOQ模型中的應用［J］.計算機應用研究，2012，29（2）：438-441.ZENG Yurong，WANG Lin，FU Qingliang.Hybrid intelligent algorithm based on differential evolution and particle swarm optimization algorithm and its application in fuzzy EOQ model［J］.Application Research of Computers，2012，29（2）：438-441.

［7］WANG Lin，HE Jing，WU De-sheng，et al.A novel differential evolution algorithm for joint replenishment problem under interdependence and its application［J］.International Journal of Production Economics，2012，135（1）：190-198.

［8］Lin S.Kernigham B W.An effective heuristic algorithm for the travelling salesman problem［J］.Operations Research，1973，21（2）：4982-5161.

［9］Dorigo M.Stutzle T.Ant Colony Optimization［M］.Massachusetts：MIT Press，London，England，2004：69-75.

［10］祝崇雋，劉民，吳澄，等.針對模糊需求的VRP的兩種2-OPT算法［J］.電子學報，2001，29（8）：1035-1037.ZHU Chongjun，LIU Min，WU Cheng，et al.Two kinds of 2-opt algorithm for VRP with Fuzzy demand［J］.Acta Electronica Sinica，2001，29（8）：1035-1037.

［11］Peng Gang，Ichiro Ilmura，Shigeru Nakayma.An Evolutionary Multiple Heuristic with Genetic Local Search for Solving TSP［J］.International Journal of Information Technology，2008，14（2）：1-11.

［12］周永權，黃正新，劉洪霞.求解TSP問題的離散型螢火蟲群優化算法［J］.電子學報，2012，40（6）：1164-1170.ZHOU Yongquan，HUANG Zhengxin，LIU Hongxia.Discrete Glowworm Swarm Optimization Algorithm for TSP Problem［J］.Acta Electronica Sinica，2012，40（6）：1164-1170.

［13］張長勝，孫吉貴，歐陽丹彤.一種自適應離散粒子群算法 及 其 應 用 研 究［J］.電 子 學 報 ，2009，37（2）：299-304.ZHANG Changsheng，SUN Jigui，OUYANG Dantong.A Self-Adaptive Discrete Particle Swarm Optimization Algorithm［J］.Acta Electronica Sinica，2009，37（2）：299-304.

［14］吳慶洪，張紀會，徐心和.具有變異特征的蟻群算法［J］.計算機研究與發展，1999，36（10）：1240-1245.WU Qinghong，ZHANG Jihui，XU Xinhe.An ant colony algorithm with mutation features［J］.Journal of Computer Research and Development，1999，36（10）：1240-1245.

［15］ TSP Library.http：//www.Iwr.uni-heideberg.de/iwr.compot/software/TSPLIB95/TSP.LIB.html.

［16］蔡之華，彭錦國，高偉，等.一種改進的求解TSP問題的演化算法［J］.計算機學報，2005，28（5）：823-829.CAI Zhihua，PENG jinguo，GAO Wei，et al.An Improved Evolutionary Algorithm for the Traveling Salesman Problem［J］.Chinese Journal of Computers，2005，28（5）：823-829.

［17］孫光福，李程俊，張冬梅，等.一種求解TSP問題的演化算法［J］.計算機工程，2011，37（11）：209-211.SUN Guangfu，LI Chengjun，ZHANG Dongmei，et al.Evolutionary Algorithm for Solving Traveling Salesman Problem［J］.Computer Engineering，2011，37（11）：209-211.

［18］王勇臻，陳燕，李桃迎.離散型細菌覓食算法求解TSP問題［J］.計算機應用研究（網絡版），2014，31（12）：3642-3645.WANG Yongzhen，CHEN Yan，LI Taoying.Discrete bacteria foraging optimization algorithm for solving TSP［J］.Application Research of Computers，2014，31（12）：3642-3645.

［19］饒衛振，金淳，黃英藝.求解TSP問題的最近領域與插入混合算法［J］.系統工程理論與實踐，2011，31（8）：1420-1426.RAO Weizhen，JIN Chun，HUANG Yingyi.Hybird algorithm，of the nearest neighbor and insertion for the traveling salesman problem［J］.Systems Engineering-Theory&Practice，2011，31（8）：1420-1426.

［20］張曉霞，唐立新.一種求解TSP問題的ACO&&SS算法設計［J］.控制與決策，2008，23（7）：765-766.ZHANG Xiaoxia，TANG Lixin.An ACO＆SS algorithm for traveling salesman problem［J］.Control and Decision，2008，23（7）：762-766.

［21］王忠英，白艷萍，邱利霞.經過改進的求解TSP問題的蟻群算法［J］.數學的實踐與認識，2012，42（4）：133-140.WANG Zhongying，BAI Yan-ping，YUE Lixia.An Improved Ant Colony Algorithm for Solving TSP Problems［J］.Mathematics in Practice and Theory，2012，42（4）：133-140.

［22］杜鵬楨，唐振民，孫研.一種面向對象的多角色蟻群算法及其TSP問題求解［J］.控制與決策，2014，10（29）：1733-1734.DU Pengzhen，TANG Zhenmin，SUN Yan.An object-oriented multi-role ant colony optimization algorithm for solving TSP problem［J］.Control and Decision，2014，10（29）：1733-1734.

A Discrete Differential Evolution Algorithm for TSP Problem

NING Guiying1CAO Dunqian2ZHOU Yongquan3
（1.Lushan College of Guangxi University Science and Technology，Liuzhou 545616）（2.College of Science，Guangxi University for Nationalities，Nanning 530006）（3.College of Information Science and Engineering，Guangxi University for Nationalities，Nanning 530006）

A discrete differential evolution algorithm is proposed for solving traveling salesman problem（TSP）in this article.In the algorithm，on the one hand，the differential evolution algorithm with a new coding method is used to solve a discrete TSP，which is often used to solve problems on a continuous domain.On the other hand，the 2-OPT algorithm is also introduced；the new algorithm combined the global search with the local search effectively.The classical TSP has been tested，the simulation results show that the proposed algorithm has strong stability and it is an effective method for solving TSP.

differential evolution，TSP，heuristic algorithm，fitness，2-OPT

TP183

10.3969/j.issn.1672-9722.2017.11.012

Class Number TP183

2017年5月9日，

2017年6月29日

國家自然科學基金項目（編號：61463007）；2015年度廣西高校科學技術研究項目（編號：KY2015YB521）；2015年度廣西教育廳科學研究項目（編號：KY2015YB081）資助。

寧桂英，女，碩士，講師，研究方向：進化計算及應用。曹敦虔，男，碩士，講師，研究方向：計算智能及多元樣條函數。周永權，男，博士，教授，博導，研究方向：計算智能、智能優化、神經網絡。