基于特征相關性選擇的二硫鍵預測算法?

劉 坤

（南京理工大學計算機科學與工程學院 南京 210094）

基于特征相關性選擇的二硫鍵預測算法?

劉 坤

（南京理工大學計算機科學與工程學院 南京 210094）

二硫鍵是維持蛋白質結構與功能穩定的重要生物特征，先前關于二硫鍵模式的預測通常為將相關特征進行特征選擇并代入機器學習模型，其缺陷在于沒有考慮不同特征之間的關聯性，該文根據傳統的預測方法，在使用費舍得分進行特征選擇的基礎上，計算特征子空間中各特征的相關度，剔除線性相關度高的特征，利用支持向量回歸對處理后的數據進行四重交叉驗證，以取得更加理想的效果。

生物信息學；二硫鍵；支持向量回歸；相關系數；特征選擇

1 引言

蛋白質（protein）作為生命現象的物質基礎之一，是生命活動過程中的重要的物質承擔者，在生物體的生命過程中具有重要的作用。相比基因組學，蛋白質組學對于生命現象解釋更加直接、更加準確，近些年得到了快速發展，并得到了國內外學者廣泛重視。隨著20世紀90年代“人類基因組計劃”（Human Genome Project，HGP）工作的展開，以及后續公布的人類基因組圖譜和基本完成測序工作，已知蛋白質序列的數量呈爆炸性增長，標志著人類已經跨入到后基因組時代。

作為蛋白質重要的結構特征，二硫鍵是由兩個在相同或不同的蛋白質鏈上的半胱氨酸上形成的共價交聯，與蛋白質的折疊息息相關，可以維持蛋白質結構穩定［1］。目前為止，對二硫鍵的預測總體分為三類［2］：1）對二硫鍵的成鍵狀態預測；2）基于先驗知識對二硫鍵關聯模式的預測；3）對二硫鍵成鍵狀態與關聯模式共同預測。本文主要的研究方向為預測二硫鍵的關聯模式。

截至目前，二硫鍵預測工作已取得很大進展，預測算法有DISULFIND，Pair-wise SVM，GASVM，SS_SVR與FS_SVR等［3］。近期，對二硫鍵的預測主要基于機器學習的方法，首先提取原始特征，包括PSSM，PSS，DOC，CM，PTBCR等，然后對特征篩選，從大量特征中提取顯著特征，并利用合適的分類器（主要有支持向量回歸［4］與隨機森林［5］）進行預測與分類，得出重要的信息。

本文主要基于先驗知識，對二硫鍵關聯模式進行預測，預測同一條蛋白質鏈上形成的二硫鍵，從蛋白質序列出發，進行特征選擇后，對保留的特征子空間進行相關度計算，保留兩兩相關度低的特征，通過支持向量回歸進行分類，進行四重交叉驗證，得到理想的實驗數據。

2 實驗概述

2.1 數據集

為進行實驗，需要交叉驗證數據集，為驗證新算法的有效性，需使用與先前實驗相同的數據集，本文所使用的數據集為SP39［6］，該數據集來源于UniProtKB/Swiss-Prot，UniProtKB/Swiss-Prot是高質量的、手工注釋的、非冗余的數據集，SP39包含446條蛋白質序列，其中含有2，3，4，5個蛋白質鏈內二硫鍵數目的蛋白質序列數目依次為156，146，99，45。所有的蛋白質序列二硫鍵數目均不超過5個。

2.2 特征提取

2.2.1 位置特異得分矩陣（PSSM）

蛋白質進化信息是從蛋白質序列中獲PSSM矩陣，廣泛應用于其他領域，例如蛋白質功能預測與跨膜結構預測等，需要使用 PSI-BLAST［7］，滑動窗口大小選取為13，需要將兩個可能成鍵的半胱氨酸組合為樣本的PSSM特征。因此，PSSM的特征維數為520。

2.2.2 二級結構特征（PSS）

先前許多實驗已經證明，蛋白質二級結構不僅對預測二硫鍵有重要意義，還應用于許多其他領域，例如綁定位點預測等。原始二級結構分為三類：螺旋（H）、折疊（S）以及無規則卷曲（C）。為獲取二級結構特征，可以將蛋白質數據上傳到相關服務器計算，也可以使用PSIPRED［8］。所獲得的數據每個氨基酸殘基形成三種原始二級結構的概率，其具有的特征維數為78。

2.2.3 半胱氨酸預測距離特征（PDBCR）

當前技術條件下，無法精確預測蛋白質三維結構。通過Modeller［9］等3D結構預測軟件，將蛋白質序列與模板序列比對，利用同源建模算法預測出三維結構，獲得每個氨基酸殘基的三維空間位置，進而計算半胱氨酸之間的歐氏距離。通常情況下，兩個半胱氨酸歐式距離越小，其構成二硫鍵的概率越高。

2.2.4 關聯突變特征（CM）

兩個半胱氨酸如果能夠形成二硫鍵，那么這兩個半胱氨酸之間能夠發生強烈反應，它們之間相互依存，這種特性可以追溯到蛋白質進化信息。基于以上分析，Rubinstein與Fiser提出了通過關聯突變分析預測二硫鍵的形成，在他們提出的算法中，采用了相同標準，將所有的半胱氨酸對編碼為區間［0，1］的實數，詳細的算法參見相關文章［10］。

2.2.5 半胱氨酸序列距離特征（DOC）

半胱氨酸序列距離由Tsaietal首次提出，DOC通過以下公式對每個參與構鍵的半胱氨酸編碼：

其中，i和 j分別為半胱氨酸在蛋白質序列上的位置。

DOC特征需要標準化，其中的標準化方法有DOCL，DOCmax，Doclog，分別利用蛋白質鏈長度，數據集最大蛋白質鏈長度以及對數對特征進行標準化，經過測試，Doclog為最有效的方法，因此本文將采用Doclog進行歸一化處理，具體算法如下

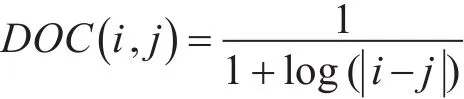
其中，i和 j分別為半胱氨酸在蛋白質序列上的位置。

綜上所述，將采用的局部特征組合為特征向量后，所形成的維數為603，高維數據不僅帶來計算上的不便，也有許多冗余信息，需要進行特征選擇。

2.3 費舍得分

特征選擇已被廣泛應用于生物信息學，其目的是從原始特征空間中選取有區分性的特征，進而提高預測的準確性。常用的特征選擇方法有方差得分，拉普拉斯得分，費舍得分，通過實驗證明，費舍得分效果最好。

費舍得分算法是監督學習的算法，廣泛應用于分類問題中。利用類標，找到對分類有重要作用的特征。當類內距離相對較小而類間距離相對較大時，這種算法顯著性水平較高［2］，假設具有C類，費舍得分計算如下

其中Ni為第i類樣本數目，為第i類樣本的m維特-征平均值，(σmi)2為第i類樣本的m維特征方差，為樣本所有數據m維特征的均值。

2.4 相關性選擇

線性相關指矢量空間中一個矢量可被其他矢量表示。當線性相關在矢量中存在時，其中至少一個矢量可以被其他矢量所代表，該矢量所含有的信息屬于冗余信息，相關性選擇便是剔除這些冗余信息［11］。為了得到不同特征之間的相關性，需要計算兩兩特征的線性相關系數，形成相關系數矩陣，該矩陣對角線元素均為1（任何特征與自身相關系數均為1），對該矩陣所有元素取絕對值，基于以下結論，可以進行相關性選擇：

1）相關系數絕對值越大，兩特征相關性越高；

2）某一特征相關系數較大值的數目越多，該特征所含信息越冗余；

計算線性相關系數，具體的計算過程如以下所示：

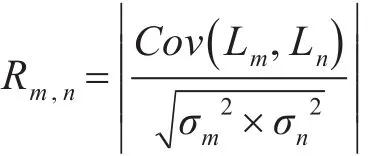
其中，Rm，n為兩個特征的相關系數絕對值，計算結果存儲到相關系數矩陣中。

通過相關性計算，可以獲得K×K（K為特征數目）的相關性矩陣，對于所獲得的矩陣，采用如下方式進行處理：

1）指定需要刪除的特征數目N；

2）尋找兩兩之間相關性最高的兩個特征；

3）對于1）選擇的兩個特征，尋找這兩個特征相關系數的次高值，二者之間的最大值所代表的特征為最終選擇的特征。

4）刪除2）中選擇的特征，此時特征數目為K=K-1，判斷是否 K=N，是則停止，否則重復2）。

利用最終形成的數據進行訓練與測試。

2.5 分類器選擇

在機器學習領域，提出過許多經典模型，例如貝葉斯回歸分析、隱馬爾科夫模型、支持向量回歸以及隨機森林等。其中本文采用了支持向量回歸。

支持向量機主要用于分類，是Cortes和Vapnik于1995年首先提出的，它在解決小樣本、非線性及高維模式識別中表現出許多特有的優勢，并能夠推廣應用到函數擬合等其他機器學習問題中。支持向量機方法是建立在統計學習理論的VC維理論和結構風險最小原理基礎上的，根據有限的樣本信息在模型的復雜性（即對特定訓練樣本的學習精度）和學習能力（即無錯誤地識別任意樣本的能力）之間尋求最佳折衷，以期獲得最好的推廣能力。

支持向量回歸是一種基于支持向量機的回歸模型，它得到的不是具體的分類，而是具體的值。與SVM訓練高維樣本相同，SVR需要選擇合適的核函數，本文選擇的是徑向基函數，采用LIBSVM進行支持向量回歸，對交叉驗證需要的最優參數，需要使用LIBSVM的網格搜索算法獲得。

2.6 評價標準

為描述模型的預測效果，我們采用了與前人相同的兩個指標：Qp和Qc其中，Qp為預測正確的二硫鍵占二硫鍵總數目的百分比，表示為

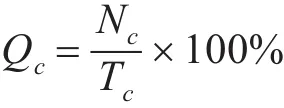
其中，Nc為預測正確的二硫鍵數目，Tc為樣本中的二硫鍵總數目。

另一個指標Qp是完全正確預測所有二硫鍵的蛋白質數目所占蛋白質樣本總數目的百分比，只有該蛋白質的所有二硫鍵均被正確預測時，該蛋白質才被認為正確預測，Qp的計算方法如下

其中，Np為正確預測的蛋白質數目，Tp為樣本蛋白質總數目。

2.7 工作流程

預測二硫鍵的工作流程如圖1所示，整個預測過程如下所示：

1）從蛋白質序列中獲取含有PSSM，PSS，CM，DOC，PDBCR特征的特征向量；2）對特征向量通過費舍得分進行特征選擇；3）對特征選擇后的特征子空間進行線性得分計算；

4）利用隨機森林回歸模型與支持向量回歸對處理后的數據進行四重交叉驗證；

5）預測關聯模式，其中令P為所有的關聯模式數目，第i種模式的得分計算方法如下

其中，B為半胱氨酸配對的數目，ppcpj為第 j對半胱氨酸對的構鍵概率。

最終，對i個模式，選取最大的值，該值代表的模式即為所求的最終結果：

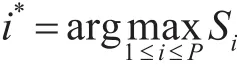
以圖1為例，對于二硫鍵數目為2的蛋白質，共有6組不同的半胱氨酸對形成3種不同模式，由于C1與C2，C3與C4的概率和為所有模式最大值，因此預測的半胱氨酸模式為(C1_C2，C3_C4)。

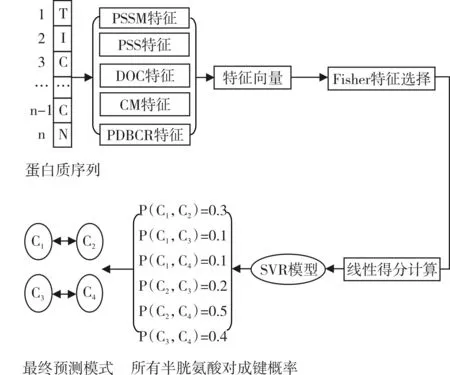
圖1 實驗流程圖

3 實驗結果

3.1 對特征進行相關性選擇可以有效提高預測精確度

該部分研究特征選擇與相關度選擇對預測結果的影響，對選用的SP39數據，對每重數據計算特征費舍得分然后取均值并排名，選取費舍得分較高的特征作為特征子空間進行相關性選擇，特征選擇數目從100取至500，特征選擇與相關性選擇每次實驗區間均取為50，對每次處理后的數據均進行4重交叉驗證，然后對剩余特征再次進行相關性選擇，重復進行，直到剩余特征達到50，記錄每次實驗數據。

表1和表2分別為通過采用4重交叉驗證進行預測時，通過特征選擇與線性選擇不同的維數后所Qc與Qp預測結果。

表1 Qc預測結果

在表1和表2中，第一列的特征數目為通過費舍得分保留的特征數目，第一行的特征數目為通過相關性選擇刪除的特征數目，由于相關性選擇在特征選擇之后進行，因此只有特征選擇的數目大于相關性選擇刪除特征的數目時才可以進行實驗。

表2 Qp預測結果

通過表1和表2可知，特征選擇與相關性選擇能夠提高預測的效果。在首先特征選擇維數為450，然后刪除相關度排名前200的特征，最終剩余250維特征時，兩項指標均取得最大值，分別為0.831與0.794，在特征選擇過程中，并非選擇數目越高結果越優，在特征數目超過450時，無論是Qp還是Qc值均下降，而相關度剔除的特征到達一定量時預測效果達到最佳，超過該數值，有效信息不足，預測結果同樣變差。

3.2 與其他結果比果

表3為本文算法與先前實驗結果對比，通過與前人實驗比較，本文結果在Qp上整體提高3.4%，在Qc上整體提高3.1%，在鏈內二硫鍵數目為2，3，4的情況下，實驗整體提高較為明顯，而二硫鍵數目為5的情況下效果反而變差，因此，本文的提出的通過提取蛋白質特征，進行費舍得分選擇以及相關性選擇，最終利用SVR進行交叉驗證的算法，對預測二硫鍵模式是有效的。

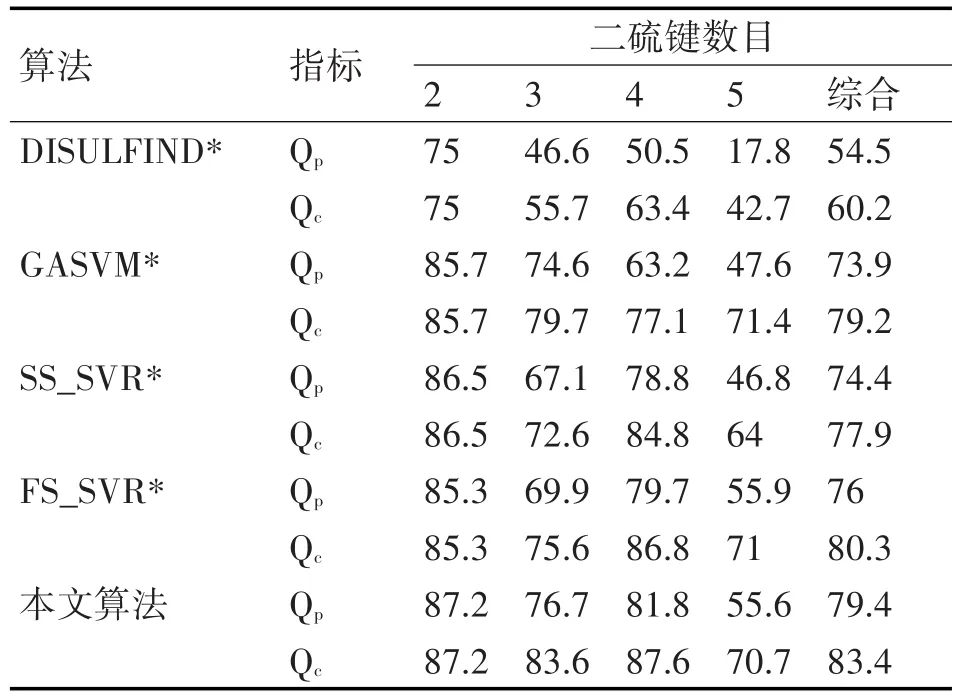
表3 多種算法比較

4 結語

本文之所以能夠得到更加準確的預測結果，主要得益于：

1）3D預測功能的改進，能夠得到更準確的半胱氨酸3D結構特征；

2）Swiss-Prot（www.ebi.ac.uk/swissprot）不斷更新數據集，所獲取的蛋白質進化信息更加完善，PSI-BLAST搜索的結果更加精確；

3）將特征進行相關性計算，使特征更具區性分性，模型訓練速度更快，預測精度更高。

本文所提出的相關性選擇算法，不僅僅可應用于生物信息學，可廣泛應用于其他分類問題。

未來的工作包括以下幾個方向：

1）尋找新的特征提高預測的準確性；

2）通過提出更優的算法預測鏈內二硫鍵數目更多（超過5個）的二硫鍵模式；

3）除鏈內二硫鍵外，利用機器學習的方法，對鏈間二硫鍵進行預測。

［1］Inaba K，Murakami S，Suzuki M，et al.Crystal structure of the DsbB-DsbA complex reveals a mechanism of disulfide bond generation［J］.Cell，2006，127（4）：789-801.

［2］Zhu L，Yang J，Song J N，et al.Improving the accuracy of predicting disulfide connectivity by feature selection［J］.Journal of computational chemistry，2010，31（7）：1478-1485.

［3］Tsai C-H，Chen B-J，Chan C-H，et al.Improving disulfide connectivity prediction with sequential distance between oxidized cysteines［J］.Bioinformatics，2005，21（24）：4416-4419.

［4］孫德山.支持向量機分類與回歸方法研究［J］.中南大學學報，2004，35（6）：13-15.SUN Deshan.Research on Support Vector Machine Classification and Regression Method［J］.Journal of Central South Oniversity，2004，35（6）：13-15.

［5］李欣海.隨機森林模型在分類與回歸分析中的應用［J］.應用昆蟲學報，2013，50（4）：1190-1197.LI Xinhai.Application of Random Forest Model in Classification and Regression Analysis［J］.Chinese Journal of Applied Entomology，2013，50（4）：1190-1197.

［6］Fariselli P，Casadio R.Prediction of disulfide connectivity in proteins［J］.Bioinformatics，2001，17（10）：957-964.［7］Sch?ffer A A，Aravind L，Madden T L，et al.Improving the accuracy of PSI-BLAST protein database searches with composition-based statistics and other refinements［J］.Nucleic acids research，2001，29（14）：2994-3005.

［8］Jones D T.Protein secondary structure prediction based on position-specific scoring matrices［J］.Journal of molecular biology，1999，292（2）：195-202.

［9］Webb B，Sali A.Comparative protein structure modeling using Modeller［J］.Current protocols in bioinformatics，2014，32（5）：1-6.

［10］Rubinstein R，Fiser A.Predicting disulfide bond connectivity in proteins by correlated mutations analysis［J］.Bioinformatics，2008，24（4）：498-504.

［11］張遠達.線性代數原理［M］.上海：上海教育出版社，1980.216-235.ZHANG Yuanda.Linear Algebra Principles［M］.Shanghai：Shanghai Education Press，1980.216-235.

Predicting Disulfide Connectivity Based on Correlation Coefficients Selection

LIU Kun
（School of Computer Science and Engineering，Nanjing University of Science and Technology，Nanjing 210094）

Disulfide connectivity is one of significant protein structural characteristic.Previous prediction methods usually used support vector regression，which didn't consider the correlation between different features.According to traditional prediction methods，based on fisher score，this paper calculated correlation coefficient of each pair of features after feature selection，then deleted the features with high correlation coefficient.Based on the rest features，support vector regression was used to train model and test.4-fold validation was used on our benchmark dataset to gain a hopeful result comparing with previous results.

bioinformatics，disulfide bond，support vector regression，correlation coefficient，feature selection

TP311

10.3969/j.issn.1672-9722.2017.11.003

Class Number TP311

2017年5月8日，

2017年6月23日

國家自然科學基金項目（編號：61373062，61371040）資助。

劉坤，男，碩士，研究方向：模式識別。