基于多維度空間耦合的六足機器人步態規劃

艾青林 阮惠祥 陳教料 應申舜

浙江工業大學特種裝備制造與先進加工技術教育部/浙江省重點實驗室，杭州，310014

基于多維度空間耦合的六足機器人步態規劃

艾青林 阮惠祥 陳教料 應申舜

浙江工業大學特種裝備制造與先進加工技術教育部/浙江省重點實驗室，杭州，310014

針對現有機身工作空間求解算法不適用于非平坦地形下六足機器人步態規劃的問題，提出一種基于多維度空間耦合算法的機身工作空間求解方法，并將其應用于機器人在非平坦地面運動的步態規劃中。將機身工作空間分為三個子空間，解析三個子空間邊界方程，耦合得出機身工作空間，在此基礎上，解析機身位姿與站立腿關節轉角之間的映射關系，完成機身運動規劃。仿真和樣機實驗結果對比表明：與采用傳統機身運動規劃算法的步態相比，所提方法能夠減小擺動腿足端偏移量和機身姿態角變化幅度，并且能夠保證機器人具有更高的步態穩定裕度，使機器人獲得更好的步態穩定性。

六足機器人；子空間耦合；機身工作空間；機身運動；步態規劃

0 引言

在多足機器人步態規劃中機身運動規劃對擺動腿足端理想落足點可達性、機器人穩定性以及步態效率等都有著重要的作用[1-2]。在多足機器人中，六足機器人具有冗余的肢體結構，能夠實現豐富的步態，因此被廣泛應用于戶外場景下作業[3-4]，而在戶外一些非平坦地面，六足機器人機身運動規劃具有更重要的作用，但目前關于四足機器人機身運動規劃的研究較多[5-8]，而對非平坦地面上六足機器人機身運動規劃的研究比較少。

機身運動規劃主要包括兩部分內容，分別是機身工作空間求解和機身位姿調整。其中，機身工作空間求解是機身運動規劃和機器人在非平坦地面上穩定運動的關鍵。目前，對多足機器人工作空間求解主要采用數值解析法[9-10]，這種方法在求解過程中涉及到較多的逆運動學解析，導致算法的計算效率不高，只適用于一些特定環境下的機器人步態規劃[11]，實際意義相對有限。文獻[12]采用蒙特卡羅方法對機器人工作空間進行求解，避免了機器人逆解問題，但這種方法不適用于六足機器人在非平坦地面的步態規劃。

在理想落足點和局部環境已知的情況下，要保證六足機器人步態穩定，其機身工作空間必須滿足三個條件：①滿足機身的運動約束；②保證擺動腿足端能夠落到理想的落足點；③確保機身具有足夠的穩定裕度。如果采用傳統的解析法求解機器人機身工作空間，求得的機身工作空間只能夠滿足第一個條件，要實現機器人的穩定步態就必須通過不斷地調整機身位姿來滿足后面兩個條件，這是一個復雜且不具確定性的過程，會影響機器人的步態效率，并且，基于這種方法設計的步態對地形的適應能力有限。

本文對機身運動的三個子空間進行求解，這三個子空間分別是機身運動約束空間K、理想落足點可達約束空間R以及機身穩定性約束空間B。當機身重心位于這三個子空間的交集空間中時，機器人運動滿足上面所述的三個條件，在此基礎上，對機身在理想工作空間中的位姿進行調整，完成六足機器人的機身運動規劃，在理想落足點已知的情況下，對六足機器人在非平坦地面的步態進行仿真分析和樣機實驗。

1 機器人運動學建模

本文所研究的六足機器人三維模型如圖1所示，圖中，尺寸單位為mm。根據D-H法建立圖2所示的六足機器人運動學模型，坐標系{W}、{C}分別為世界坐標系和機身坐標系。Li(i=1，2，3，4，5，6)分別為機器人的六條腿，因為每條腿的結構一樣，故以L2為例，建立腿部坐標系。坐標系{0}為根關節坐標系，H2為L2根關節離地高度，LF2為足端與根關節在水平地面上投影點之間的距離。坐標系{1}、{2}、{3}、{4}分別為基節、股節、脛節和足端坐標系，θ21、θ22和θ23分別為L2各關節轉角，l1、l2、l3分別為基節、股節和脛節的長度。

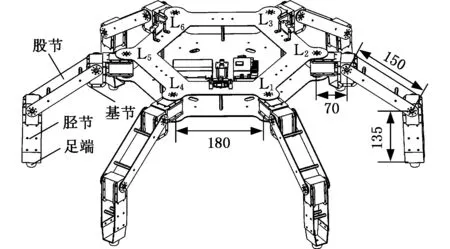
圖1 六足機器人三維模型Fig.1 The three-dimensional model of the hexapod robot

圖2 六足機器人運動學模型Fig.2 The kinematic model of the hexapod robot

根據圖2所示的運動學模型，結合D-H法可以求出足端2，A2在其根關節B2處的位置坐標為

B2pA2=[B2xA2B2yA2B2zA2]T=

(1)

式中，cθ=cosθ，sθ=sinθ，c(θ22+θ23)=cosθ22+cosθ23，s(θ22+θ23)=sinθ22+sinθ23，其余同理。

根據圖2中的幾何關系，求得H2和LF2的表達式為

(2)

根據文獻[13]所述的腿部逆運動學求解方法可以求得L2各關節轉角分別為

(3)

其中， Atan2(B2yA2，B2xA2)是一個計算arctan(B2yA2/B2xA2)的雙參數反正切函數，它通過B2yA2和B2xA2二者的符號來確定角的象限。t1、t2表達式如下：

a21、a22、a23和b21、b22、b23表達式如下：

2 基于多維度空間耦合的機身工作空間解析

本文提出的三個機身子空間分別滿足機身運動約束、擺動腿理想落足點可達約束以及機身穩定性約束，通過耦合三個子空間可求得機身工作空間。

2.1 機身運動約束空間K解析

圖3所示為單腿對機身運動的約束，圖中，點G為機身實時重心，機器人沿x軸正方向前進。用向量WpG=(WxG，WyG，WzG)T表示機身重心在世界坐標系中的位置坐標，結合圖3進行各個坐標間的向量運算，可得

(4)

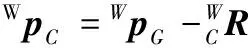
(5)

(6)

式中，α、β、γ分別為機身坐標系相對于世界坐標系的偏航角、俯仰角和橫滾角。

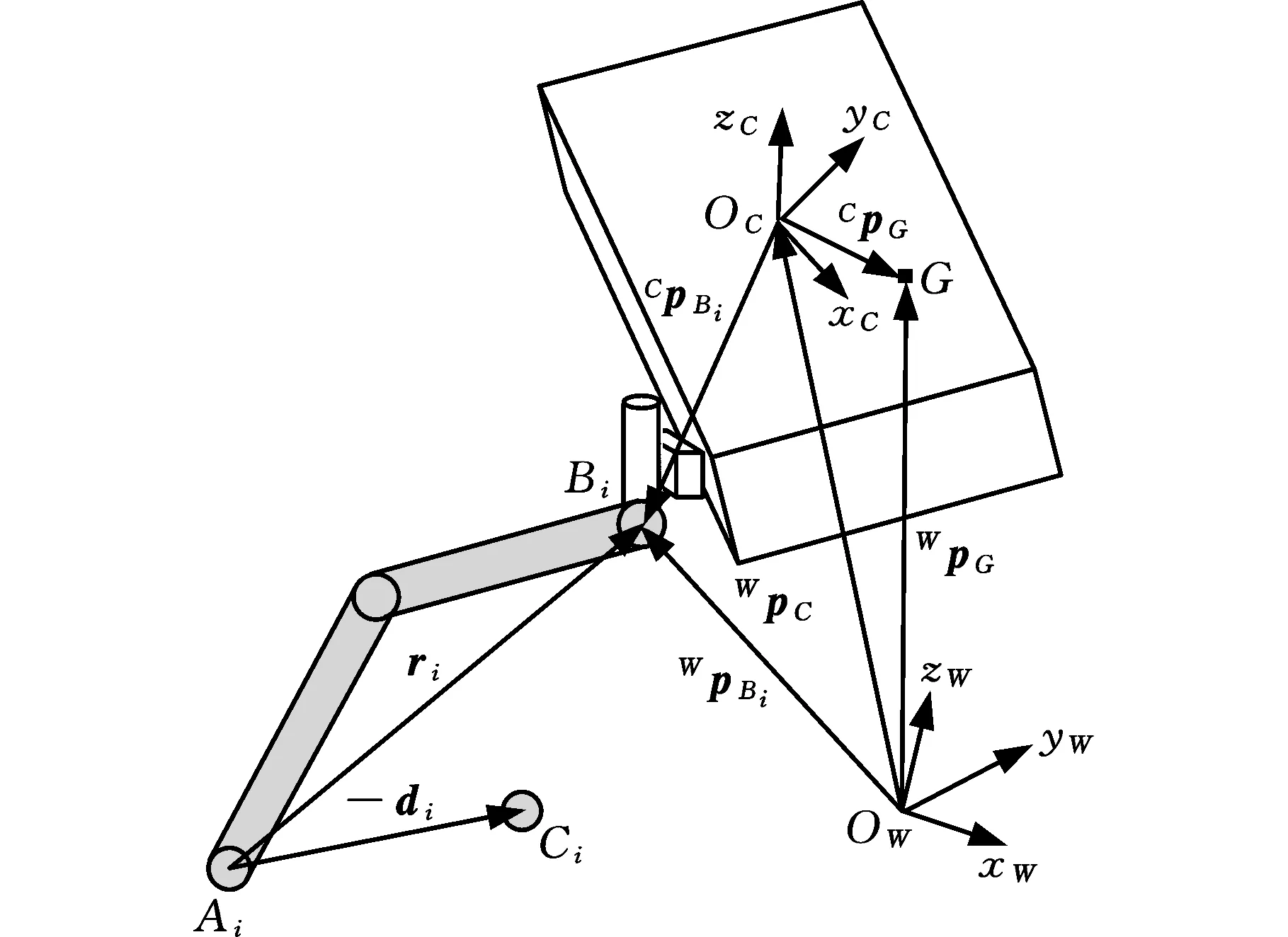
圖3 單腿對機身運動的約束Fig.3 The constrain of a leg on the body movement

聯立式(4)和式(5)，可得

(7)

式(7)兩邊同時減去向量WpAi得

(8)

式中，向量WpAi為足端在世界坐標系中的位置坐標。

圖3中，根關節到足端的距離‖ri‖可以表示為

(9)

其中，向量ri為單腿約束子空間的約束半徑，式(9)兩邊同時取平方，得

(10)

從式(10)可以看出，單腿約束子空間為兩個同心球體，其中，向量Wci為球心在世界坐標系下的位置坐標，可以表示為

(11)

根據式(11)，圖3中的向量di可以表示為

(12)

根據式(10)，耦合機器人腿部約束空間Ki，可得機身運動約束空間K：

K=K1∩K2∩K3∩K4∩K5∩K6

(13)

圖4為機身運動約束空間K在世界坐標系yz坐標面上的投影圖。

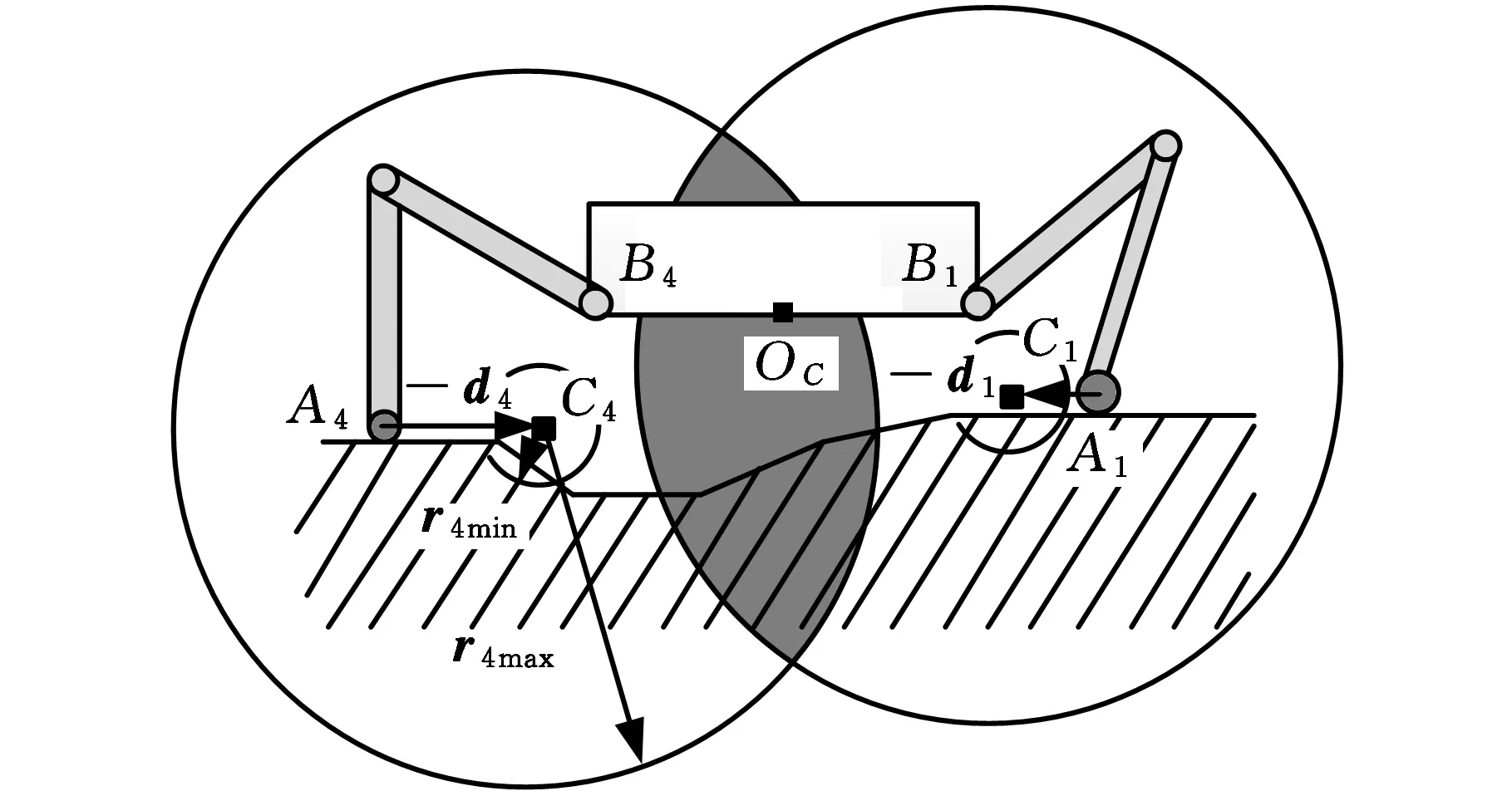
圖4 機身運動約束空間K在世界坐標系yz坐標面的投影Fig.4 The projection of the kinematic workspace of the body in the yz coordinate plane of the world coordinate system

圖4中，二個圖重疊部分為機身運動約束空間K，向量rimin為最小虛擬約束半徑，向量rimax為最大虛擬約束半徑，其表達式為

(14)

式中，LFi為足端與根關節在水平面上的垂直投影點之間的距離(圖2)；Hi為根關節與其在水平面上的垂直投影點之間的距離。

結合式(2)，代入關節轉角約束可以求得虛擬約束半徑的最大值和最小值。

2.2 機身理想落足點可達約束空間R解析

在非平坦地面下，六足機器人擺動腿理想落足點有限，因此，需要通過規劃機身位姿使得足端能夠準確地到達理想落足點。在2.1節求得的機身運動約束空間K中，許多機身位姿可能無法保證擺動腿足端能夠準確地到達理想落足點，因此，需要求解機身的另外一個子空間，即擺動腿理想落足點可達約束空間R。當機器人機身重心位于空間R和空間K的交集空間中時，機器人運動既能保證機身運動約束，也能保證擺動腿足端能夠準確地落到理想落足點。

根據機器人采用的步態方式，假設機器人有一條或者多條虛擬腿，并進一步假設這些虛擬腿已經落在理想落足點上。根據2.1節確定空間K的方法確定滿足虛擬腿約束空間K，即本節要求的理想落足點可達約束空間R，其表達式為

R=F1∩F2∩F3

(15)

式中，Fi(i=1,2,3)為虛擬擺動腿的運動約束空間。

式(15)求解了機器人在下個周期采用三角步態時的理想落足點可達約束空間R，此時虛擬腿的數量為3，如果機身在下個周期采用單步態或者四邊形步態，那么虛擬腿數量為1或者2。

2.3 機身穩定性約束空間B解析

當機身重心位于空間K和空間R的交集空間中時，六足機器人的運動既能滿足機身運動約束，又能保證機器人擺動腿足端能夠達到理想的落足點。然而，在非平坦地面，還必須確保機器人步態的穩定性。本文將機器人步態視為靜態步態，采用靜態穩定性判據來判斷機器人在非平坦地面下步態的穩定性。以六足機器人三角步態為例，其支撐多邊形如圖5所示。

圖5 三角步態支撐多邊形Fig.5 The support polygon of the tripod gait

支撐三角形各邊解析式如下：

(16)

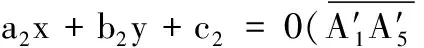
(17)

(18)

a1=y2-y1b1=x1-x2c1=x2y1-x1y2
a2=y3-y1b2=x1-x3c2=x3y1-x1y3
a3=y3-y2b3=x2-x3c3=x3y2-x2y3

式中，(x1，y1)，(x2，y2)，(x3，y3)分別代表足端A1、足端A3和足端A5在世界坐標系xy坐標面上的投影點坐標。

(19)

采用下式判斷機身重心在世界坐標系xy坐標面上的投影點是否落在支撐多邊形內：

SΔ1=SΔ2+SΔ3+SΔ4

(20)

根據式(20)可以求出子空間K和子空間R的交集空間中，哪些重心位置能夠確保機器人步態過程中保持穩定。

至此，機身三個工作子空間已經全部得出，對這三個子空間進行耦合，得機身工作空間：

W=K∩R∩B

(21)

以三角步態為例，機身工作空間W在世界坐標系xy平面下的投影如圖6所示。圖中，實線同心圓相交部分為機身運動約束空間K，虛線同心圓相交部分為擺動腿理想落足點可達約束空間R，實線三角形為穩定性約束空間B，三個子空間的交集空間為機身工作空間W。當機器人機身重心處于空間W中時，機器人運動既滿足機身運動約束，又能保證擺動腿足端可以落到理想點，還能確保步態的靜態穩定性。

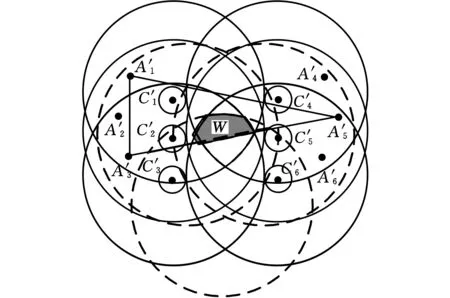
圖6 機身工作空間W在世界坐標系xy坐標面的投影Fig.6 The projection of the body workspace in the xy coordinate plane of the world coordinate system

3 機身位姿調整

機身位姿調整包括機身位置調整和機身姿態調整，其中，機身位置調整指的是當機身處于理想姿態時，解析機身重心位置與站立腿關節轉角之間的映射關系。用向量WpGO(WxGO,WyGO,WzGO)T和向量WpGD(WxGD,WyGD,WzGD)T分別表示機身重心在機身擺動前后相對于世界坐標系的位置坐標，則機身重心運動向量為WpGM(WxGD-WxGO,WyGD-WyGO,WzGD-WzGO)T。

根據相對運動原理，假設機身靜止，機身運動的過程可以看成是站立腿往相反方向擺動的過程，則站立腿足端擺動向量為

WpAiM=-WpGM

(22)

圖7a所示為機身位置調整前后站立腿足端擺動向量在世界坐標系、機身坐標系以及根關節坐標系下的位姿關系。圖7中，機身坐標系和根關節坐標系保持不變，AiO和AiD分別為機身位置調整前后的足端點，向量WpAiO和向量WpAiD分別為起始足端點和目標足端點在世界坐標系下的坐標，向量BipAiD為目標足端點在根關節坐標系下的位置，向量CpAiD為目標足端點在機身坐標系下的位置，圖中其余參量如前所述。

(a)機身位置調整前后各坐標系間的位姿關系

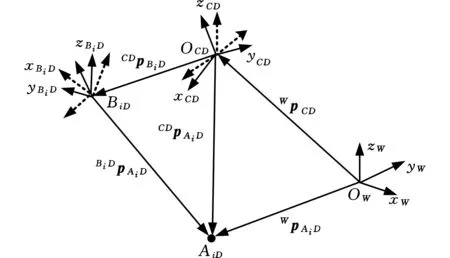
(b)機身姿態調整前后各坐標系間的位姿關系圖7 機身位姿調整前后各坐標系間的位姿關系Fig.7 The pose relationship between each coordinate system before and after the adjustment of body posture

結合圖7a可得目標足端坐標系相對于世界坐標系的位置坐標為

WpAiD=WpAiO-WpGM

(23)

根據各坐標系間的姿態轉換關系，可得目標足端坐標系相對于根關節坐標系的位置坐標為

(24)

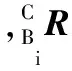
根據式(24)，結合式(3)，可以得出機身重心位置與站立腿關節角度間的映射關系。

當機身完成位置調整后，需對機身姿態進行調整，即當機身重心處于理想位置時，解析機身姿態與關節轉角之間的映射關系。圖7b為機身姿態調整前后站立腿足端在世界坐標系、目標機身坐標系以及目標根關節坐標系下的表示。圖中，位于機身坐標系和根關節坐標系處的虛線坐標軸為姿態調整前的機身坐標系和根關節坐標系，{OCD}和{OBiD}為機身姿態調整后的機身坐標系和根關節坐標系，向量BiDpAiD為機身位置調整后的目標足端點在目標根關節坐標系下的坐標，向量CDpAiD為機身位置調整后的目標足端點在目標機身坐標系下的位置，向量WpCD為目標機身坐標系在世界坐標系中的位置坐標，向量CDpBiD為目標根關節坐標系相對于機身坐標系的位置坐標，向量WpAiD為機身位置調整后的目標足端點在世界坐標系下的坐標，圖中其余參量如前所述。

結合圖7b，根據各坐標系間的姿態轉換關系，可得足端坐標系相對于目標根關節坐標系的位置坐標為

(25)

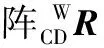
根據式(25)，并結合式(3)，可以得出機身姿態與站立腿關節角度間的映射關系。

4 仿真分析與樣機實驗

首先，通過MATLAB對不同姿態下的機身初始工作空間進行仿真，然后，通過MATLAB和ADAMS聯合仿真，對六足機器人在非平坦地形下的步態進行仿真，最后，通過樣機實驗驗證仿真結果的有效性。

4.1 機身初始工作空間仿真

本文研究的六足機器人機身和腿部各連桿尺寸如圖1所示。機身、基節、股節、脛節以及足端的質量分別為：mb=1000 g，m1=150 g，m2=200 g，m3=200 g，m4=50 g。受機械結構限制，腿部各關節轉角約束分別為：-π/3≤θ1≤π/3，-π/2≤θ2≤π/2，-π/2≤θ3≤π/2。根據式(14)，求得單腿虛擬約束半徑為：163 mm≤‖ri‖≤355 mm。

假設機器人處于初始狀態時，機身坐標系相對于世界坐標系的姿態角為α=0°、β=0°、γ=0°；各腿足端在世界坐標系中的位置分別為：A1(500，527，80)mm，A2(281，618，80)mm，A3(43，527，80)mm，A4(500，-51，80)mm，A5(280，-141，80)mm，A6(57，-51，80)mm；根關節在機身坐標系下的位置為：B1(156，90，0)mm，B2(0，180，0)mm，B3(-156，90，0)mm，B4(156，-90，0)mm，B5(0，-180，0)mm，B6(-156，-90，0)mm。令機器人各腿沿機身均勻分布，則機身重心與機身幾何中心重合，機身重心在機身坐標系下的位置坐標為CpG(0，0，0)mm；機器人下個步態采用三角步態，腿1、3、5為擺動相，理想落足點在世界坐標系中的位置分別為：R1(600，527，180)mm，R3(143，527，80)mm，R5(380，-141，80)mm；根據式(10)和式(11)，通過MATLAB對機身初始工作空間進行仿真計算，結果如圖8a所示，改變機身初始姿態，此時機身坐標系相對于世界坐標系的姿態為α=10°，β=10°，γ=10°，其余參數保持不變，機身工作空間如圖8b所示；再次改變機身初始姿態，此時機身坐標系相對于世界坐標系的姿態為α=15°、β=15°、γ=15°，其余參數保持不變，機身工作空間如圖8c所示。

(a)姿態角為0°

(b)姿態角為10°

(c)姿態角為15°圖8 不同姿態下的機身初始工作空間Fig.8 The initial body workspace with different orientation

當機身處于不同姿態時，機身虛擬約束半徑保持不變，均為163 mm≤‖ri‖≤355 mm；而機身單腿約束子空間球心位置不同，比如當機身初始姿態為α=0°，β=0°，γ=0°時，各個單腿約束子空間的球心位置分別為C1(337，39，80)mm，C2(344，437，80)mm，C3(281，438，80)mm，C4(199，437，80)mm，C5(213，39，80)mm，C6(280，39，80)mm；而當機身初始姿態為α=10°、β=10°、γ=10°時，各個單腿約束子空間的球心位置分別為C1(330，10，122)mm，C2(362，413，92)mm，C3(306，442，49)mm，C4(206，466，38)mm，C5(195，63，68)mm，C6(255，35，111)mm；虛擬單腿約束子空間球心位置也不同，當機身初始姿態為α=0°，β=0°，γ=0°時，虛擬單腿約束子空間的球心位置分別為C7(444，437，180)mm，C8(299，437，80)mm，C9(380，39，80)mm；當機身初始姿態為α=10°、β=10°、γ=10°時，各個虛擬單腿約束子空間的球心位置分別為C7(461，412，191)mm，C8(307，465，37)mm，C9(354，34，110)mm。即機身初始姿態的變化會引起機身運動約束空間K和理想落足點可達約束空間R變化，從而改變機身工作空間W，如圖8所示，并且，機身工作空間W隨著機身姿態角的增大而減小。

4.2 非平坦地面步態仿真

在理想落足點已知的前提下，通過MATLAB對機器人逆解進行求解，將得到的關節輸出位置角導入到ADAMS中，完成六足機器人在非平坦地面下的步態聯合仿真。

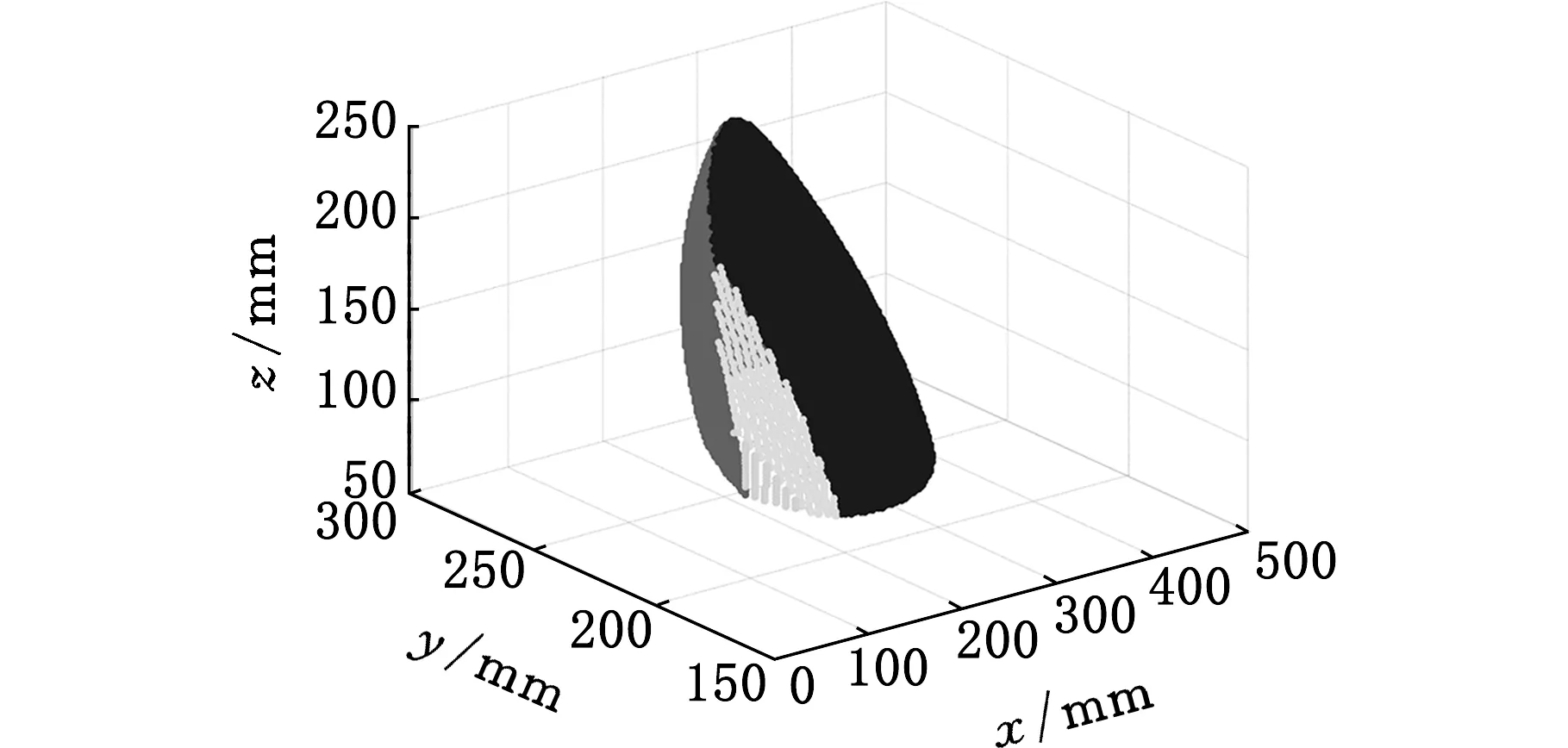
在機身運動規劃中，采用兩種不同的方法對機身工作空間進行求解:第一種方法是本文提出的多維度工作空間耦合求解方法，第二種方法是文獻[15]所述方法，即不考慮足端理想落足點可達約束和機身穩定性約束。將這兩種機身運動規劃方法分別運用于非平坦地面下的步態仿真。在ADAMS中的仿真環境如圖9所示。圖9中，參數L=500 mm，d=30 mm，H1=80 mm，H2=180 mm，W1=900 mm，W2=450 mm。機器人機身初始姿態角為α=0°，β=0°，γ=0°，初始位置足端在世界坐標系下的坐標分別為A1(500，527，80)mm，A2(281，618，80)mm，A3(43，527，80)mm，A4(500，-51，80)mm，A5(280，-141，80)mm，A6(57，-51，80)mm，機身初始工作空間如圖8a所示。

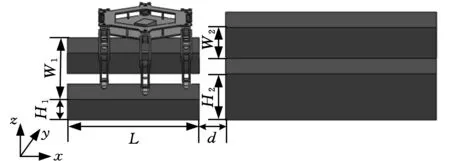
圖9 機器人步態仿真環境Fig.9 The gait simulation circumstance of the hexapod robot

單步態周期時序圖見圖10，圖10中，機器人采用三角步態，白框代表支撐相，黑框代表擺動相，灰框代表調整相，擺動相、支撐相和調整相時間都設為0.2 s，步幅設為100 mm，足端與地面之間的靜摩擦因數和動摩擦因數分別為0.3和0.2，仿真時間設為4 s，共5個步態周期。

圖10 單個周期步態時序圖Fig.10 The sequence chart of a period gait

兩次仿真過程中，機器人各足端與理想落足點之間的偏移量不同，以足端4為例，圖11a和圖11b為足端4在世界坐標系下沿x軸和y軸的軌跡，仿真1采用本文提出的方法規劃機身運動，仿真2采用文獻[15]方法規劃機身運動。

(a)足端4沿世界坐標系x軸軌跡

(b)足端4沿世界坐標系y軸軌跡圖11 足端4沿世界坐標系x軸和y軸的軌跡Fig.11 The path of the footend along the x and y axis of the world coordinate system

本文所提出的機身工作空間求解方法考慮了足端理想落足點可達的問題，因此在步態過程中，足端橫向和縱向偏移量相對較小，足端4在步態仿真過程中，5次作為擺動相，時間分別是0.6～0.8 s、1.4～1.6 s、2.2～2.4 s、3.0～3.2 s、3.8～4.0 s，對應的5個理想落足點分別為(600，-51，180)mm，(700，-51，180)mm，(800，-51，180)mm，(900，-51，180)mm， (1000，-51，180)mm。仿真1足端4最終落足點分別為(605，-48，180)mm，(708，-45，180)mm，(810，-45，180)mm，(910，-43，180)mm，(1011，-41，180)mm。仿真2足端4最終落足點分別為(605，-45，180)mm，(714，-38，180)mm，(822，-29，180)mm， (930，-19，180)mm，(1039，-8，180)mm。對比兩次仿真，仿真1中，足端4單步態周期最大縱向和橫向偏移量分別為11 mm和10 mm，仿真2中，足端4單步態周期最大縱向和橫向偏移量分別為39 mm和43 mm，即仿真1足端x軸和y軸偏移量分別是仿真2的28%和25%，并且，仿真2中足端1的橫向偏移量呈現大幅度的累加趨勢，如果機器人繼續直行或者W2的值減小，那么機器人將偏離理想軌跡，然后從地面上失穩跌倒。

機身重心沿世界坐標系x軸和y軸軌跡如圖12所示。機器人各足端的偏移會最終導致機器人步態軌跡的偏離，圖12中，仿真1機身重心最終縱向和橫向偏移量分別為9 mm和14 mm；仿真2機身最終縱向和橫向偏移量分別為23 mm和34 mm，即仿真1機身重心沿x軸和y軸偏移量分別是仿真2機身重心沿x軸和y軸偏移量的39%和40%。

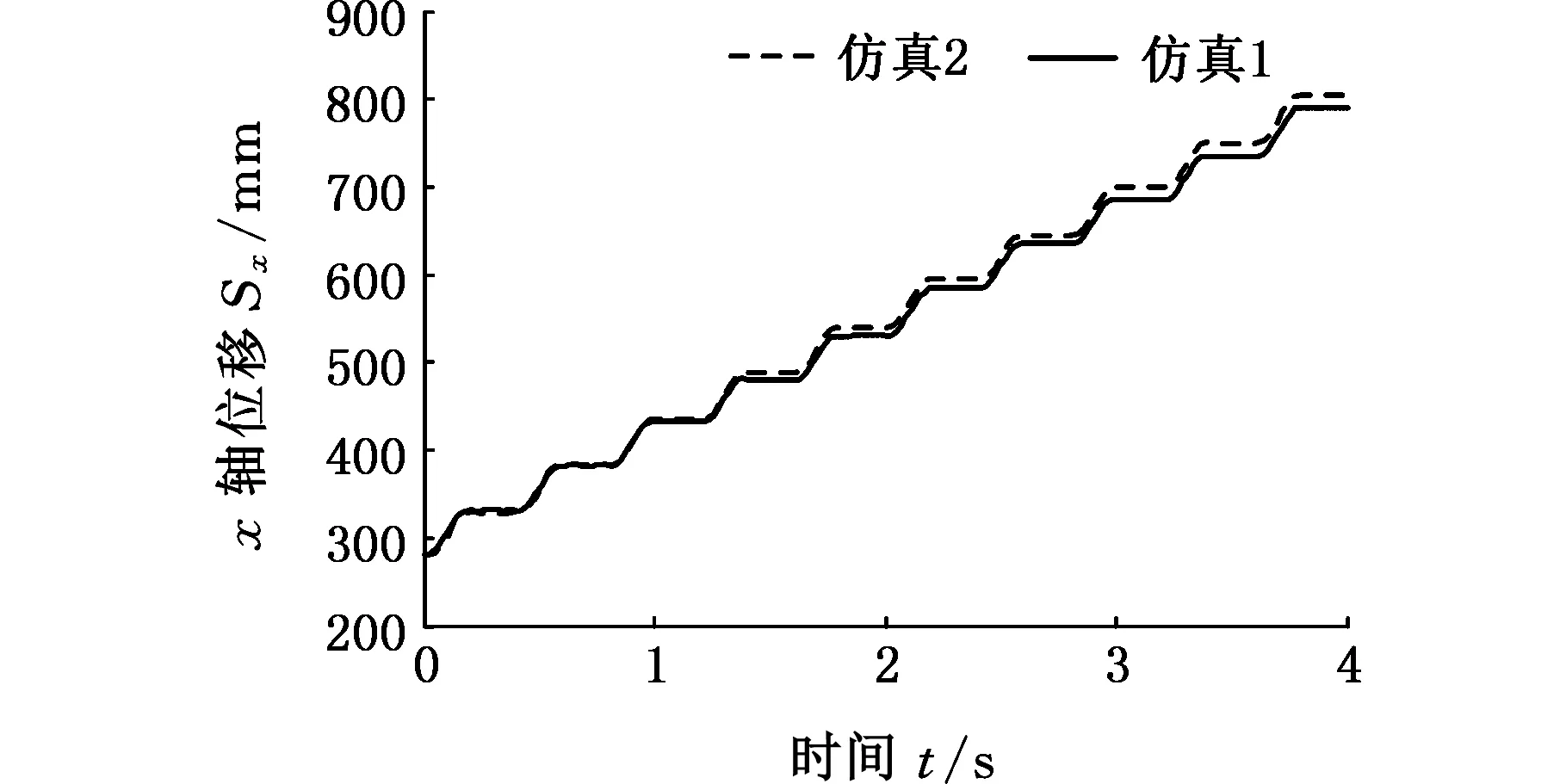
(a)機身重心沿世界坐標系x軸軌跡

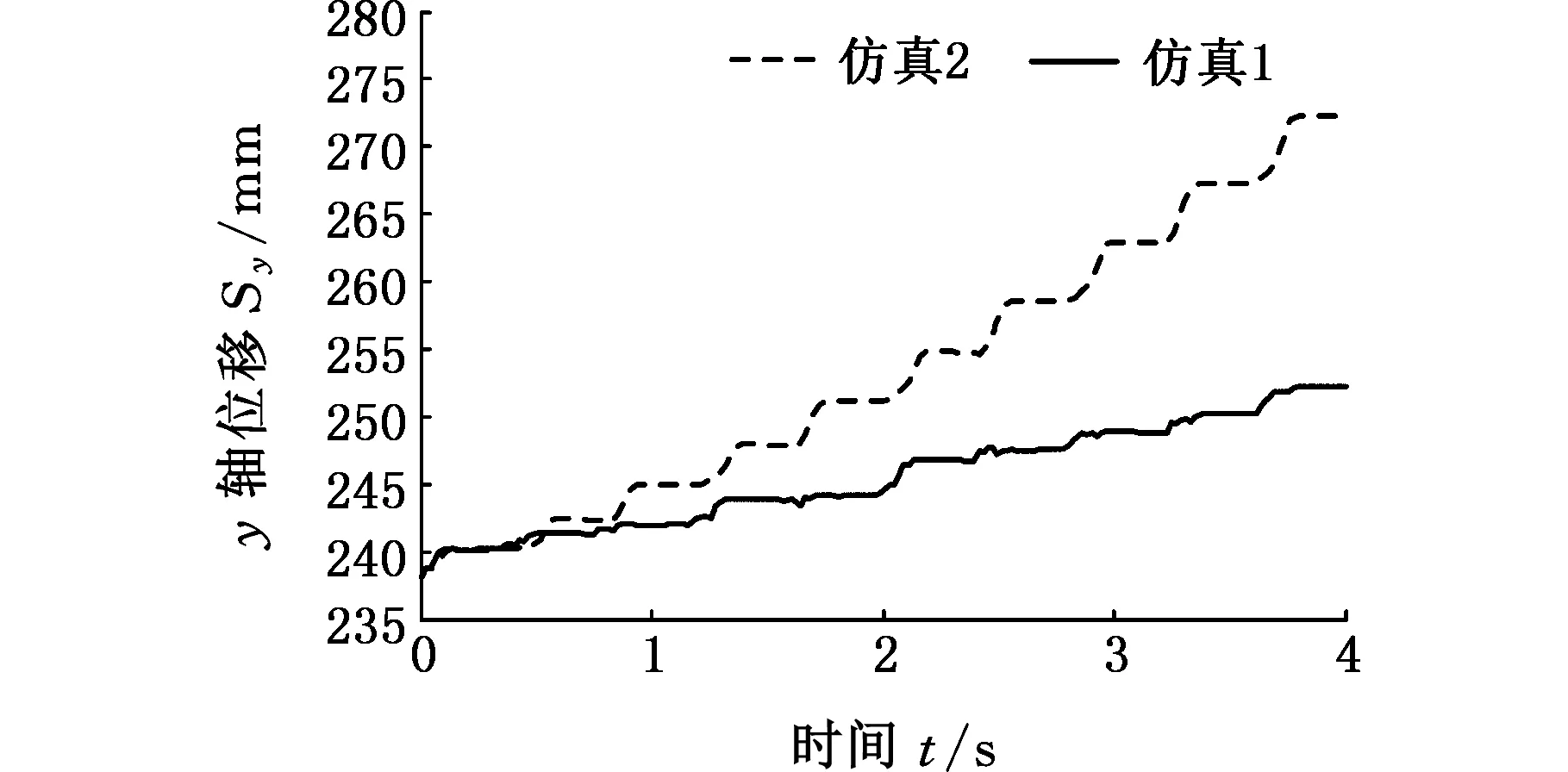
(b)機身重心沿世界坐標系y軸軌跡圖12 機身重心沿世界坐標系x軸和y軸的軌跡Fig.12 The path of the center of gravity of the body along the x and y axis of the world coordinate system

穩定裕度是判斷機器人靜態步態穩定性的一個重要指標，圖13為機器人在步態過程中穩定裕度Sm的變化曲線。

圖13 機器人穩定裕度SmFig.13 The stable margin of the hexapod robot

機器人的步態，在運動狀態發生變化時最容易發生失穩，如0.2～0.4 s，機器人由調整相變為擺動相，站立腿數量減少，Sm的值也發生了明顯的變化，對比兩次仿真，仿真1中，Sm的值由163 mm變為64 mm，減小了99 mm，仿真2中，Sm的值由166 mm變為30 mm，減小了136 mm，由于仿真1在機身工作空間求解過程中考慮了機身穩定性約束，所以Sm的減小量僅為仿真2的72%，并且隨著地形崎嶇度的增大這個比例將會進一步減小，如果不作出調整，仿真2的機器人在步態過程中很有可能會出現傾翻的情況。

機器人機身的俯仰角和橫滾角反映了機身運動的平穩性，圖14為機器人步態過程中，機身坐標系相對于世界坐標系的俯仰角β和橫滾角γ的變化曲線。

(a)機身相對世界坐標系俯仰角β

(b)機身相對世界坐標系橫滾角γ圖14 機身相對世界坐標系姿態角Fig.14 The angle of orientation of the body in the world coordinate system

圖14中，仿真1俯仰角和橫滾角的變化范圍分別為-1.9°～2.9°和-1°～1.5°，仿真2俯仰角和橫滾角的變化范圍分別為-8.2°～3.8°和0.1°～4.1°，仿真1在機器人步態過程加入了機身調整相，并且在機身位姿調整過程中考慮了機身實時重心位置變化的問題，提高了機身姿態調整的準確性，保證了姿態調整后機身俯仰角和橫滾角的變化幅度更小，調整過后的俯仰角和橫滾角的變化范圍僅為仿真2俯仰角和橫滾角變化范圍的40%和60%。

4.3 樣機實驗

通過所設計的樣機實驗平臺，對本文提出的步態規劃方法進行了進一步的驗證。

4.3.1樣機搭建

本文所研究的六足機器人樣機如圖15所示，采用CM-700作為下位機主控板，用來驅動關節舵機和外部傳感器。CM-700理論上可以同時帶動255個舵機，各個舵機通過編程實現ID設置，板載5路485通信接口和4路TTL通信接口用來驅動關節舵機，6路外部設備通信接口用來驅動外部傳感器，可驅動的傳感器類型包括紅外傳感器、測距傳感器和接觸傳感器等；機器人每條腿各有3個關節，共18個關節，全部采用RX-24F舵機驅動，RX-24F舵機最大力矩可達2.4 N·m，和主控板之間通過485協議進行通信，舵機內置控制芯片，能夠實時反饋舵機的位置、電壓、力矩和角速度等信息；板載傳感器包括測距傳感器DMS-80以及陀螺儀傳感器，后續還將加上視覺傳感器和足端觸覺傳感器，其中，DMS-80傳感器的有效測距范圍為10～80 cm，在有效測距范圍內，其測距誤差可以控制在1%以內；陀螺儀傳感器能夠測得機身沿世界坐標系x軸和y軸的轉角位置和轉角速度。機身和腿部采用硬質鋁合金構造，整機質量在3 kg左右。

圖15 六足機器人實驗平臺Fig.15 The experimental platform of the hexapod robot

4.3.2實驗分析

在仿真的基礎上，增大地面不平坦度，將d設置為100 mm，W1設置為800 mm，將兩段路面設置為一個坡度角為6°的斜面，其余參數如圖9所示。機器人采用三角步態，步幅設置為150 mm，步態過程中，調整相、擺動相和支撐相的時間依舊都設為0.2 s，進行三個周期的步態，步態過程如圖16所示。0.4～0.6 s為機身調整相，此時，機身完成位姿調整，保證機器人下個運動狀態穩定裕度不出現大幅度下降，擺動相能夠達到理想的落足點，并且機身姿態角不出現大范圍波動。從圖16中可以看出，整個步態過程中，機器人足端位置沒有發生明顯的偏移，以足端4為例，在步態起始時，足端4距離路面左邊界距離為80mm，在整個步態過程中，足端4落足點與路面左邊界距離一直保持在80mm左右，在步態結束時，這個距離為85mm；同時，機器人在步態過程中，機身姿態也沒有發生明顯的變化，機器人從起始位置到終止位置，機身一直保持直行狀態，實現了機器人在非平坦地面下穩定的步態過程，從而證明了所提步態規劃方法的有效性。

(a)t=0 (b)t=0.4 s

(c)t=0.6 s (d)t=0.8 s

(e)t=1.2 s (f)t=1.6 s

(g)t=2.0 s (h)t=2.4 s圖16 六足機器人樣機步態實驗Fig.16 The prototype gait experiment of the hexapod robot

5 結語

為了提高六足機器人在非平坦地面下步態的穩定性，本文提出了一種基于多維度工作空間耦合的方法求解機身工作空間，將其應用于非平坦地面下機器人的步態規劃中，并通過了仿真和樣機實驗驗證了所提方法的可行性。和采用傳統機身運動規劃方法的步態相比，本文所提的步態規劃方法具有如下創新點。

(1)在機身工作空間求解過程中，避免了復雜的機器人逆運動學求解，考慮了擺動腿理想落足點可達約束，保證了機器人在步態過程中，足端和機身重心橫向和縱向的偏移量僅為采用傳統步態規劃方法的28%、25%和39%、40%，提高了機器人步態的位移控制精度。

(2)在機身工作空間求解過程中，考慮到了機身穩定性約束，保證了機器人在步態過程中，當運動狀態發生變化時，穩定裕度Sm的減小量僅為采用傳統步態規劃方法的72%，提高了機器人步態的穩定性。

(3)驗證了當機身姿態角分別為0°、10°和15°時，機身工作空間相繼減小，由此，在步態過程中加入了調整相，對機身姿態進行了調整，并且，在機身運動規劃時，考慮到了實時重心位置變化，提高了機身運動規劃的準確性，調整過后的機身俯仰角β和橫滾角γ變化幅度分別減小了近60%和40%，提高了機身的運動平穩性。

在本文中，對機器人機身運動規劃時，沒有對機身初始位姿進行優化，在后續的研究工作中，將對機器人機身相對于世界坐標系的位姿進行優化，進一步提高步態的穩定性，減小步態過程中足端相對理想落足點的偏移量。

[1] HAUSER K K, BRETL T, LATOMBE J C, et al. Motion Planning for Legged Robots on Varied Terrain [J]. International Journal of Robotics Research, 2008, 27(11): 1325-1349.

[2] ESTREMERA J, COBANO J A, SANTOS P G D. Continuous Free-crab Gaits for Hexapod Robots on a Natural Terrain with Forbidden Zones: an Application to Humanitarian Demining [J]. Robotics and Autonomous Systems, 2010, 58(5): 700-711.

[3] ZHANG He, LIU Yubin, ZHAO Jie, et al. Development of a Bionic Hexapod Robot for Walking on Unstructured Terrain [J]. Journal of Bionic Engineering, 2014, 11(2): 176-187.

[4] 趙龍海. 六足步行機器人自然地形下全方位運動規劃策略研究 [D]. 哈爾濱: 哈爾濱工業大學, 2013.

ZHAO Longhai. Research on Omnidirectional Motion Planning of the Hexapod Walking Robot on Natural Terrain [D]. Harbin: Harbin Institute of Technology, 2013.

[5] KOLTER J Z, NG A Y. The Stanford Little Dog: a Learning and Rapid Replanning Approach to Quadruped Locomotion [J]. International Journal of Robotics Research, 2011, 30(2): 150-174.

[6] NEUHAUS P D, PRATT J E, JOHNSON M J. Comprehensive Summary of the Institute for Human and Machine Cognition’s Experience with Little Dog [J]. International Journal of Robotics Research, 2011, 30(2): 216-235.

[7] ESTREMERA J, SANTOS P G D.Generating Continuous Free Crab Gaits for Quadruped Robots on Irregular Terrain [J]. IEEE Transactions on Robotics, 2006, 21(6): 1067-1076.

[8] KALAKRISHNAN M, BUCHLI J, MISTRY M, et al. Learning, Planning, and Control for Quadruped Locomotion over Challenging Terrain [J]. International Journal of Robotics Research, 2011, 30(2): 236-258.

[9] 趙杰, 王衛忠, 蔡鶴皋. 可重構機器人工作空間的自動計算方法 [J]. 天津大學學報, 2006, 39 (9): 1082-1087.

ZHAO Jie, WANG Weizhong, CAI Hegao. Algorithms for Automatically Determining Workspace of Reconfigurable Robots [J]. Journal of Tianjin University, 2006, 39(9): 1082-1087.

[10] LOC V G, KOO I M, TRAN D T, et al. Improving Traversability of Quadruped Walking Robots Using Body Movement in 3D Rough Terrains [J]. Robotics and Autonomous Systems, 2011, 59(12): 1036-1048.

[11] VERNAZA P, LIKHACHEV M, BHATTACHARYA S, et al. Search-based Planning for a Legged Robot over Rough Terrain [C]//IEEE International Conference on Robotics and Automation. Kobe, Japan, 2009: 12-17.

[12] 曹毅, 王樹新, 李群智. 基于隨機概率的機器人工作空間及其解析表達[J]. 組合機床與自動化加工技術, 2005 (2):1-4.

CAO Yi, WANG Shuxin, LI Qunzhi. Generation of Manipulator Workspace Boundary Geometry Using the Probabilistic Method and Its Analytical Description [J]. Modular Machine Tool&Automatic Manufacturing Technique, 2005 (2):1-4.

[13] 李滿宏, 張建華, 張明路. 新型仿生六足機器人自由步態中足端軌跡規劃[J]. 中國機械工程, 2014, 25(6):821-825.

LI Manhong, ZHANG Jianhua, ZHANG Minglu. Foot Trajectory Planning for a Hexapod Biomimetic Robot Using Free Gait [J]. China Mechanical Engineering, 2014, 25(6):821-825.

[14] SANDOVAL-CASTRO X Y, CASTILLO-CASTANEDA E, LOZANO-GUZMAN A A. Hexapod Walking Robot CG Analytical Evaluation [J]. Springer International Publishing, 2014, 8917: 309-319.

[15] 李滿宏, 張明路, 張建華, 等. 基于運動相對性的六足機器人機體運動規劃 [J]. 中國機械工程, 2015, 26(3):313-318.

LI Manhong, ZHANG Minglu , ZHANG Jianhua, et al.Body Motion Planning for a Hexapod Robot Based on Relative Motion [J]. China Mechanical Engineering, 2015, 26(3):313-318.

GaitPlanningofaHexapodRobotBasedonMulti-dimensionalSpaceCoupled

AI Qinglin RUAN Huixiang CHEN Jiaoliao YING Shenshun

Key Laboratory of E&M,Ministry of Education & Zhejiang Province,Zhejiang University ofTechnology,Hangzhou,310014

The existing algorithms to compute the body workspace were not suitable for the gait planning of a hexapod robot on the uneven terrains. To overcome this problem, a calculation method of the body workspace of a hexapod robot was introduced based on multi-dimensional space coupled herein. Then, the method was applied to the gait planning on the unseven terrains. Three subspaces of the body and the boundary equation of these subspace were presented, and then, these subspaces were coupled to get the body workspace. Based on the body workspace, in order to obtain the relationship among the postures of the body and the joint angles of standing legs, the algorithm of the body postures was solved. The simulation and experimental results show that compared with the existing planning methods the gait planning introduced herein may guarantee the footend reaching the desired foot point precisely and reduce the rangeability of the attitude angles of the body, which may ensure the hexapod robot walking on the uneven terrains stably.

hexapod robot; subspace coupled; body workspace; body movement; gait planning

TP242

10.3969/j.issn.1004-132X.2017.23.009

2016-12-16

NSFC-浙江兩化融合聯合基金資助項目(U1509212)；國家自然科學基金資助項目(51275470)；浙江省高等學校中青年學科帶頭人學術攀登項目(pd2013019)

(編輯王艷麗)

艾青林，男，1976年生。浙江工業大學機械工程學院教授、博士研究生導師。主要研究方向為多足機器人控制技術、鋼帶并聯機器人技術、建筑鋼結構探傷機器人技術等。發表論文50余篇。授權專利30多項。E-mail：aqlaql@163.com。阮惠祥，男，1991年生。浙江工業大學機械工程學院碩士研究生。陳教料，男，1979年生。浙江工業大學機械工程學院副教授。應申舜，男，1978年生。浙江工業大學機械工程學院講師。