基于局部密度的快速離群點檢測算法

鄒云峰,張 昕,宋世淵,倪巍偉

(1.國網江蘇省電力公司 電力科學研究院,南京 210036; 2.東南大學 計算機科學與工程學院,南京 211189) (*通信作者電子郵箱2293515844@qq.com)

基于局部密度的快速離群點檢測算法

鄒云峰1,張 昕1,宋世淵2*,倪巍偉2

(1.國網江蘇省電力公司 電力科學研究院,南京 210036; 2.東南大學 計算機科學與工程學院,南京 211189) (*通信作者電子郵箱2293515844@qq.com)

已有的密度離群點檢測算法LOF不能適應數據分布異常情況離群點檢測，INFLO算法雖引入反向k近鄰點集有效地解決了數據分布異常情況的離群點檢測問題，但存在需要對所有數據點不加區分地分析其k近鄰和反向k近鄰點集導致的效率降低問題。針對該問題，提出局部密度離群點檢測算法——LDBO，引入強k近鄰點和弱k近鄰點概念，通過分析鄰近數據點的離群相關性，對數據點區別對待；并提出數據點離群性預判斷策略，盡可能避免不必要的反向k近鄰分析，有效提高數據分布異常情況離群點檢測算法的效率。理論分析和實驗結果表明，LDBO算法效率優于INFLO，算法是有效可行的。

離群點檢測;局部密度;強k近鄰點;弱k近鄰點;反向k近鄰點集

0 引言

離群點檢測(Outlier Detection)作為數據挖掘技術的重要研究領域之一,是從大量事物中發現少量與多數事物具有明顯區別的異常個體的過程[1]。離群點檢測在很多領域有著廣泛的應用前景，例如,電子商務中的欺詐行為、金融領域中信用卡惡意透支、網絡安全中的惡意攻擊、地震預報中的異常波形、網絡入侵抵御等。

離群點檢測技術由于其獨特的知識發現功能而得到了較深入的研究。近年來提出了一系列檢測方法,Johnson等[2]提出基于深度的算法, Knorr等[3]提出基于距離的算法FindAllOutsD,Breunig等[4]提出帶離群度的離群點檢測算法LOF(Local Outlier Factor),Papadimitirou等[5-13]提出LOCI(LOcal Correlation Integral)算法等。局部離群點檢測是離群點檢測的一個重要研究方向,文獻[11]針對LOF算法的不足,提出了基于反向k近鄰(ReversekNearest Neighbors, RkNN)的局部離群度判別方法INFLO(INFLuenced Outlierness),不同于LOF算法只考慮數據點的k近鄰,算法同時考慮數據點的反向k近鄰對數據點離群度的影響,從而避免數據分布異常情況下LOF算法可能出現的錯判。例如,圖1中,根據LOF算法對數據點離群度的定義,可能出現屬于聚類C2的數據點p的離群度高于數據點q和r的離群度,出現p比數據點q和r更易被判定為離群點的錯判現象。采用INFLO方法后,在分析p、q、r的k近鄰(k-Nearest Neighbors, KNN) 的同時,進一步分析各個數據點反向k近鄰。INFLO方法結合數據點p的反向k近鄰數據點對p的影響,可以得出p的離群度小于q和r的離群度的正確結果。

INFLO方法可以解決LOF算法不適應數據分布異常情況下離群點判定的缺陷,但仍然存在以下不足:

1)算法既要查詢生成每個數據點p的k近鄰,又要查詢p的反向k近鄰(RkNN),頻繁的RkNN查詢對算法的性能影響很大,盡管文獻[11]中采用R樹等索引結構來提高查詢效率,但并不能從根本上解決效率問題；另一方面,當數據集維度較高時,R樹等索引結構的效率比順序遍歷查詢還要差,也無法實現其提高效率的目的。

2)算法需要對每一個數據點的離群度進行分析計算,判斷其是否可能是離群點,導致時間開銷很大,大量反向k近鄰查詢加劇了這種負擔;實際數據集中,異常分布點僅占數據集的很小部分,例如圖1中,只有聚類C1和C2的邊緣點,以及諸如q和r這樣的數據點分布異常,對數據集中的大多數數據點(C1和C2中的數據點)無需分析其RkNN,就可以得出正確的離群判斷。

針對上述問題,本文提出一種基于局部密度的快速離群點檢測方法LDBO(Local Density Based Outlier detection),算法無需對數據集中所有數據點進行離群與否分析,在僅需對部分數據點計算反向k近鄰的情況下,有效地解決數據分布異常環境下離群點檢測問題。

圖1 數局分布異常情況

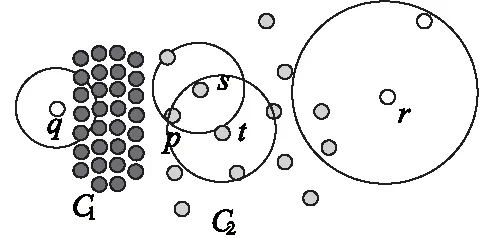
圖2 反向k近鄰分析實例

1 相關工作

1.1 LOF算法

基于密度的離群點檢測算法LOF[4],提出基于密度的數據點離群度計算方法,主要定義如下:

定義1[4]ε-鄰域和數據點p的k-距離。p為數據集D中數據點,ε為距離參數值,k為自然數,d為歐氏距離函數:

1)p的ε-鄰域Nε(p)={x∈D|d(p,x)≤ε}。

2)數據點p的k-距離k-dist(p)定義為p與距其第k近的數據點的距離,p的k-鄰域簡寫為Nk(p),Nk(p)={x∈D|d(p,x)≤k-dist(p)}。

ε-鄰域用于確定數據點的密度特征比較范圍,即每個數據點的密度特征與其ε-鄰域內的數據點比較。

定義2[4]p的核心距離。p為數據集D中數據點,ε為距離參數值,MinPts為給定自然數,p的核心距離定義如下：

core-distanceε,MinPts(p)=

即當p的ε-鄰域內數據點數目大于MinPts時,p的核心距離定義為p的MinPts-距離。

定義3[4]p關于o的可達距離。p與o為D中數據點,p∈Nε(o),則p關于o的可達距離定義為:

reachability-distanceε,MinPts(p,o)=

定義4[4]p的局部可達密度。p為D中數據點,參數定義如上,p的局部可達密度定義為:

lrdMinPts(p)=

p的局部可達密度表征了p的局部密度,值越大,p所代表的局部區域越稠密。

定義5[4]p的離群因子。p為D中數據點,p的離群因子定義如下:

p的離群因子定義為p的k-鄰域內數據點與p點局部可達密度的平均比值,數據點的離群因子值越高,說明p點與其鄰域內數據點密度特征差異越顯著,其成為離群點的可能性也就越大。

分析圖1中p、q、r的數據分布特征發現,由于q較p更靠近聚類C1,因而q的局部密度高于p,而p與q的k近鄰點集均由分布均勻的C1中數據點構成,得出p的離群因子高于q的錯誤判斷;對r與p也可進行類似分析,發現LOF方法對數據分布異常情況下數據點的離群因子確實存在錯判的可能。

1.2 INFLO算法

在LOF方法的基礎上,文獻[11]提出了新的判定數據點離群因子的方法,相關定義如下:

定義6[11]p的反向k近鄰。p的反向k近鄰定義如下:RNNk(p)={q|q∈D,p∈NNk(q)}。

定義7[11]p的局部密度。den(p)=1/k-dist(p)。

定義8[11]p的離群影響因子INFLOk(p)。p的離群影響因子INFLOk(p)定義如下:

其中：

ISk(p)=NNk(p)∪RNNk(p)

相對于LOF算法,INFLO算法既考慮數據點的k近鄰,又兼顧數據點的反向k近鄰,可以更好地表征數據點所在區域的密度特征。

重新分析圖2所示數據分布異常的情況可以發現,考慮了反向k近鄰后,p的離群因子明顯小于q與r的離群因子,符合數據實際分布情況。

2 離群點檢測算法LDBO

2.1 算法思想

盡管INFLO算法通過引入反向k近鄰有效地解決了數據分布異常情況下的離群點檢測問題。但對每個數據點計算反向k近鄰使得算法的時間消耗激增。考慮現實世界,分布異常的數據通常只占數據集的一小部分,大多數數據點都屬于正常模式(非離群點),大量數據點無需反向k近鄰計算即可進行離群判別。

因此,考慮基于INFLO算法,從數據點密度特征角度研究數據點與其鄰域內數據的離群關系,設計判斷策略,在不影響INFLO算法判段正確性的前提下,盡可能減少需進行反向k近鄰分析的數據點規模,提升離群分析效率。

2.2 局部密度聚類與離群判定

聚類分析和離群點檢測有著密切聯系, LOF算法和INFLO算法均借助密度聚類的重要概念k近鄰距離來衡量數據集中各個數據點是否為離群點。而實際數據集中離群點所占的比例很小,占數據集主體的各個聚簇內的大多數數據點都不屬于離群點,但是為了避免離群點檢測中“拒真”(false negative)現象的出現(即漏判聚簇內部可能存在的離群點),LOF算法和INFLO算法都要對各個聚簇內部的數據點進行逐一判斷,嚴重影響了基于密度的離群點檢測算法效率。

為了解決這一問題,引入下述定義:

定義9 核心影響點集(Kernel Infection Set, KIS)。p為數據集D中數據點,p的核心影響點集稱KISk(p)={o|o∈NNk(p)∧p∈NNk(o)}。

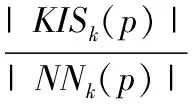
由定義可知,若p為強k近鄰點,意味著p的k近鄰內至少占比不小于μ的數據點的k近鄰也包含p,即p的k近鄰內有較大比例μ的數據點周圍區域的密度分布趨于p周圍數據密度分布。滿足μgt;0,則圖1中的p、q、r點不可能為強k近鄰點。

定義11 局部核心點。若p∈D,且

稱p為局部核心點。p的k近鄰距離不大于其k近鄰內數據點k近鄰距離的均值,說明p的k近鄰內數據點總體上向p收斂,p的局部密度高于其k近鄰數據點的平均密度。

性質1 若p為局部核心點,p一定不是離群點。

證明 從局部密度聚類角度考慮,p的k近鄰距離不大于其k近鄰內數據點k近鄰距離的均值,說明p鄰域內數據點總體上向p聚集,p對應聚簇的核心點,以p為起點遍歷其密度相連數據點,可以生成一個聚簇;同時,p鄰域內不可能出現類似圖1的數據分布異常現象,無需考慮其反向k近鄰數據點的形象,根據LOF算法離群因子定義和局部核心點的定義易得p的離群因子小于1。從這兩方面分析,p都不符合離群點的特征,p不是離群點。

證畢。

性質2p為局部核心點,且p為強k近鄰點,若q∈KISk(p),且k-dist(q)≤k-dist(p),則q也是局部核心點。

證明 由性質1,p為局部核心點不是離群點,有如下關系:

(1)

數據點q的k近鄰內點的k近鄰距離均值為:

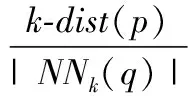
由式(1)有:

avg(q)≥

由于k-dist(q)≤k-dist(p),有

對分子部分的兩個求和表達式進行分析,對o∈KISk(p),即同時屬于點q和點p的k近鄰點集的數據點。分析可知,這類數據點的數目很少,因為在q的k近鄰內,p不可能與q很靠近,這些點又位于q的k近鄰內,將導致p的k近鄰點集中較多的數據點位于以p、q連線為直徑方向的球狀區域(如圖3中r1和r2)。而題設中有p為強k近鄰點,故而可知p的k近鄰內數據點總體上密度分布與p相近;且k-dist(p)小于其k近鄰內數據點k近鄰距離均值,若p的k近鄰點集內較多數據點位于q的k近鄰點集,將很難同時滿足這兩點。有進一步分析可知,即便p的k近鄰內有極少的數據點o在q的k近鄰內,k-dist(o)≤dist(o,q)+k-dist(q)。例如圖示k=5時,有2個數據點屬于KISk(p),同時p為強k近鄰點,則p顯然不滿足局部核心點的條件。

圖3 數據分布示意圖

對于滿足o?NNk(p)∧o∈NNk(q)條件的這類數據點一定存在,否則p的k近鄰點集中的部分數據點和p點將構成q的k近鄰點集,這將導致p為局部核心點和p為強k近鄰點兩個條件的無法同時滿足;并且這類數據點與可能存在的o∈NNk(p)∧o∈NNk(q)的數據點同屬q的k近鄰,其k近鄰距離相近。

通過上述分析可知,

ηgt;0

q為局部核心點。

證畢。

引入局部離群度定義如下:

定義12 局部離群因子(LOCal Outlierness, LOCO)。若p∈D,0lt;μ≤1,p的局部離群因子為LOCOk(p)。

通過引入強k近鄰點和弱k近鄰點,若p為強k近鄰點,由強近鄰點定義知,此時p的鄰域內不可能出現類似圖1的數據分布異常情況,故而無需考慮p的反向k近鄰內點對p離群判斷的影響;若p為弱k近鄰點,則p的鄰域內可能存在數據分布異常現象,此時對p的離群性判定需進一步考慮其反向k近鄰的影響。

2.3 數據點離群判斷策略

根據定義10,將數據點劃分成兩類——強k近鄰點集和弱k近鄰點集。若p為強k近鄰點,說明p的k近鄰內一定數量的數據與p的數據分布相近,不存在圖1所示異常的情況;否則,說明p的k近鄰內數據點可能存在分布異常的情況,容易驗證圖1中的p、q、r顯然屬于弱k近鄰點。對這兩類數據點,分別采用不同的策略進行處理。

1)強k近鄰點的離群判別。

若p為強k近鄰點,說明其k近鄰內超過100×μ%(0.5≤μ≤1)的數據分布與p相近,不存在數據分布異常情況,對p的離群判斷,不需要考慮其反向k近鄰的影響。

進一步判斷p是否為局部核心點,若p不是局部核心點,則LOCOk(p)gt;1,可能為離群點,若LOCOk(p)gt;t(假設t為所設離群因子閾值),則p為離群點;若p為局部核心點,由性質1得p不是離群點,進一步分析其k近鄰內數據點。

若p為局部核心點,可以將p的k近鄰內數據點分為三類:

①o∈NNk(p)-KISk(p)。

這一類數據點的k近鄰不包含p,對應局部密度高于p的區域,從密度聚類角度分析,與p可能屬于同一聚簇也可能屬于不同聚簇,其離群性與p沒有直接關系,盡管其局部密度高于非離群點p的局部密度,但并不意味這類數據點一定都不是離群點,仍需進一步分析其局部k近鄰內數據分布情況以判斷這類數據點是否為離群點。

②o∈KISk(p),且k-dist(o)≤k-dist(p)。

由性質1和性質2,o不是離群點。

③o∈KISk(p),且k-dist(o)gt;k-dist(p)。

這類數據點同樣屬于p的強影響點集,與情況②的區別是這些點可能不是局部核心點,因而有成為離群點的可能,必須進一步分析其k近鄰數據點的分布情況,以確定是否為離群點。從而,當判斷出強k近鄰點p非離群點的同時,可以根據性質2將p的k近鄰點集中k近鄰距離小于等于p的點標注為非離群點。

2)弱k近鄰點的離群判別。

這樣,通過強k近鄰點與弱k近鄰點的定義,可以將數據集中數據點劃分為無需考慮反向k近鄰直接進行離群判斷和需要考慮反向k近鄰進行離群判斷兩類。數據集中的絕大多數數據點屬于前者,從而無需對每個數據點分析計算其反向k近鄰數據點的影響,避免了頻繁分析計算反向k近鄰對算法效率的影響;另一方面,對占數據集比重較大的強k近鄰點,通過性質2,可以對其k近鄰內的部分待判定數據點進行預判斷,減少待判定數據點的數量,提高離群點檢測算法的效率。

2.4 LDBO算法

算法 LDBO。

輸入 維數據集D、k; 離群因子閾值t。

輸出 數據集D的離群點集合Outlier。

Initialization;

For eachxinD{

If (xnot be marked as outlier or non-outlier){

GenNNK(x,D,k);

L=NNk(x);

For (i=1;i≤|L|;i++){

Generate(L[i],D,k);

Ifx∈NNk(L[i]){insertL[i] intoKISk(x)}

}

If (|KISk(x)|/NNk(x)≥μ){

//x為強k近鄰點

GenMKDist(L,D,k);

//計算x的鄰域點k-Dist均值

If (xis local core){

xis marked as non-outlier;

For (i=1;i≤|L|;i++){

If (k-Dist(L[i])≤k-Dist(x))

xis marked as non-outlier;

}

}

else

{ If (LOCOk(x)≤t)xis marked as non-outlier;

Else {xis marked an outlier;}

}

}

else

//x為弱k近鄰點

{ generateRNNk(x);

If (LOCOk(x)gt;t){xis marked an outlier;}

Else{xis marked as non-outlier;}

}

}

}

3 實驗分析

本章對所提出的LDBO算法進行性能測試。考慮LDBO算法主要基于INFLO算法[11]進行改進,在保持其離群檢測效果的同時提升檢測效率;如文獻[12]指出,INFLO算法[11]至今仍然屬于基于局部密度的離群檢測算法中效果最好的算法之一。因此,考慮只對LDBO算法與LOF算法、INFLO算法進行實驗分析。

實驗環境配置如下:Intel 1.8 GHz/512 MB,Windows 2000 Server,所用代碼均用VC++ 6.0實現。實驗所使用的數據共兩種：第一種來源于網絡入侵檢測數據集 KDD-CUP 99,該數據集中的數據對象分為五大類,包括正常的連接、各種入侵和攻擊等。為了進行實驗,分別選取1 000條記錄和10 000條記錄的兩個數據集(分別稱為KDD-CUP-1000和KDD-CUP-10000),并對數據進行適當修改,使得攻擊(即離群點)占數據集的3%,對非數值屬性維進行數值化處理。第二種是仿真數據集(Synthetic DataSet),包括2 200條數據記錄,維度為2。精度采用以下量度對算法進行評價:

檢測出的離群點總數指算法在數據集上運行后，判定為離群點的數據點數目;判斷正確的離群點數目指算法判定為離群點的數據點中真實離群點的數目。

圖4 不同算法的精度對比

圖5 不同算法的執行時間對比

圖4～5對應k=5,μ=0.5,t=1.2時,LOF算法、INFLO算法和LDBO算法在兩類實驗數據集上的運行情況。實驗結果表明,LDBO算法與INFLO算法對兩類數據集的離群點檢測精度相似,而基于LOF的離群點檢測算法檢測精度相對較低,特別是對仿真數據集,其離群點檢測精度遠低于LDBO算法和INFLO算法;由圖5可知,LDBO算法效率明顯優于另兩種算法,這符合第2章理論分析。LDBO算法通過定義強k近鄰點和弱k近鄰點對數據點進行區分處理,有效地避免了INFLO算法對所有數據點進行反向k近鄰計算分析的不足;進一步,通過性質2,對待檢測數據點進行預判斷,從而在保證檢測精度的前提下,有效地提高了占數據集較大比重的聚簇內數據點的離群點檢測效率。仿真測試數據集分布情況如圖6(a)所示，數據集包含兩個大的聚簇,中間區域存在類似圖1的數據分布異常情況。圖6(b)對應LDBO算法在仿真數據集上運行時,利用性質2進行預判斷后,實際需要分析離群因子判斷是否為離群點的數據點,與圖6(a)對比發現兩個聚簇內部相當部分的數據點可以根據性質2進行預判斷,無需作進一步的分析處理。

圖6 測試數據集與LDBO算法實際處理數據對比

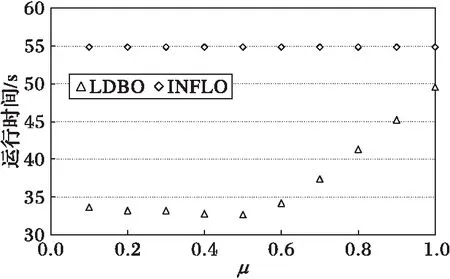
圖7 不同μ值算法執行時間對比

圖8 不同μ值算法的精度比較

進一步分析強k近鄰點和弱k近鄰點參數μ對算法性能的影響,采用仿真數據集,μ∈[0.1,1],k=5,t=1.2,對算法LDBO和基于INFLO的算法進行實驗,實驗結果如圖7～8所示。LDBO算法中,參數μ設置將影響對強近鄰點和弱近鄰點的判定,例如,μ值設置得比較低,則數據集中大部分數據點都將被判定為強k近鄰點,但這并不影響對數據集中數據點離群判定的準確性,只要μ的取值不為0,都可以有效避免圖1所示數據分布極端情況對離群點判定的影響,即使某個k近鄰內數據點分布稀疏，甚至離群點的數據點被判作強k近鄰點,按照LDBO算法思想,仍需進一步分析其是否為局部核心點以確定其離群與否, 圖8驗證了μ的取值與算法精度無關這一點。而當μ設置得很高時,則成為強k近鄰點的數據點規模越來越小,則LDBO算法對數據點進行離群預判定的作用發揮得就較少,大多數數據點都被當作弱k近鄰點需要分析其反向k近鄰以判定其離群性。由圖7可以清楚地發現這一現象,當μ大于0.6后,隨著μ的增加,LDBO算法與基于INFLO算法的時間消耗差漸漸減小。

4 結語

本文研究了基于局部密度的離群點的檢測問題,提出了LDBO算法。算法通過引入強k近鄰點和弱k近鄰點有效地解決了存在異常數據分布的數據集離群點檢測問題,將需要借助反向k近鄰點分析以判斷離群性的數據點限定在較小范圍內,進一步提出相關性質,實現對數據集中非離群點的預判定,有效提高了基于密度離群點檢測算法的效率和對數據集的適應性。

References)

[1] HAWKINS D. Identification of Outliers[M]. London: Chapman and Hall, 1980: 1-45.

[2] JOHNSON T, KWOK I, NG R. Fast computation of 2-dimensional depth contours[C]// KDD 1998: Proceedings of the Fourth International Conference on Knowledge Discovery and Data Mining. Menlo Park: AAAI Press, 1998: 224-228.

[3] KNORR E M, NG R T. Algorithms for mining distance-based outliers in large datasets[C]// VLDB 1998: Proceedings of the 24rd International Conference on Very Large Data Bases. San Francisco: Morgan Kaufmann Publishers, 1998: 392-403.

[4] BREUNIG M M, KRIEGEL H-P, NG R T, et al. LOF: identifying density-based local outliers[J]. ACM SIGMOD Record, 2000, 29(2): 93-104.

[5] PAPADIMITRIOU S, KITAGAWA H, GIBBONS P B. LOCI: fast outlier detection using the local correlation integral[C]// Proceedings of the 19th International Conference on Data Engineering. Piscataway, NJ: IEEE, 2004: 315-326.

[6] AGGARWAL C, YU P. Outlier detection for high dimensional data[J]. ACM SIGMOD Record, 2001, 30(2) : 37-46.

[7] 倪巍偉, 陳 耿, 陸介平, 等. 基于局部信息熵的加權子空間離群點檢測算法[J]. 計算機研究與發展, 2008, 45(7): 1189-1194. (NI W W, CHEN G, LU J P, et al. Local entropy based weighted subspace outlier mining algorithm[J]. Journal of Computer Research and Development, 2008, 45(7): 1189-1194.)

[8] 劉露, 左萬利, 彭濤.異質網中基于張量表示的動態離群點檢測方法[J]. 計算機研究與發展, 2016, 53(8): 1729-1739. (LIU L, ZUO W L, PENG T. Tensor representation based dynamic outlier detection method in heterogeneous network[J]. Journal of Computer Research and Development, 2016, 53(8): 1729-1739.)

[9] 黃添強, 余養強, 郭躬德, 等.半監督的移動對象離群軌跡檢測算法[J]. 計算機研究與發展, 2011, 48(11): 2074-2082. (HUANG T Q, YU Y Q, GUO G D, et al. Trajectory outlier detection based on semi-supervised technology[J]. Journal of Computer Research and Development, 2011, 48(11): 2074-2082.)

[10] 胡彩平, 秦小麟. 一種基于密度的局部離群點檢測算法DLOF[J]. 計算機研究與發展, 2010, 47(12): 2110-2116. (HU C P, QIN X L. A density-based local outlier detecting algorithm [J]. Journal o f Computer Research and Development, 2010, 47(12): 2110-2116.)

[11] JIN W, TUNG A K H, HAN J, et al. Ranking outliers using symmetric neighborhood relationship[C]// Proceedings of the 10th Pacific-Asia Conference on Advances in Knowledge Discovery and Data Mining. Berlin: Springer, 2006: 577-593.

[12] RADOVANOVIC M, NANOPOULOS A, IVANOVIC M. Reverse nearest neighbors in unsupervised distance-based outlier detection[J]. IEEE Transactions on Knowledge amp; Data Engineering, 2014, 27(5): 1369-1382.

[13] 楊慧, 王麗婧. 基于聚類和擬合的QAR數據離群點檢測算法[J]. 計算機工程與設計, 2015, 36(1): 174-177. (YANG H, WANG L J.QAR data outlier detection algorithm based on clustering and fitting[J]. Computer Engineering and Design, 2015, 36(1): 174-177.)

Fastoutlierdetectionalgorithmbasedonlocaldensity

ZOU Yunfeng1, ZHANG Xin1, SONG Shiyuan2*, NI Weiwei2

(1.StateGrid,JiangsuElectronicPowerResearchInstitute,NanjingJiangsu210036,China;2.SchoolofComputerScienceandEngineering,SoutheastUniversity,NanjingJiangsu211189,China)

Mining outliers is to find exceptional objects that deviate from the most rest of the data set. Outlier detection based on density has attracted lots of attention, but the density-based algorithm named Local Outlier Factor (LOF) is not suitable for the data set with abnormal distribution, and the algorithm named INFLuenced Outlierness (INFLO) solves this problem by analyzing bothknearest neighbors and reverseknearest neighbors of each data point at cost of inferior efficiency. To solve this problem, a local density-based algorithm named Local Density Based Outlier detection (LDBO) was proposed, which can improve outlier detection efficiency and effectiveness simultaneously. LDBO introduced definitions of strongknearest neighbors and weakknearest neighbors to realize outlier relation analysis of those data points located nearby. Furthermore, to improve the outlier detection efficiency, prejudgement was applied to avoid unnecessary reverseknearest neighbor analysis as far as possible. Theoretical analysis and experimental results Indicate that LDBO outperforms INFLO in efficiency, and it is effective and feasible.

outlier detection; local density; strongknearest neighbors; weakknearest neighbors; ReversekNearest Neighbors (RkNN)

2017- 04- 12 ;

2017- 07- 02。

國家自然科學基金資助項目(61370077)。

鄒云峰(1977—),男,江西豐城人,高級工程師,主要研究方向:數據挖掘、電力信息系統; 張昕(1987—),男,江蘇南京人,碩士,主要研究方向:數據集成、電力信息系統; 宋世淵(1992—),男,河南平頂山人,碩士研究生,主要研究方向:數據挖掘、數據隱私保護; 倪巍偉(1979-)，男,江蘇淮陰人,教授,博士生導師,博士,主要研究方向:數據挖掘、數據隱私保護、復雜數據管理。

1001- 9081(2017)10- 2932- 06

10.11772/j.issn.1001- 9081.2017.10.2932

TP274

A

This work is partially supported by the National Natural Science Foundation of China (61370077).

ZOUYunfeng, born in 1977, senior engineer. His research interests include data mining, electronic information system.

ZHANGXin, born in 1987, M. S. His research interests include data integration, electronic information system.

SONGShiyuan, born in 1992, M. S., candidate. His research interests include data mining, data privacy protection.

NIWeiwei, born in 1979, Ph. D., professor. His research interests include data mining, data privacy protection, complex data management.