航行體垂直發射過程不確定性量化方法的探討

陳 浮,馬貴輝,權曉波,姜 帥

(1.哈爾濱工業大學能源科學與工程學院,哈爾濱150001; 2.北京宇航系統工程研究所,北京100076)

航行體垂直發射過程不確定性量化方法的探討

陳 浮1,馬貴輝1,權曉波2,姜 帥1

(1.哈爾濱工業大學能源科學與工程學院,哈爾濱150001; 2.北京宇航系統工程研究所,北京100076)

在發射平臺運動、海浪及海流、氣水介質突變、空泡潰滅等的影響下,航行體水下垂直發射呈現出干擾因素隨機性強、干擾量大、彈道參數變化劇烈等特點。在分析、辨識各種干擾因素的形成機制及組成結構的基礎上,建立了描述航行體水下發射過程不確定度的數學模型;介紹了近年來國際上較為熱門的不確定性量化研究中的數值方法和進展,主要討論了基于多項式混沌理論的不確定度量化方法;最后,探討了未來航行體水下發射過程不確定性量化研究所面臨的一些挑戰和亟待解決的問題。

垂直發射航行體;不確定性量化模型;數學方法;可靠性

0 引言

采用彈射技術發射的潛射航行體,在發射平臺運動、海浪、海流、介質突變、空泡潰滅等的影響下,其繞流流場參數及所受到的流體動力、載荷等變化劇烈,并可能導致彈道失穩、結構破壞甚至發射失敗等風險。例如,俄羅斯 “布拉瓦”導彈迄今進行了21次試驗,失敗10次,其中至少5次試驗失敗是水下彈道失控,使其出水姿態偏離預設值,導致出水后發生墜海或自毀現象[1]。目前可靠性最高的美國 “三叉戟II”D5導彈,研制早期的幾次發射失敗多是彈體尾部機械載荷過大導致的,有學者認為該問題至少在部分程度上與導彈設計時低估了彈道偏轉帶來的較大水壓載荷有關[2]。

上述資料表明,航行體彈道及出水姿態的穩定性對飛行成敗至關重要,如果彈道離散度較大或不確定性較強,就很難在出水分離點處保證航行體姿態滿足點火起控允許的參數要求,顯著降低發射的可靠性和成功率。

1 潛射航行體水下發射過程不確定性因素的辨識

如圖1所示,潛射航行體水下發射過程具有干擾量大、干擾因素隨機性強、參數變化強烈等特點,影響彈道、運動姿態的各種不確定性因素按來源可分為發射環境及條件不確定性、系統不確定性兩類。

表1給出的不確定性成因分析表明,不確定性因素具有隨機性、模糊性和未確知性等特點,其微小擾動有可能給航行體水下發射過程帶來較大影響,并由此帶來彈道穩定性差、參數散布范圍大等問題。為考察不確定性因素對航行體水下發射過程的影響,實施全尺寸、系統級的潛射發射試驗無疑是最可靠的手段。樣本理論表明,基于試驗結果推斷出不確定性相關信息 (如彈道的數學期望、方差等)的前提是試驗次數足夠多。如果再考慮到發射環境及條件的非重復性、新型號預研階段技術跨越大及信息缺乏等因素,評估不確定性所需的試驗次數將非常大。限于政治、經濟及安全等原因,系統級試驗次數一般極少。依賴這些系統級試驗次數對水下發射過程中的不確定性進行分析和預測具有較大的難度。

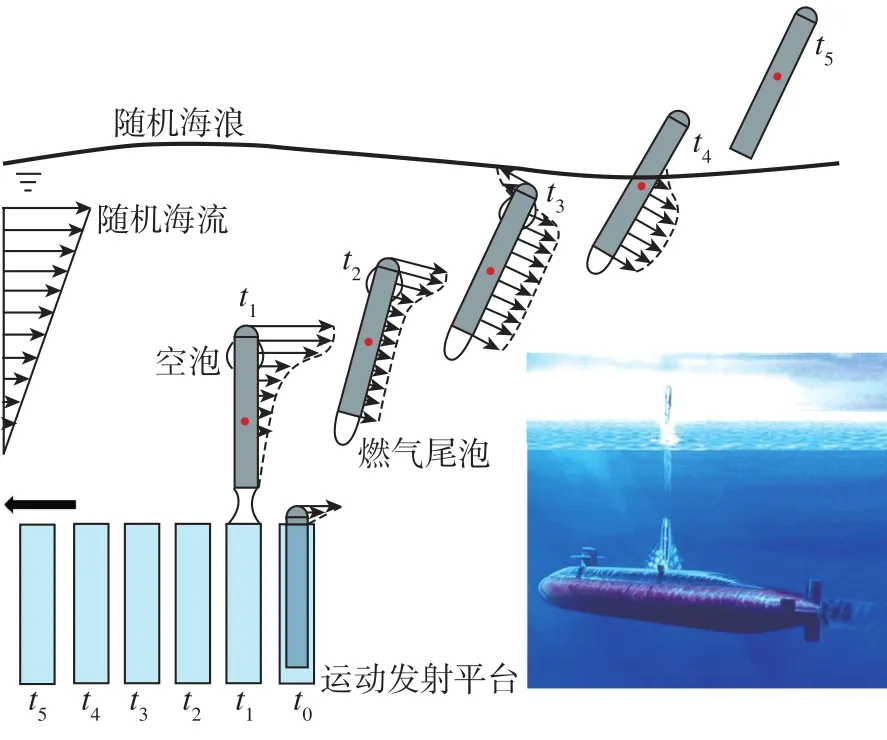
圖1 多種不確定性因素下的航行體水下發射過程Fig.1 Launch process of underwater vehicles with multiple uncertain factors impact

表1 潛射航行體水下發射過程不確定性因素辨識Tab.1 Uncertain factors of the launch process of underwater vehicles

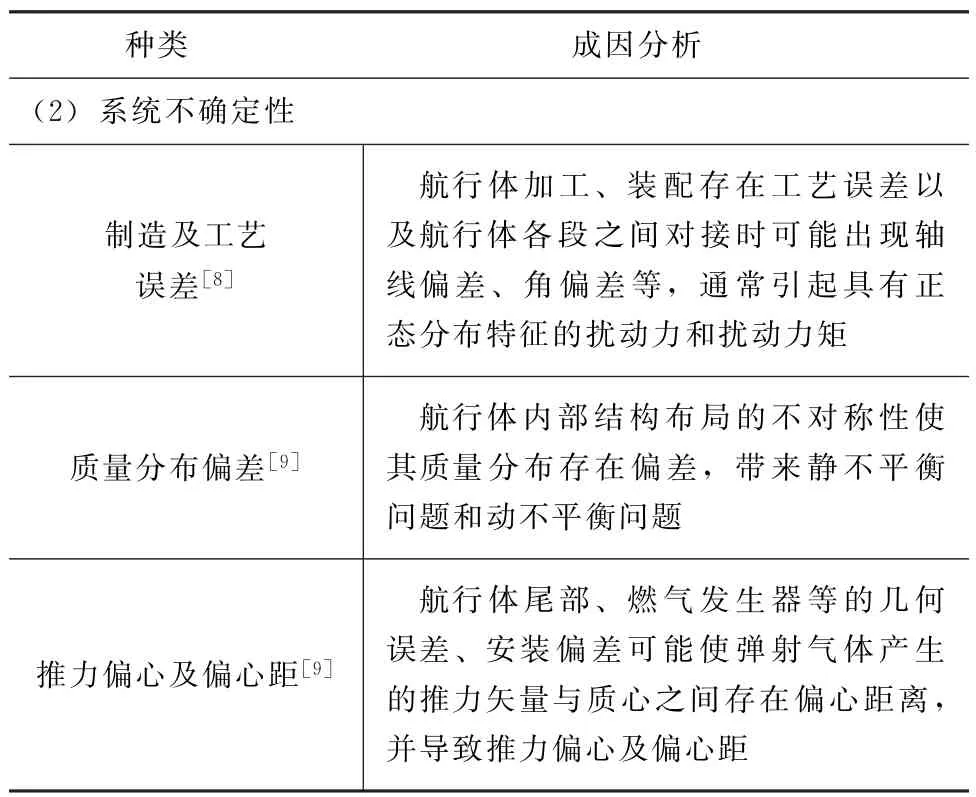
續表

于是,通過具有高可信度的數值建模與模擬(Modeling and Simulation,Mamp;S)實現航行體水下發射過程不確定性的評估和預測就成為一條有效途徑。通過Mamp;S為航行體彈道、運動姿態的穩定性及可靠性提供量化依據,需要在探索不確定度因素的組成結構及其量化理論的基礎上對不確定性因素進行量化。不確定性量化(Uncertainty Quantification,UQ)指通過辨識不確定性因素的組成結構,利用數學、統計學方法,定量描述和減少被預測系統 (航行體)行為不確定性的科學。基于UQ的Mamp;S任務的本質是通過構建系統狀態及工作環境與系統性能之間復雜而又確定的物理關系,研究并量化系統狀態及工作環境的不確定度所引起的系統性能不確定度,進而得到系統性能的不確定度度量[10-11]。

2 UQ數學方法概述

不確定性可分為物理不確定性、輸入參數不確定性、模型形式不確定性和預測不確定性等4類,或分為偶然不確定性和認知不確定性兩類[12-13]。后者是目前學術界廣泛認可的分類方式。

自20世紀末以來,UQ研究得到了眾多研究者的高度重視,成為重要的應用數學研究方向[14-15]。例如,美國能源部 (DOE)[16]及其所屬的三 大 核 武 器 試 驗 室[17-19]、 航 空 航 天 局(NASA)[20]、航空航天學會(AIAA)[21]等開展了基于UQ理論的復雜工程Mamp;S的模型驗證與確認研究工作;歐盟在航空、航天領域啟動了若干不確定性分析的研究計劃[22]。國內也開展了相應的研究工作[23-26],并取得了一些較好的成果,但仍處于起步階段。

Mamp;S中的UQ方法可分為概率法和非概率法[27]。作為概率法的一種,基于多項式混沌理論(Polynomial Chaos Expansion,PCE)的隨機譜法(Stochastic Spectral Methods,SSM)被廣泛應用于流體力學、結構力學、熱科學等領域的UQ研究中。PCE源于Wiener[28]在對布朗運動的隨機過程研究中提出的齊次混沌法。Cameron等[29]證明Hermite多項式混沌展開可收斂于具有有限2階矩的任意隨機過程。Ghanem等[30]證明了多維概率空間中的Hermite多項式可構成一族正交基,基于該多項式的混沌展開具有均方收斂特征,并首次將這種隨機變量譜展開法應用于固體力學有限元分析的UQ研究中。Ghanem[31]通過等概率法將接近正態分布的隨機變量轉換為正態分布,并利用Hermite多項式展開處理該類變量的不確定性。Xiu等[32]擴展了基于Gauss變量的Hermite多項式展開,提出了廣義多項式混沌法。其基本思想是在隨機參數空間用PCE構成無窮級數項展開式逼近隨機變量。設概率空間(Ω,F,P),令Ω為樣本空間,F為Ω上的σ代數,P:F→[0,1]為可測區間(Ω,F)的概率測度,若概率空間內描述某不確定物理過程θ∈Ω的一組隨機變量為ξ(θ)={ξ1(θ),ξ2(θ),…,ξN(θ)}T,則任一定義于該空間的隨機變量y[r,t,ξ(θ)]的多項式混沌展開式可寫為:

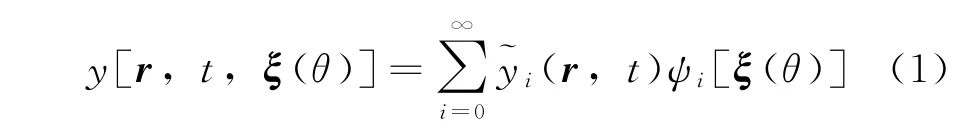
基于PCE的SSM包括隨機Galerkin法(Stochastic Galerkin Method,SGM)和隨機配置法(Stochastic Collocation Method,SCM)。其中, SCM是當今較為流行的UQ方法,它是一種非嵌入式算法,將原有數學模型視為 “黑盒子”,在隨機空間采用抽樣或其他方法選取輸入參數作為樣本,通過計算與這些特殊樣本對應的確定性問題,并將它們的解作為樣本信息來構造高精度的PCE,進而獲得輸出結果的統計特征,評估輸入參數或計算條件不確定性的傳播影響。由于SCM將需要求解的隨機問題分解為一系列特殊樣本點上的確定性問題,因而可以調用確定性問題求解器,與確定性問題的兼容性使得SCM在復雜隨機問題分析中得到廣泛應用。例如,Walters[36]在隨機變量空間采用抽樣方法選取輸入參數作為求解PCE系數的樣本。Hosder等[37]給出了SCM在隨機流動中的多個應用。

SCM的計算精度和速度極大地依賴于配置點的選取。在多維隨機空間中,基于張量積的選點策略[38]簡單直接,但會導致嚴重的 “維度災難”問題,即所需要的張量積節點個數隨著隨機空間維數、PCE階數的增長而呈指數上升,要求提供的樣本數非常巨大,考慮到對于每一個樣本都需要求解與原隨機問題同等規模的確定問題,這使得SCM的計算耗費極為高昂,甚至不可接受。為了克服維度災難問題,概率配置法(Probabilistic Collocation Method,PCM)被引入到UQ計算當中[39],它的主要思想是在高斯積分點中選取配置點,計算隨機系統的響應量,然后再映射到PCE模型上。Villadsen等[40]證明了在一維情況下以正交多項式的根作為配置點的PCM可以推廣到多維空間。Loeven等[41]發展了用Lagrange插值多項式構造隨機變量的PCM,可以在保證計算精度的情況下減少計算量,提高效率。Wang等[42]采用PCM對某壓氣機轉子進行了魯棒優化,在提高轉子氣動特性的同時降低了其對不確定性條件的敏感性。Ammaro等[43]采用Monte Carlo法和PCM分析了進口壓力變化導致的氣膜有效度及葉片壽命的不確定性變化。趙軻等[44]進行了基于PCM的翼型不確定性分析及其穩健性優化設計。在高維隨機問題中,由于多維隨機空間正交多項式的根的數量遠多于配置點數量,如何從龐大的根集中選取子集作為PCM的配置點,至今仍沒有成熟理論。近年來稀疏網格配置法(Sparse Grid Collocation Methods,SGCM)由于具有配置點個數少,有著嚴格數學理論保證計算精度等特點而得到廣泛應用[45-46]。

對于復雜系統的Mamp;S來說,輸入參數的不確定性以偶然和認知不確定性耦合在一起的混合型不確定性為主。當存在認知不確定性時,基于概率論的UQ方法不適于開展不確定性分析,需要用混合模型描述不確定性變量。例如,隨機-模糊模型、隨機-區間模型、概率-模糊-區間模型等。概率盒[27](Probability Box,P-Box)是一種概率和區間的混合模型,該模型用區間表達認知不確定性,可用于描述混合型不確定性問題,現有的概率模、區間數和證據結構等可直接轉換為P-Box的形式,在復雜系統的不確定性分析中具有良好的應用前景。Jiang等[47]用P-Box對認知不確定性進行建模,提出了統一不確定性分析模型,研究了極限狀態方程的雙重迭代模型。Zhang等[48]離散化處理P-Box變量,提出了基于區間Monte Carlo法的結構可靠性統一分析模型。Yang等[49]提出了可處理包含隨機變量和P-Box的混合可靠性分析方法。

3 航行體水下發射過程Mamp;S中的UQ模型建立

目前,航行體水下發射過程的Mamp;S方法包括:根據導彈水下受力及力矩,建立水下運動數學模型;基于CFD理論、有限體積法及動網格技術,建立水下運動耦合仿真模型。其中,后者對于航行體水下發射過程涉及的多相流問題及流體動力問題有著良好的求解能力,適于建立水下環境模型和航行體運動模型的綜合模擬系統,實現多種環境因素綜合作用與航行體運動的耦合計算,使得仿真結果更接近于實際情況。限于問題的非線性、非定常性特點,關于多相流體運動與多自由度剛體運動耦合求解的航行體水下發射過程Mamp;S方面的研究成果不但較為少見,而且幾乎都屬于確定性研究,即采用確定的模型、邊界條件和求解方法進行數值模擬及結果分析工作,并沒有考慮發射條件及環境 (如發射平臺的航速及航深、隨機浪-流參數等)不確定性、數學模型形式不確定性、數值模擬不確定性以及各種不確定性的傳播等對航行體水下彈道、出水姿態等的影響。例如,Saranjam[50]利用流動控制方程與運動方程耦合求解方法研究了航行體自由飛行時的超空泡演化過程。楊曉光等[51]利用動網格技術等航行體六自由度水下運動及出水過程進行了數值模擬,分析了發射平臺運動、波浪、自由液面等因素對航行體運動學及動力學特性的影響。鮑文春等[52]采用VOF模型及動網格技術,針對航行體排氣水下發射過程展開研究,獲得了航行體排氣水下運動過程表面壓力分布特性及氣泡形成演化規律。

由于物理過程的復雜性及認知不足,航行體水下發射過程的Mamp;S始終存在著不確定性,無法真實、完整地反映其流體動力學特征,使得彈道、運動姿態等參數的準確預測和分析變得極為困難。國內外相關文獻調研結果表明,基于UQ理論的航行體流體動力學參數的預測和評估方面的研究工作幾乎是空白,存在著許多亟待解決的問題。例如,如何構建可描述浪-流-大氣耦合效應的隨機參數分布特征的數學模型,如何通過高精度量化方法、靈敏度分析方法等緩解 “維度災難”問題,如何解決復雜系統混合型不確定性輸入參數的分析和量化問題等。

設與航行體系統狀態 (如幾何尺寸、物性參數等)有關的參數滿足表達式τ(r)=0,其中r為空間坐標;隨時空變化的發射條件及環境參數滿足式f(r,t)=0,其中t為時間;用于描述航行體水下發射過程的流體力學及運動學參數組為ξf(r,t),ξk(r,t);反映流體性質間關系的物理模型 (如本構方程、湍流模型、多相流模型等)、與航行體受力有關的經驗公式或假設寫為ηf[ξf(r,t)]=0,ηk[ξk(r,t)]=0。于是,航行體水下發射過程的多物理場耦合的非線性偏微分方程組與常微分方程組可寫為

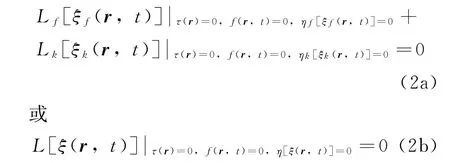
其中,L·[]為包含時空微分的算子,描述了建立在普遍物理規律之上的流體力學與運動學參數之間的函數關系。

圖2給出了航行體水下發射過程Mamp;S中不確定性因素的組成結構。輸入參數τ(r)=0、f(r,t)=0的不確定性是觀測、統計過程中產生的,稱輸入參數不確定性,一般屬于偶然和認知不確定性耦合的混合型不確定性。物理模型η[ξ(r,t)]=0及方程組L[ξ(r,t)]=0的不確定性是構造數學或力學模型過程中產生的,由于對反映物理行為的客觀規律認知不足或為降低它們的復雜度而引入簡化假設導致,是認知不確定性。輸出參數組ξ(r,t)的不確定性來源有3個:1)輸入參數及模型形式不確定性在Mamp;S過程中引起的不確定性傳播;2)應用離散數學方法求解微分方程組時引起的數值模擬不確定度,與計算域及方程的離散方法、求解算法等有關;3)上述兩類不確定性間的非線性耦合作用產生的不確定性。

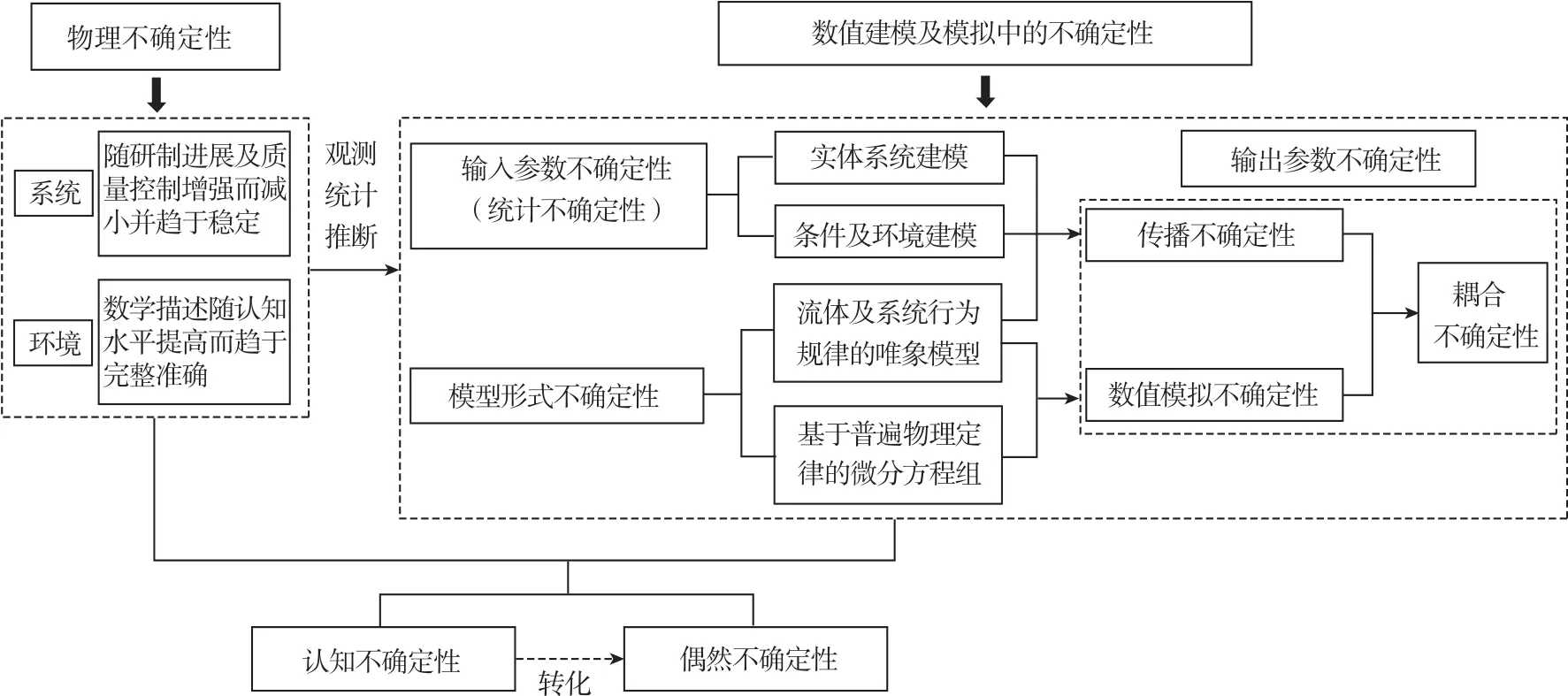
圖2 潛射航行體水下發射過程Mamp;S中的不確定性組成結構Fig.2 The composition of uncertainty within the Mamp;S of vehicle's launch process

基于上述討論,潛射航行體水下發射過程Mamp;S中的UQ模型可寫為

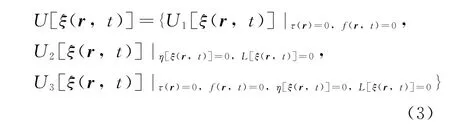
其中,U1·[]是與航行體狀態、發射條件及環境有關的不確定度,其表達式取決于統計結果、認知水平,源于對物理對象描述不精確;U2·[]是與數學或力學模型構造有關的不確定度,其函數形式取決于建模時所認知的科學理論,源于建模時沒有精確反映客觀對象的物理本質;U3·[]是數值模擬過程中產生的不確定度,其數學描述取決于數值離散方法,源于不確定性的傳播、數學求解方法沒有準確求解微分方程組以及諸多不確定性因素間的耦合效應等。

4 結論

潛射航行體水下發射過程是一個多物理場耦合的復雜物理演化過程,涉及流體力學、空氣動力學、多相流體力學、運動學等多個學科。描述這一復雜過程的數學模型是非線性流體力學方程組與運動學方程組耦合在一起的不確定性微分方程組。因此,在深入探討表征航行體水下發射過程中不確定性因素的組成結構、量化分析及傳播機制的新理論、新方法的基礎上,定量分析不確定性參數的分布特征及其數學描述對航行體流體動力學參數的影響,實現對彈道、運動姿態等的準確分析、評估及較高可信度預測,并為判斷不確定性因素誘發彈道失控模式提供數據支持,不但是航行體水下發射技術研究的一個重要方向,而且可為具有較高的可靠性、穩定性及作戰效能的新型航行體研制奠定良好基礎,極具理論價值和工程應用意義。

[1] 馬順南,徐松林.俄羅斯洲際彈道導彈及試射近況淺析[J].計算機測量與控制,2016,24(8):1-4.

[2] 王瑞臣.美國潛射彈道導彈的發展歷程[J].四川兵工學報,2009,30(11):138-140.

[3] 王彥磊,袁博,朱尚卿,等.海洋環境對潛艇活動的影響[J].艦船科學技術,2010,32(6):52-55.

[4] 張少康,苗軍,彭文輝.潛射巡航導彈水下發射非定常特性研究[J].軟件,2014,35(6):48-52.

[5] 馮振興.潛地導彈水下發射環境分析[J].導彈與航天運載技術,1996(5):43-52.

[6] 張義忠,趙世平,蔡民.美國D5導彈發射系統的技術特點分析[J].艦船科學技術,2011,33(s1): 148-151.

[7] 劉志勇,顏開,王寶壽.潛射導彈尾空泡從生成到拉斷過程的數值模擬[J].船舶力學,2005,9(1): 43-50.

[8] 寧波,陳剛,陳衛東.基于蒙特卡洛法的水下火箭攻擊彈道數學仿真研究[J].系統仿真學報,2006, 18(s2):8-12.

[9] 陳云霞,孫宇鋒,段朝陽.推力偏心影響下的飛控系統可靠性研究[J].北京航空航天大學學報,2004, 30(2):143-146.

[10] 馬智博,李海杰,殷建偉,等.可靠性數值模擬的不確定度量化[J].計算物理,2014,31(4): 424-430.

[11] 梁霄,王瑞利.混合不確定度量化方法及其在計算流體動力學迎風格式中的應用 [J].爆炸與沖擊, 2016,36(4):509-515.

[12] Rilety M E.Quantification of model-form,predictive, and parametric uncertainties in simulation-based design [D].Dayton:Wright State University,2011.

[13] Hanks T C,Cornell C A.Probabilistic seismic hazard analysis:a beginner's guide[C].Proceedings of the Fifth Symposium on Current Issues Related to Nuclear Power Plant Structures,Equipment and Piping,1994.

[14] 王瑞利,江松.多物理耦合非線性偏微分方程與數值解不確定度量化數學方法 [J].中國科學:數學, 2015,45(6):723-738.

[15] 湯濤,周濤.不確定性量化的高精度數值方法和理論[J].中國科學:數學,2015,45(7):891-928.

[16] Stern F,Wilson R V,Coleman H W,et al.Verification and validation of CFD simulations[R].IIHR Report No.4.7,Iowa Institute of Hydraulic Research, the University of Iowa,Iowa City,USA,1999.

[17] Larzelere A R.The history of the accelerated strategic computing initiative(ASCI)[R].Livermore,CA:Lawrence Livermore National Laboratory Report,2009,UCRL-TR-231286.

[18] Lawrence Livermore National Laboratory.Advanced Simulation and Computing.FY11-12 implementation plan[R].Livermore,CA:Lawrence Livermore National Laboratory Report,2010,LLNL-TR-429026.

[19] Lawrence Livermore National Laboratory.Predictive Science Academic Alliance Program-II(PSAAP-II) Verification,Validation and Uncertainty Quantification Whitepaper[R].Livermore,CA:Lawrence Livermore National Laboratory Report,2011,LLNL-MI-481471.

[20] Zang T A,Hemsch M J,Hilburger M W,et al. Needs and opportunities for uncertainty-based multidisciplinary design methods for aerospace vehicles[R]. National Aeronautics and Space Administration,Langley Research Center,NASA,2002.

[21] Oberkampf W L,Sindir M M,Conlisk A T.Guide for the verification and validation of computational fluid dynamics simulations[R].AIAA-G-077-1998,1998.

[22] Hirsch C,Dinescu C.Nodesim-CFD:a european project on non-deterministic simulation for CFD-based design methodologies[C].Computational Uncertainty in Military Vehicle Deisgn,2007,RTO-MPAVT-147.

[23] Bai W,Li L,Li Z M,et al.CFD Vamp;V and open benchmark database[J].Chinese Journal of Aeronautics,2006,19(2):160-167.

[24] 鄧小剛,宗文剛,張來平,等.計算流體力學中的驗證與確認[J].力學進展,2007,37(2):279-288.

[25] 張涵信,查俊.關于CFD驗證確認中的不確定度和真值估算[J].空氣動力學學報,2010,28(1): 39-45.

[26] Wu B S.An overview of verification and validation methodology for CFD simulation of ship hydrodynamics [J].Journal of Ship Mechanics,2011,15(6):577-591.

[27] Oberkampf W L,Roy C J.Verification and validation in scientific computing[M].Cambridge:Cambridge University Press,2010.

[28] Wiener N.The homogeneous chaos[J].American Journal of Mathematics,1938,60(4):897-936.

[29] Cameron R H,Martin W T.The orthogonal development of non-linear functionals in series of Fourier-Hermite functionals[J].Annals of Mathematics, 1947,48(2):385-392.

[30] Ghanem R G,Spanos P D.Stochastic finite elements:a spectral approach[M].Dover Publications,1991.

[31] Ghanem R.Stochastic finite elements with multiple random non-Gaussian properties[J].Journal of Engineering Mechanics,1999,125(1):26-40.

[32] Xiu D,Karniadakis G E.The Wiener-Askey polynomial chaos for stochastic differential equations[J]. SIAM Journal on Scientific Computing,2002,24 (2):619-644.

[33] Soize C,Ghanem R.Physical systems with random uncertainties:chaos representations with arbitrary probability measure[J].SIAM Journal on Scientific Computing,2004,26(2):395-410.

[34] Wan X,Karniadakis G E.Multi-element generalized polynomial chaos for arbitrary probability measures [J].SIAM Journal on Scientific Computing,2006, 28(3):901-928.

[35] Oladyshkin S,de Barros F P J,Nowak W.Global sensitivity analysis:a flexible and efficient framework with an example from stochastic hydrogeology[J]. Advances in Water Resources,2012,37:10-22.

[36] Walters R W.Towards stochastic fluid mechanics via polynomial chaos[C].Proceedings of the 41stAIAA Aerospace Sciences Meeting and Exhibit,AIAA-2003-0413,2003.

[37] Hosder S,Walters R W,Perez R.A non-intrusive polynomial chaos method for uncertainty propagation in CFD simulations[C].44thAerospace Sciences Meeting and Exhibit,2006.

[38] Babuska I,Nobile F,Tempone R.A stochastic collocation method for elliptic partial differential equations with random input data[J].SIAM Journal on Numerical Analysis,2007,45(3):1005-1034.

[39] Tatang M A,Pan W,Prinn R G,et al.An efficient method for parametric uncertainty analysis of numerical geophysical models[J].Journal of Geophysical Research:Atmospheres,1997,102(D18): 21925-21932.

[40] Villadsen J,Michelsen M L.Solution of differential equation models by polynomial approximation[M]. New Jersey,Prentice-Hall,1978.

[41] Loeven G J A,Witteveen J A S,Bijl H.Probabilistic collocation:an efficient non-intrusive approach for arbitrarily distributed parametric uncertainties[C]. Proceedings of the 45thAIAA aerospace sciences meeting,2007,6:3845-3858.

[42] Wang X,Hirsch C,Liu Z,et al.Uncertainty-based robust aerodynamic optimization of rotor blades[J].International Journal for Numerical Methods in Engineering,2013,94(2):111-127.

[43] D'Ammaro A,Montomoli F.Uncertainty quantification and film cooling[J].Computersamp;Fluids, 2013,71:320-326.

[44] 趙柯,高正紅,黃江濤,等.基于PCE方法的翼型小確定分析及穩健設計[J].力學學報,2014,46 (1):10-19.

[45] Song X,Zhan C,Kong F,et al.Advances in the study of uncertainty quantification of large-scale hydrological modeling system[J].Journal of Geographical Sciences,2011,21(5):801-819.

[46] Narayan A,Gittelson C,Xiu D.A stochastic colloca-tion algorithm with multifidelity models[J].SIAM Journal on Scientific Computing,2014,36(2): 495-521.

[47] Jiang C,Han X,Li W X,et al.A hybrid reliability approach based on probability and interval for uncertain structures[J].Journal of Mechanical Design,Transaction of the ASME,2012,134(3): 310-311.

[48] Zhang H,Mullen R L,Muhanna R L.Interval Monte Carlo methods for structural reliability[J].Structural Safety,2010,32(3):183-190.

[49] Yang X,Liu Y,Zhang Y,et al.Hybrid reliability analysis with both random and probability-box variables [J].Acta Mechanica,2015,226(5):1341-1357.

[50] Saranjam B.Experimental and numerical investigation of an unsteady supercavitating moving body[J].Ocean Engineering,2013,59:9-14.

[51] 楊曉光,陳煥龍,劉華坪,等.導彈水下運動及出水過程的三維流場仿真[J].彈道學報,2010,22(1): 107-110.

[52] 鮑文春,權曉波,魏海鵬.航行體排氣水下發射流體動力數值仿真研究 [J].導彈與航天運載技術, 2014(5):14-18.

Discuss of Mathematical Methods for Uncertainty Quantification in Motion Process of Vertical Launched Underwater Vehicle

CHEN Fu1,MA Gui-Hui1,QUAN Xiao-Bo2,JIANG Shuai1
(1.School of Energy Science and Engineering,Harbin Institute of Technology,Harbin 150001,China; 2.Beijing Institute of Astronautical Systems Engineering,Beijing 100076,China)

Considering the influential factors,such as the mobile launching platform,ocean currents and waves,the variation of the parameters of water and air,cavity collapse,the interfering factors are random and significant,and the parameters of the ballistic trajectory change so much when a vehicle is launched under water.Firstly in this paper,based on the analysis and identification of the mechanism as well as the composition structure of the various interfering factors,the uncertainty quantification model of motion process of the underwater vehicle is established.Then, the recent progress on the mathematical methods for uncertainty quantification is reviewed briefly, the emphasis will be a method based on generalized polynomial chaos.Also,some challenging and open problems for the uncertainty quantification research in motion process of launched vehicles under water will be discussed.

Vehicles under water;Uncertainty quantification model;Mathematical methods;Reliability

O352

A

2096-4080(2017)04-0065-08

2017-09-13;

2017-11-03

國家自然科學基金(51679005)

陳浮(1970-),男,博士,教授,主要研究方向為多相耦合流動仿真、不確定性量化。Email:chenfu@hit.edu.cn