基于對角遞歸神經網絡的小區用電負荷預測研究

徐建軍 杜薔楠 閆麗梅

(東北石油大學電氣信息工程學院)

基于對角遞歸神經網絡的小區用電負荷預測研究

徐建軍 杜薔楠 閆麗梅

(東北石油大學電氣信息工程學院)

為了提高小區用電負荷預測的準確度，在研究對角遞歸神經網絡的基礎上，分析比較幾種優化算法，提出基于粒子群算法的對角遞歸神經網絡預測方法。通過對小區用電負荷影響因素的分析以及對大量歷史數據進行訓練，最后經Matlab仿真分析，結果表明：該方法預測的準確度較高。

對角遞歸神經網絡 用電負荷預測 粒子群算法

負荷分析是實現當地電力規劃的前提和基礎，尤其對研究小區用電負荷的變化趨勢和特點具有重要意義。小區用電負荷預測按照預測期限可以分為即期預測(日或周)、短期預測(12～24個月)、中期預測(5～10年)和長期預測(10～30年)[1]。筆者對小區用電負荷的預測屬于短期預測。長期以來，中外學者以及相關的電力工作人員在豐富的研究與實際工作中積極探索精確度更高、效果更好的用電負荷預測方法，主要分為傳統的數學統計類預測方法和新型的人工智能預測方法。

人工神經網絡(Artificial Neural Network，ANN)是采用數學手段來模擬人類大腦或生物神經元網絡的非線性系統，包含了大量人工神經元，每個簡單的神經元通過不同的拓撲結構組合，形成的神經網絡卻十分復雜，功能也變得很強大。它通過比較多個不相關的因子來得到最佳的參數，用于分析自變量與因變量兩者的聯系，它的優勢在于能夠很好地解決非線性問題，即使在學習的過程中出現了特殊情況，增加了特殊變量，這些都不影響它的學習能力，反而能夠使得最優參數經過對比學習后得到進一步的優化和調整。所以將ANN技術運用到電力負荷預測中十分適合。它不需要假定輸入變量的相關信息，也無需依靠專家經驗，僅利用現有數據即可通過訓練抽取和逼近輸入輸出之間隱含的非線性關系[2]。

1 對角遞歸神經網絡

對角遞歸神經網絡(Diagonal Recurrent Neural Network，DRNN)是一種反饋神經網絡，它依賴神經元之間內部的反饋來描述動態行為，使神經網絡具有反饋的性能，且能生動形象地反映出系統的動態特性，不用存儲所有的輸入信息，用較少的記憶單元就可反映出非線性系統的動力學特性[3]。

1.1DRNN模型結構

DRNN神經網絡算法可表示為：

(1)

Xj(k)=f(Sj(k))

(2)

(3)

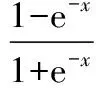
(4)

DRNN神經網絡辨識結構如圖1所示[4]。圖中k是網絡的迭代步數，DRNN為網絡辨識器，u(k)為辨識器的輸入，y(k)為被控對象實際輸出，ym(k)為DRNN的輸出結果，將y(k)和u(k)的差值作為DRNN的調整信號，則有：

逼近誤差e(k)=y(k)-ym(k)

(5)

(6)

圖1 對角遞歸神經網絡結構

1.2BP算法訓練DRNN網絡

神經網絡中應用最為常見的是BP算法。該算法的學習規則是最小均方誤差準則，學習過程由正反向傳播共同組成。正向傳播指的是信號經過一系列的分析計算，最后在輸出端得到了正確的結果，如果結果錯誤，則開始反向傳播，即將前面所得的結果和期望結果作差處理后作為反向的輸入信號，反過來從輸出端輸入。

假設一個非線性系統的數學模型為：

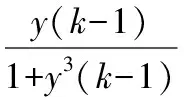
(7)

輸入信號為：

(8)

這里筆者所用到的對角神經網絡的拓撲結構為2-7-1，即兩個輸入神經元，7個中間隱含層神經元，一個輸出神經元；迭代次數為100，采樣頻率為1kHz，學習速率設為0.35，最后加入動量因子α來調整，α=0.1。

測試信號為：

u(k)=0.7sin(4πkt/25)+0.3sin(4πkt/1000)

(9)

采用BP算法訓練對角遞歸神經網絡的具體步驟為：

a. 初始化各項基本參數，提供足夠的樣本。

b. 正向傳播計算，得到該過程中各層網絡參數值。

c. 根據式(5)計算逼近誤差。

d. 根據權值調整算法調整各層網絡的權值。

e. 判斷步驟d所得的誤差精度是否合格。

f. 如若符合要求，將權值保存起來并且訓練到此結束；如果不符合要求，則返回步驟b重新開始下一輪計算。

仿真結果如圖2所示，從圖中可以看出，虛線的逼近輸出隨著迭代次數的增多，出現逐漸偏離實際輸出(實線)的現象，尤其是峰頂毛刺突出極為嚴重，總體效果一般。逼近誤差圖(圖3)表明，毛刺出現在中間的概率較大，當迭代次數接近100時，均方差幾乎收斂于0.000 1。這主要是由于訓練初期各項參數的初始值選取不當，使網絡辨識不穩定，參數的正確與否是DRNN的核心問題，初始權值的選擇會對DRNN的性能產生很大影響，所以筆者采用粒子群算法來優化對角遞歸神經網絡。

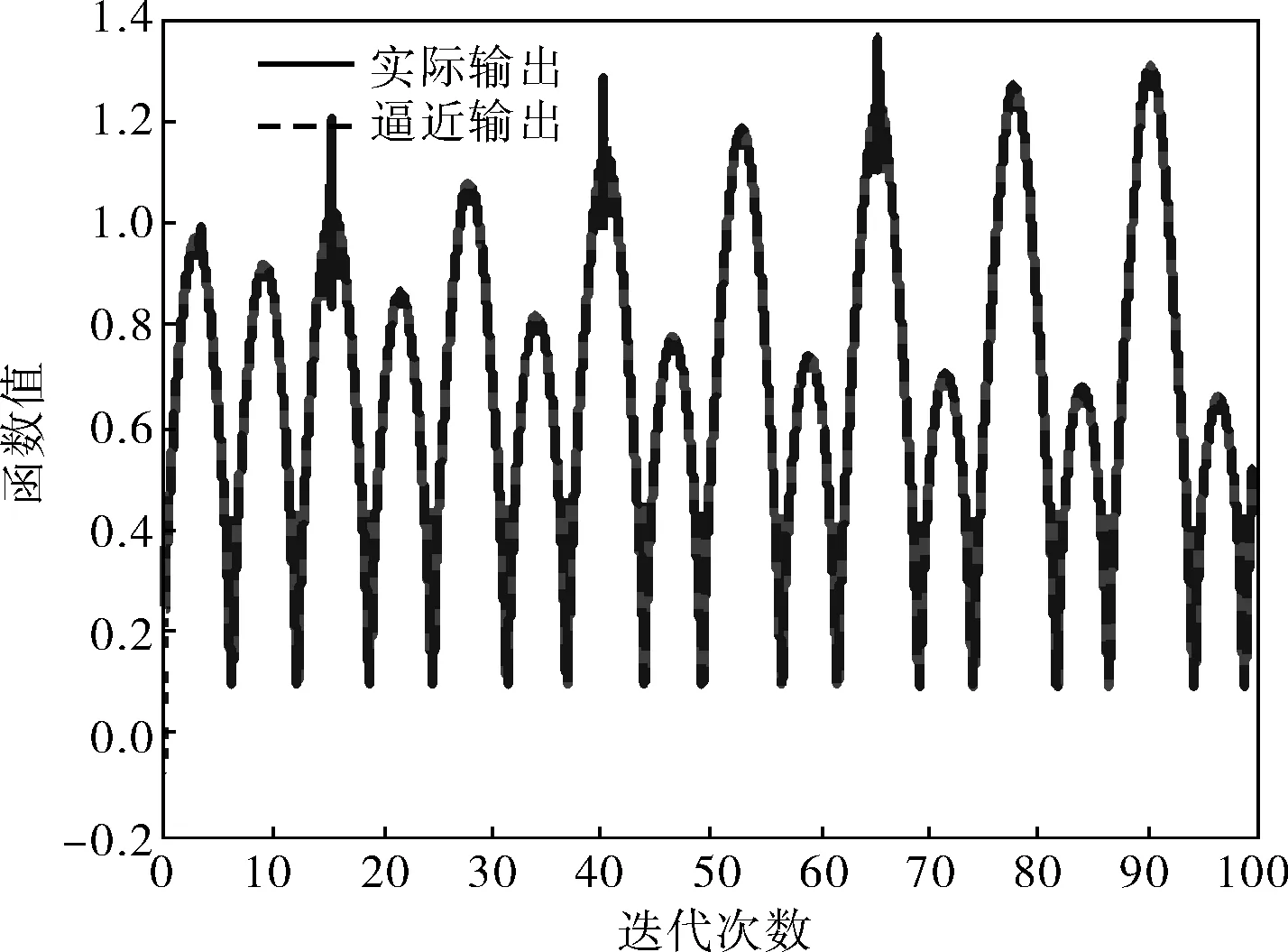
圖2 BP訓練DRNN網絡的仿真結果

圖3 BP訓練DRNN網絡的逼近誤差

2 粒子群優化算法

粒子群優化算法(Particle Swarm Optimizer，PSO)作為一種全局優化算法，它的基礎是迭代模式，這種算法通過鳥群的覓食來體現，鳥群外出集體覓食時，往往有一只頭鳥帶頭，其他的鳥跟著頭鳥，當頭鳥找到食物后，通過動物獨特的方式將信息發給鳥群，鳥群收到信息后就會朝著頭鳥的方向靠近，最終到達目的地，與頭鳥匯合。

2.1粒子群算法運算流程

根據外部變化的因素，隨時修正移動的方向和速度，通過不斷地搜索與修正，以尋找最佳的目標。每進行一次計算，粒子根據個體極值pbest尋找出最佳個體，并繼續進行重復計算迭代，個體極值尋找出全體極值gbest，此時找到目標，完成迭代過程，具體計算迭代公式如下：

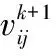
(10)

(11)

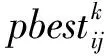
a. 粒子群初始化。任意產生的m維粒子(x1,x2,…,xm)作為最初的起始種群X(t)；各粒子初始速度定義為以(vi1,vi2,…,vim)構成的速度矩陣V(t)。

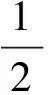
c. 調整慣性權重ω。將每一個粒子適應值和上一步的最佳個體值作出對比，若是當前粒子的適應值更好，則用當前粒子適應值代替個體最優值pbest并修改ω；同時，將該粒子的適應值和全體最優值進行比較，如果前者更好，也替換全體最優值并修改ω。

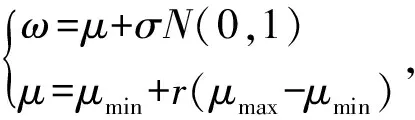
e. 停止條件。當粒子適應度達到預先要求的精度或者迭代結束時，停止迭代，反之跳轉到步驟b繼續迭代。

2.2粒子群算法尋優性能測試

尋優算法的尋優能力、性能是衡量這個算法是否可行的關鍵標準。首先針對常用的優化算法進行分析比較，這里選取遺傳算法(GA)和蟻群算法(ACO)與粒子群算法進行尋優性能測試對比。通常的方法是選取測試函數來進行測試，筆者選擇rosenbrock函數：

(12)

|xi|≤30 min(f(x))=0

迭代次數設為1 000，粒子每一維數的最大值為30，最小值為-30，學習因子c1、c2為2，慣性權重ω為0.5。仿真測試后得出的對比結果如圖4所示。

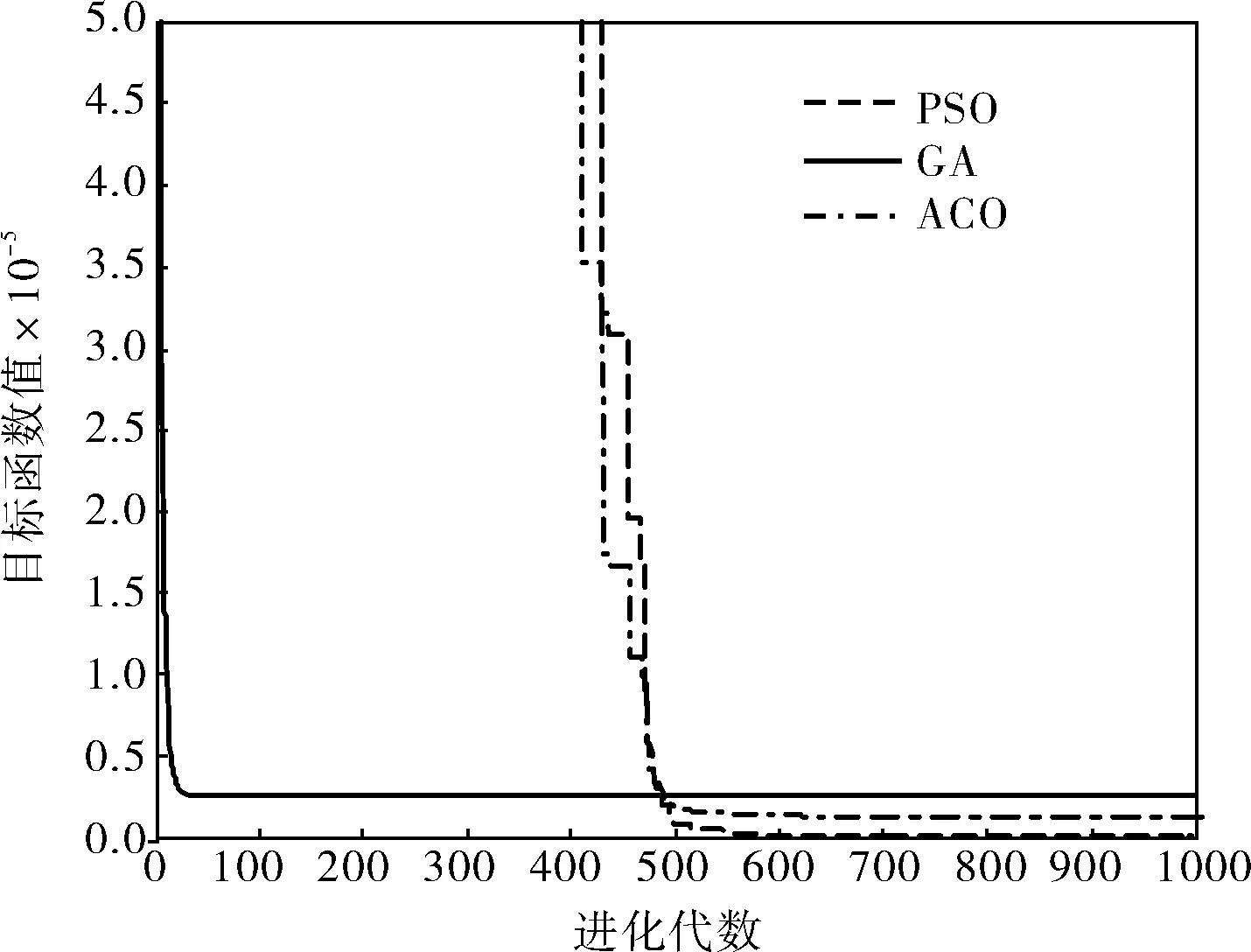
圖4 rosenbrock測試函數性能對比

仿真結果顯示對于rosenbrock函數,PSO尋優的最優目標值為5 607.4，GA尋優的結果為25 700.0，同時ACO的結果為10 832.5。從各方面來看仍然是PSO全面占優。

從上述測試函數的仿真對比來看，PSO在尋優精度和全局尋優能力上都是完全領先GA和ACO的，并且不會陷入局部最優。因此筆者采用PSO優化DRNN是完全科學可取的。

3 基于PSO-DRNN網絡的模型在小區用電負荷預測中的應用

前文已經確立了基于粒子群算法的對角遞歸神經網絡的預測方法，在進行預測前，要先考慮各種不確定因素對用電負荷的影響，分析每個因素的相關性特點以及對用電負荷影響所占的權重比例，為后面更精確地進行負荷預測奠定基礎。

根據分析，影響小區用電負荷的因素有許多，把影響因素歸納為以下幾個方面：人口因素、經濟收入因素、季節因素、節假日因素、電器因素和電價因素，這些因素對小區用電負荷都會產生或多或少的影響。筆者將這6個因素作為影響小區用電量的因素數據，與所采集的歷史數據一起進行訓練。訓練樣本采用2015年某些天的用電量數據。

圖5為模型建立的流程。圖6為粒子群優化算法的適應度曲線(c1=1.5,c2=1.7,種群數量為20)。從曲線中可以發現，適應度曲線在全局都有不斷的收斂，說明粒子群通過不斷改變位置使得適應度更優，從而得到更優的網絡權值。

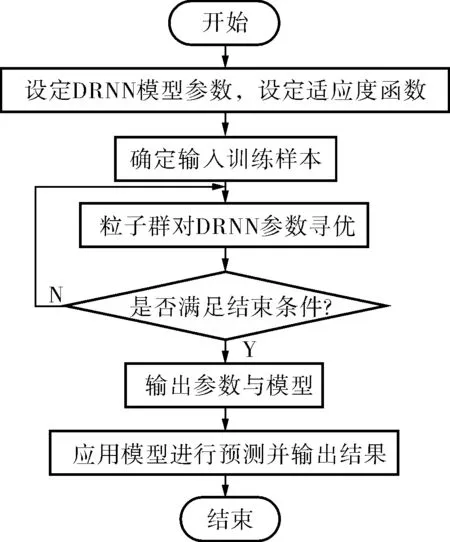
圖5 粒子群優化對角遞歸神經網絡建模流程

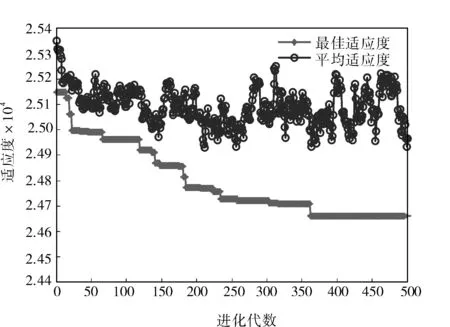
圖6 粒子群優化對角遞歸神經網絡適應度曲線

將2016年度的數據輸入到對角神經網絡模型中預測該小區每個月份的用電量，預測效果如圖7所示，反映了該小區一年中每個月的用電量變化，測試的誤差精度對于用電量的數量等級來說已經很低了，可以作為工作中評估用電量的參考。

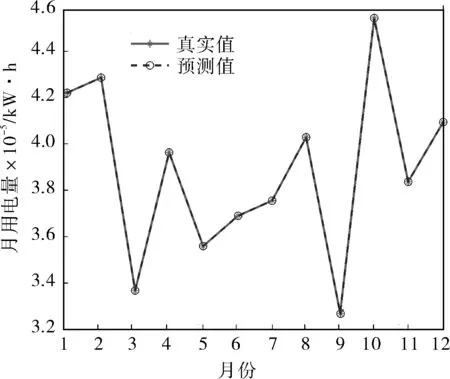
圖7 基于PSO-DRNN模型預測某小區一年用電量對比

4 結束語

筆者提出基于對角遞歸神經網絡的用電負荷預測方法，通過3種優化算法的對比，選定了全局尋優能力最好的粒子群算法來優化對角遞歸神經網絡。經實例驗證，基于PSO-DRNN的預測模型能夠通過訓練歷史數據預測未來一段時間內小區的用電量變化情況，可以認為筆者建立的PSO-DRNN模型對于小區的用電負荷預測有較好的效果。

[1] 林承就.福州市住宅小區用電負荷計算的研究[D].長沙：中南大學，2008.

[2] 王樂.基于灰色理論和神經網絡的電力系統短期負荷預測研究及其比較[D].南寧：廣西大學，2012.

[3] 龔文杰，段曉燕，張智晟.基于分布估計算法的對角遞歸神經網絡短期負荷預測模型研究[J].青島大學學報，2012，27(2)：43～47.

[4] 戴晟.基于DE算法的DRNN網絡非線性系統辨識研究[D].成都：西南交通大學，2011.

ResearchonPowerLoadForecastingofResidentialDistrictsBasedonDiagonalRecurrentNeuralNetwork

XU Jian-jun, DU Qiang-nan, YAN Li-mei

(CollegeofElectricalEngineeringandInformation,NortheastPetroleumUniversity)

In order to improve the accuracy of predicting power consumption of residential districts, having the study of diagonal recurrent neural network based to analyze and compare several optimal algorithms was implemented, including the proposal of diagonal recurrent neural network predicting method based on the particle swarm algorithm. Analyzing the factors which influencing the power consumption of residential districts and the training a large number of historical data and Matlab simulation show that, this predicting method has higher accuracy.

diagonal recurrent neural network, power consumption prediction, particle swarm optimization

黑龍江省自然科學基金項目(E2017011)。

徐建軍(1971-),教授, 從事電力理論與新技術的研究。

聯系人閆麗梅(1971-)，教授，從事電力系統安全穩定分析與控制的研究，565735794@qq.com。

TP18

A

1000-3932(2017)11-1052-05

2017-06-16，

2017-09-19)