高壓直流輸電次同步振蕩軸系扭振分析

黨存祿，嚴占想，陳 蕾

（蘭州理工大學電氣信息學院，甘肅 蘭州 730050）

高壓直流輸電次同步振蕩軸系扭振分析

黨存祿，嚴占想，陳 蕾

（蘭州理工大學電氣信息學院，甘肅 蘭州 730050）

傳統的次同步振蕩抑制方法通過阻尼濾波器阻斷機械系統和電氣系統之間的相互作用來抑制次同步振蕩，但阻尼濾波器對環境的適應性較差，設計參數要求嚴格，運行維護比較困難。因此，提出了在整流端定電流系統加入附加阻尼控制器，通過調節系統電流、增強軸系模態阻尼來抑制次同步振蕩。該控制方法實時有效，容易控制，又不會影響系統其他控制器的控制性能。通過分析發電機軸系特征值、軸系模態阻尼、次同步頻率分量的傳遞過程，研究系統控制參數、軸系模態與次同步振蕩之間的關系，設計了發電機轉速偏差與三相母線瞬時電壓聯合作為輸入信號的附加阻尼控制器，有效減小了次同步頻率變換環節的輸出誤差，提高了控制器精度。采用IEEE第一標準次同步研究模型參數，在PSCAD軟件中搭建高壓直流輸電次同步振蕩仿真模型。仿真結果表明，所設計的控制器能有效抑制系統次同步振蕩。

高壓直流輸電；次同步振蕩；特征值分析法；附加阻尼控制器；PSCAD

0 引言

高壓直流輸電（high voltage direct current transmission，HVDC）在輸電技術與經濟性方面具有諸多優勢，在輸電系統中發揮著重要的作用。HVDC技術給電力系統帶來了多方面的便利，但也會給系統的安全運行帶來新問題，如電力系統的次同步振蕩（subsynchronous oscillation，SSO）［1-3］。高壓直流輸電系統的次同步振蕩問題大多是由于HVDC控制方式引起的。當系統的次同步頻率電氣分量在不恰當控制方式的調制下，次同步電流會被控制器放大，造成發電機存在過大電流，進而引起發電機軸系過大幅值的發散擺動，造成系統發生次同步振蕩［4］。

傳統抑制次同步振蕩的方法是通過阻尼濾波器阻斷次同步電氣分量，但由于其控制參數計算復雜，在實際工程中很難實現。本文根據HVDC工作特性，建立系統次同步頻率變換、軸系扭振數學模型，在整流端定電流控制系統中加入附加阻尼控制器，并在PSCAD軟件中建立仿真模型，驗證控制器控制性能。

1 HVDC次同步振蕩分析

1.1 次同步電氣分量交直流側的傳遞關系

當整流器交直流側存在諧波作用時，不對稱的三相交流電壓 ua、ub、uc可以表示為：

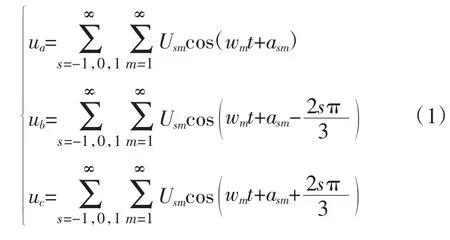
有諧波畸變的三相交流電壓經整流后的直流電壓可以表示為Udc：

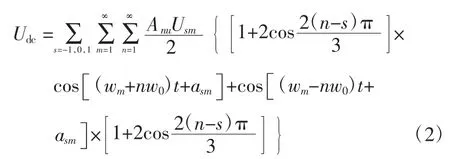
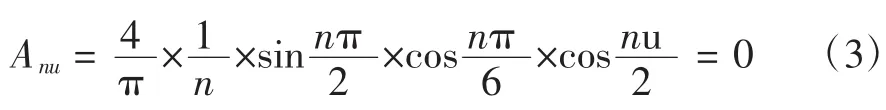
因此，當換流器在等間隔脈沖觸發控制時，零序分量不會從交流側傳遞到直流側。

對于正序分量s=1，經換流器電壓開關函數的調制作用后，直流側的電壓分量為：

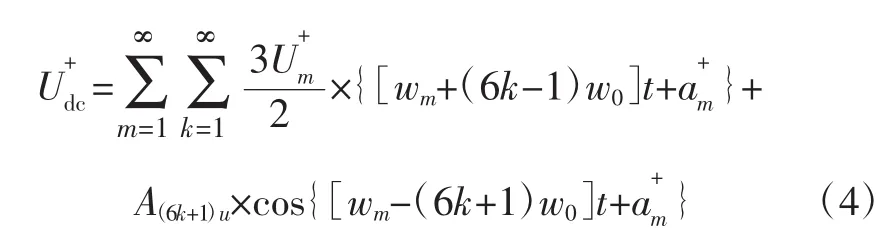
由式（4）可知，交流側頻率為wm的負序電壓諧波分量，經換流器的調制作用后，在直流側將感應出頻率為［wm+（6k-1）w0］和［wm-（6k+1）w0］的電壓分量。

直流輸電系統中，暫態分析時需考慮直流電流的紋波，直流電流可以表示成直流分量和紋波之和的形式。

式中：Id為直流電流的直流分量；Ir為紋波分量；wr為紋波分量的角頻率；βr為紋波分量的初始相角。

當紋波電流傳遞到交流側時，a相交流電流可以表示為：

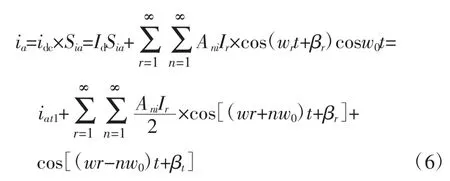
式中：iat1為換流器開關函數對直流紋波的調制作用產生的電流，其諧波頻率為 wat1=wr±（6k±1）w0。

在分析由高壓直流輸電引起的次同步振蕩時，發電機轉子上若存在擾動頻率擾動量ws，經過與發電機定子的相對運動后，將會在定子側感應出與頻率互補的次同步頻率分量（w0-ws）和超同步頻率分量（w0+ws）；發電機定子上的次同步分量又會經過輸電網絡傳輸到換流器母線，含有次同步頻率（w0-ws）的交流電壓分量經過換流器的調制作用后，直流側的電壓將產生頻率為［w0-（w0-ws）］的紋波分量，即存在頻率相對應的直流紋波電流。該紋波分量在換流器的調制作用下，也會在交流側產生頻率為（w0-ws）的次同步電流分量。

1.2 次同步電氣分量在電機上產生的電磁轉矩

當次同步頻率與定子回路中LC諧振頻率在（1-λ）處形成互補時，系統就會發生次同步諧振，線路電抗就會接近為零，此時線路總阻抗等于定子回路中的總電阻R。定子回路上產生的次同步電流可以表示為：

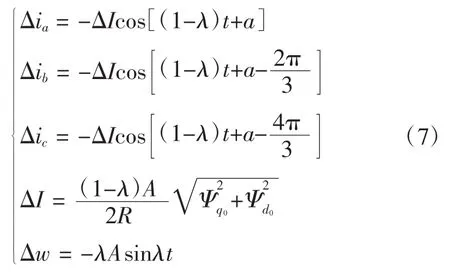
式中：A為發電機轉子角位移增量的幅值；R為發電機定子回路總電阻；Δw為角速度增量。

設次同步電流增量三相對稱，經派克變換可得發電機轉子產生的dq軸電流分量。

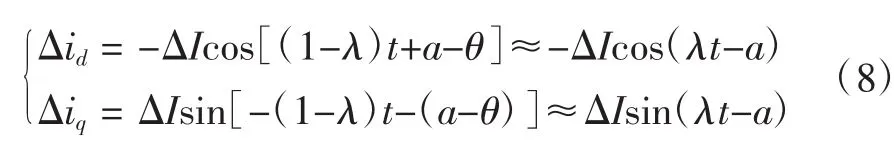
結合式（7）與式（8），可求得次同步電流增量在發電機轉子上產生的轉矩增量為：

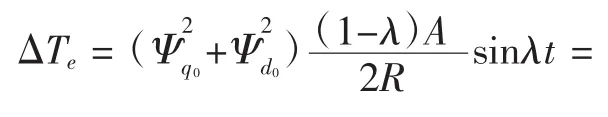
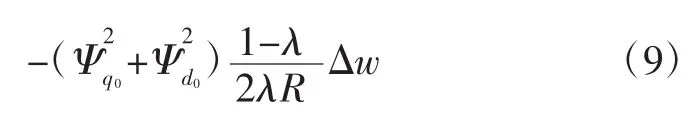
上述分析表明，當系統發生次同步振蕩時，次同步電氣分量會造成轉子上產生相應的負阻尼轉矩、軸系發生發散振蕩，破壞發電機的安全運行。

2 電力系統的阻尼特性分析

2.1 狀態變量與狀態矩陣

在小型干擾下，特征根的線性化狀態方程可以表示為：

式中：A為n×n狀態矩陣；X為n維狀態變量；I為單位矩陣；λ 為矩陣 A 的特征值，λ = λ1，λ2，λ3，…，λn。設λ1=δi+jwi，根據李雅譜諾夫第一方法，通過特征根判斷系統的穩定性［5-6］。當 wi≠ 0 時，λi= δi+jwi為一對共軛復數特征根，每一對特征根代表一種振蕩模態。其中：δi為某一模態下的阻尼，wi為某一模態的振蕩角頻率。

根據李雅譜諾夫穩定判據，若δi＜0時，表示系統穩定，即機組在該頻率模態下呈現的是正阻尼；若δi＞0時，表示系統不穩定，即機組在該頻率模態下呈現的是負阻尼。

系統的阻尼比可以表示為：

系統的阻尼比ζ代表系統振蕩衰減的速度。在一定范圍內ζ越大，振蕩衰減速度越快。對于系統的某一特征值λ1，設Li為特征值對應的列特征向量，Hi為特征值對應的行向量，則有：

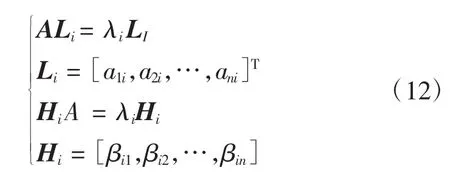
系統參與矩陣可以表示為：

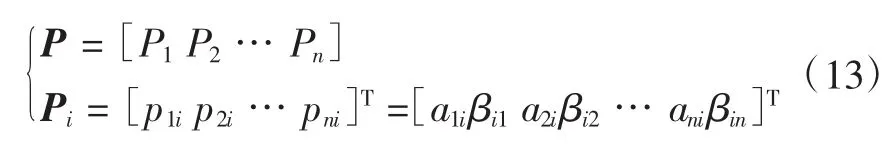
式中：aik、βki分別為特征值λi的列特征向量第 k項、行特征向量第k項；pki=akiβik為參與因子，它表示第i個模式中第k個狀態變量的相對參與度。

系統方程在運行點線性化后，可得簡化方程：

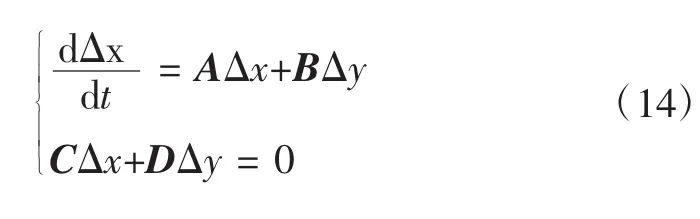
2.2 發電機軸系振蕩阻尼分析

汽輪機軸系質量塊、發電機模型參數等采用IEEE次同步振蕩研究第一標準模型參數，結合系統線性化模型、狀態方程以及HVDC單機系統運行參數，得到發電機軸系所對應的特征值及相應模態阻尼比。軸系特征根與阻尼比如表1所示。

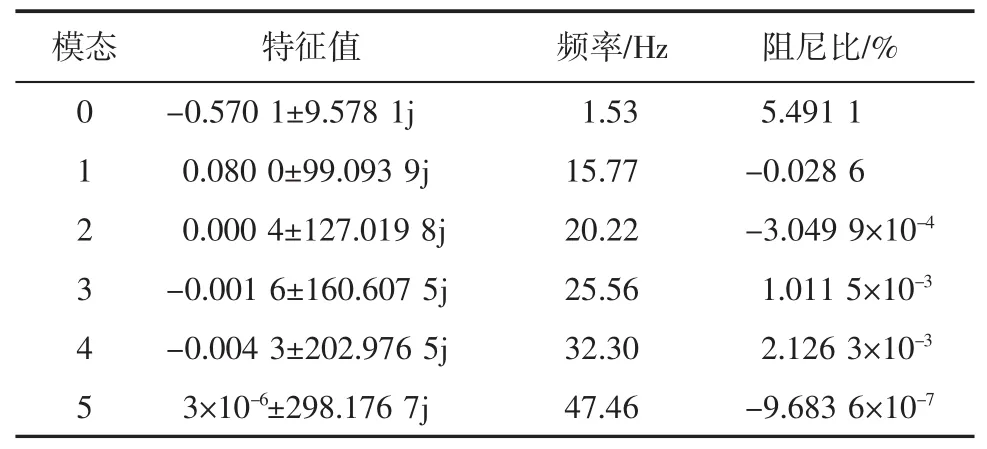
表1 軸系特征根與阻尼比Tab.1 Characteristic root and dampingratio of shafting

由表1可得以下結論。

①模態0的振蕩頻率為1.53 Hz，其特征值實部為負數，且阻尼比為5.941 1%，該模態振蕩衰減速度較快。

②模態1與模態2的特征值實部均為正數，阻尼比為負數，表示該模態下系統是發散振蕩的。其中，模態1的發散振蕩更為嚴重。

③模態3與模態4的特征值實部為負，模態阻尼比為正，說明軸系是收斂振蕩，但阻尼比數量級為10-3%，其模態振蕩衰減速度很慢。

④由模態5的特征值可以看出，雖然特征根實部為正，但其值很小，幾乎為零。次同步分量很小，故該模態為等幅振蕩模式，不易引起次同步振蕩。

模態1與模態2的特征根實部為正，容易導致軸系發散振蕩，兩者在軸段發生了相位翻轉，幅度很大。模態1與模態2，在振蕩頻率為15.77 Hz、20.22 Hz附近時，較容易發生次同步振蕩。

2.3 附加阻尼控制器SSDC的阻尼特性

附加阻尼控制器（supplementary subsynchronous damping controller，SSDC）的基本控制原理是通過在整流端電流控制器中加入一個附加的電流控制信號ISSDC，結合整流端的定電流控制系統，調節整流端電流使其維持在穩定工作狀態，為受次同步振蕩威脅的發電機組提供合適的正阻尼［7-10］。

附加阻尼控制器經過測量環節、次同步頻率變換環節、比例放大及相位補償等環節等，其輸出信號疊加到整流側定電流控制器輸入端。SSDC的傳遞函數如圖1所示。

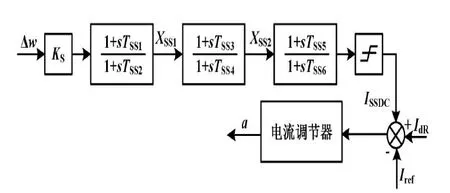
圖1 SSDC傳遞函數圖Fig.1 SSDC transfer function

圖 1 中：KS為比例系數；TSS1～TSS6為 SSDC 控制器相位補償環節的時間常數。

設 ΔXSS1、ΔXSS2、ΔISSDC為狀態變量；p為微分算子，則SSDC狀態方程可以表示為：

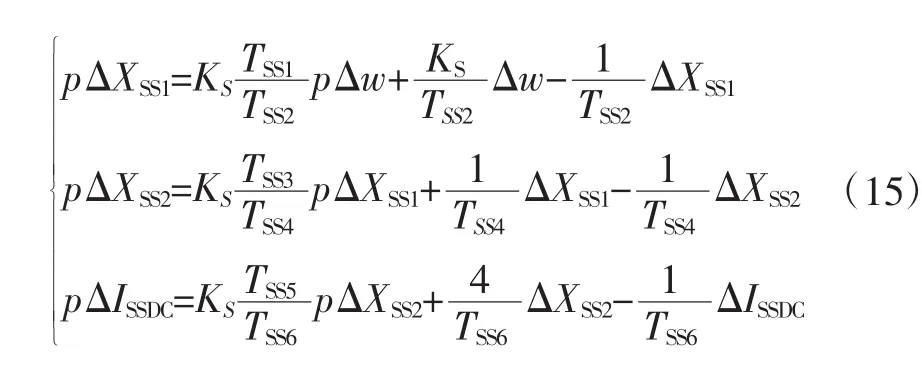
由式（15）可知，比例系數KS與輸入狀態變量ΔXSS1、ΔXSS2、ΔISSDC之間沒有關聯項。SSDC 不同放大倍數系統特征值如表2所示。由表2可知，當KS=0時，此時特征根λ3，4的實部為正，系統將會呈現負阻尼狀態，是不穩定的發散振蕩狀態；λ11，12雖然實部為正，但系數極小，出現小幅等值振蕩；其他特征根為負，此時系統為穩定狀態。

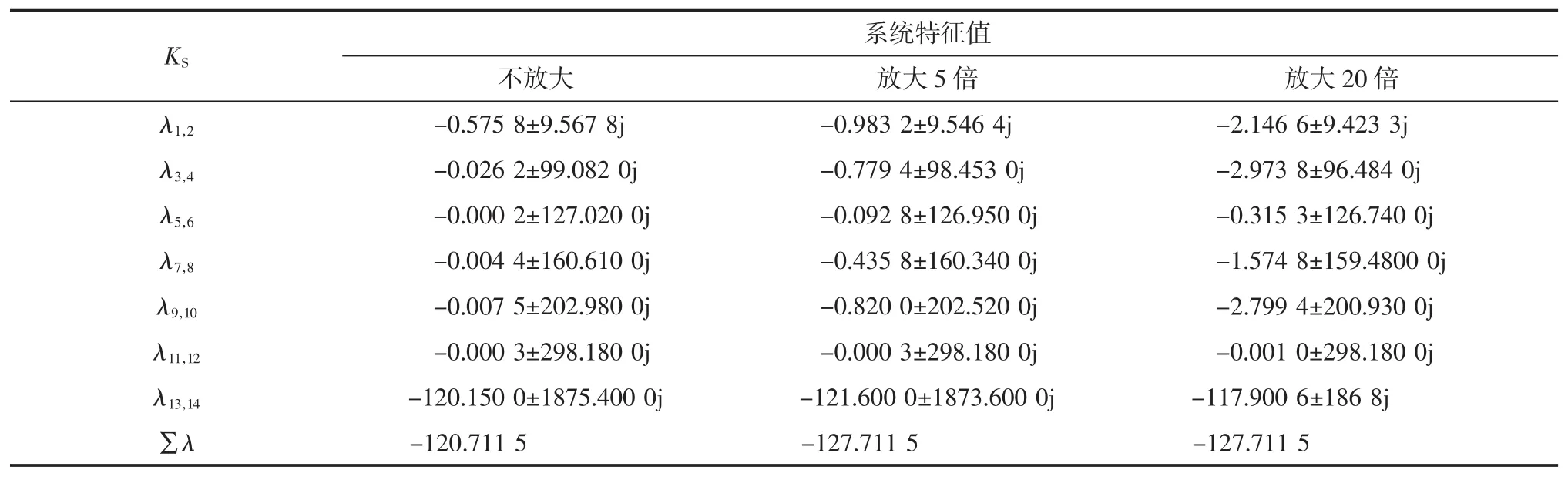
表2 SSDC不同放大倍數系統特征值Tab.2 Eigenvalue of SSDC system with different magnification

當KS=5，表示系統投入SSDC且增益系數為5，此時系統所有特征根實部全部為負，系統為穩定狀態，因此不會發生次同振蕩；λ11，12的實部由正變負，說明投入附加阻尼控制器后，系統發散模態逐漸收斂。隨著放大倍數的增大，系統許多模態阻尼均有增強，但比例系數卻不是越大越好。

表2特征值的變化情況說明SSDC在增大比例系數時，許多模態阻尼確實變強，但是某些模態的阻尼卻有所減弱。

上述數據說明，系統增強的模態阻尼是從別的模態借來的，而系統的總阻尼保持不變。由SSDC的狀態方程可知，控制器比例系數KS沒有與狀態變量相關項，不會引起系統總阻尼的變化；而系統狀態方程中的 TSS與狀態變量 ΔXSS1、ΔXSS2、ΔISSDC之間有關聯項，可能會出現在系統狀態方程的對角線上，影響總阻尼。

3 仿真分析

高壓直流輸電PSCAD模型如圖2所示。

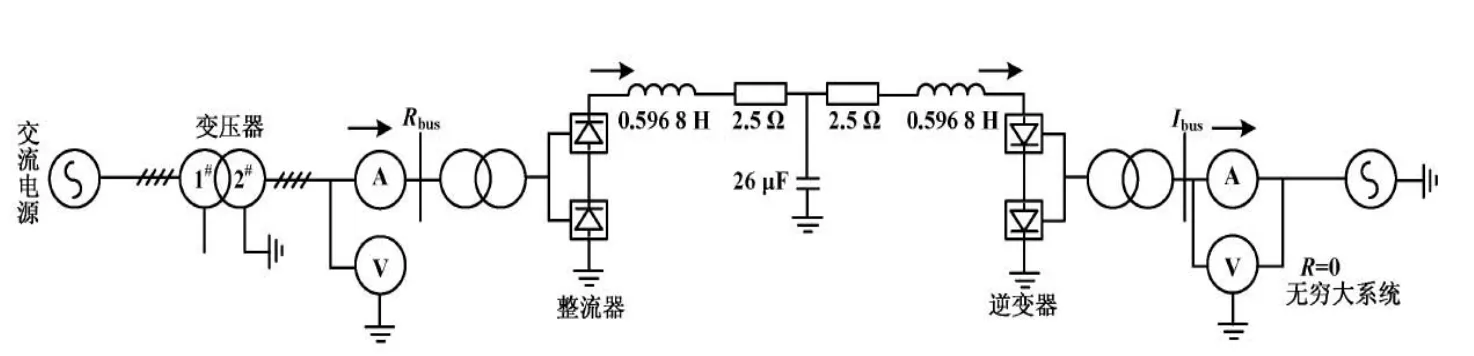
圖2 高壓直流輸電PSCAD模型圖Fig.2 HVDC PSCAD model

發電機的額定功率為892.4 MV。采用IEEE第一標準測試模型參數。直流額定輸送功率為1 000 MV，額定電壓為500 kV。直流輸電線路采用T型連接、直流系統采用12脈動結構、換流器等間隔觸發；整流端采用定電流控制、逆變端采用定熄弧角控制。HP、IP、LPA、LPB、GEN分別代表汽輪發電機高壓缸、中壓缸、低壓缸A、低壓缸B和發電機軸段。

①發電機輸出端施加三相短路故障信號，持續0.1 s。未加入SSDC的軸系扭矩和轉速曲線如圖3、圖4所示。

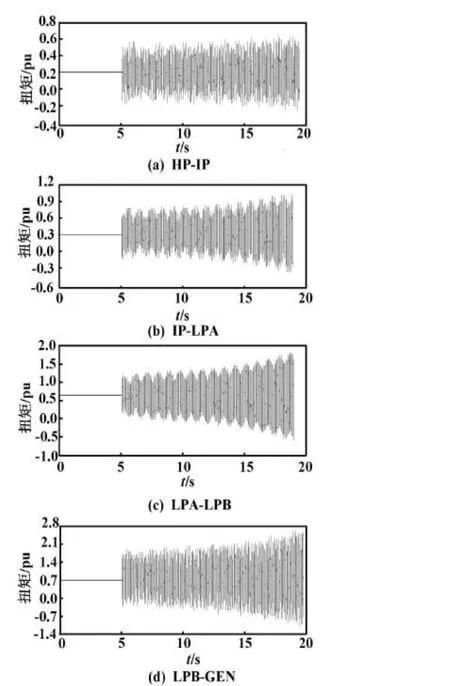
圖3 未加入SSDC的軸系扭矩曲線Fig.3 The shafting torque curves without SSDC

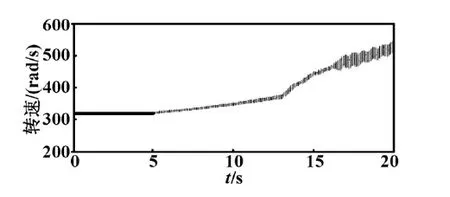
圖4 未加入SSDC的轉速曲線Fig.4 Rotating speed curve of shafting without SSDC

當系統發生大擾動，未加入附加阻尼控制器SSDC時，系統發生次同步振蕩。發電機各軸系呈發散狀態，發電機轉速呈現發散狀態。若不加以控制，將破壞發電機與輸電系統的穩定運行。

②發電機輸出端施加三相短路信號，持續0.1 s，加入SSDC的軸系扭矩和轉速曲線如圖5、圖6所示。

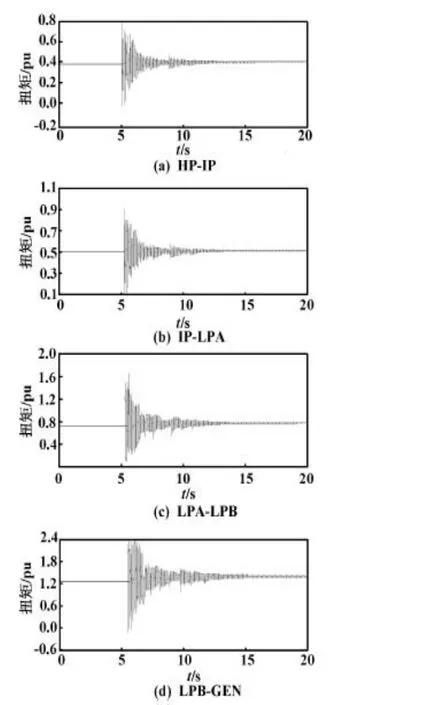
圖5 加入SSDC的軸系扭矩曲線Fig.5 The shafting torque curves with SSDC

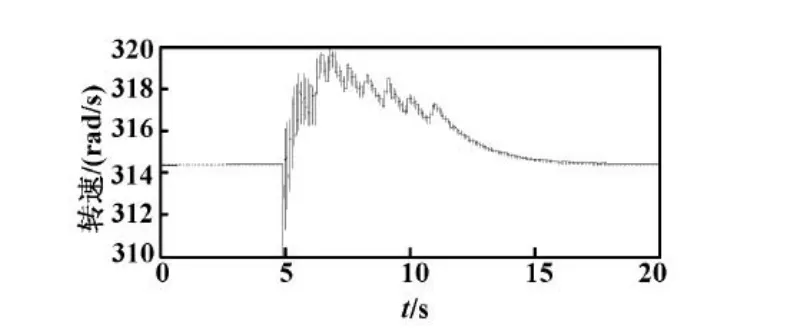
圖6 加入SSDC的轉速曲線Fig.6 Rotating speed curve of shafting with SSDC

加入附加阻尼控制器SSDC的輸電系統，能抑制系統次同步振蕩。發電機各軸系振蕩快速收斂，發電機轉速經波動后能恢復平穩。在一定范圍內，隨著SSDC放大倍數的增大，軸系振蕩收斂；軸系模態阻尼隨著增益系數的增大變強了，收斂速度變快。為了保證SSDC抑制SSO的有效性，SSDC相位補償環節要選取合適的相位補償度。在本模型中，SSDC增益系數取15～20、相位補償度取 40°～70°時，具有較好的控制性能。

4 結束語

對發電機軸系的扭振模態分析可知，在模態1（15.77 Hz）與模態 2（20.22 Hz）時特征值實部為正，阻尼比為負數，系統容易發生次同步振蕩。低壓缸與發電機軸段（LPB-LPA、LPA-GEN）負阻尼情況比較嚴重，軸段振蕩幅值較大。

根據特征值分析法對系統阻尼特性分析得知，狀態變量若沒出現在系統狀態矩陣的對角線上，則該參數不會對系統的總阻尼造成影響，且系統的總阻尼是恒定的。SSDC放大倍數能增強軸系模態阻尼，但阻尼值過大會引起系統其他模態發散，不利于振蕩的收斂。通過PSCAD仿真可知，SSDC選取適當的控制參數能有效抑制系統的次同步振蕩。

［1］劉振亞.中國電力與能源［M］.北京：中國電力出版社，2012.

［2］姜建國，顏廷閣.VSC-HVDC輸電系統的性能分析［J］.自動化儀表，2012，33（10）：5-8.

［3］張鵬，畢天姝.HVDC引起次同步振蕩暫態擾動風險的機理分析［J］.中國電機工程學報，2016，36（4）：961-968.

［4］劉順新，潘良勝，文振華.直流輸電換流站中的電流互感器配置研究［J］.自動化儀表，2014，35（10）：26-29.

［5］肖湘寧.電力系統次同步振蕩及其抑制方法［M］.北京：機械工業出版社，2014.

［6］吳俊勇，程時杰，陳德樹.用李雅普諾夫函數法判定汽輪發電機組軸系扭振的穩定性［J］.電力系統自動化，1997，21（7）：42-44.

［7］王晉.復轉矩系數法及次同步振蕩阻尼特性研究［D］.北京：華北電力大學，2011.

［8］高本鋒，趙成勇，肖湘寧.高壓直流輸電系統附加次同步振蕩阻尼控制器的設計與實現［J］.高電壓技術，2010，36（2）：501-506.

［9］唐釀，肖湘寧，李偉，等.HVDC附加次同步阻尼控制器設計及其相位補償分析［J］.高電壓技術，2011，37（4）：1015-1021.

［10］GUO C L，XIAO X N.The study of principle and applicability of complex torque coefficient approach［C］//International Conference，2011.

Torsional Vibration Analysis of Subsynchronous Oscillation in HVDC Transmission System

DANG Cunlu，YAN Zhanxiang，CHEN Lei
（College of Electrical and Information Engineering，Lanzhou University of Technology，Lanzhou 730050，China）

The traditional subsynchronous oscillation suppression method suppresses subsynchronous oscillation through blocking the interaction between mechanical system and electrical system by using damping filter.However，the adaptability of the damping filter to the environment is poor，the design parameters and operational maintenance are difficult.Therefore，the supplementary damping controller is added in the constant current system at the rectification terminal.The subsynchronous oscillation is suppressed by adjusting the system current and enhancing the modal damping of the shafting.This control method is effective，easy to control，and features good real time performance；and it doesn't affect the control performance of other controllers in the system.The transfer process of generator shafting eigenvalues，shafting modal damping，subsynchronous frequency component are analyzed，and then the relationship among the system control parameters，the mode of shafting and subsynchronous oscillation is studied.The supplementary damping controller which combines the generator speed deviation with the instantaneous voltage of the three-phase bus as input signal is designed.It can effectively reduce the output error of subsynchronous frequency conversion and improve the accuracy of the controller.The model parameters are studied by IEEE first standard，and the simulation model of subsynchronous oscillation of HVDC transmission is built in PSCAD.The simulation results show that the designed controller can effectively suppress subsynchronous oscillation of the system.

HVDC transmission；Subsynchronous oscillation；Eigenvalue analysis；SSDC；PSCAD

TH39；TP13

A

10.16086／j.cnki.issn1000-0380.201711006

修改稿收到日期：2017-06-08

黨存祿（1964—），男，學士，教授，主要從事電力電子及電氣傳動方向的研究。E-mail：dcl1964@163.com。嚴占想（通信作者），男，在讀碩士研究生，主要從事高壓直流輸電次同步振蕩的研究。E-mail：416514268@qq.com。