基于溫度變化Fourier展開的慣導(dǎo)航向效應(yīng)補(bǔ)償

何虔恩，楊功流，張 嶸，吳秋平

（1.福州大學(xué) 物理與信息工程學(xué)院，福州 350116；2.北京航空航天大學(xué) 儀器科學(xué)與光電工程學(xué)院，北京 100191；3.清華大學(xué) 精密儀器系，北京 100084）

基于溫度變化Fourier展開的慣導(dǎo)航向效應(yīng)補(bǔ)償

何虔恩1，楊功流2，張 嶸3，吳秋平3

（1.福州大學(xué) 物理與信息工程學(xué)院，福州 350116；2.北京航空航天大學(xué) 儀器科學(xué)與光電工程學(xué)院，北京 100191；3.清華大學(xué) 精密儀器系，北京 100084）

航向效應(yīng)對(duì)高精度空間穩(wěn)定平臺(tái)式慣性導(dǎo)航系統(tǒng)具有致命的影響。根據(jù)系統(tǒng)變航向?qū)Ш皆囼?yàn)數(shù)據(jù)，分析了變航向引起溫度及平臺(tái)漂移變化的作用機(jī)理，討論了平臺(tái)漂移變化與溫度變化的相關(guān)性，進(jìn)而提出基于溫度變化Fourier展開的航向效應(yīng)補(bǔ)償方法。采用滑動(dòng)最小二乘擬合導(dǎo)航誤差的方法提取平臺(tái)常值漂移的變化，并以此為觀測(cè)量標(biāo)定平臺(tái)漂移的溫度系數(shù)。最后，利用多組變航向試驗(yàn)數(shù)據(jù)對(duì)所述補(bǔ)償方法進(jìn)行驗(yàn)證，結(jié)果表明：平臺(tái)常值漂移變化與溫度變化基波分量的幅值具有強(qiáng)相關(guān)性，該補(bǔ)償方法可將溫度變化引起的航向效應(yīng)誤差降低40%～90%，具有較強(qiáng)的工程應(yīng)用潛力。

慣性導(dǎo)航系統(tǒng)；航向效應(yīng)；溫度變化；Fourier展開

慣導(dǎo)航向效應(yīng)主要表現(xiàn)為：在系統(tǒng)一次啟動(dòng)工作過(guò)程中，隨著航向角變化，導(dǎo)航精度發(fā)生不同程度的下降，嚴(yán)重時(shí)可使系統(tǒng)性能超差。因此，必須采取有效措施解決這一問(wèn)題。航向效應(yīng)大致可分為兩類：

1）原理性航向效應(yīng)。例如，在光纖陀螺尋北儀中[1]，從理論上可分析出，其尋北精度隨初始方位角變化呈正余弦形式變化；又如，在單軸旋轉(zhuǎn)慣導(dǎo)系統(tǒng)中[2]，載體航向運(yùn)動(dòng)與系統(tǒng)旋轉(zhuǎn)運(yùn)動(dòng)耦合影響了誤差調(diào)制效果，從而導(dǎo)致系統(tǒng)的“航向耦合效應(yīng)”，這類航向效應(yīng)易于進(jìn)行解析分析并從理論上提出相應(yīng)的解決方案。

2）隨機(jī)性航向效應(yīng)。導(dǎo)致這類航向效應(yīng)的因素錯(cuò)綜復(fù)雜且隨機(jī)多變，主要有伺服零位誤差、結(jié)構(gòu)擾動(dòng)力矩、線振動(dòng)、溫度場(chǎng)和電磁場(chǎng)變化等[3]，其中，溫度變化可能使伺服零位誤差發(fā)生變化，從而導(dǎo)致航向效應(yīng)[4]。

針對(duì)半球諧振陀螺平臺(tái)慣導(dǎo)系統(tǒng)初始對(duì)準(zhǔn)過(guò)程中存在的航向效應(yīng)的問(wèn)題，李彬等[4]研究探討了航向效應(yīng)誤差自標(biāo)定與補(bǔ)償方案，取得良好的實(shí)際補(bǔ)償效果。類似地，針對(duì)溫度變化引起的航向效應(yīng)（簡(jiǎn)稱溫度航向效應(yīng)）問(wèn)題，Cao H L等[5]提出一種基于熱敏電阻電路的溫度自動(dòng)補(bǔ)償方法，可將MEMS（微機(jī)電系統(tǒng)）陀螺標(biāo)度因數(shù)和零偏的溫度敏感性降低59%～60%。此外，還有增加溫控和改進(jìn)結(jié)構(gòu)設(shè)計(jì)等硬件手段[6]。

以上從硬件方面入手對(duì)付溫度航向效應(yīng)問(wèn)題常受結(jié)構(gòu)尺寸、時(shí)間和成本等因素的制約而難以實(shí)施，采用軟件方法可避免這一困難且可達(dá)到與硬件方法相當(dāng)?shù)男Ч蚨饛V大學(xué)者的研究興趣[6-10]。

溫度航向效應(yīng)軟件補(bǔ)償法的關(guān)鍵在于誤差建模，例如：針對(duì)快速、隨機(jī)溫變的環(huán)境，潘獻(xiàn)飛等[7]在進(jìn)行大量實(shí)驗(yàn)的基礎(chǔ)上提出基于溫度變化、溫變速率和溫度梯度的三次多項(xiàng)式模型；在光纖陀螺旋轉(zhuǎn)調(diào)制慣導(dǎo)的應(yīng)用中，Gao Pengyu等[9]提出基于框架旋轉(zhuǎn)角正余弦函數(shù)的航向效應(yīng)誤差模型及相應(yīng)的四位置標(biāo)定方案。多項(xiàng)式模型簡(jiǎn)單、易于實(shí)現(xiàn)，但擬合精度低，因此，有學(xué)者提出基于最小二乘-支持向量機(jī)（LS-SVM）[8]的溫度建模與補(bǔ)償方法。LS-SVM法因涉及大量的指數(shù)運(yùn)算，計(jì)算量大，實(shí)時(shí)性差，有學(xué)者進(jìn)一步提出分段線性擬合[6,10]的建模思想。縱觀公開文獻(xiàn)，溫度航向效應(yīng)誤差的建模本質(zhì)上是一個(gè)尋找誤差與溫度信息（包括溫度變化、溫變速率和溫度梯度等）之間定量關(guān)系的過(guò)程，由于誤差傳播特性復(fù)雜，目前，尚無(wú)可用的數(shù)理工具來(lái)解析求解這一定量關(guān)系，因而只能依賴于實(shí)驗(yàn)數(shù)據(jù)。

公開文獻(xiàn)討論的應(yīng)用對(duì)象集中在基于激光陀螺和MEMS陀螺的捷聯(lián)式慣性導(dǎo)航系統(tǒng)方面，以靜止水平基座條件下已知的地球自轉(zhuǎn)角速度矢量為參考信息，陀螺漂移可直接觀測(cè)。然而，對(duì)于空間穩(wěn)定平臺(tái)式慣導(dǎo)系統(tǒng)（簡(jiǎn)稱空間穩(wěn)定系統(tǒng)），平臺(tái)是空間穩(wěn)定的，其漂移只能通過(guò)比力或靜止水平基座條件下的框架角信息間接地獲取。另外，由于地球自轉(zhuǎn)，平臺(tái)相對(duì)系統(tǒng)殼體是連續(xù)旋轉(zhuǎn)的，其附近的溫度場(chǎng)變化規(guī)律與捷聯(lián)式慣導(dǎo)是截然不同的，相應(yīng)的溫度航向效應(yīng)特性也是不同的。因此，欲從軟件方面補(bǔ)償空間穩(wěn)定系統(tǒng)的溫度航向效應(yīng)，需另辟途徑，這是本文的出發(fā)點(diǎn)。

1 溫度航向效應(yīng)問(wèn)題剖析

對(duì)于空間穩(wěn)定系統(tǒng)，當(dāng)載體處于某一姿態(tài)時(shí)，穩(wěn)定平臺(tái)相對(duì)四環(huán)框架的幾何位置變化具有周期性（約為24 h），平臺(tái)與外界的熱量交換程度隨幾何位置的不同而不同，因而平臺(tái)溫度將隨之發(fā)生周期性波動(dòng)，如圖1的上圖所示。這一波動(dòng)周期大于平臺(tái)的熱傳導(dǎo)時(shí)間常數(shù)（根據(jù)每次啟動(dòng)期間的平臺(tái)溫度曲線，約12 h），使平臺(tái)上核心部件的溫度也是波動(dòng)的，而溫度變化又將引起機(jī)械結(jié)構(gòu)、慣性敏感元件的電路參數(shù)和光學(xué)特性等發(fā)生變化，進(jìn)而導(dǎo)致平臺(tái)漂移的變化，如圖1的下圖所示（平臺(tái)漂移的提取方法見第2節(jié)）。

圖1 溫度變化與平臺(tái)常值漂移歸一化對(duì)照曲線（示例）Fig.1 Normalized temperature variation and constant drift of platform (example)

在初始對(duì)準(zhǔn)與標(biāo)定期間，由平臺(tái)溫度24 h周期性波動(dòng)引起的平臺(tái)漂移已被綜合到最終的標(biāo)定結(jié)果中。在系統(tǒng)進(jìn)入導(dǎo)航模式后，若由于載體姿態(tài)改變（尤其是航向發(fā)生大角度變化）等因素導(dǎo)致平臺(tái)溫度24 h周期波動(dòng)規(guī)律發(fā)生變化，則平臺(tái)漂移將發(fā)生相應(yīng)變化，從而引起導(dǎo)航誤差。仍然以圖1為例：在第0～110 h，航向A跟初始對(duì)準(zhǔn)與標(biāo)定期間相同，平臺(tái)溫度24 h周期波動(dòng)規(guī)律一致重復(fù)，平臺(tái)漂移在零附近波動(dòng)；而當(dāng)航向由A切換到B（第110～158 h）或由B切換到C（第158 h ～192 h）之后，溫度曲線的波形改變了或者說(shuō)周期波動(dòng)的相位發(fā)生了變化，平臺(tái)漂移的平均值隨之發(fā)生較大的變化。即平臺(tái)漂移的變化與平臺(tái)溫度24 h周期波動(dòng)規(guī)律緊密相關(guān)，但兩者顯然不是簡(jiǎn)單的多項(xiàng)式關(guān)系。下面著重探討這種溫度航向效應(yīng)的建模與補(bǔ)償方法。

2 基于溫度變化Fourier展開的補(bǔ)償方法

溫度航向效應(yīng)的補(bǔ)償思路如下：

第一步，提取航向效應(yīng)和溫度變化信息；

第二步，建立航向效應(yīng)與溫度變化的定量關(guān)系；

第三步，利用第二步得到的關(guān)系，根據(jù)溫度變化實(shí)時(shí)修正有關(guān)參數(shù)，達(dá)到補(bǔ)償溫度航向效應(yīng)目的。

本節(jié)重點(diǎn)討論前兩步內(nèi)容。

2.1 航向效應(yīng)信息提取

航向效應(yīng)最終體現(xiàn)在導(dǎo)航誤差上，因而本質(zhì)上可由平臺(tái)失準(zhǔn)角、漂移參數(shù)和加速度計(jì)誤差來(lái)表征。其中，加速度計(jì)誤差，從比力模檢驗(yàn)結(jié)果知，在變航向條件下可忽略不計(jì)。此時(shí)，導(dǎo)航誤差主要與平臺(tái)失準(zhǔn)角和漂移參數(shù)有關(guān)[11]：

情境認(rèn)知理論認(rèn)為，學(xué)習(xí)設(shè)計(jì)要以學(xué)生為主體，學(xué)習(xí)內(nèi)容與學(xué)習(xí)活動(dòng)的安排要與人類的具體社會(huì)實(shí)踐相聯(lián)通，通過(guò)真實(shí)實(shí)踐的方式在真實(shí)的情景中組織教學(xué)，同時(shí)把知識(shí)、能力的獲得與學(xué)生的未來(lái)發(fā)展、身份建構(gòu)等整合在一起。

緯度誤差：

經(jīng)度誤差：

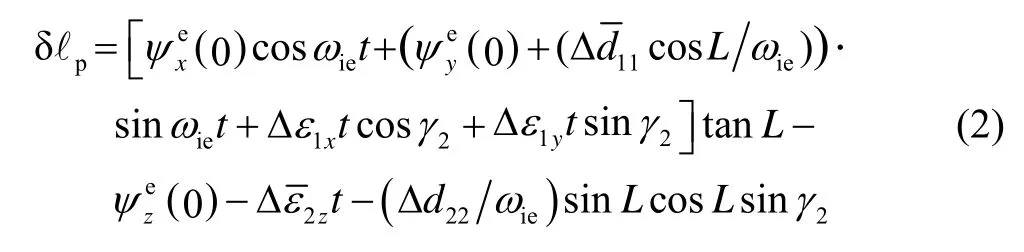
由式(1)和(2)易見，聯(lián)立2γ變化360°（t變化約24 h）對(duì)應(yīng)的緯度和經(jīng)度誤差序列，即可分離出各誤差項(xiàng)的系數(shù)。因此，可利用當(dāng)前時(shí)刻以前24 h（擬合窗寬度）以內(nèi)的緯度和經(jīng)度誤差估計(jì)對(duì)應(yīng)的平臺(tái)失準(zhǔn)角和漂移參數(shù)，作為當(dāng)前時(shí)刻航向效應(yīng)的信息量。

2.2 溫度變化及其Fourier展開

根據(jù)第1節(jié)的分析知，平臺(tái)溫度波動(dòng)的周期性主要源自平臺(tái)相對(duì)四環(huán)框架的幾何位置變化的周期性，而這一周期正是2γ變化360°對(duì)應(yīng)的時(shí)間長(zhǎng)度。因此，可取初始對(duì)準(zhǔn)與標(biāo)定期間2γ變化360°的最后一段溫度序列作為參考溫度，并將導(dǎo)航期間每一時(shí)刻的溫度與對(duì)應(yīng)的參考溫度（2γ相差360°的整數(shù)倍）相減，得到溫度變化曲線ΔTg(t)。顯然，當(dāng)溫度變化處于穩(wěn)態(tài)時(shí)，ΔTg(t)也具有周期性，且周期等于2γ變化360°對(duì)應(yīng)的時(shí)間長(zhǎng)度。此時(shí)，對(duì)ΔTg(t)進(jìn)行Fourier級(jí)數(shù)展開：

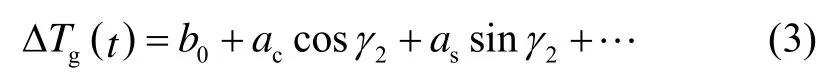
這樣，溫度變化的信息可由b0、ac和as等系數(shù)表征。為了提取這些系數(shù)，可采用類似于前面航向效應(yīng)信息提取的方法：對(duì)當(dāng)前時(shí)刻以前24 h以內(nèi)的溫度變化曲線按式(3)進(jìn)行最小二乘擬合，得到各項(xiàng)系數(shù)估計(jì)值，作為當(dāng)前時(shí)刻溫度變化的信息。

2.3 溫度航向效應(yīng)補(bǔ)償模型

由式(1)和(2)可見，平臺(tái)常值漂移引起的定位誤差是隨時(shí)間積累的，因而對(duì)導(dǎo)航精度具有致命影響；另外，鑒于平臺(tái)熱傳導(dǎo)時(shí)間常數(shù)約12 h，因而略去ΔTg(t)二次以上的諧波分量，且只考慮平臺(tái)常值漂移的修正：

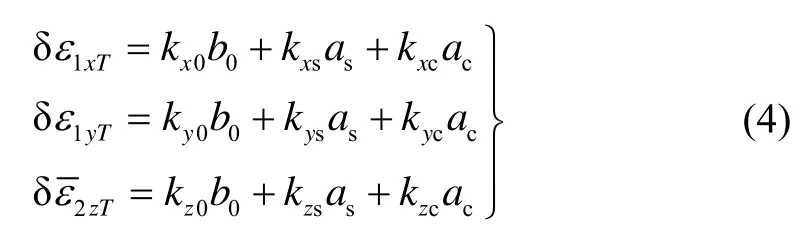
2.4 分析討論

在航向效應(yīng)信息提取時(shí)，減小擬合窗寬度可提高信息提取的時(shí)間分辨率，能很快捕捉到信息的變化，但降低了信噪比；反之，增大擬合窗寬度可提高穩(wěn)態(tài)信息提取的精度，但不能及時(shí)捕捉到信息的變化。因此，為了準(zhǔn)確標(biāo)定模型參數(shù)：一方面，擬合窗寬度應(yīng)足夠長(zhǎng)，根據(jù)式(1)和(2)所示的經(jīng)緯度誤差特性，并結(jié)合實(shí)踐經(jīng)驗(yàn)，其寬度取為24 h較合適；另一方面，應(yīng)盡量延長(zhǎng)相鄰兩次變航向的時(shí)間間隔，使航向效應(yīng)信息保持在穩(wěn)態(tài)的時(shí)間足夠長(zhǎng)，這一時(shí)間間隔至少為平臺(tái)熱傳導(dǎo)時(shí)間常數(shù)與擬合窗寬度之和。

另外，由于平臺(tái)存在一定的熱傳導(dǎo)時(shí)間常數(shù)τ，平臺(tái)漂移參數(shù)的變化相對(duì)平臺(tái)溫度變化會(huì)有一定的滯后，若以前者為輸出，后者為輸入，則中間相當(dāng)于經(jīng)過(guò)了一個(gè)帶寬約為1/τ的低通濾波器。這樣，利用式(4)的補(bǔ)償模型，根據(jù)溫度變化直接對(duì)平臺(tái)漂移參數(shù)進(jìn)行修正將不會(huì)有延遲的問(wèn)題，同時(shí)，對(duì)于由載體短周期搖擺等因素引起的平臺(tái)溫度快速變化還有過(guò)濾作用。

3 試驗(yàn)結(jié)果

3.1 補(bǔ)償模型標(biāo)定結(jié)果

利用系統(tǒng)某次導(dǎo)航期間航向變化三次以上（相鄰兩次間隔大約兩晝夜）的試驗(yàn)數(shù)據(jù)，按第2節(jié)所述方法提取航向效應(yīng)和溫度變化的信息。取其中三個(gè)不同航向?qū)?yīng)的穩(wěn)態(tài)數(shù)據(jù)，代入式(4)，可得到9個(gè)獨(dú)立的代數(shù)方程，聯(lián)立求解可得平臺(tái)常值漂移的9個(gè)溫度系數(shù)，結(jié)果如下：

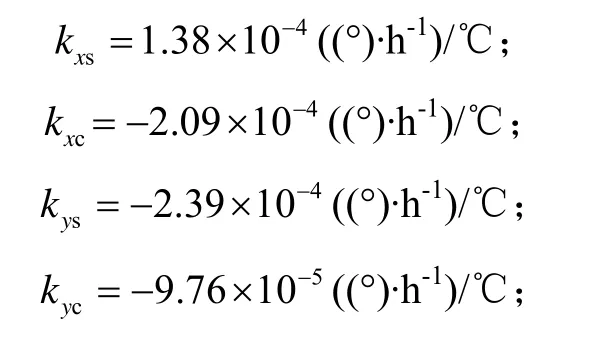
其余五個(gè)系數(shù)量級(jí)較小，可忽略不計(jì)。

3.2 變航向試驗(yàn)結(jié)果

利用第3.1節(jié)模型標(biāo)定結(jié)果，在多組變航向試驗(yàn)中按照式(4)實(shí)施溫度航向效應(yīng)補(bǔ)償。圖2和圖3分別摘錄了某組變航向試驗(yàn)實(shí)施補(bǔ)償前后的導(dǎo)航經(jīng)度誤差和緯度誤差曲線。易見，實(shí)施補(bǔ)償后，導(dǎo)航誤差對(duì)航向變化的敏感性比實(shí)施補(bǔ)償前降低了40%～90%。其它幾組變航向試驗(yàn)也達(dá)到同樣的效果。

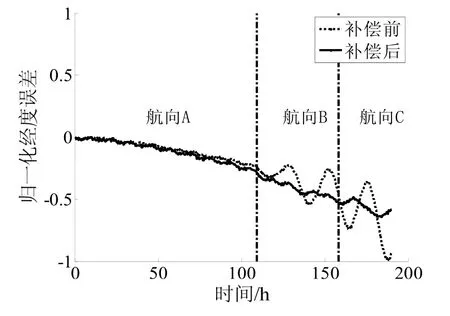
圖2 實(shí)施溫度航向效應(yīng)補(bǔ)償前/后的經(jīng)度誤差Fig.2 Longitude errors before/after the compensation of heading effect due to temperature variations

圖3 實(shí)施溫度航向效應(yīng)補(bǔ)償前/后的緯度誤差Fig.3 Latitude errors before/after the compensation of heading effect due to temperature variations

另外，從圖2和圖3可見，經(jīng)補(bǔ)償后導(dǎo)航誤差中仍殘余一些與航向有關(guān)的分量，主要表現(xiàn)為等幅振蕩形式，這可能是由于在不同的航向角位置，框架的摩擦力矩、電場(chǎng)干擾和磁場(chǎng)干擾等非溫度因素發(fā)生了變化以及未考慮平臺(tái)失準(zhǔn)角變化所造成的航向效應(yīng)。幸好，這部分殘余分量不是隨時(shí)間積累的，且量級(jí)較小，在實(shí)踐中可暫不考慮對(duì)之實(shí)施補(bǔ)償。

4 結(jié) 論

針對(duì)空間穩(wěn)定平臺(tái)式慣性導(dǎo)航系統(tǒng)的航向效應(yīng)問(wèn)題，從系統(tǒng)變航向?qū)Ш皆囼?yàn)結(jié)果入手，分析了變航向引起溫度及平臺(tái)漂移變化的機(jī)理，并提出一種基于溫度變化Fourier展開的航向效應(yīng)軟件補(bǔ)償方法。試驗(yàn)結(jié)果表明：平臺(tái)常值漂移變化與溫度變化基波分量的幅值具有強(qiáng)相關(guān)性；采用所述軟件補(bǔ)償方法后，導(dǎo)航誤差對(duì)航向變化的敏感性比補(bǔ)償前降低了40%～90%；補(bǔ)償方法簡(jiǎn)便易行，為緩解溫度航向效應(yīng)問(wèn)題提供一種技術(shù)手段，具有工程應(yīng)用價(jià)值。

（References）：

[1]張馨, 王宇, 程向紅.光纖陀螺尋北儀航向效應(yīng)誤差分析和補(bǔ)償[J].彈箭與制導(dǎo)學(xué)報(bào), 2010, 30(5): 54-58.Zhang X, Wang Y, Cheng X H.Error analysis and compensation of heading effect for FOG north-seeker[J].Journal of Projectiles, Rockets, Missiles and Guidance,2010, 30(5): 54-58.

[2]許江寧, 查峰, 李京書, 等.單軸旋轉(zhuǎn)慣導(dǎo)系統(tǒng)“航向耦合效應(yīng)”分析與補(bǔ)償[J].中國(guó)慣性技術(shù)學(xué)報(bào), 2013,21(1): 26-30.Xu J N, Zha F, Li J S, et al.Analysis and compensation for heading-coupling effect of single-axis rotating INS[J].Journal of Chinese Inertial Technology, 2013, 21(1): 26-30.

[3]Huang X K, Chen Y X, Kang R.Research on heading sensitive drift behavior of inertial platform system under long-term storage condition[J].Journal of Aeronautics &Aerospace Engineering, 2012, 1(1): 1-7.

[4]李彬, 劉潔瑜, 陳偉.半球諧振陀螺平臺(tái)航向效應(yīng)誤差研究[J].電光與控制, 2016, 23(12):65-70.Li B, Liu J Y, Chen W.Heading effect error of hemisphere resonator gyro platform[J].Electronics Optics &Control, 2016, 23(12): 65-70.

[5]Cao H L, Li H S, Sheng X, et al.A novel temperature compensation method for a MEMS gyroscope oriented on a periphery circuit[J].International Journal of Advanced Robotic Systems, 2013, 327(10): 1-10.

[6]Li J, Ma Y, Chen X Y.Error modeling, calibration, and nonlinear interpolation compensation method of ring laser gyroscope inertial navigation system[J].Abstract and Applied Analysis, 2013: 1-7.

[7]潘獻(xiàn)飛, 楊杰, 吳美平.復(fù)雜溫變環(huán)境下的激光陀螺零偏補(bǔ)償方法[J].中國(guó)慣性技術(shù)學(xué)報(bào), 2011, 19(2): 234-238.Pan X F, Yang J, Wu M P.RLG bias compensation method in complex temperature variation environment[J].Journal of Chinese Inertial Technology, 2011, 19(2): 234-238.

[8]Song R, Chen X, Tang C.Study on temperature drift modeling and compensation of FOG based on AFSA optimizing LS-SVM[C]// Guidance, Navigation and Control Conference.IEEE, 2015: 538-542.

[9]Gao P Y, Li K, Wang L, et al.Four-position heading effect calibration algorithm for rotation inertial navigation system based on fiber optic gyro[J].Optical Engineering,2016, 55(7): 1-10.

[10]Cheng J C, Fang J C.Comparison of compensation methods on RLG temperature error and their application in POS[C]//Proceedings of the 2012 8th IEEE International Symposium on Instrumentation and Control Technology.2012: 189-194.

[11]高鐘毓.慣性導(dǎo)航系統(tǒng)技術(shù)[M].北京: 清華大學(xué)出版社, 2012: 285-287.Gao Z Y.Inertial navigation systems technology[M].Beijing: Tsinghua University Press, 2012: 285-287.

Compensation method of heading effect for inertial navigation system based on Fourier decomposition of temperature variation

HE Qian-en1, YANG Gong-liu2, ZHANG Rong3, WU Qiu-ping3
(1.School of Physics and Information Engineering, Fuzhou University, Fuzhou 350116, China;2.School of Instrumentation Science & Opto-electronics Engineering, Beihang University, Beijing 100191,China; 3.Department of Precision Instruments, Tsinghua University, Beijing 100084, China)

Heading effect is one of the most challenging problems of high accuracy space-stable platform inertial navigation systems.With system heading changing experiment data, the affection theory of heading changing to variations of temperature and platform drift is analyzed, and the relationship between platform drift variation and temperature variation is discussed.In sequence, a compensation method of heading effect based on Fourier decomposition of temperature variation is proposed.Moving least-squares fitting of navigation errors is adopted to withdraw the actual series of platform constant drift, which are thereafter the observations for calibrating temperature coefficients of platform drift.Multiple heading changing experiments are conducted to verify the proposed method.The results show that there exists strong correlation between platform constant drift variation and the amplitudes of fundamental wave of temperature variation, and the heading effect errors due to temperature variation may be reduced by 40% to 90% with the proposed compensation method, which has significant potential for engineering application.

inertial navigation systems; heading effect; temperature variation; Fourier decomposition

U666.1

A

1005-6734(2017)05-0581-04

10.13695/j.cnki.12-1222/o3.2017.05.005

2017-06-10；

2017-09-18

總裝“十二五”預(yù)研項(xiàng)目（51309030401）

何虔恩（1985—），男，講師，從事導(dǎo)航系統(tǒng)與控制研究。E-mail: heqianen2005@126.com

聯(lián) 系 人：吳秋平（1972—），男，副研究員，博士生導(dǎo)師。E-mail: wuqiuping@mail.tsinghua.edu.cn