改進的濕模態法在流固耦合中的應用

劉瑞駿， 郝志勇， 鄭 旭， 談江林

(浙江大學 能源工程學院，杭州 310027)

改進的濕模態法在流固耦合中的應用

劉瑞駿， 郝志勇， 鄭 旭， 談江林

(浙江大學 能源工程學院，杭州 310027)

針對流固耦合運動方程，指出了流體剛度矩陣的奇異性將導致現有的濕模態法無法直接使用，并指出了在濕模態法中使用分離零頻項的方法存在的矛盾。濕模態法的問題根源在于為了簡化計算而提出的不合理的前提假設，即同時忽略流體的可壓縮性及自由液面波動的影響；據此，提出了直接求解法和不動點法兩種解決方法；前者適合流體規模較小的計算，而后者更適合大規模流體的耦合計算；應用不動點法，編制了Matlab程序，對某油底殼在不同盛油狀態時的結構特性進行了仿真計算，對比表明隨著盛油量從0逐步增加，結構模態頻率呈先減小后增大的趨勢并趨于平緩；加入流體后，結構模態的振幅大幅下降。除了第1階模態，流體較少時的濕模態振型與干模態振型區別較大，但隨著流體的增加，振型逐漸趨于穩定，與干模態振型接近。

流固耦合；濕模態；直接求解法；不動點法

與流體相接觸的結構在發生振動時，其周圍流場也會同時產生變化。這種流場的變化反過來會使得結構所受到的流體動力發生變化，形成反饋的流體-結構相互作用的流固耦合問題。在海洋、船舶、航空、水利等許多工程領域都存在此類流固耦合的振動問題。

當下，對于與流體的相對運動不大的結構，計算其流固耦合的結構特性時，通常可以把流體視為無黏、無旋的理想流體，采用的方法主要有虛質量法、附加質量法、邊界元法以及濕模態法[1-4]。Lewis等假定半沉入水中的圓柱體周圍的水流狀態與全沉入水中的相同，利用已知速度勢得到附加水質量的計算公式[5]。柳瑞鋒等[6]對比了虛質量法和附加質量法在計算船體低階濕模態時的誤差，結果表明兩種方法的精度均滿足工程要求，且虛質量法的計算過程更簡單，結果也較精確。吳紹亮等[7]使用流體邊界元法對船體局部結構的流體附加質量進行計算，與經驗公式法的對比表明兩者對于簡單結構均有足夠的工程計算精度，但對于復雜結構，經驗公式法的精度不如流體邊界元法。

為了提高計算結構動力響應時的效率，模態疊加法[8]是不錯的選擇，此時就需要利用固有模態矩陣進行坐標變換。當不考慮流體的影響時，計算所得的模態稱為干模態，而考慮了周圍流體影響的則稱為濕模態。濕模態法是最常使用的一種計算流固耦合振動特性的方法，現有的文獻中已大量報導了濕模態法的應用實例[9-15]。但是，實際應用過程中，此方法的使用卻存在一個不可忽視的問題，即流體剛度矩陣的奇異性。王勖成[16]提出使用分離流體零頻的方法來消除奇異性，方法本身是合理的，但本文將指出其使用過程中的矛盾，并提出濕模態法難以求解的根本原因及其解決方法。此外，本文將利用內燃機上常用的某個油底殼結構，計算不同盛油量對結構模態頻率及振型的影響。

1 濕模態法

1.1 一般表達形式

對于流固耦合的結構，其流體方程及邊界條件為

(1) 流體域內

(1)

式中：p為流體動壓力；c為流體內聲速。

對于不可壓縮流體，c→∞，則有

2p=0

(2)

(2) 流固耦合面上

(3)

(3) 固定界面上

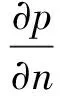
(4)

(4) 流體自由表面上

(5)

式中：z為重力方向；g為重力加速度。

為簡化后續計算，當不考慮流體自由表面的影響時，式(5)將改寫為

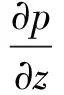
(6)

(5) 流體無限遠處

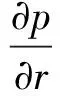
(7)

式中：r為足夠遠處邊界的法向；t為時間。

對于不可壓縮流體，有

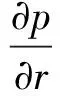
(8)

使用Galerkin法離散化后，直角坐標系內流場內任一點的壓力分布p(x,y,z,t)可近似表示為

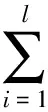
(9)

式中：l為流體單元節點數；N為流體單元形函數。

由有限元分析可知

?ΩNi(2p*)dΩ=0

(10)

式中，Ω為流體單元體積。若令

(11)

(12)

式中，k為流體域總節點數。則式(10)可擴展為

?ΩN(2p*)dΩ=0

(13)

對式(13)采用Green公式，可化為

(14)

將邊界條件及式(9)代入后，式(14)變為

?ΩN

(15)

式中，SI為流固耦合面積。

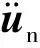
(16)

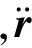
(17)

其中，

H=?ΩNNTdΩ

(18)

因其表達式與結構剛度矩陣具有相同的形式，故而稱為流體剛度矩陣。

(19)

式中，B為流固耦合矩陣。

另一方面，結構的運動方程表示為

(20)

式中，Ms、Cs、Ks分別為結構的質量矩陣、阻尼矩陣以及剛度矩陣；fp為流固耦合面上流體動壓力產生的激勵矢量；f0為其他外界激勵矢量。

利用虛位移法可得

fp=-BTp

(21)

因此，對于無阻尼結構，流固耦合中結構的運動方程為

(22)

聯立式(17)與式(22)，當考慮自由振動時，且q0=0，則有

(23)

求解式(23)，易得

(24)

(25)

其中，

Ma=ρBTH-1B

(26)

式中，Ma為流體附加質量。

利用一般多自由度線性系統的自由振動求解方法[17]，流固耦合中結構的模態與振型很容易通過式(25)獲得。

1.2 濕模態中的問題

計算流體附加質量需要用到式(26)，其中需要計算H的逆矩陣。然而，形函數的性質決定了被離散物體本身的剛度矩陣必須是奇異的。因此，流體剛度矩陣H是不可逆的，必須將流體剛度矩陣的奇異性消除才能求解式(23)～式(26)。

1.3 奇異性的消除方法及其問題

王勖成采用分離流體零頻的方法來消除H的奇異性，其中具體的公式推導本文不再復述。

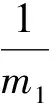
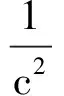
(27)

式中，SF為流體自由表面面積。可見，Mf由兩項構成，前一項由流體的可壓縮性引起，后一項由自由液面的波動引起。而回到問題最初的假設，流體是不可壓縮的且不考慮液面波動的影響，因此將假設后的邊界條件代入上式可得Mf=0，故而m1=0，m1出現在分母上是不合理的。

所以，此方法的應用前提是流體的可壓縮性和自由液面的影響不能同時忽略，即Mf≠0，此時式(23)必須改寫為

(28)

其中式(28)中第二式為

(29)

然而此時，流體剛度矩陣H奇異與否已經不影響進一步的計算了。

2 求解濕模態的方法

通過“1”節已經了解到，當前提假設為流體不可壓縮且不考慮自由液面波動的影響時，H為奇異矩陣，直接求解式(23)或是通過“1.3”節的分離零頻的方法都是不可取的。因此濕模態法的根本問題在于為了簡化計算而提出了錯誤假設。事實上，當同時假設了流體的不可壓縮性，以及忽略自由液面的影響，流體域處于完全自由邊界的條件下，在結構激勵下會表現出類似結構剛體運動的響應形式。對此，本文將給出兩種解決方法。

2.1 直接求解法

考慮流體的可壓縮性以及自由液面波動的影響，則對于無阻尼系統，流固耦合方程應采用式(28)表達。采用復指數法[18]，令r=Rejωt，p=Pejωt并代入式(28)，則

(30)

求解式(30)的第二式可得

P=ρω2(H-ω2Mf)-1BR

(31)

代入式(30)的第一式得

[ω2Ms-Ks+ρω2BT(H-ω2Mf)-1B]R=0

(32)

令

A(ω)=ω2Ms-Ks-ρω2BT(H-ω2Mf)-1B

(33)

則式(32)有非零解的唯一條件是A(ω)的行列式為零，即

det[ω2Ms-Ks+ρω2BT(H-ω2Mf)-1B]=0

(34)

求解式(34)可求得所有的特征值及特征向量，進而獲得模態頻率及振型。

由于矩陣的行列式為零等價于至少存在一個特征值為零的特征向量，可令其為x。考慮以下問題

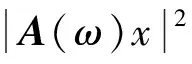
(35)

式(34)的解一定是這個問題的解。這個問題中沒有行列式，只有矩陣向量的運算，是一個約束優化問題[19]，采用拉格朗日乘子法即可求解[20]。

考慮到A(ω)中包含了(H-ω2Mf)-1，此逆矩陣的階數等于流體域的節點數，且ω作為未知參數被代入求逆矩陣，因此僅當流體域較小時，此方法較為適用。

2.2 不動點法

對于節點數較多的流體域，“2.1”節所采用的直接求解法就難以適用了。為了仍能通過式(23)～式(26)求解流固耦合方程，則可依然在流體不可壓縮和忽略自由液面影響的前提假設下，于流體域內假定一個不動點，此點的流體動壓力恒為零，等效于對流體進行了約束。實際處理過程中，可采用大數法，然后通過式(23)～式(26)即可求解耦合運動方程。

這個不動點最好選取在流固耦合面上且結構節點位移為零處，此處流體動壓也為零，又由于靜壓對結構振動不產生影響，因此這樣的節點最適合作為不動點。如果不存在這樣的節點，則可在無限遠處或自由表面選取一點，對于大型的、節點數較多的復雜流體域，由于約束的區域相對很小，因此同樣可以滿足精度要求。

3 仿真計算

采用Matlab編程的方法，對內燃機中常用的某油底殼進行仿真計算，如圖1(a)所示。令最多盛油量時油液高度為h(h=69 mm)，則圖1(b)～圖1(e)分別代表油液高度為h/4、h/2、3h/4以及h時的狀態。

圖1 不同盛油量時的油底殼Fig.1 The oil pans with different oil mass

油底殼采用三角形殼單元建立，油液采用一階四面體單元建立，具體參數如表1所示。

表1 計算模型參數

由于流體節點數較多，因此采用直接求解法較為困難，此處采用不動點法進行計算，約束節點為流體自由表面某一點。表2與圖2為5種油底殼狀態前5階模態頻率(去除剛體模態)對比。

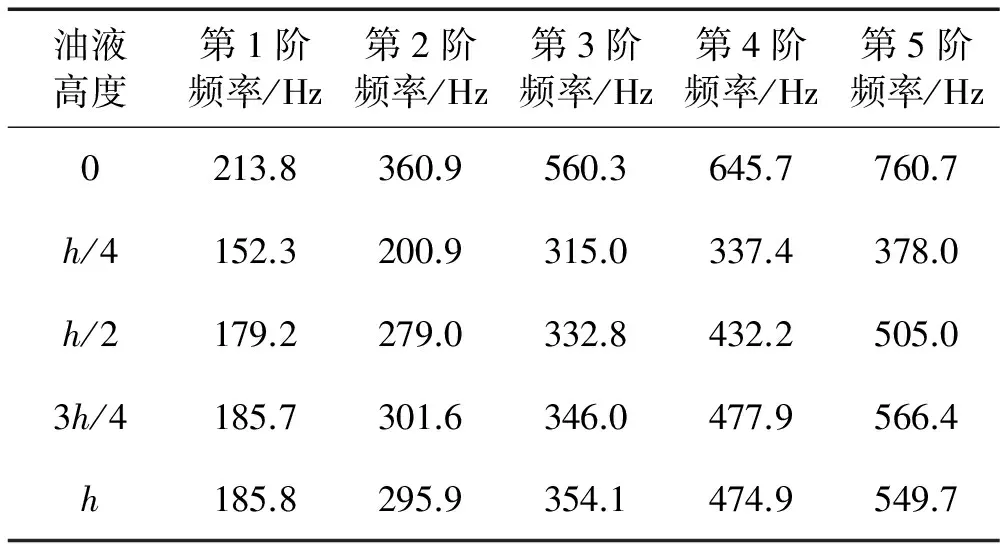
表2 不同油液高度下前5階模態頻率

由圖2可知，當盛油量逐漸增加時，油底殼的前5階模態頻率基本呈現先減小后增大的趨勢，并趨于平緩，這與張亮等[21]中所得結論并不一致，可能是由于油底殼結構不同而導致的。由式(26)可知，附加質量矩陣取決于H及B，而由B的表達式可以看到對它產生影響的不止有流體、固體的形函數，還有坐標變換矩陣，它是由耦合面的大小、形狀、方向等幾何特征共同決定的。這也同樣說明，流體越多，附加的質量越大，耦合結構模態頻率越低的說法并不是一定成立的。

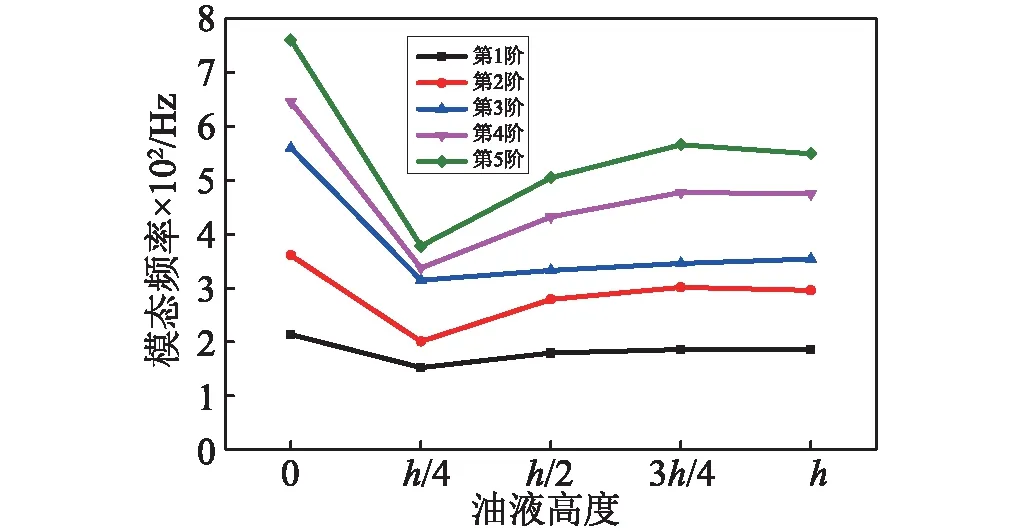
圖2 不同油液高度下前5階模態頻率Fig.2 The first 5 order modal frequencies with different oil height

另一方面，從宏觀上來說，模態頻率取決于結構的質量與剛度，因此由圖2也可以推斷出，對于本文所使用的油底殼結構，當耦合系統中僅有少量流體時，流體的影響僅體現在附加的質量上，而當流體增多時，附加質量增加的同時，流體附加的剛度逐漸提高，因此導致了模態頻率回升的現象。

為了進一步驗證仿真計算的結論是可靠的，在圖1的基礎上將翻邊上的螺栓孔約束，通過試驗測取了油液高度為0、h/4、h/2、3h/4的油底殼約束模態，前10階模態頻率的對比，如圖3所示。

由圖3可知，隨著油液高度的增加，油底殼的約束模態頻率基本也呈現先減小后增大的趨勢，與自由模態有較好的一致性。

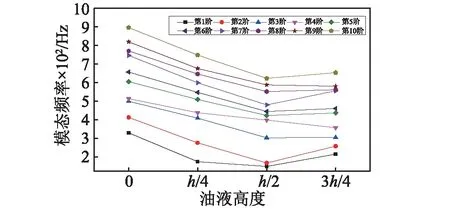
圖3 不同油液高度下前10階試驗模態頻率Fig.3 The first 10 order test modal frequencies with different oil height

圖4為圖2中5種油底殼盛油狀態前3階結構振型。其中，各個節點的絕對振幅以結構形變表示，相對振幅的范圍為0～1。

由圖4可知，從絕對振幅上看，圖4(d)～圖4(o)所呈現的結構形變都遠小于圖4(a)～圖4(c)；這表明，流體的加入在很大程度上抑制了結構模態的振幅。因此，結合表2與圖2，當進行到后續的動力學及聲學計算時，如果不將流體的影響計入，則將很有可能使油底殼的振-聲峰值頻率后移并放大振動及噪聲，導致出現不合理的仿真計算結果。

縱向對比每一階模態，除第1階振型在各種狀態下變化不大以外，第2階、第3階振型均在加入流體后產生了明顯的變化，如圖4(b)、圖4(c)與圖4(e)、圖4(f)的對比所示。并且，隨著盛油量的增加，振型趨于穩定，且較為接近不盛油狀態時的干模態振型。

圖4 5種油底殼狀態前3階結構振型Fig.4 The first 3 order structural modal shapes of the 5 oil pans

4 結 論

(1) 本文指出了濕模態法在應用時所遇到的問題，即流體剛度矩陣的奇異性。同時，指出了通過分離零頻來消除流體剛度矩陣奇異性的方法中存在的矛盾。這些問題說明了，濕模態法不能被直接使用的根本原因是錯誤的前提假設，即同時忽略了流體的可壓縮性以及流體自由表面的影響。

(2) 本文提出了兩種可行的濕模態法的計算方法。其中，直接求解法使用的前提是流體的可壓縮性和自由表面的影響不能被同時忽略，計算時可將行列式方程的問題轉化為約束二次優化問題，并采用拉格朗日乘子法求解，但該方法僅適用于規模較小的流體域。另一種方法為不動點法，此方法仍在原先的前提假設下，選取流體中的一點，令其動壓力恒為零，則可避免流體剛度矩陣無法求逆的問題并繼續使用濕模態法求解。不動點法更適用于大型、復雜的流體域，以保證局部約束給整體剛度帶來的影響較小。

(3) 本文采用不動點法對不同盛油量的某油底殼進行了模態計算。模態頻率的對比表明，隨著盛油量從0逐步增加，該油底殼的模態頻率呈先減小后增大的趨勢，并趨于平緩。通過與張亮等研究的結論對比，表明流體的增多并不一定使結構的模態頻率單調遞減，流體導致的模態頻率上的變化還取決于流固耦合面的幾何特征。對于該油底殼而言，當盛油量較少時，流體的影響以附加質量為主，隨著盛油量逐漸增多，附加質量增加的同時，附加剛度的作用逐漸體現。

(4) 不同盛油狀態時模態振型的對比表明，流體的加入很大程度上抑制了結構的模態振幅，結合頻率的變化說明，在進行流固耦合系統的結構特性、動力學以及聲學計算時有必要將流體的影響考慮在內，否則將導致峰值頻率的后移以及振-聲幅值的放大，以致不合理的計算結果。另外，縱向對比各階模態可見，隨著盛油量的增加，模態振型趨于穩定，并接近干模態振型。

[ 1 ] 陸鑫森. 高等結構動力學[M]. 上海: 上海交通大學出版社, 1992.

[ 2 ] 賈維新. 發動機結構噪聲和進氣噪聲的數字化仿真及優化設計研究[D]. 杭州: 浙江大學, 2008.

[ 3 ] 鄭運虎, 李穎. 立式圓柱薄殼容器的振動特性研究[J]. 西華大學學報(自然科學版)， 2016,35(1): 24-28.

ZHENG Yunhu, LI Ying. Research on the vibration characteristics of vertical cylindrical shell container [J]. Journal of Xihua University (Natural Science)， 2016,35(1): 24-28.

[ 4 ] 周勇, 車馳東. 水下航行器附連水質量的理論及實驗研究[J]. 上海交通大學學報, 2016,50(2): 176-181.

ZHOU Yong, CHE Chidong. Theoretical and experimental study of added mass for underwater vehicles [J]. Journal of Shanghai Jiao Tong University, 2016,50(2): 176-181.

[ 5 ] 孫洋. 附加水質量對船體總振動固有頻率影響的研究[D]. 大連: 大連理工大學, 2008.

[ 6 ] 柳瑞鋒, 黃嶸, 周相榮, 等. 船體低階濕模態計算方法對比研究[J]. 船舶工程， 2014(4): 25-28.

LIU Ruifeng, HUANG Rong, ZHOU Xiangrong, et al. Contrast study on calculation method for lower order wet mode of ship hull [J]. Ship Engineering, 2014(4): 25-28.

[ 7 ] 吳紹亮, 金咸定. 流固耦合計算方法在船舶局部結構中的應用[J]. 振動與沖擊, 2003,22(4): 28-30.

WU Shaoliang, JIN Xianding. Computation method for fluid / structure interaction in local structures of ship [J]. Journal of Vibration and Shock, 2003,22(4): 28-30.

[ 8 ] 李東旭. 高等結構動力學[M]. 北京: 科學出版社, 2010.

[ 9 ] 黃曉明, 朱錫, 牟金磊, 等. 整體結構模型低階濕模態仿真計算方法[J]. 艦船科學技術, 2011,33(5): 9-12.

HUANG Xiaoming, ZHU Xi, MU Jinlei, et al. Simulation and experimental investigation on transverse lower order wet mode of whole structure model [J]. Ship Science and Technology, 2011,33(5): 9-12.

[10] 王崢, 洪明, 劉城. 基于FEM/BEM的浸水結構振動及聲輻射特性國內研究綜述[J]. 船舶力學, 2014,18(11): 1397-1414.

WANG Zheng, HONG Ming, LIU Cheng. Domestic review of the submerged structure vibration and acoustic radiation characteristics based on FEM/BEM [J]. Journal of Ship Mechanics， 2014,18(11): 1397-1414.

[11] 武大江，梅志遠，王永歷. 充水密加筋夾層結構固有特性仿真及試驗研究[J]. 振動與沖擊, 2016,35(15): 134-139.

WU Dajiang, MEI Zhiyuan, WANG Yongli. Nature characteristics simulation and tests for water-filled multi-stiffened sandwich structures[J].Journal of Vibration and Shock,2016,35 (15):134-139.

[12] 吳健，李澤成，熊晨熙. 基于Abaqus的水下結構聲輻射仿真方法[J]. 計算機輔助工程, 2015,24(6): 37-41.

WU Jian, LI Zecheng, XIONG Chenxi. Simulation method of sound radiation of underwater structure based on Abaqus [J]. Computer Aided Engineering， 2015,24(6): 37-41.

[13] LIU Ruijun, HAO Zhiyong, XU Wang, et al. A study of the influence of cooling water on the structural modes and vibro-acoustic characteristics of a gasoline engine[J]. Applied Acoustics, 2016, 104(1): 42-49.

[14] 陳冬冬，王輝，楊景玲，等. 油底殼流固耦合動力學特性分析[J]. 噪聲與振動控制， 2014,34(6): 17-19.

CHEN Dongdong, WANG Hui, YANG Jingling, et al. Fluid-structure coupled model for modal analysis of an oil pan [J]. Noise and Vibration Control, 2014,34(6): 17-19.

[15] 馮威，袁兆成，劉偉哲. 用液固耦合方法研究柴油機油底殼輻射聲場[J]. 內燃機學報, 2005,23(6): 536-540.

FENG Wei, YUAN Zhaocheng, LIU Weizhe. Study on radiated acoustic field of oil pan by liquid-solid coupled [J]. Transactions of CSICE, 2005,23(6): 536-540.

[16] 王勖成. 有限單元法[M]. 北京: 清華大學出版社, 2003.

[17] CLOUGH R W, PENZIEN J, GRIFFIN D S. Dynamics of structures[M]. [S.l.] ： Wiley, 2010.

[18] 程耀東. 機械振動學[M]. 杭州: 浙江大學出版社, 1988.

[19] 張永恒. 工程優化設計與MATLAB實現[M]. 北京: 清華大學出版社, 2011.

[20] 華東師范大學數學系. 數學分析[M]. 北京: 高等教育出版社, 2010.

[21] 張亮，袁兆成，黃震. 流固耦合有限元法用于油底殼模態計算[J]. 振動與沖擊, 2003,22(4): 102-103.

ZHANG Liang, YUAN Zhaocheng, HUANG Zhen. Fluid-structure coupled finite element method applied in oil pan’s mode calculation [J]. Journal of Vibration and Shock, 2003,22(4): 102-103.

Theapplicationofanimprovedwetmodemethodinfluid-structureinteraction

LIURuijun,HAOZhiyong,ZHENGXu,TANJianglin

(CollegeofEnergyEngineering,ZhejiangUniversity,Hangzhou310027,China)

The singularity of the fluid stiffness matrix in the equations of motion was pointed out, which made the existing wet mode method unavailable. Meanwhile, the contradiction of the method isolating the zero-frequency item was indicated. The paper shows that the root of the problem of the wet mode method is the unreasonable presumption. The presumption simultaneously neglects the compressibility of the fluid as well as the influence of the free surface fluctuation which aims at the easier computation. Two solutions called the direct method and the fixed point method were put forward based on the above conclusion. The direct method is more suitable for the computation with a small fluid domain scale while the fixed point method is fit for a large one. In this paper, the structural characteristics of an oil pan with different oil mass were calculated by a Matlab program based on the fixed point method. The comparison demonstrates that the structural modal frequencies decrease firstly, then increase and finally become stable with the oil mass increasing from 0. The deformation magnitude of the modal shapes decrease considerably when the fluid is added. For the same order of mode, the wet modal shapes differ a lot from the dry modal shapes with less fluid addition except the 1st mode. However, the wet modal shapes tend to be stable and the same as the dry modal shapes with the continuous increase of oil mass.

fluid-structure interaction; wet mode; direct method; fixed point method

2016-05-17 修改稿收到日期： 2016-09-18

劉瑞駿 男，博士生，1990年生

郝志勇 男，教授，博士生導師，1955年生

TB122

A

10.13465/j.cnki.jvs.2017.22.031