壓電智能結構振動的一致性PID(CPID)控制

白 亮， 馮蘊雯， 薛小鋒

(西北工業大學 航空學院，西安 710072)

壓電智能結構振動的一致性PID(CPID)控制

白 亮， 馮蘊雯， 薛小鋒

(西北工業大學 航空學院，西安 710072)

將一致性控制方法和PID控制方法的基本思想相結合，提出了一種適用于壓電智能結構振動控制的一致性PID(Consensus-PID，CPID)控制方法。該方法將系統輸出偏差作為PID控制器的輸入，PID控制器的輸出及其在采樣周期內的變化量作為一致性控制器的輸入，致動器的輸入電壓為一致性控制器的輸出。推導壓電智能結構振動控制方程，以兩邊簡支的壓電智能梁為數值算例，建立動力學有限元模型，數值結果表明 CPID控制方法能夠有效控制壓電智能結構的振動，當某些傳感器失效時，對比集中式PID控制，系統在CPID控制下仍然能保持較好的控制效果。

一致性控制；PID控制；壓電智能結構；振動控制

一致性控制方法在分布式參數系統中有著廣泛的應用，Demetriou[1]提出了一種基于自適應一致性控制的過濾器設計方法，并將其應用于由多個傳感器組成的分布式參數系統中；Motee等[2]將一致性控制方法應用于空間分布式參數系統結構的優化控制；Mu等[3]應用一致性控制方法設計了兩種過濾器，并將其應用于空間分布式參數系統的狀態評估。壓電材料作為致動器、傳感器粘貼在柔性結構表面或嵌入于柔性結構內部，成為壓電智能結構[4]，壓電智能結構是一類分布式參數系統[5]，廣泛應用于柔性結構振動控制領域[6-7]。

近年來，國內外學者對壓電智能結構振動控制中常用的PID(Proportional Integrative Derivative)控制方法進行了較為深入的研究。其中，Jaensch等[8]將高增益PID位移反饋控制器用于控制系統中，研究了新方法的控制效果和控制穩定性。Li等[9]將一種改進的PID控制方法應用于飛行器氣動噪聲的抑制。Zhang等[10]針對薄墻智能結構提出了一種改進的PID控制法。另外，其它主動控制方法也被用于壓電智能結構的振動控制，如PPF(Positive Position Feedback)控制[11]，自適應控制[12]，基于模糊邏輯的控制方法[13]等。而上述方法都是集中式控制，在集中式控制中，一個特定的控制器以固定形式或自適應動態形式存在，集中式控制器計算出全部致動器所需的輸入信號，所有的致動器和傳感器直接與控制器連接。對于由多組離散分布的致動器/傳感器粘貼在柔性結構表面所組成的壓電智能結構，在集中式控制下若某一傳感器失效或誤讀，與其同組的致動器無法輸出控制力或輸出錯誤控制力，這會對系統的振動控制產生不利影響。解決辦法是用分散式控制代替集中式控制，將集中式控制器替換成若干個分散的、有一定相對獨立性的子控制器，每個子控制器和一組致動器/傳感器組成一個子控制系統，將一致性控制的基本思想應用于分散式控制系統中，根據一致性協議將若干個子控制系統組成網絡，使得各個子控制器的輸出信號可以相互傳遞，若某一個子控制系統的傳感器失效或誤讀，其它正常工作的子控制系統會將其控制器的輸出信號傳遞給無法正常工作的子控制系統，使其致動器工作。圖1對比了集中式控制、一致性控制的不同之處。

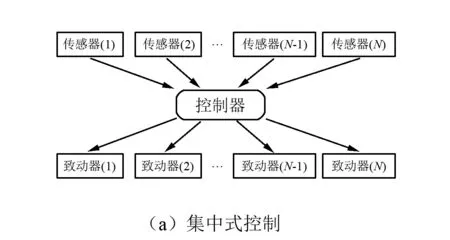
Sahasrabudhe等[14]已經提出可以將一致性控制用于壓電智能結構的振動控制，并建立了一致性控制系統框架，但是并沒有給出具體的控制方法和建模過程。為了克服上述集中式控制的局限性，將一致性控制方法和PID控制方法的基本思想相結合，提出了一種適用于壓電智能結構振動控制的一致性PID(Consensus-PID,CPID)控制方法，以系統輸出偏差作為PID控制器的輸入，以PID控制器的輸出及其在采樣周期內的變化量作為一致性控制器的輸入，以一致性控制器的輸出作為致動器的輸入電壓，實現對壓電智能結構的振動控制。由線彈性壓電智能結構有限元方程推導系統振動控制方程。用ANSYS參數化語言編寫了壓電智能結構振動控制分析的有限元程序，數值仿真結果證明了CPID控制方法能夠有效控制壓電智能結構的振動，當某些傳感器失效時，對比于集中式PID控制，系統在CPID控制下仍然能保持較好的控制效果。

1 壓電智能結構的CPID控制方法

在實際應用中，傳感器通常只能獲得各采樣時刻的測量值，因此系統輸出偏差是不連續的。設采樣周期為T，將離散的采樣時刻用總的工作時間表示為

t=k×T(k=0,1,2,…)

(1)

式中，k為采樣序號。

壓電智能結構CPID控制系統中有N個傳感器、N個PID控制器和N個致動器，如圖2所示。Fu為作用在壓電智能結構上的外部干擾力載荷；Fa為致動器產生的反饋控制力；ri(k)為第k次采樣時傳感器(i)的期望輸出電壓；φi(k)為第k次采樣時傳感器(i)的實際輸出電壓；xi(k)、vi(k)分別為第k次采樣時經過PID控制器(i)放大后的輸出電壓及其在采樣周期內的變化量；Xi(k)和Vi(k)分別為經過一致性控制后的xi(k)和vi(k)；Xi(k)同時也為致動器(i)的輸入電壓，其中i=1,2,…,N，k=0,1,2,…。

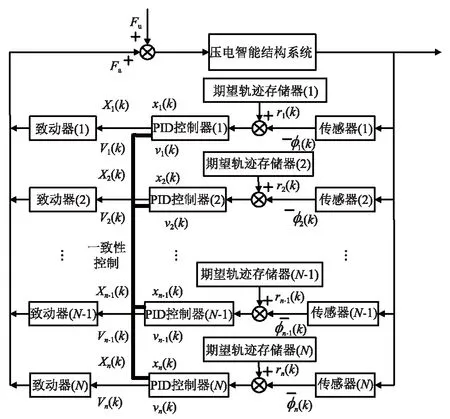
圖2 壓電智能結構CPID控制原理框圖Fig.2 The CPID control block diagram of piezoelectric smart structures

以傳感器輸出電壓為反饋信號，定義傳感器(i)所在位置的輸出偏差為

ei(k)=0-φi(k) (i=1,2,…,N)

(2)

式中：φi(k)為第k次采樣時傳感器(i)的實際輸出電壓。

對于時間離散的系統，經過PID控制器(i)放大后的輸出電壓可以近似表示為

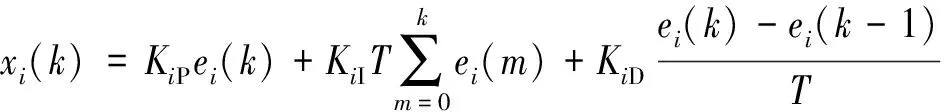
(3)

式中：KiP、KiI、KiD分別為PID控制器(i)的比例、積分、微分系數；T為采樣周期。

二階系統一致性與一階系統一致性的區別在于二階系統要同時考慮位置和速度，根據一致性協議通過控制智能體的加速度來控制速度，通過速度的變化以達到間接控制位置的目的。應用二階系統一致性控制方法，系統中要達到一致性的變量有兩個，即PID控制器的輸出電壓xi(k)及其在采樣周期內的變化量vi(k)。第k次采樣時，PID控制器(i)輸出電壓在采樣周期內的變化量為

vi(k)=xi(k+1)-xi(k)
(k=0,1,2,…;i=1,2,…,N)

(4)

二階系統一致性協議[15]表示為

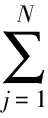
(5)

式中：lij為通信拓撲圖的拉普拉斯矩陣L中的元素；k1、k2為比例參數，其數值的選取要滿足振動控制系統的穩定性條件。

L=D-A

(6)

式中：D為通信拓撲圖的入度矩陣；A為通信拓撲圖的鄰接矩陣。

假設：一致性控制在一個采樣周期內進行，且vi(k)經過一個采樣周期的一致性控制后仍然用于第k次采樣的計算

Vi(k)=vi(k)+μi(k) (k=0,1,2,…；i=1,2,…,N)

(7)

經過一致性控制后，致動器(i)的輸入電壓可以表示為

Xi(k+1)=xi(k)+Vi(k) (k=0,1,2,…；i=1,2,…,N)

(8)

將式(4)、式(5)、式(7)代入式(8)整理后可得

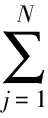
(9)

當傳感器(i)因為失效而無法輸出信號時，式(9)可以表示為

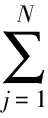
(10)

由式(10)可知，當傳感器(i)失效時，通過一致性協議，正常工作的PID控制器的輸出信號會傳遞給致動器(i)，使其工作。

2 壓電智能結構振動的CPID控制方程

考慮結構阻尼，壓電智能結構全局有限元動力方程[16]為

(11)

式中：ui、φi分別為整體坐標系下節點的位移和電壓；Muu、Cuu、Kuu、Kuφ(Kφu)、Kφφ分別為結構整體質量、阻尼、剛度、力電耦合剛度、介電剛度矩陣；Fu和Fφ分別為整體坐標系下的力荷載向量和電荷載向量。

將式(11)中的第二個方程代入式(11)的第一個方程中，可得用節點位移形式表示的壓電智能結構有限元動力方程

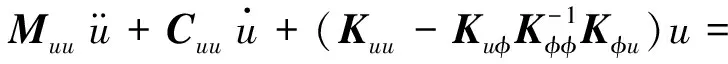
(12)

致動器的輸入電壓與電荷載之間的關系為

Fφ=GaXi(k)

(13)

式中，Ga為反饋控制增益。

將式 (9)、式(13)代入式(12)可得，在傳感器(i)正常工作時，用節點位移表示壓電智能結構振動的CPID控制方程為

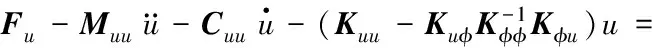
(14)

將式(10)、式(13)代入式(12)可得，在傳感器(i)因為失效而無法輸出信號時，用節點位移表示壓電智能結構振動的CPID控制方程為

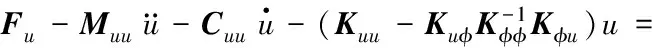
(15)

3 算 例

壓電智能梁由一個簡支梁和對稱粘貼在簡支梁上下表面的四組致動器/傳感器組成，致動器/傳感器位置參數如圖3所示。簡支梁幾何參數為：576 mm×25.4 mm×0.8 mm；致動器/傳感器幾何參數為：72 mm×25.4 mm×0.61 mm，致動器和傳感器的材料為PZT-5H，簡支梁結構為鋁質材料，材料屬性見表1，Fu=0.1 N為作用在壓電智能梁結構中點P的瞬時荷載，從圖3可知，同組的致動器(i)/傳感器(i)和PID控制器(i)連接，其中i=1,2,3,4，為了計算結果與集中式PID控制的計算結果相比較，四個PID控制器的比例、積分、微分系數相同，比例系數KP=12.5、微分系數KI=0.02、積分系數KD=0.001。PID控制器(i)輸出信號根據通信拓撲圖進行傳遞，如圖4所示。

假設致動器/傳感器與簡支梁之間為理想粘貼，不發生相對剪切運動，傳感器(3)不會失效。用SOLID45單元模擬金屬鋁材料，SOLID5單元模擬壓電材料PZT-5H，將每個致動器/傳感器劃分為：8×8×1個單元，簡支梁劃分為：64×8×1個單元，用命令CP分別耦合致動器和傳感器上下表面節點的電自由度，與簡支梁相粘貼的致動器下表面和傳感器上表面電學邊界條件定義為0 V。系統的瑞利阻尼系數很小為：α=β=0.000 5。傳感器信號的采樣周期[17]為：T=1/(20fh)，其中fh為壓電智能梁的一階無阻尼自振頻率。

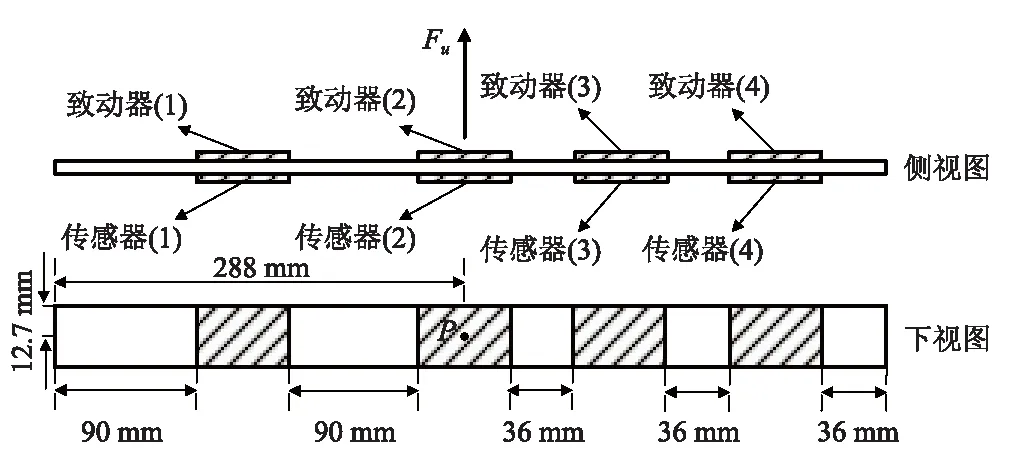
圖3 壓電智能梁示意圖Fig.3 Schematic of the piezoelectric smart beam

表1 壓電智能梁材料屬性

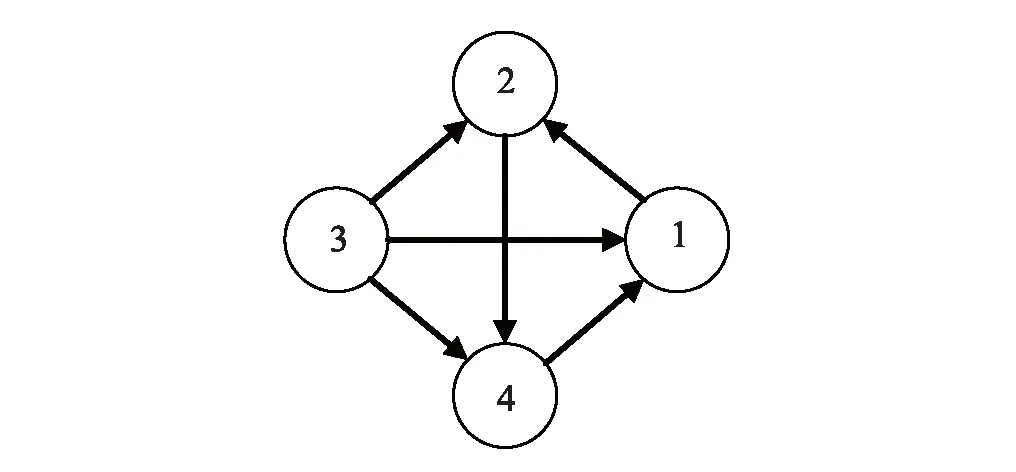
圖4 通信拓撲圖Fig. 4 Schematic of communication topology

取式(5)中的比例參數：k1=0.3，k2=0.5。對算例進行數值計算之前要驗證所選取的比例參數滿足系統穩定的條件。不考慮結構阻尼時，在壓電智能梁結構中點P設定一個初始位移，然后令其自由振動，點P位移響應如圖5(a)所示。為了便于觀察振動收斂情況，取0.777 906～9.988 764 s的位移響應，如圖5(b)所示。可知此時系統是不穩定的，這是因為在信號傳遞的過程中，可能會使某些致動器的輸入電壓過大，致動器產生較大的控制力，這個控制力的一部分用于結構振動控制，額外的部分可能產生新的外部擾動。結構阻尼達到一定值時，即使存在這個新的外部擾動，系統仍然可以保持穩定。當結構阻尼系數α=β=0.000 087時，點P位移響應如圖5(c)所示。取0.777 906～9.988 764 s的位移響應，如圖5(d)所示。可知此時系統是穩定的。因為算例中結構的瑞利阻尼系數α=β=0.000 5gt;0.000 087，所以比例參數取k1=0.3，k2=0.5時該系統穩定。

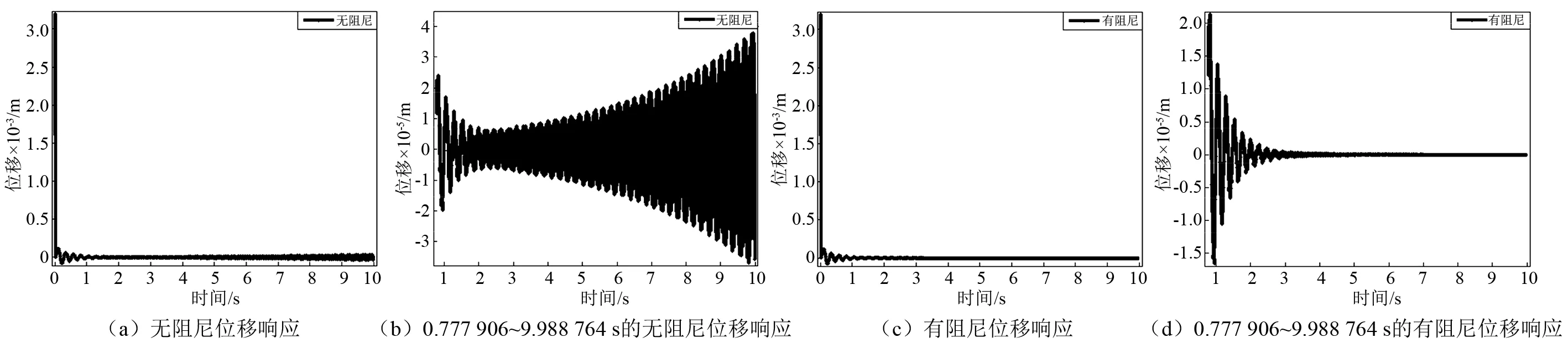
圖5 點P位移響應Fig.5 Displacement response of the point P

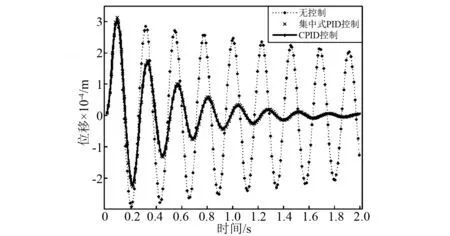
傳感器都正常工作時，系統在瞬時荷載Fu作用下，點P位移響應，如圖6(a)所示。四個致動器輸入電壓的變化范圍，如圖6(b)所示。由圖6(a)可知，對比于集中式PID控制，系統在CPID控制下的收斂速度較快。由圖6(b)可知，在集中式PID控制下，致動器(2)的輸入電壓最大(最大輸入電壓為134.063 V，最小輸入電壓為-80.154 V)且大于在CPID控制下致動器(2)的輸入電壓，而致動器(1)和致動器(4)的輸入電壓較小且小于在CPID控制下致動器(1)和致動器(4)的輸入電壓，說明致動器(2)在集中式PID控制下產生的控制力較大，但是致動器(1)和致動器(4)在集中式PID控制下產生的控制力較小。集中式PID控制下，致動器(2)是在一種滿狀態或超負荷狀態下工作，而致動器(1)和致動器(4)并沒有滿狀態工作，沒有充分發揮自身的作用。系統在CPID控制下所有致動器輸入電壓均較大，說明各個致動器均可以產生較大的控制力，而且可以避免某些致動器在滿狀態或超負荷狀態下工作，在CPID控制下系統可以將電能更合理的分配給每個致動器，各個致動器之間通過相互協作共同完成任務，而不是僅依靠某些致動器的滿狀態或超負荷工作完成任務。

圖7(a)～圖7(c)為壓電智能梁結構中點P在瞬時荷載作用下，傳感器(1)、傳感器(2)、傳感器(4)分別失效時，點P位移響應，圖7(d)～圖7(f)為傳感器(1)和傳感器(2)、傳感器(1)和傳感器(4)、傳感器(2)和傳感器(4)分別失效時，點P位移響應。對比于集中式PID控制，當某些傳感器失效時，系統在CPID控制下的收斂速度較快。用對數衰減公式計算系統的阻尼比ξ，計算結果如圖8所示。對比于集中式PID控制，在CPID控制下系統的阻尼比ξ較大。以全部傳感器正常工作時，集中式PID控制下系統的阻尼比為參照值，對比不同條件下系統的阻尼比可知：當傳感器(2)失效時，在集中式PID控制下，系統的阻尼比大幅下降僅為參照值的58.2%，在某些關鍵位置的傳感器失效時，系統的振動控制效果大幅降低，在CPID控制下，系統的阻尼比可達到參照值的82.8%，控制效果有較大幅度的提升；當有一個傳感器失效時，系統在CPID控制下，平均實現參照值88.2%的控制效果，與集中式PID控制下78.4%的控制效果相比，有較大的提升，當有兩個傳感器失效時，系統在CPID控制下，平均實現參照值76.5%的控制效果，與集中式PID控制下57.7%的控制效果相比，有大幅的提升，說明傳感器失效的越多，對比集中式PID控制，CPID控制方法的控制效果越好。

圖9列出系統在不同方法控制下和不同工作條件下，所有致動器中的最大輸入電壓Vmax和最小輸入電壓Vmin，對比于集中式PID控制，系統在CPID控制下所有致動器中的最大輸入電壓Vmax較小且最小輸入電壓Vmin較大，在振動控制過程中，若輸入電壓過大則致動器可能被擊穿，說明在CPID控制下系統可以將電能更合理的分配給各個致動器，避免某些致動器輸入電壓過大，在有效控制壓電智能梁振動的同時對致動器起到了一定的保護作用。

(a) 點P位移響應

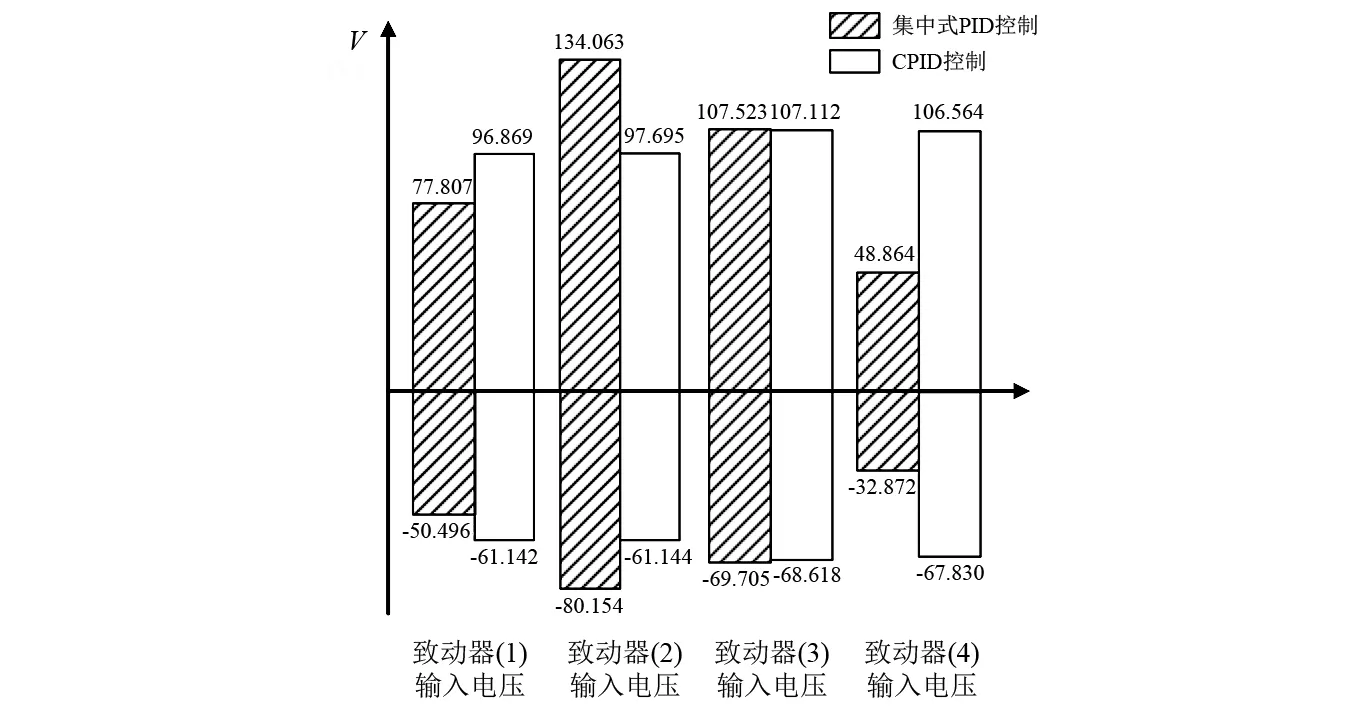
(b) 致動器輸入電壓

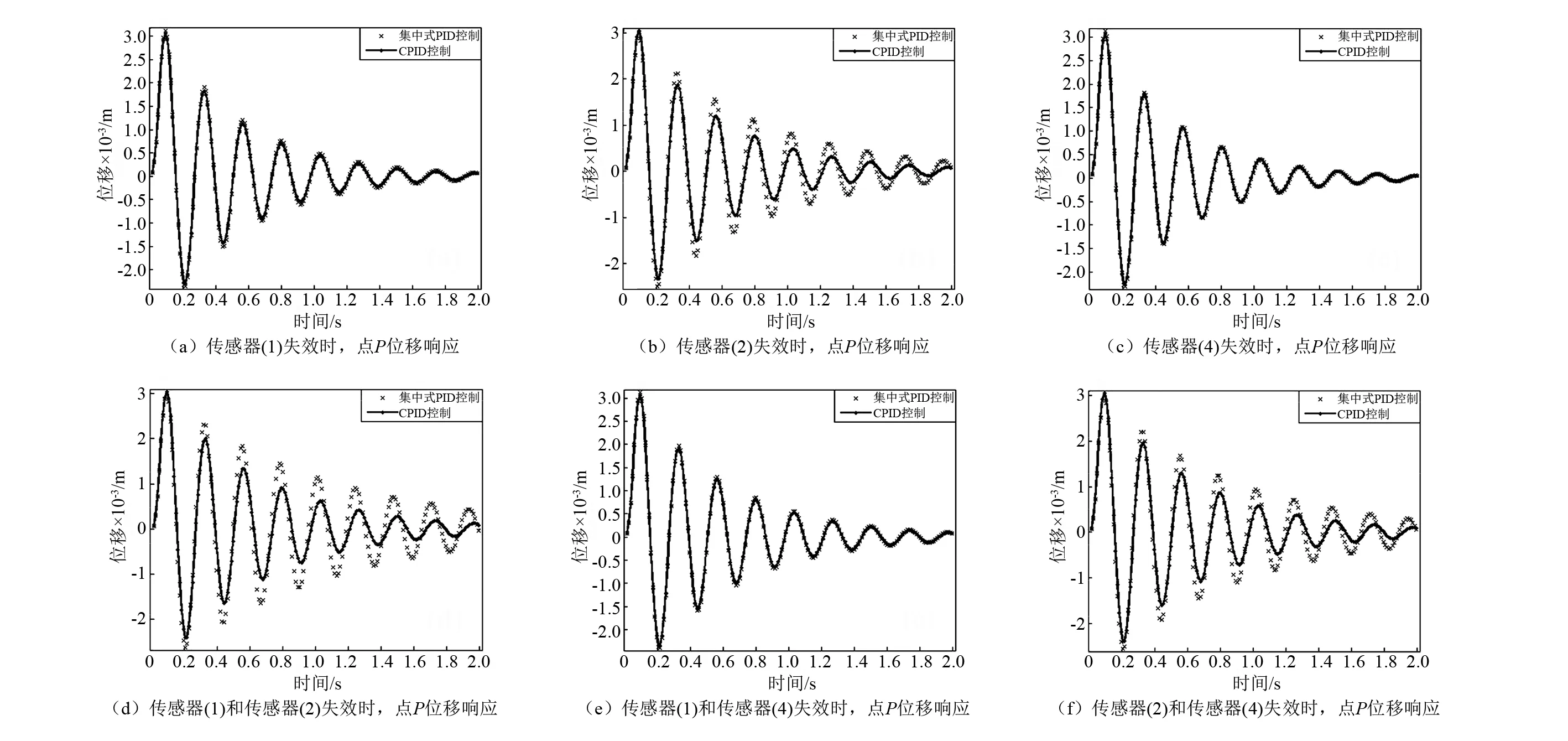
圖7 一個或兩個傳感器失效時點P位移響應Fig.7 Displacement response of the point P

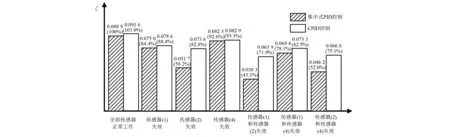
圖8 系統的阻尼比Fig.8 System damping ratio

表2列出不同工作條件下，系統阻尼頻率ωd的計算結果，與系統一階無阻尼自振頻率4.435 Hz相比，在集中式PID控制和CPID控制下系統的阻尼頻率都有不同程度的降低，通過與圖8所示系統的阻尼比計算結果相對比，系統的阻尼比ξ越大，系統阻尼頻率ωd越小。

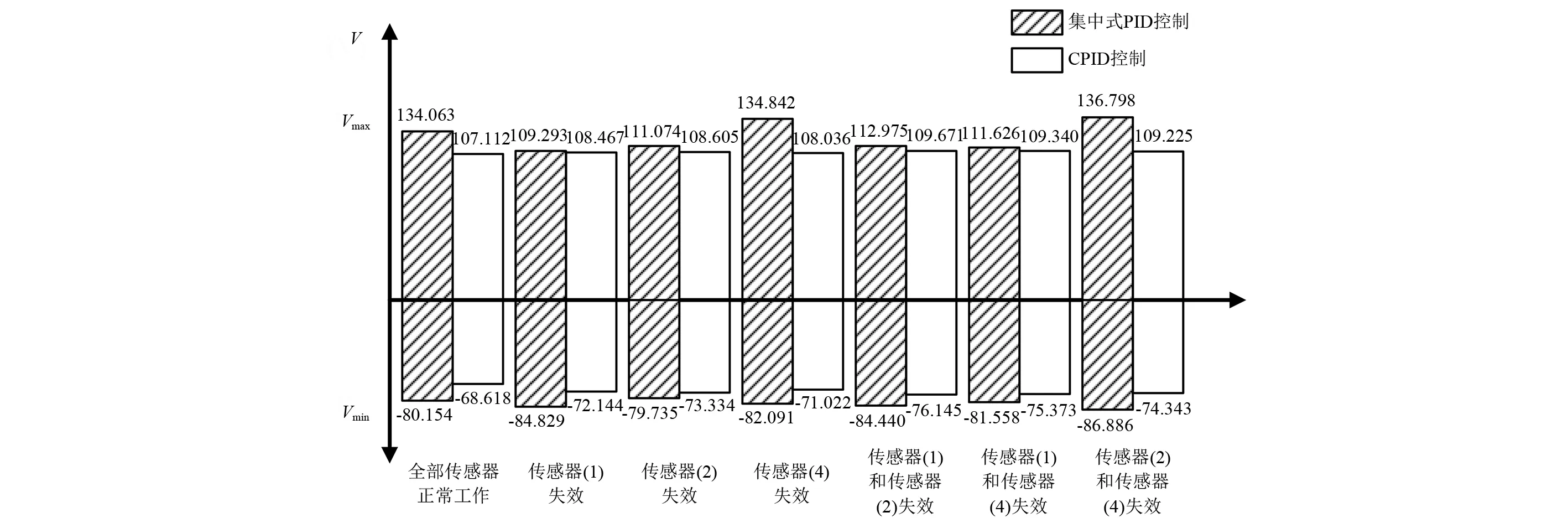
圖9 所有致動器中的最大輸入電壓和最小輸入電壓Fig.9 The maximum input voltage and the minimum input voltage of all the actuators

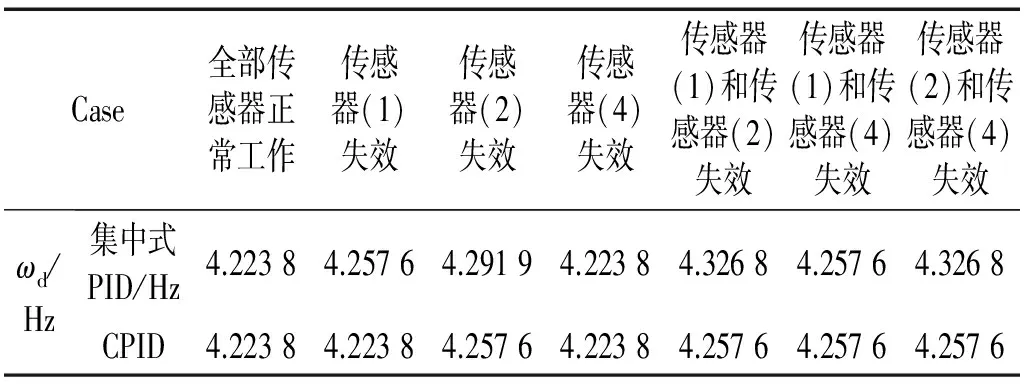
表2 系統的阻尼頻率

為了進一步驗證CPID控制方法對壓電智能結構振動控制的有效性，考慮全部傳感器正常工作的條件下，在壓電智能梁結構中點P分別施加簡諧荷載和隨機荷載，對系統強迫振動進行數值仿真，其中簡諧荷載函數為：f(t)=0.1 cos(9πt)。圖10(a)為壓電智能梁在簡諧荷載作用下，點P的位移響應，無控制時點P位移響應的均方根值為3.17×10-3，在CPID控制下位移響應的均方根值為0.82×10-3，可知在CPID控制下點P的位移響應降低了74.1%，圖10(b)為壓電智能梁在隨機荷載作用下，點P的位移響應，無控制時點P位移響應的均方根值為0.65×10-3，在CPID控制下點P位移響應的均方根值為0.29×10-3，可知在CPID控制下點P的位移響應降低了55.4%。通過比較發現CPID控制對簡諧荷載和隨機荷載下壓電智能結構的振動控制效果顯著。

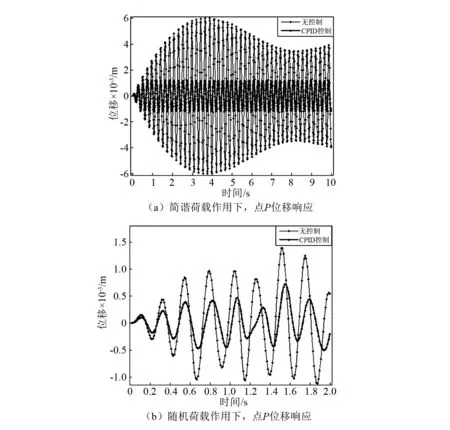
圖10 簡諧荷載和隨機荷載作用下點P位移響應Fig.10 Displacement responseof the point P under a harmonic and random force excitations

4 結 論

將一致性控制方法與PID控制方法的基本思想相結合，提出了一種適用于壓電智能結構振動控制的一致性PID(Consensus-PID,CPID)控制方法。用ANSYS參數化語言編寫了壓電智能結構振動控制分析的有限元程序，進行數值仿真。研究結果表明：

(1)CPID控制方法對壓電智能結構的振動控制是有效的，提高了集中式PID控制的收斂速度。

(2)當壓電智能結構中某些傳感器失效時，對比于集中式PID控制，系統在CPID控制下仍然能保持較好的控制效果，失效的傳感器越多，CPID控制方法的優勢越明顯。

(3)對比于集中式PID控制，系統在CPID控制下致動器的最大輸入電壓Vmax較小且最小輸入電壓Vmin較大，對致動器起到了一定的保護作用。

[ 1 ] DEMETRIOU M A. Design of consensus and adaptive consensus filtersfor distributed parameter systems[J]. Automatica, 2010, 46(2): 300-311.

[ 2 ] MOTEE N, JADBBAIE A. Optimal control of spatially distributed systems [J]. IEEE Transactions on Automatic Control, 2008, 53(7): 1616-1629.

[ 3 ] MU Wenying, CUI Baotong, LI Wen, et al. Improving control and estimation for distributed parameter systems utilizing mobile actuator-sensor network [J]. ISA Transactions, 2014, 53(4): 1087-1095.

[ 4 ] ZABILHOLLAH A, SEDAGAHTI R, GANESAN R. Active vibration suppression of smart laminated beams using layerwise theory and an optional control strategy [J]. Smart Materials and Structures, 2007,16(6): 2190-2201.

[ 5 ] BAUDRY M, MICHEAU P, BERRY A. Decentralized harmonic active vibration control of a flexible plate using piezoelectric actuator-sensor pairs [J]. The Journal of the Acoustical Society of America, 2006, 119(1): 262-277.

[ 6 ] CHOI S B, SEONG M S, HA S H. Accurate position control of a flexible arm using a piezoactuator associated with a hysteresis compensator [J]. Smart Materials and Structures, 2013, 22(4): 1-13.

[ 7 ] SPRUCE C J, TURNER J K. Tower vibration control of active stall wind turbine [J]. IEEE Transactions on Control Systems Technology, 2013, 21(4): 1049-1066.

[ 8 ] JAENSCH M, LAMPERTH M U. Investigations into the stability of a PID-controlled micropositioning and vibration attenuation system [J].Smart Materials and Structures, 2007, 16(4): 1066-1075.

[ 9 ] LI Yunlong, WANG Xiaojun, HUANG Ren, et al. Active vibration and noise control of vibro-acoustic system by using PID controller [J]. Journal of Sound and Vibration, 2015, 348: 57-70.

[10] ZHANG Shunqi, RUDIGER S, QIN Xiansheng. Active vibration control of piezoelectric bonded smart structures using PID algorithm [J]. Chinese Journal of Aeronautics, 2015, 28(1): 305-313.

[11] GRASSO E, TOTARO N, JANOCHA H. Piezoelectric self sensing actuators for high voltage excitation [J]. Smart Materials and Structures, 2013, 22(6): 06518.

[12] YANG S M, SHEU G J, LI C C. Synthesis of reference signal in adaptive feedback controller for structure vibration suppression [J]. Journal Intelligent Material Systems and Structures, 2008, 19:727-734.

[13] MAKIHARA K, KUROISHI C, FUKUNAGA H. Adaptive multimodal vibration suppression using fuzzy-based control with limited structural data [J]. Smart Materials and Structures, 2013, 22(7): 075031.

[14] SAHASRABUDHE V, MEHRA A. A multi-agent control system framework for smart structures [C]∥Navigation, and Control Conference and Exhibit. Boston :AIAA,1998: 4202-4215.

[15] XIE Dongmei, WANG Shaokun. Consensus of second-order discrete-time multi-agent systems with fixed topology [J]. Journal of Mathematical Analysis and Applications, 2012, 387(4): 8-16.

[16] GUENNAM A E, LUCCIONI B M. Piezoelectric shell FE for the static and dynamic analysis of piezoelectric fiber composite laminates [J]. Smart Material and Structures, 2009, 18(9): 095044.

[17] KARAGULLE H, MALGACE L, OKTEM H F. Analysis of active vibration control in smart structures by ANSYS[J]. Smart Material and Structures, 2004,13(4): 661-667.

AconsensusPID(CPID)controlalgorithmforvibrationcontrolofpiezoelectricsmartstructures

BAILiang，FENGYunwen，XUEXiaofeng

(SchoolofAeronautics，NorthwesternPolytechnicalUniversity，Xi’an710072，China)

By combining the idea of PID control and the consensus control algorithm, a new consensus-PID (CPID) control algorithm was proposed, which was used for vibration control of piezoelectric smart structures. In this new approach, the inputs of PID controllers were the system output errors. The outputs of PID controllers and their variations in the sampling period were treated as the inputs of the consensus controller. The input voltages of each actuator were the outputs of the consensus controller. The vibration control equations of piezoelectric smart structures were derived from the finite element dynamic equations of a linear elastic piezoelectric smart structure. The CPID control algorithm was numerically investigated for the smart structure, i.e., a piezoelectric smart beam that was simply supported at its both sides. The finite element model of a piezoelectric smart beam for vibration control was established by ANSYS. Numerical results demonstrate that the CPID control law can successfully control the vibration of the piezoelectric smart structure. Comparing with the centralized PID control algorithm, the new CPID control approach can maintain higher performance for vibration control in the system of piezoelectric smart structures, even though some sensors fail.

consensus control; proportional integrative derivative control; piezoelectric smart structure; vibration control

國家自然科學基金資助(10577015)

2016-04-18 修改稿收到日期： 2016-09-09

白亮 男，博士生，1987年生

馮蘊雯 女，博士，教授，1968年生

TB535

A

10.13465/j.cnki.jvs.2017.22.030