阻尼材料模量與損耗因子的雙邊梁測量反演誤差機理與控制
屈忠鵬, 盛美萍
(西北工業(yè)大學 航海學院,西安 710072)
阻尼材料模量與損耗因子的雙邊梁測量反演誤差機理與控制
屈忠鵬, 盛美萍
(西北工業(yè)大學 航海學院,西安 710072)
通過引入中間變量,得到了雙邊自由阻尼梁阻尼層楊氏模量和損耗因子的簡化反演公式,并在此基礎上進行誤差分析,給出了高階誤差預測公式。研究表明,影響反演精度的重要參數(shù)為復合梁與基底梁的剛度比;剛度比越大,反演精度越高;當剛度比接近于1時,共振頻率比和質量比的誤差放大倍數(shù)急劇增加,導致反演誤差變大;通過增大阻尼層與基底層的厚度比和模量比,可以增大剛度比,進而提高反演精度。仿真分析驗證了該結論的正確性。
阻尼材料; 彎曲共振法; 雙邊梁; 誤差分析; 剛度比
阻尼技術可以在較寬頻帶內對振動噪聲進行有效控制,是減振降噪的一個重要手段,因此阻尼材料廣泛應用于船艇、飛行器、汽車和建筑降噪等諸多領域[1-2]。阻尼材料的重要特性參數(shù)為模量和損耗因子,其獲取主要依賴于試驗測量[3-5]。
彎曲共振法是阻尼測量的常用方法之一,具有試驗架構簡單、測量頻帶寬等優(yōu)點。但是,因為需要根據(jù)基底梁與復合梁的特性差別對模量和損耗因子進行反演[6-7],所以其計算結果對測量誤差較為敏感。為有效控制誤差和指導試件設計,工程人員需清楚了解誤差傳遞的特征。通過引入誤差放大因子的概念,朱蓓麗等[8-9]對夾心梁結構、胡衛(wèi)強等[10-11]對單邊和雙邊自由阻尼梁結構分別進行了研究,得到試件設計的若干指導意見。但由于反演公式復雜,作者們借助符號運算進行分析,或僅進行了部分推導,無法得到誤差放大因子的解析表達式,因此難以清晰揭示誤差傳遞的本質。
本文針對雙邊自由阻尼梁結構開展研究。通過引入中間變量,對復雜的反演公式進行了化簡,從而避免了符號運算,得到誤差放大因子的解析表達式,并進一步給出了更準確的高階誤差預測公式。在此基礎上,提出改善測量精度的途徑,并通過仿真分析進行了驗證。
1 理論基礎
對于雙邊自由阻尼復合梁(見圖1),阻尼層楊氏模量和損耗因子反演公式為
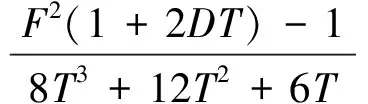
(1)
(2)
式中:E1為基底層楊氏模量;ηc為復合梁損耗因子;F為復合梁與基底梁的共振頻率比;D和T分別為阻尼層與基底層的密度比和厚度比。實際測量中,D通過復合梁和基底梁的質量比S獲得,其關系為
D=(S-1)/(2T)
(3)
復合梁與基底梁的剛度比為
ε=F2S
(4)
并記厚度比參量
τ=8T3+12T2+6T
(5)
將式(3)~式(5)代入式(1)和式(2),整理可得
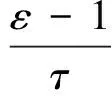
(6)
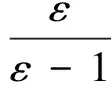
(7)
整理后公式形式簡潔,便于進行誤差分析。

圖1 雙邊自由阻尼梁Fig.1 The symmetric free-layer beam
2 誤差分析
根據(jù)誤差放大因子定義,阻尼層楊氏模量和損耗因子的誤差可表示為
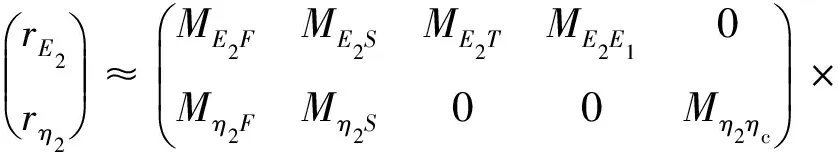
(8)
(9)
(10)
式(9)和式(10)分別為與楊氏模量E2和損耗因子η2相關的誤差放大因子。其中ME2E1和Mη2ηc的值為1, 這表示E1和ηc的誤差會等量傳遞給E2和η2。ME2T的值與厚度比T有關, 介于-3~-1,這表示T的誤差會被放大1~3倍,但方向相反。ME2F、ME2S、Mη2F和Mη2S的值僅由剛度比ε決定, 并且F的誤差放大倍數(shù)為S的2倍。將式(6)變形可得剛度比為
ε=(8T3+12T2+6T)e+1
(11)
式中:e=E2/E1為阻尼層與基底層的模量比。 一般而言,e?1, 可見剛度比ε略大于1。
各誤差放大因子隨ε變化的曲線,如圖2所示。 當剛度比較小時,F(xiàn)與S的誤差放大因子明顯高于其它值, 這使得F和S的誤差被放大數(shù)十倍甚至上百倍,將會導致阻尼層楊氏模量和損耗因子的反演精度急劇降低。隨著剛度比ε增大,F(xiàn)與S的誤差放大因子減小, 當εgt;1.2時, 其值降至與其它放大因子相同的量級。
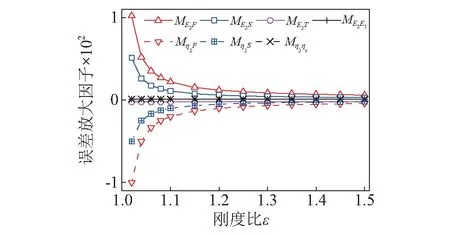
圖2 誤差放大因子比較Fig.2 Comparison of the error magnification factors
由上述分析可知,提高剛度比ε可有效控制反演誤差。 由式(11)可見提高ε有兩個途徑: 增加厚度比T和模量比e。厚度比T可通過增加阻尼層厚度或減小基底層厚度而增加,模量比可通過更換較軟基底層而增加。而當ε較小時, 頻率比F和質量比S的誤差應受到嚴格控制。
誤差放大因子根據(jù)一階泰勒展開獲得,用于分析誤差傳遞特性是足夠的。若是要更精確地預測誤差,則需進行高階計算。對式(6)和式(7)進行完整泰勒展開可得
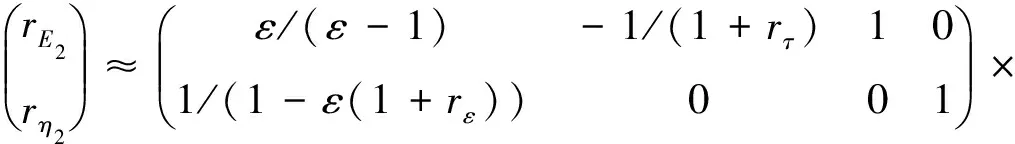
(12)
其中rε和rτ為中間變量的相對誤差,可通過式(4)和式(5)求得
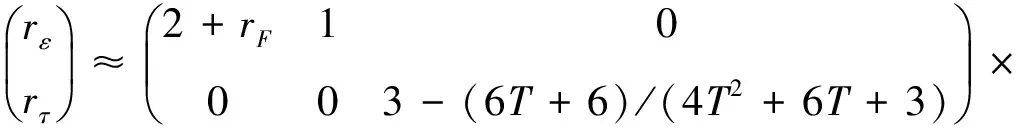
(13)
3 仿真驗證
阻尼材料的特性參數(shù)一般隨頻率有所變化。這里將楊氏模量和損耗因子均設為常值,這不影響結果的驗證,但可簡化分析和討論過程。假定某阻尼材料的楊氏模量為100 MPa,損耗因子為0.4,其厚度為1 mm。選擇三個試件進行分析,試件1選用鋼材料為基底層,厚度為1 mm;試件2減小基底層的厚度為0.5 mm;試件3將基底選為有機玻璃,厚度為1 mm。試件長度均為200 mm。阻尼材料、鋼和有機玻璃的密度分別為1 200 kg/m3、7 800 kg/m3和1 200 kg/m3,鋼和有機玻璃的模量分別為200 GPa和5 GPa。三個試件復合梁與基底梁的剛度比由小變大,依次為1.01、1.06和1.52。
仿真得到的頻響曲線,如圖3所示。從其中可識別得到共振頻率比F和復合梁的損耗因子ηc。將頻率比F、質量比S、厚度比T、 基底模量E1和復合梁損耗因子ηc的隨機誤差均取為0.5%, 使用式(1)和式(2)反演阻尼層的楊氏模量和損耗因子。
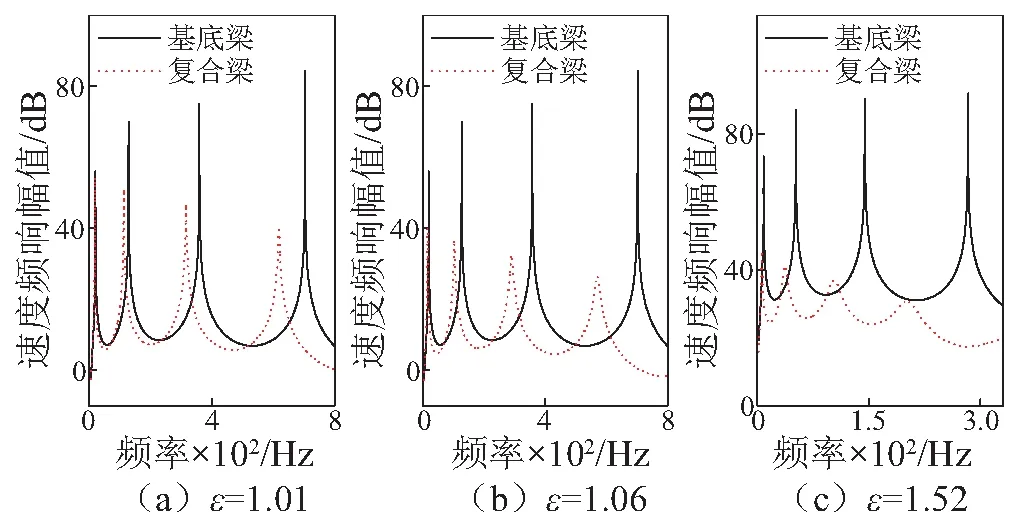
圖3 三個試件仿真頻響曲線Fig.3 Simulated velocity frequency response of the three specimens
圖4為三個試件反演結果的對比。可見隨著剛度比增大,楊氏模量和損耗因子的反演誤差均減小。表1為誤差的具體值,其中實際值由圖4數(shù)據(jù)計算得到,一階和高階估計分別是式(8)和式(12)的預測結果。由表1可知,楊氏模量的誤差預測值與實際值接近,且一階與高階估計差別很小。對于損耗因子,當ε較小時,一階估計的誤差預測值偏大,隨著ε變大,一階和高階估計的結果趨向實際值。整體而言,隨著剛度比增大,反演精度明顯提高。
進一步分析可知,試件1反演誤差大的主要原因是剛度比ε接近于1,導致F、S的誤差急劇放大。針對試件1,將頻率比F、質量比S的隨機誤差減至0.1%,同時保持厚度比T、基底模量E1和復合梁損耗因子ηc的隨機誤差不變,進行反演。

圖4 三個試件反演結果對比Fig.4 Comparison of the calculating results of the three specimens
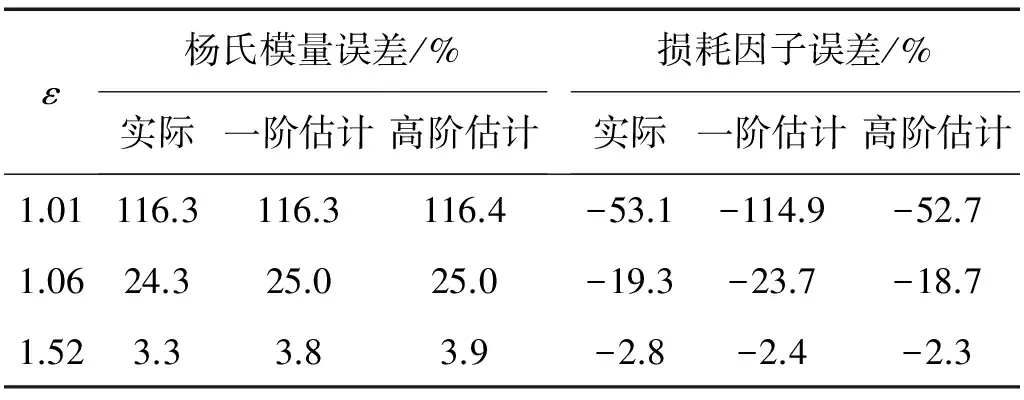
表1 三個試件反演誤差
圖5為頻率比F、質量比S誤差減小前后,楊氏模量和損耗因子反演結果的對比。可見F、S誤差減小后,反演誤差明顯變小。表2為誤差的具體值,其中總誤差由圖5數(shù)據(jù)計算,F(xiàn)、S的誤差放大量根據(jù)式(12)計算。對比總誤差與F、S的誤差放大量可知,總誤差幾乎全部由F、S的誤差引起。因此,當ε較小時,為保證阻尼層楊氏模量和損耗因子的反演精度,應嚴格控制試件共振頻率和質量的測量誤差。
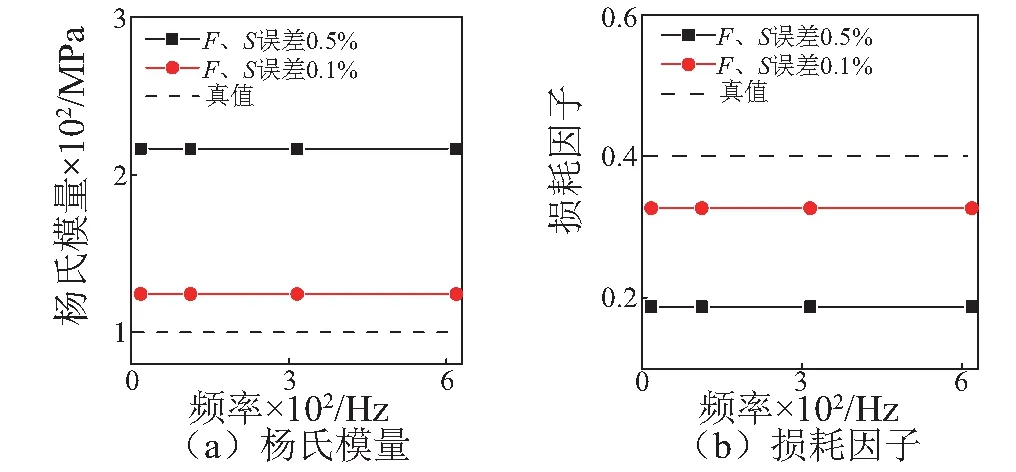
圖5 頻率比F、質量比S誤差對反演結果影響Fig.5 Effects of the errors of F and S on the calculating results

表2 頻率比F、質量比S誤差對反演精度影響
4 試驗驗證
為進一步驗證分析的結果,使用兩組剛度比不同的試件測量了聚氨酯橡膠材料的特性。兩組試件的基底層均為不銹鋼,其厚度分別為1 mm和0.5 mm,聚氨酯橡膠的厚度均為2 mm,因厚度比不同,兩組試件剛度比ε產(chǎn)生差異,分別約為1.03和1.13。第一組試件基底層和阻尼層質量分別為8.2 g和10.1 g,第二組分別為16.4 g和10.3 g。試件長度和寬度分別為225 mm和10 mm。測量的頻率間隔為0.25 Hz,質量測量精確到0.1 g。
圖6為測得的頻響曲線。從圖中識別出共振頻率比F和復合梁的損耗因子ηc,然后反演阻尼層的楊氏模量和損耗因子。
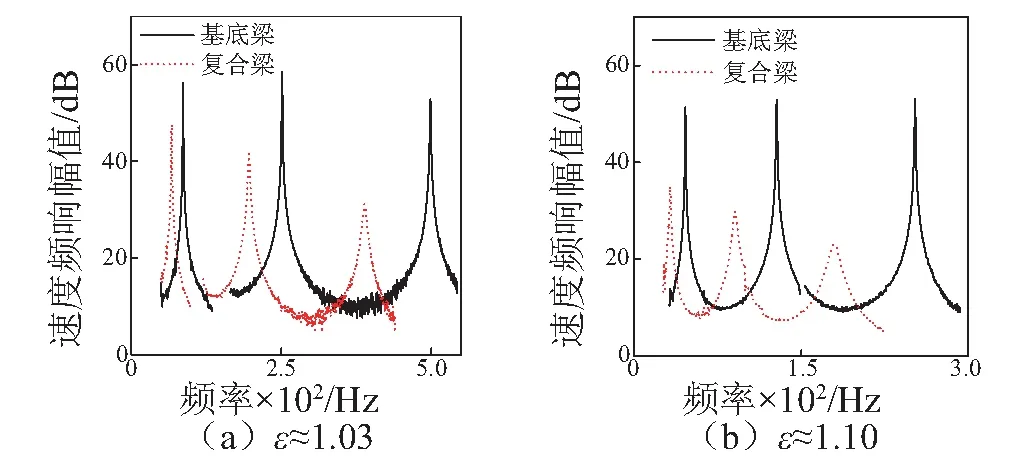
圖6 兩組試件頻響曲線Fig.6 Experimental velocity frequency response of the two specimens
圖7為楊氏模量和損耗因子的反演結果,圖中實心標記為實測數(shù)據(jù)的反演結果。兩組結果存在一定差異,這是由第一組剛度比ε較小引起的,因為小的剛度比會導致測量誤差急劇放大,例如,計算可得第一組質量比S的誤差放大倍數(shù)約為33倍,而第二組僅為8倍。為對此進行驗證,假定阻尼層質量存在0.1 g的測量誤差,重新反演可得到空心標記的結果。可見對于第一組,楊氏模量和損耗因子的結果均有較大偏移,而第二組的偏移量明顯更小。這證明了相同測量誤差條件下,當剛度比值較大時,有利于提高測量的穩(wěn)定性,從而提高精度。同時也證明了質量比S是引起反演誤差的一個主要因素,類似地也可驗證頻率比F的影響。
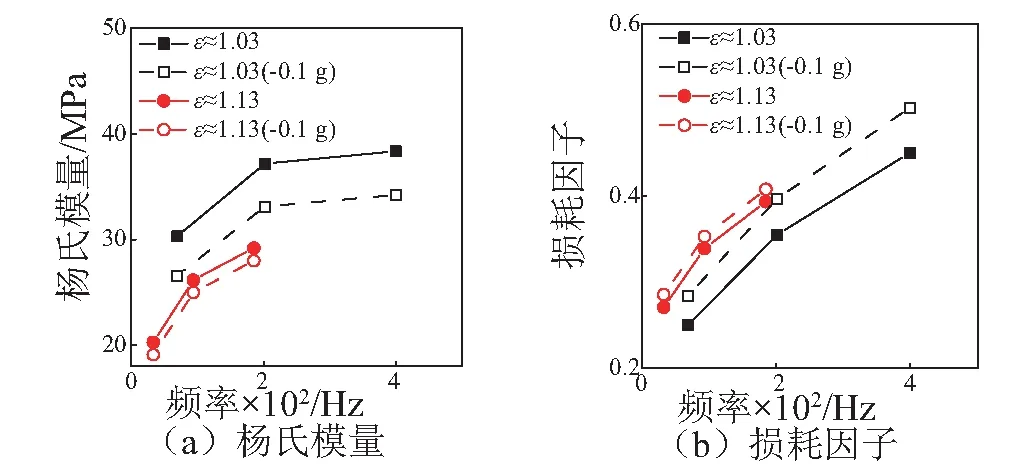
圖7 兩組試件反演結果對比Fig.7 Comparison of the calculating results of the two specimens
5 結 論
得到了雙邊自由阻尼梁阻尼層楊氏模量和損耗因子的簡化反演公式,并在此基礎上進行誤差分析,給出了高階誤差預測公式。研究表明:
(1) 復合梁與基底梁的剛度比ε是影響誤差放大的重要因素。相同測量誤差條件下,ε越大,楊氏模量和損耗因子反演精度越高。
(2) 通過增大厚度比T和模量比e可以增大剛度比ε,從而提高反演精度。
(3) 當剛度比ε較小時,頻率比F與質量比S的誤差是引起反演誤差的主要因素。
(4) 使用高階誤差預測公式,可以對楊氏模量和損耗因子的誤差進行準確預測。
[ 1 ] JONES, DAVID I G. Handbook of viscoelastic vibration damping[M]. [S.l.]: Wiley, 2001: 259-262.
[ 2 ] 黃志誠,秦朝燁,褚福磊. 附加黏彈阻尼層的薄壁構件振動問題研究綜述[J]. 振動與沖擊, 2014, 33(7): 105-113.
HUANG Zhicheng, QIN Zhaoye, CHU Fulei. A review about vibration problems of thin-walled structures with viscoelastic damping layer[J]. Journal of Vibration and Shock, 2014, 33(7): 105-113.
[ 3 ] RENAULT A, JAOUEN L, SGARD F. Characterization of elastic parameters of acoustical porous materials from beam bending vibrations[J]. Journal of Sound and Vibration, 2011, 330(9): 1950-1961.
[ 4 ] 尹邦輝,王敏慶,吳曉東. 結構振動阻尼測試的衰減法研究[J]. 振動與沖擊, 2014, 33(4): 100-106.
YIN Banghui, WANG Minqing , WU Xiaodong. Decay method for measuring structural vibration damping[J]. Journal of Vibration and Shock, 2014, 33(4): 100-106.
[ 5 ] PEREIRA R, ARENAS J P, ZUMELZU E. Comparison of four test methods to measure damping properties of materials by using piezoelectric transducers[J]. Materials amp; Design, 2011, 32(4): 2423-2428.
[ 6 ] Standard test method for measuring vibration damping properties of materials: ASTM E756-05 [S]. [S.l.]: American Society for Testing and Materials, 2010.
[ 7 ] 聲學材料阻尼性能的彎曲共振測試方法: GB/T 16406—1996 [S]. 北京:國家技術監(jiān)督局,1996.
[ 8 ] 朱蓓麗, 沈慶元. 黏彈性材料復剪切模量的測量及誤差分析[J]. 噪聲與振動控制, 1999(6): 38-41.
ZHU Beili, SHEN Qingyuan. Measurement of the viscoelastic material’s complex shear modulus and the error analysis[J]. Journal of Noise and Vibration Control, 1999(6): 38-41.
[ 9 ] 馬少璞, 王敏慶, 胡衛(wèi)強,等. 對稱夾層結構的共振梁法理論誤差研究[J]. 噪聲與振動控制, 2008,28(4): 38-41.
MA Shaopu,WANG Minqing, HU Weiqiang, et al. Study on theoretical error of the resonance beam testing method about sandwich specimen[J]. Journal of Noise and Vibration Control, 2008,28(4): 38-41.
[10] 胡衛(wèi)強, 王敏慶, 劉志宏. 懸臂梁彎曲共振法自由阻尼結構試件設計研究[J]. 實驗力學, 2008, 23(3): 241-247.
HU Weiqiang, WANG Minqing, LIU Zhihong. Study of the design of free-damping form specimen in resonance method[J]. Journal of Experimental Mechanics,2008,23(3): 241-247.
[11] 王超, 呂振華. 黏彈性阻尼材料力學參數(shù)測試實驗用雙邊附加自由結構阻尼試件設計方法研究[J]. 振動與沖擊, 2014, 33(5): 102-108.
WANG Chao, Lü Zhenhua. Research on the design of specimens damped both sides used in the measurement of viscoelastic material’s mechanical parameters[J]. Journal of Vibration and Shock, 2014, 33(5): 101-108.
Erroranalysisofthesymmetricfree-layerbeammethodfordeterminingYoung’smodulusandlossfactorofdampingmaterials
QU Zhongpeng, SHENG Meiping
(School of Marine Science and Technology, Northwestern Polytechanical University, Xi’an 710072, China)
The inverse formulas of the symmetric free-layer beam method were simplified by introducing the medium variables. Based on the simplified formulas, a total error analysis was made and the higher order expressions for error prediction were derived. The research shows that the stiffness ratio is the most significant factor influencing the inverse accuracy. More accurate results can be obtained from specimens with bigger stiffness ratios. The errors of the frequency ratio and the mass ratio are violently magnified as the stiffness ratio reaches 1, which will lead to great inverse errors. The stiffness ratio can be increased by increasing the thickness ratio and the modulus ratio between the damping and the base layer. Thus the inverse accuracy will be improved. The conclusion was verified by simulation analysis.
damping materials; flexural resonance method; symmetric free-layer beam; error analysis; stiffness ratio
2016-05-30 修改稿收到日期: 2016-09-07
屈忠鵬 男,博士生,1989年生
盛美萍 女,博士,教授,1970年生
TB535.1
A
10.13465/j.cnki.jvs.2017.22.016

