基于變分模態分解和排列熵的滾動軸承故障診斷

鄭小霞， 周國旺， 任浩翰， 符 楊

(1.上海電力學院 自動化工程學院，上海 200090； 2. 上海東海風力發電有限公司，上海 200090)

基于變分模態分解和排列熵的滾動軸承故障診斷

鄭小霞1， 周國旺1， 任浩翰2， 符 楊1

(1.上海電力學院 自動化工程學院，上海 200090； 2. 上海東海風力發電有限公司，上海 200090)

滾動軸承早期故障信號特征微弱且難以提取，為了從軸承振動信號中提取特征參數用于軸承故障診斷和識別，提出基于變分模態分解(Variational Mode Decomposition,VMD)和排列熵(Permutation Entropy, PE)的信號特征提取方法，并采用支持向量機(Support Vector Machine,SVM)進行故障識別。對軸承振動信號進行變分模態分解，得到不同尺度的本征模態函數；計算各本征模態函數的排列熵，組成多尺度的復雜性度量特征向量；將高維特征向量輸入基于支持向量基建立的分類器進行故障識別分類。通過滾動軸承實驗數據分析了算法中參數選取問題，將該方法應用于滾動軸承實驗數據，并與集合經驗模態分解和小波包分解進行對比，分析結果表明，基于變分模態分解和排列熵的診斷方法有更高的診斷準確率，能夠有效實現滾動軸承的故障診斷。

變分模態分解；排列熵；支持向量機；滾動軸承；故障診斷

滾動軸承是機械設備中廣泛應用的零部件，其運行狀態好壞將直接影響設備的生產效率和安全。在機械設備實際運行中，若不能及時發現滾動軸承早期故障，其故障產生的沖擊會加速滾動軸承的損壞，最終導致滾動軸承失效，對機械正常運行帶來嚴重影響。因此，對滾動軸承運行狀態監測與診斷，尤其是滾動軸承早期故障診斷具有十分重要的意義[1]。

變分模態分解(Variational Mode Decomposition，VMD)是由Dragomiretskiy等[2]提出的一種自適應信號處理方法，通過迭代搜尋變分模態的最優解，不斷更新各模態函數及中心頻率，得到若干具有一定帶寬的模態函數。與經驗模態分解(Empirical Mode Decomposition, EMD)[3]遞歸篩選方法不同，VMD通過求解變分模態最優解實現模態分解，有堅實的理論基礎；并且與小波變換不同，不用選取基函數；VMD實質是多個自適應維納濾波器組，對噪聲有較好的魯棒性；在信號分離方面，VMD能成功分離兩個頻率相近的純諧波信號。已有學者將VMD法應用到了機械故障診斷領域，Wang等[4]研究了VMD 的等效波器組效應，并將其應用到轉子系統碰摩故障檢測，通過仿真信號和實際燃氣輪機振動信號分析表明了VMD 方法能更好的提取信號的特征信息；唐貴基等[5]通過參數優化的變分模態分解對振動信號進行分解，得到若干本征模態函數分量，對各分量包絡譜分析實現了滾動軸承故障的有效判別。

Christoph等[6]提出的排列熵(Permutation Entropy, PE)算法是一種檢測時間序列隨機性和動力學突變的方法，它具有計算簡單、抗噪聲能力強等特點。而振動信號往往具有非線性、非平穩性特征，已有學者將排列熵用于機械振動信號突變檢測并取得較好效果。劉永斌等[7]研究了不同工作狀態下軸承振動信號的排列熵，結果表明排列熵可以有效地檢測出機械設備狀態變化。由于機械系統振動信號中包含豐富的特征信息，僅在單一尺度上很難提取到微弱的故障特征信息，有必要對振動信號進行多尺度分析[8]。排列熵與其他算法相結合對信號進行多尺度分析成為研究的熱點，如與小波變換[9]、集合經驗模態分解[10]結合對滾動軸承進行故障診斷分析。

由于軸承早期故障特征信息微弱，僅檢測原始信號的動力學突變不能全面反映信號各模態的細節特征。針對滾動軸承故障振動信號特征的特點，將變分模態分解與排列熵信息測度相結合應用于滾動軸承故障信號特征提取。將原始振動信號用VMD方法分解得到若干本征模態函數，提取各模態分量的排列熵，可以更好的反應信號在不同尺度上的細節復雜度特征。并采用支持向量機(Support Vector Machine,SVM)進行故障狀態識別，從而實現滾動軸承故障類別的診斷。該方法集合了VMD算法在信號分解方面的優勢和排列熵檢測復雜系統動力突變的特點，并將其應用于軸承實驗數據，結果表明，提出的方法能夠有效的區分滾動軸承故障類型，是一種有效的故障診斷方法。

1 VMD原理

VMD是一種比EMD和LMD (Local Mean Decomposition) 有更好時頻分布的信號分解估計方法，其整體框架是變分問題，根據預設模態分量個數對信號進行分解。將原始信號f(x)分解為K個中心頻率為ωk模態函數uk，其中K為預設模態分量個數。VMD算法中，重新定義本征模態函數(Intrinsic Mode Function, IMF)為一個調幅-調頻信號

uk(t)=Ak(t)cos(φk(t))

(1)

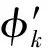
為了得到具有一定帶寬頻率的K個模態分量，首先對每個模態函數uk，通過Hilbert變換得到邊際譜；然后對各模態解析信號混合一預估中心頻率，將每個模態的頻譜調制到相應的基頻帶；再計算解析信號梯度的平方L2范數，估計出各模態信號帶寬，受約束的變分問題為

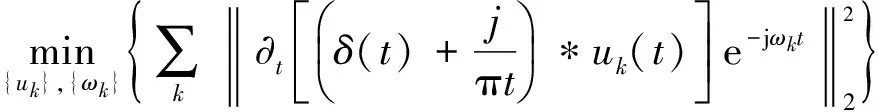
(2)

式中：{uk}={u1,u2,…,uK}為分解得到的K個模態分量；{ωk}={ω1,ω2, …，ωK}為各分量的頻率中心；δ(t)為脈沖函數。

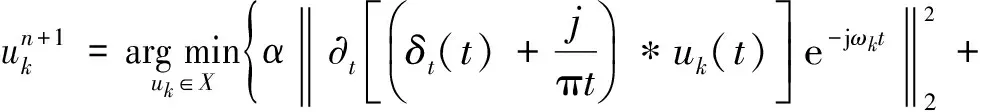
(3)

式中：α為懲罰參數；λ為Lagrange乘子。

利用Parseval/Plancherel傅里葉等距變換，將式(2)轉變到頻域

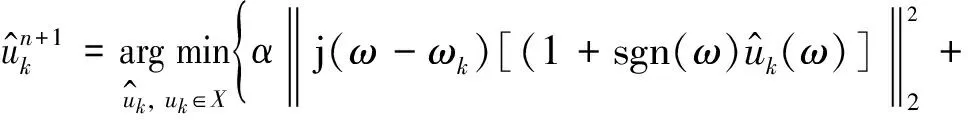
(4)

經進一步轉換可以得到二次優化問題的解為

(5)

式中，ωk為當前模態函數功率譜的重心，從式(5)可知，維納濾波器被嵌入了VMD算法中，算法有更好的噪聲魯棒性。

對于中心頻率ωk的取值問題可表達為

(6)

根據同樣的過程，首先將中心頻率的取值問題轉換到頻域

(7)

中心頻率二次優化問題的解為

(8)

VMD算法步驟如下：

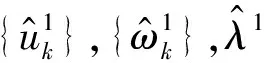
步驟2 根據式(5)和式(8)更新uk和ωk；

步驟3 更新λ

(9)

2 排列熵原理

熵是源于物理學的概念，是對系統內部紊亂程度的度量，熵值越大，表明系統越復雜。排列熵是一種衡量一維時間序列復雜度的平均熵參數，它與LyaPunov指數、分形維數等復雜度參數相比，具有計算簡單、抗噪聲能力強、計算值穩定等優點[11-12]。

排列熵算法原理如下：對于一個時間序列{X(i),i=1, 2,…，N}進行相空間重構，得到矩陣

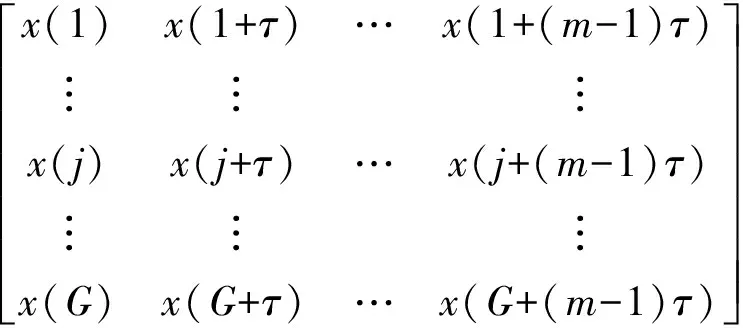
(10)

式中：m為嵌入維數；τ為延遲時間；G為重構相空間中重構向量個數，G=N-(m-1)τ。矩陣中的每一行可看作一個重構分量，共有G個重構分量。將重構矩陣中的第j重構分量{x(j),x(j+τ),…,x(j+(m-1)τ)}按照升序重新排列，即

{x(i+(j1-1)τ)≤x(i+(j2-1)τ)≤…≤x(i+(jm-1)τ)}

(11)

式中，j1,j2,…,jm為重構分量中各元素所在列的索引。

如果重構分量中存在相等的值，如x(i+(jp-1)τ)=x(i+(jq-1)τ)，則按照jp和jq原來的順序，即當jplt;jq時，有x(i+(jp-1)τ)≤x(i+(jq-1)τ)。所以對于重構相空間中的任意一個重構向量X(j)都可以得到一個反映其元素大小順序的符號序列S(l)=[j1,j2, …,jm]，其中l=1, 2, …,g，且g≤m!。m維相空間映射不同符號序列[j1,j2, …,jm]共有m!個，S(l)是其中的一種排列形式。構造序列P1,P2, …,Pg，Pg為第g種符號序列出現的概率大小。對于一個時間序列{X(i),i=1, 2, …，N}的g個重構向量對應的符號序列的排列熵(PE)，可以按照Shannon熵的形式定義為

(12)

當Pl=1/m!時，PE(m)達到最大值ln(m!)。通常情況下，可通過ln(m!)將Hp(m)標準化，即

PE=PE(m)/ln(m!)

(13)

式中，PE的取值范圍為0≤PE≤1。PE值的大小表示時間序列{X(i),i=1, 2, …,N}的復雜和隨機程度：PE值越大，時間序列越接近隨機；PE值越小，時間序列越規則。

3 基于SVM的軸承故障診斷

SVM是在統計學理論基礎上發展起來的一種通用機器學習方法[13]。SVM法實質是尋找一個最優分類超平面，使得從這個超平面到兩類樣本集的距離之和最大。SVM本身是一個二類問題判別方法，對于多類問題需要對二分類問題進行轉換。文中采用“一對多”的方法[14]對實現SVM多分類問題的轉換。其基本思想是對于n個類別的分類問題需要構造個n兩分類機，其中第i個分類機能把第i類同余下的各類劃分開。

本文結合VMD對信號分解的優點和排列熵能檢測時間序列隨機性和動力學突變特點，提出基于SVM的滾動軸承故障識別方法。首先將原始振動信號進行VMD分解，得到若干個本征模態分量，再計算各模態分量的排列熵，最后將排列熵值作為特征向量輸入支持向量機分類器進行故障分類識別。基于變分模態分解和排列熵的滾動軸承故障診斷流程圖，如圖1所示。具體步驟如下：

步驟1 在滾動軸承正常狀態、內圈故障、外圈故障、滾動體故障狀態下，按照一定的采樣頻率分別進行重采樣，得到各狀態下的振動數據樣本。

步驟2 對軸承四種狀態下的振動信號數據進行VMD分解，得到各狀態下的不同尺度模態分量。

步驟3 計算各尺度模態分量復雜度特征的排列熵測度PEi(i=1, 2, …，K),并構建高維特征向量

PE=[PE1，PE2，…，PEK]

(14)

步驟4 將得到的高維特征向量輸入SVM進行訓練，得到每一類型故障的SVM預測模型。

步驟5 采集測試信號，按照步驟1、步驟2、步驟3構建測試樣本高維特征向量，分別輸入訓練好的4個SVM預測模型，通過SVM分類器的輸出結果來確定軸承的故障類型和工作狀態。

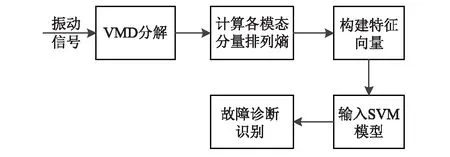
圖1 滾動軸承故障診斷流程圖Fig. 1 Flow chart of rolling bearing fault diagnosis

4 算法關鍵參數選取及實驗分析

為了驗證變分模態分解和排列熵方法的有效性，采用美國凱斯西儲大學電氣工程實驗室的滾動軸承數據進行實驗數據分析。選用的滾動軸承為6205-2RS JEM SKF型深溝球軸承，振動數據采樣頻率為12 kHz、電機負載為1 HP。試驗用電火花加工技術在軸承上布置單點故障，故障點的直徑為0.177 8 mm，故障深度為0.279 4 mm。采集正常狀態、內圈單點電蝕、外圈單點電蝕、和滾動體單點電蝕四種狀態的振動信號。

4.1 模態個數確定

用VMD算法進行信號分解時，需要首先確定模態個數K，不同的分解個數對分解的結果會產生影響，從而影響最終的診斷。模態分解個數較少時，由于VMD算法相當于自適應維納濾波器組，原始信號中一些重要信息將會被濾掉丟失；信號的分解個數較多時，相鄰模態分量的頻率中心則會相距較近，產生頻率混疊。選用滾動體單點電蝕故障信號進行VMD分解，不同K值下的中心頻率如表1所示。從表中可以看出，在模態分量個數為5時，中心頻率3 213 Hz和3 415 Hz相距較近，可能會出現模態混疊，模態個數選為4較適宜。

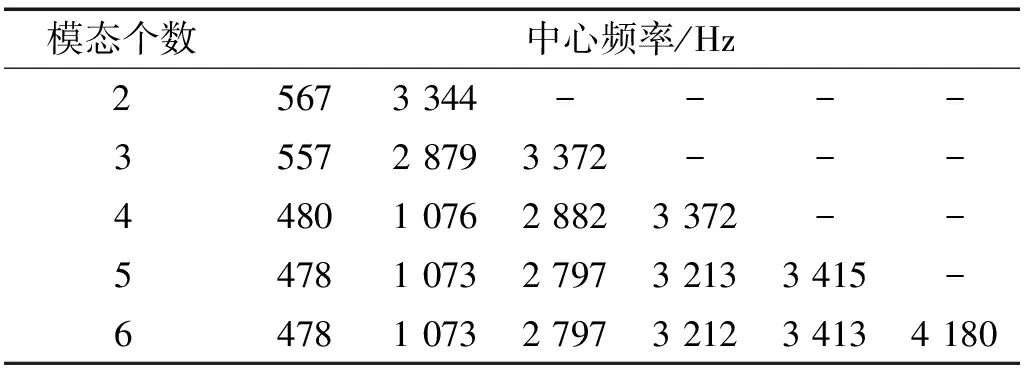
表1 不同K值對應的中心頻率

4.2 懲罰參數的選取

VMD算法中懲罰參數對分解結果也有較大影響，研究發現：懲罰參數α越小，得到的各IMF分量帶寬越大，反之，α越大各分量帶寬越小。本文引入信噪比概念，用來分析懲罰參數對VMD算法分解結果的影響。信噪比指原始信號能量與噪聲能量的比值，記為SNR(Signal Noise Ratio)

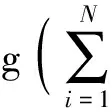
(15)

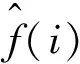
對軸承振動信號做不同征罰參數的VMD分解，并計算其信噪比值，如圖2所示。從圖2可知，信號的信噪比隨著懲罰參數α的增大而減小，并趨于平穩。信噪比的變化與各模態分量帶寬范圍隨α的改變相一致。從信號分解的角度來說，重構后的信號能真實的還原原始信號，這就要求選取較大的信噪比。從信號濾波角度來說，希望分解算法有一定的噪聲魯棒性，對信號分角重構后能濾除噪聲，此時又要求信噪比不能過大。通過對大量軸承振動信號測試分析，本文選取懲罰參數α=2 000，以保證VMD分解過程中的去噪能力和細節保留度。對軸承振動信號的分解結果如圖3所示。

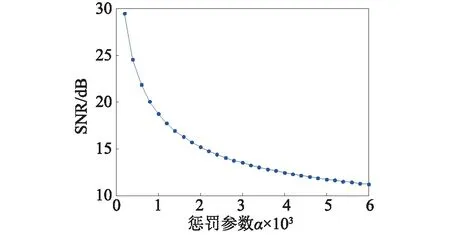
圖2 不同懲罰參數下振動信號信噪比Fig.2 The SNR of vibration signal with different penalty parameter

圖3 軸承振信號VMD分解結果Fig.3 VMD decomposition results of the rolling bearing vibration signal

4.3 排列熵參數的選取

在排列熵的計算中，需要考慮和設定3個參數值，即時間序列長度N，嵌入維數m和時延τ，不同參數的選取對熵值的計算結果會產生影響。

為了研究時延τ對排列熵計算數值的影響，以長度為1 024的軸承振動信號為例，在不同τ下的排列熵值隨嵌入維數的變化關系，如圖4所示。由圖4可知，當時延τ在1～6變化時，信號的排列熵數值變化很小，時延τ對排列熵值影響較小，論文中計算排列熵時取τ=1。

Christoph等建議，嵌入維數m的取值為3～7。因為，如果m=1或m=2時，重構向量狀態個數較少，不能精確檢測信號動力學突變；當m取值過大，相空間的重構將會均勻化時間序列，這時排列熵的計算量增大并且不宜反映時序列的微小變化。Cao 等[15]研究指出當嵌入維數m=5，m=6或m=7時，排列熵的值能夠很好的表征時間序列的動態特性。論文中，選取嵌入維數m=6。

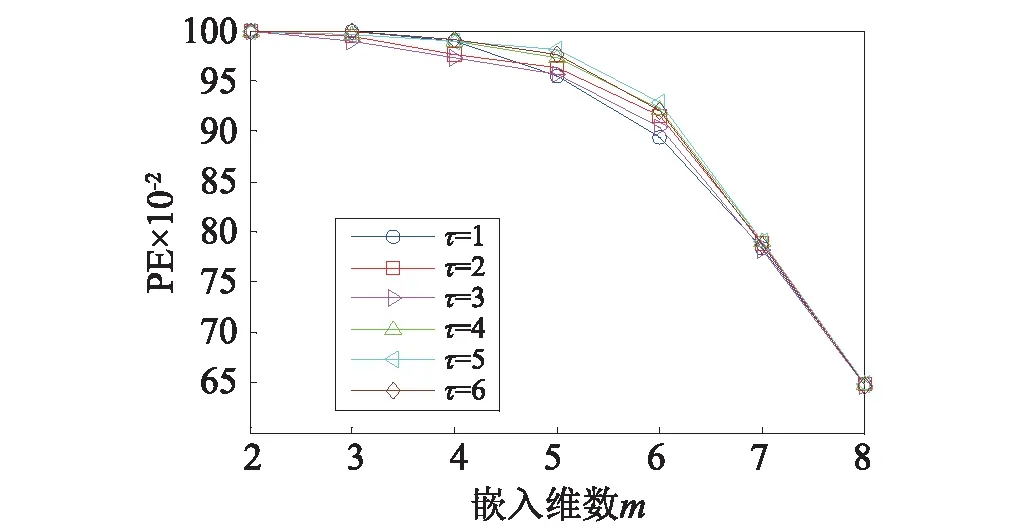
圖4 振動信號在不同時延下的排列熵Fig.4 The PE of vibration signal with different time delays

圖4為在時延τ=1時，不同數據長度的振動信號在不同嵌入維數下的排列熵值，振動信號的數據長度分別為256，512，1 024，2 048和4 096。從圖5可知，在嵌入維數m≤5時，除了數據長度為256時的排列熵外，其他數據長度的排列熵值隨嵌入維數的增加變化較小，排列熵值也十分接近。當嵌入維數m=6時，其不同長度的振動信號排列熵及其差值，如表2所示。從表2可知，隨信號長度的增加，其排列熵差值減小，排列熵值在數據長度大于1 024時趨于穩定，選擇數據長度為2 048較為合適。

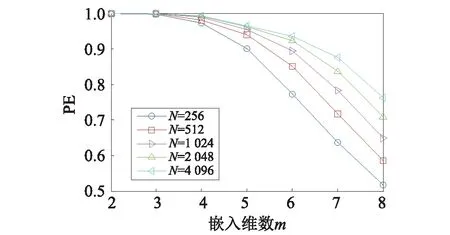
圖5 不同長度的振動信號的排列熵Fig.5 The PE of vibration signal with different lengths

表2 不同長度的振動信號排列熵及其差值

4.4 軸承故障診斷

對正常、內圈故障、外圈故障、滾動體故障四種狀態軸承的振動信號，每種狀態取40組數據，數據樣本長度為2 048，共160組數據。從每種狀態樣本數據中隨機抽取25%的數據，即10組數據作為訓練樣本，將剩下的正常、內圈故障、外圈故障、滾動體故障四種狀態軸承振動信號各30組數據作為測試樣本。

對訓練樣本數據進行VMD分解，每個訓練樣本得到的4個模態分量提取排列熵，共可得到40×4個排列熵值。將每個訓練樣本得到的4個排列熵組成一個特征向量，得到40個特征向量的平均值如圖6所示。將40個特征向量作為輸入量，輸入SVM分類器進行訓練。構造4個兩分類SVM，依次取每種狀態下的排列熵特征向量作為正類，剩余三種狀態的排列熵特征向量作為負類，輸入SVM分類器進行訓練，得到4個訓練好的SMV預測模型。

圖6 特征向量排列熵值Fig.6 The PE of the feature vectors

將四種狀態軸承振動信號測試樣本共120組用訓練好的SVM分類器進行分類，識別準確率達97.5%，其分類結果如表3所示。從表3可知，有一個內圈故障被診斷為滾動體故障，兩個外圈故障被診斷為內圈故障，但對于正常狀態和滾動體故障狀態的識別準確率為100%。

由于美國凱斯西儲大學滾動軸承信號為實驗室環境采集的較為規整信號，而實際工況中軸承振動信號中含有很強的噪聲。本文通過對軸承振動信號加入高斯白噪聲，研究所提出方法對噪聲的魯棒性。對四種狀態軸承振動信號分別添加信噪比為6 dB 的高斯白噪聲，再用本文所提出的方法對信號進行分解和特征提取，對軸承狀態進行識別，其結果如表4所示。由于噪聲的影響，內圈故障識別率較低，有6個樣本被識別為外圈故障。但其他狀態的正確率為100%，平均識別正確率也能達到95%，說明所提出的方法對噪聲有一定的魯棒性。

為了研究采用不同比例訓練樣本時，對滾動軸承運行狀態分類識別結果的影響，選取上述美國凱斯西儲大學滾動軸承四種狀態下振動數據共160組，在正常狀態、內圈故障、外圈故障和滾動體故障樣本數據中隨機抽取20%、30%、40%、50%、60%的數據作為訓練樣本數據，將剩下的樣本數據作為測試樣本。表5為不同訓練樣本下的分類結果，可以看出當訓練數據為樣本數據的50%時，所提出方法的診斷正確率可達到100%。當訓練樣本增大時，建立的分類模型較準確，識別度較高，但會增加算法的計算量。

為了對比VMD的分解在故障診斷方法中的作用，對上述滾動軸承四種類型振動信號采用集合經驗模態(Ensemble EMD, EEMD)和小波包進行分解。振動信號數據源選取和特征提取方法與本文所用處理過程相同。為了方便比較，對于EEMD 分解得到的模態分量選取包含主要信息的前4個模態分量，小波包分解采用兩層分解得到4組小波系數。計算分解得到的各分量和排列熵，并組成特征向量。將特征向量輸入SVM 進行訓練和測試，其結果如表6和表7所示。

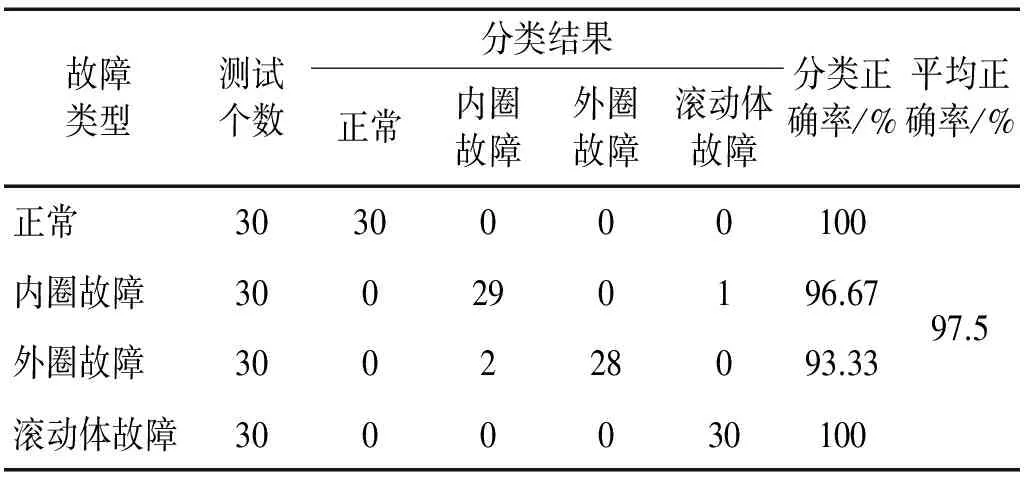
表3 基于VMD和排列熵的滾動軸承故障識別結果

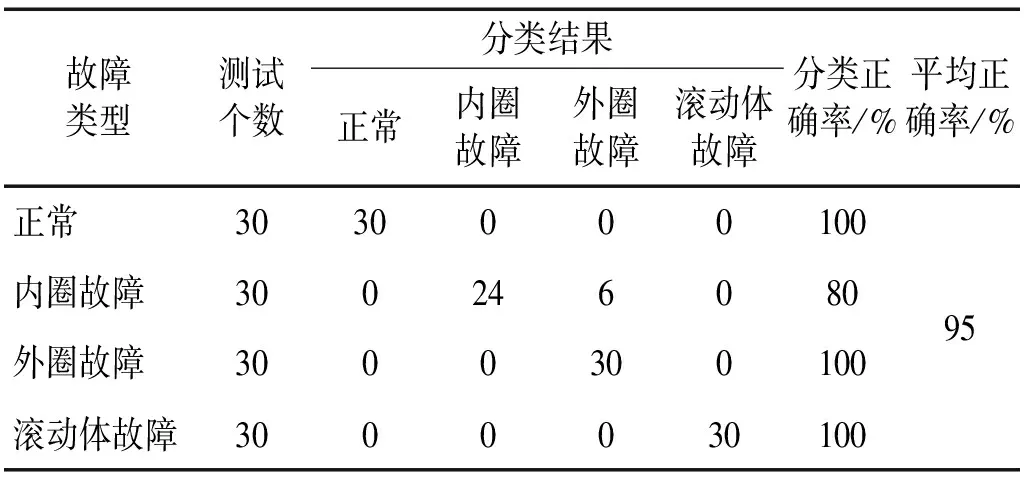
表4 添加白噪聲后滾動軸承故障識別結果

表5 不同訓練樣本數下故障識別結果

表6 基于EEMD和排列熵的滾動軸承故障識別結果

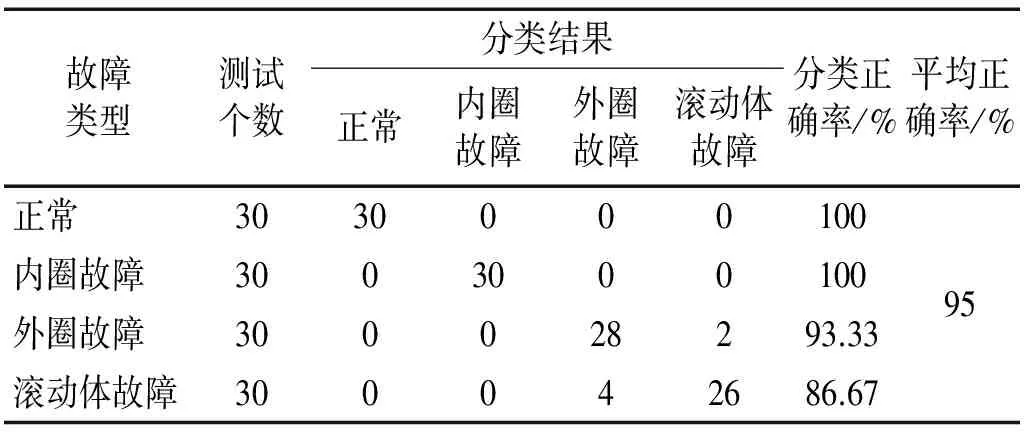
表7 基于WPD和排列熵的滾動軸承故障識別結果

從表6可知，采用EEMD分解方法時，對正常狀態、內圈故障和滾動體故障的識別正確率都達到了100%，但對外圈故障的識別正確率較低，有5個被診斷為內圈故障，使得平均識別正確率低于采用VMD方法，平均識別正確率為95.83%。采用小波包分解方法時，正常狀態和內圈故障的診斷正確率也達到了100%，但有兩個內圈故障被診斷為滾動體故障，4 個滾動體故障被診斷為內圈故障，平均正確率為95%，低于EEMD方法和VMD方法。所以，基于VMD方法對信號進行分解，提取排列熵，對滾動軸承故障診斷效果要優于EEMD和小波包分解方法。

5 結 論

本文針對滾動軸承的正常、內圈故障、外圈故障、滾動體故障診斷識別問題，提出一種基于變分模態分解和排列熵的故障診斷識別方法，對振動信號進行VMD分解，對得到的模態分量求取其排列熵，并作為特征向量輸入SVM，實現故障診斷識別。通過對滾動軸承信號進行診斷分析，得出如下結論：

(1) 將VMD 方法應用到滾動軸承振動信號分析中，能夠將信號分解為具有一定帶寬頻率的模態分量，為后續的特征提取和故障分類識別提供無模態混疊現象且特征信息豐富的數據源。

(2) 排列熵能夠檢測信號隨機性和動力學突變行為，并與VMD結合提出一種新的故障診斷方法，對滾動軸承信號分析表明該方法能對正常狀態、內圈故障、外圈故障和滾動體故障進行有效識別。

(3) 通過采用EEMD和小波包對振動信號分解，再按本文所提方法進行特征提取和故障分類識別，并與本文所提方法進行對比，結果表明基于變分模態分解和排列熵的診斷方法有更高的準確率，診斷效果更好。

[ 1 ] 唐貴基, 龐彬, 劉尚坤. 基于奇異差分譜和平穩子空間分析的滾動軸承故障診斷[J]. 振動與沖擊, 2015，34(11): 83-87.

TANG Guiji, PANG Bin, LIU Shangkun. Fault diagnosis of rolling bearings based on difference spectrum of singular value and stationary subspace analysis [J]. Journal of Vibration and Shock, 2015, 34(11): 83-87.

[ 2 ] DRAGOMIRETSKIY K, ZOSSO D.Variational mode decomposition [J]. IEEE Tran on Signal Processing,2014，62(3): 531-544．

[ 3 ] HANG N E,WU M,LONG S R,et al. The empirical mode decomposition and the hilbert spectrum for nonlinear and non-stationary time series analysis [J]. Proceedings of the Royal Society of London,1998, 454(1971): 903-995．

[ 4 ] WANG Y, MARKERT R, XIANG J, et al. Research on variational mode decomposition and its application in detecting rub-impact fault of the rotor system [J]. Mechanical Systems amp; Signal Processing, 2015, 60/61: 243-251.

[ 5 ] 唐貴基, 王曉龍. 參數優化變分模態分解方法在滾動軸承早期故障診斷中的應用[J]. 西安交通大學學報, 2015, 49(5): 73-81.

TANG Guiji, WANG Xiaolong. Parameter optimized variational mode decomposition method with application to incipient fault diagnosis of rolling bearing [J]. Journal of Xi’an Jiaotong University, 2015, 49(5): 73-81.

[ 6 ] CHRISTOPH B, BERND P. Permutation entropy: a natural complexity measure for time series [J]. Physical Review Letters, 2002, 88(17): 174102.

[ 7 ] 劉永斌, 龍潛, 馮志華,等. 一種非平穩、非線性振動信號檢測方法的研究[J]. 振動與沖擊, 2007, 26(12): 131-134.

LIU Yongbin, LONG Qian, FENG Zhihua, et al. Detection method for nonlinear and non-stationary signals [J]. Journal of Vibration amp; Shock, 2007, 26(12): 131-134.

[ 8 ] 鄭近德, 程軍圣, 楊宇. 基于LCD和排列熵的滾動軸承故障診斷[J]. 振動、測試與診斷, 2014, 34(5): 802-806.

ZHENG Jinde, CHENG Junsheng, YANG Yu. A rolling bearing fault diagnosis method based on LCD and permutation entropy [J]. Journal of Vibration, Measurement amp; Diagnosis, 2014, 34(5): 802-806.

[ 9 ] 馮輔周, 司愛威, 饒國強,等. 基于小波相關排列熵的軸承早期故障診斷技術[J]. 機械工程學報, 2012, 48(13):73-79.

FENG Fuzhou, SI Aiwei, RAO Guoqiang, et al. Early fault diagnosis technology for bearing based on wavelet correlation permutation entropy[J]. Journal of Mechanical Engineering, 2012, 48(13): 73-79.

[10] ZHANG X, LIANG Y, ZHOU J. A novel bearing fault diagnosis model integrated permutation entropy, ensemble empirical mode decomposition and optimized SVM [J]. Measurement, 2015, 69: 164-179.

[11] FRANK B, POMPE B, SCHNEIDER U, et al. Permutation entropy improves fetal behavioural state classification based on heart rate analysis from biomagnetic recordings in near term fetuses [J]. Medical amp; Biological Engineering amp; Computing, 2006, 44(3): 179-187.

[12] YAN R, LIU Y, GAO R X. Permutation entropy: a nonlinear statistical measure for status characterization of rotary machines [J]. Mechanical Systems amp; Signal Processing, 2012, 29(5): 474-484.

[13] RIFKIN R, KLAUTAU A. In defense of one-vs-all classification[J]. Journal of Machine Learning Research, 2004, 5(1): 101-141.

[14] 姜萬錄, 吳勝強. 基于SVM和證據理論的多數據融合故障診斷方法[J]. 儀器儀表學報, 2010, 31(8): 1738-1743.

JIANG Wanlu, WU Shengqiang. Multi-data fusion fault diagnosis method based on SVM and evidence theory [J]. Chinese Journal of Scientific Instrument, 2010, 31(8): 1738-1743.

[15] CAO Y H, TUNG W W, GAO J B, et al. Detecting dynamical changes in time series using the permutation entropy [J]. Physical Review E , 2004, 70(4): 174-195.

Arollingbearingfaultdiagnosismethodbasedonvariationalmodedecompositionandpermutationentropy

ZHENG Xiaoxia1, ZHOU Guowang1, REN Haohan2, FU Yang1

(1. School of Automation Engineering, Shanghai University of Electric Power, Shanghai 200090, China；2. Shanghai Donghai Wind Power Co., Ltd., Shanghai 200090, China)

The incipient fault characteristic of rolling bearing vibration signals is weak and difficult to extract. In order to extract the characteristic parameters from a bearing vibration signal for bearing fault diagnosis, a signal characteristics extraction method based on the variational mode decomposition and permutation entropy was proposed. The support vector machine was used for fault recognition. Firstly, the bearing vibration signal was decomposed by the variational mode decomposition, and the intrinsic mode functions were obtained in different scales. Secondly, the permutation entropy of each intrinsic mode function was calculated and used to compose the multiscale feature vector. Finally, the high-dimensional feature vector was input to the support vector machine for bearing fault diagnosis. The comparison is made with EEMD and WPD(wavelet packet decomposition). The experimental results show that the proposed method can be used to diagnose bearing faults effectively.

variational mode decomposition; permutation entropy; support vector machine; rolling bearing; fault diagnosis

國家自然科學基金(51507098)；上海綠色能源并網工程技術研究中心(13DZ2251900)；上海市科委重點科技攻關項目(14DZ1200905)；上海市電站自動化技術重點實驗室項目(13DZ2273800)

2016-03-21 修改稿收到日期： 2016-06-06

鄭小霞 女，博士，副教授，1978年生

TH212；TH213.3

A

10.13465/j.cnki.jvs.2017.22.004