超臨界軸向運(yùn)動(dòng)Timoshenko梁橫向受迫振動(dòng)

譚 霞, 丁 虎, 陳立群,2

(1.上海大學(xué) 上海市應(yīng)用數(shù)學(xué)和力學(xué)研究所, 上海 200072； 2.上海大學(xué) 理學(xué)院，上海 200444)

超臨界軸向運(yùn)動(dòng)Timoshenko梁橫向受迫振動(dòng)

譚 霞1, 丁 虎1, 陳立群1,2

(1.上海大學(xué) 上海市應(yīng)用數(shù)學(xué)和力學(xué)研究所, 上海 200072； 2.上海大學(xué) 理學(xué)院，上海 200444)

研究外部激勵(lì)作用下，超臨界軸向運(yùn)動(dòng)Timoshenko梁橫向非線性振動(dòng)的穩(wěn)態(tài)響應(yīng)。通過對(duì)非零平衡位形的坐標(biāo)變換，從軸向運(yùn)動(dòng)Timoshenko梁的橫向振動(dòng)控制方程推導(dǎo)得到超臨界速度下受橫向外部激勵(lì)的陀螺系統(tǒng)標(biāo)準(zhǔn)控制方程。運(yùn)用Galerkin截?cái)喾〝?shù)值研究超臨界下軸向運(yùn)動(dòng)Timoshenko梁的穩(wěn)態(tài)周期幅頻響應(yīng)關(guān)系，并通過與超臨界速度下軸向運(yùn)動(dòng)Euler-Bernoulli梁的穩(wěn)態(tài)幅頻響應(yīng)曲線進(jìn)行對(duì)比，研究Euler-Bernoulli梁理論的適用范圍。

超臨界；軸向運(yùn)動(dòng)梁；Timoshenko理論；受迫振動(dòng)；Galerkin截?cái)喾?/p>

工程實(shí)際及生活中隨處可見軸向運(yùn)動(dòng)梁結(jié)構(gòu)，如機(jī)床傳動(dòng)帶、觀光纜車、機(jī)械傳送帶、發(fā)動(dòng)機(jī)等帶傳動(dòng)系統(tǒng)，通常都可簡(jiǎn)化為軸向運(yùn)動(dòng)梁模型。軸向運(yùn)動(dòng)梁作為最基本最典型的陀螺連續(xù)系統(tǒng)，其振動(dòng)分析與控制有著重要的理論研究意義。一系列優(yōu)秀的綜述反映了軸向運(yùn)動(dòng)體系的研究意義和研究成果[1-4]。

國(guó)內(nèi)外學(xué)者對(duì)亞臨界速度下軸向運(yùn)動(dòng)體系已經(jīng)有了比較系統(tǒng)的研究。宮蘇梅等[5]對(duì)于平帶系統(tǒng)的相關(guān)非線性振動(dòng)進(jìn)行了實(shí)驗(yàn)研究。呂海煒等[6]對(duì)軸向運(yùn)動(dòng)軟夾層梁橫向振動(dòng)進(jìn)行了分析研究。丁虎等[7-8]研究了軸向運(yùn)動(dòng)黏彈性梁的橫向非線性受迫振動(dòng)，運(yùn)用有限差分法研究了軸向運(yùn)動(dòng)梁非線性振動(dòng)的固有頻率。Ghayesh等[9]研究了轉(zhuǎn)動(dòng)慣量和溫度對(duì)軸向運(yùn)動(dòng)梁的非線性振動(dòng)、穩(wěn)態(tài)響應(yīng)和穩(wěn)定性的影響。隨著研究的深入和科技發(fā)展的要求，眾多學(xué)者越來越關(guān)注軸向運(yùn)動(dòng)系統(tǒng)高速運(yùn)動(dòng)狀態(tài)下的相關(guān)動(dòng)力學(xué)特性。Huang等[10]研究分析了超臨界速度下軸向穩(wěn)定運(yùn)動(dòng)梁的穩(wěn)定性。Ding等[11]運(yùn)用Galerkin截?cái)喾ㄑ芯康玫搅烁咚佥S向運(yùn)動(dòng)梁的固有頻率。以上研究高速軸向運(yùn)動(dòng)體系的文獻(xiàn)都是運(yùn)用的E-B(Euler-Bernoulli)梁理論，沒有考慮剪切力和轉(zhuǎn)動(dòng)慣量的影響。相對(duì)而言，對(duì)于Timoshenko梁的研究很少，高速軸向運(yùn)動(dòng)的Timoshenko梁理論研究就更加少見了。Tang等[12-13]研究了亞臨界下強(qiáng)弱外載荷作用下軸向運(yùn)動(dòng)黏彈性Timoshenko梁的非線性振動(dòng)，以及參數(shù)和外載荷作用下Timoshenko梁的非線性動(dòng)力學(xué)特性。他們的研究發(fā)現(xiàn)，在一定參數(shù)條件下，E-B梁理論和Timoshenko梁會(huì)產(chǎn)生顯著差別。

本文運(yùn)用Galerkin截?cái)喾ㄑ芯苛顺R界軸向運(yùn)動(dòng)Timoshenko梁橫向受迫振動(dòng)的穩(wěn)態(tài)響應(yīng)。并與超臨界速度下的E-B梁穩(wěn)態(tài)響應(yīng)進(jìn)行了對(duì)比，進(jìn)一步研究?jī)煞N梁理論間的異同，確定E-B梁理論在超臨界運(yùn)動(dòng)范圍內(nèi)的適用范圍。

1 數(shù)學(xué)模型和控制方程

圖1為超臨界軸向運(yùn)動(dòng)Timoshenko梁的物理模型。其中ρ為質(zhì)量密度；A為橫截面面積；E為彈性模量；EI為梁的彎曲剛度；G為剪切模量；I為關(guān)于中性軸的截面慣性矩；軸向坐標(biāo)X為離開左邊界的距離；V(X,T) 為橫向位移；T為是時(shí)間坐標(biāo)；P0為梁的初始軸向張力。 此外，梁以固定速度Γ軸向運(yùn)動(dòng)，梁長(zhǎng)為L(zhǎng)。

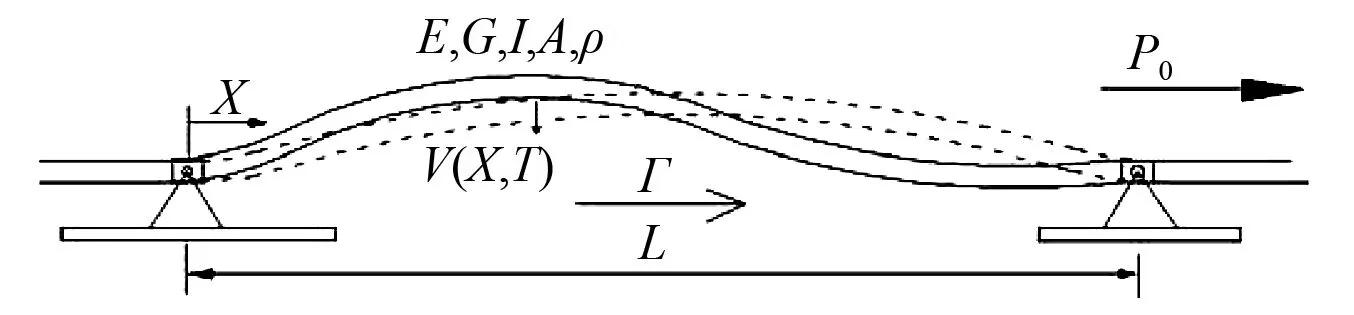
圖1 軸向運(yùn)動(dòng)梁物理模型Fig.1 The physical model of an axially moving beam

根據(jù)廣義的哈密頓原理和Timoshenko梁理論，建立軸向運(yùn)動(dòng)梁的無量綱運(yùn)動(dòng)方程[14-15]

(1)

其中無量綱變量x,t和v(x,t)定義為

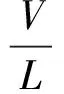
(2)

φ(x,t)為彎矩產(chǎn)生的Timoshenko梁軸線的轉(zhuǎn)角。變量前的逗號(hào)表示求偏導(dǎo)。無量綱參數(shù)定義為

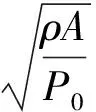
(3)

式中：κ為形狀因子；無量綱參數(shù)k1，k2，kN，kf分別為剪切變形系數(shù)，轉(zhuǎn)動(dòng)慣量系數(shù)，非線性系數(shù)和剛度系數(shù)；ks為軸向支撐剛度參數(shù)。

無量綱簡(jiǎn)支邊界條件為

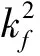
(4)

由于非平凡靜平衡位形與時(shí)間項(xiàng)無關(guān)，因此忽略時(shí)間項(xiàng)得到靜態(tài)控制方程和靜態(tài)簡(jiǎn)支邊界條件

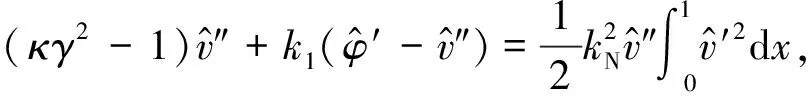
(5)

推導(dǎo)得到簡(jiǎn)支邊界下超臨界下軸向運(yùn)動(dòng)Timoshenko梁的第一階非平凡靜平衡位形

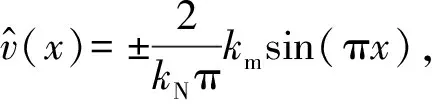
(6)

(7)

2 Galerkin截?cái)?/h2>

對(duì)方程式(1)進(jìn)行坐標(biāo)代換，且只考慮第一階正非平凡靜平衡位形，得到

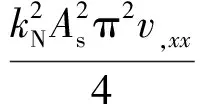
(8)

其中，

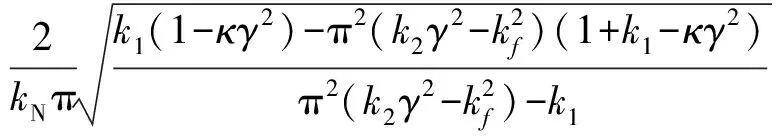
(9)

為滿足兩端簡(jiǎn)支邊界條件，取式(7)形式解[16]如下

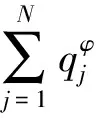
(10)

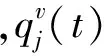
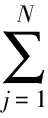
(11)

在式(11)等號(hào)的左右兩邊分別乘以權(quán)函數(shù)sin(iπx)，cos(iπx)，i=1,2,…，N，并在區(qū)間[0,1]上積分，得到常微分方程組

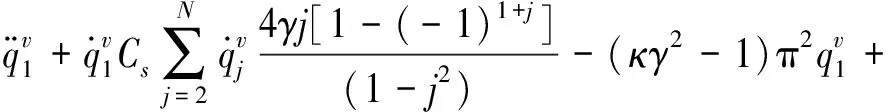
(12)

3 穩(wěn)態(tài)響應(yīng)

運(yùn)用Galerkin截?cái)喾〝?shù)值研究了應(yīng)用于工程實(shí)際中的V型傳動(dòng)帶。

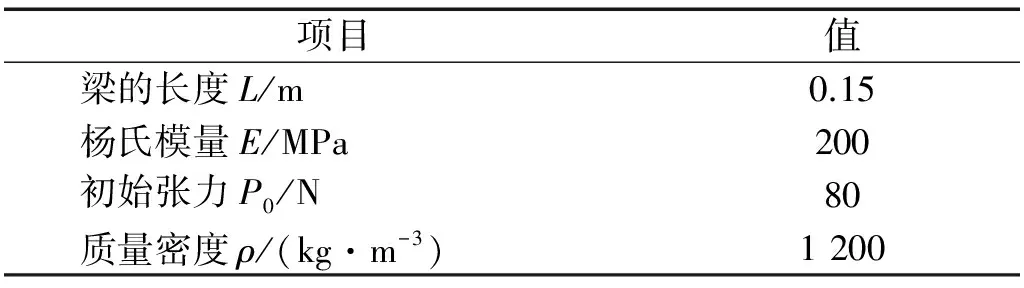
表1 V帶的物理參數(shù)

V帶上底寬為 0.022 m，高為0.018 m，楔角為40°。形狀因子為6/5。外阻尼Cs=0.1。相應(yīng)的無量綱參kf=0.885 6,kN=26.366 3,k1=281.831 4,k2=0.001 1。計(jì)算得到簡(jiǎn)支邊界下超臨界軸向運(yùn)動(dòng)Timoshenko梁的無量綱臨界速度γ=3，相應(yīng)的物理速度Γ=46.45 m/s。

考慮N=4時(shí)的Galerkin截?cái)啵?4，激勵(lì)幅值b=0.000 2，運(yùn)用四階龍格-庫(kù)塔法計(jì)算激勵(lì)頻率接近系統(tǒng)第一階固有頻率時(shí)，式(12)的響應(yīng)。仿真中，時(shí)間步長(zhǎng)取0.01 s，初始條件取為0。在計(jì)算所得的前500 s的時(shí)間歷程中，取最后5 s計(jì)算Timoshenko梁的穩(wěn)態(tài)幅頻響應(yīng)[17]。

如圖2所示為超臨界軸向運(yùn)動(dòng)Timoshenko梁橫向受迫振動(dòng)前500 s的時(shí)間歷程。

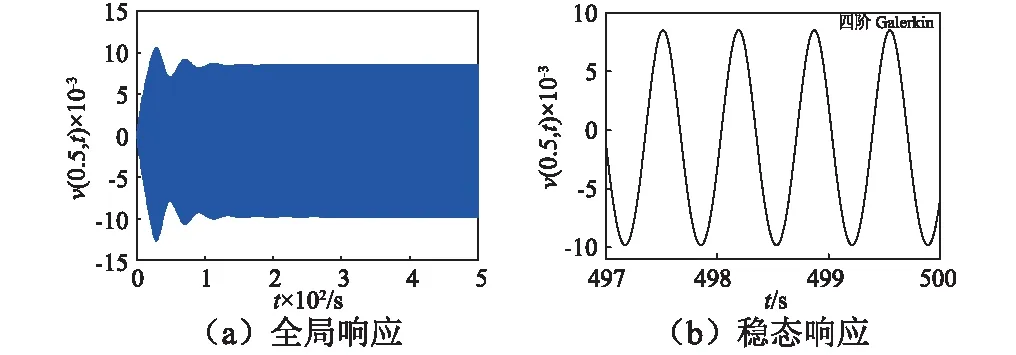
圖2 橫向受迫振動(dòng)時(shí)域響應(yīng)(ω=9.25)Fig.2 Time-domain response of lateral forced vibration

考慮四階Galerkin截?cái)嘤?jì)算梁中點(diǎn)的穩(wěn)態(tài)振幅，研究第一階主諧波共振時(shí)的穩(wěn)態(tài)響應(yīng)。圖3～圖5分別給出了剪切變形系數(shù)、轉(zhuǎn)動(dòng)慣量系數(shù)和外阻尼對(duì)第一階主諧波共振時(shí)穩(wěn)態(tài)幅頻特性曲線的影響。圖3表明共振幅度隨剪切變形系數(shù)的增大而增大，幅頻特性曲線向左偏，呈現(xiàn)軟特性，且隨著剪切系數(shù)的增大，軟特性增強(qiáng)。圖4表明共振幅度隨剪切變形系數(shù)的增大而減小，軟特性減弱。圖5表明共振幅度隨外阻尼的增大而減小，軟特性減弱。

4 與Euler-Bernoulli梁理論對(duì)比

超臨界軸向運(yùn)動(dòng)Euler-Bernoulli梁橫向受迫振動(dòng)控制方程

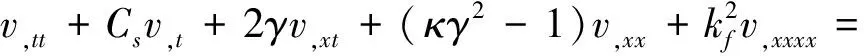
(13)

圖3 剪切變形系數(shù)對(duì)穩(wěn)態(tài)幅頻特性曲線的影響Fig.3 Effects of shear deformation coefficient of amplitude frequency response

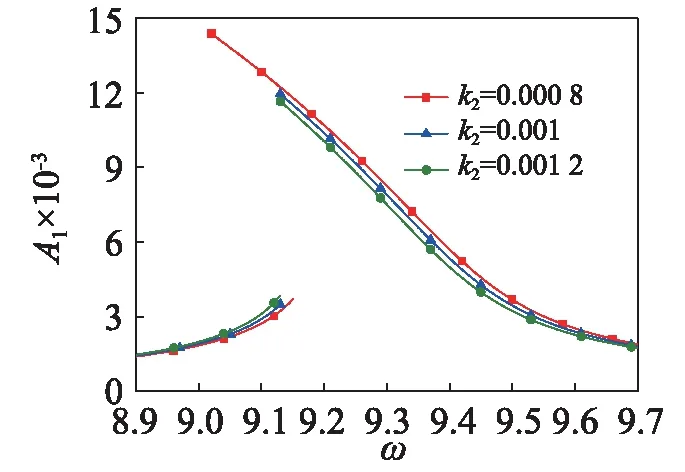
圖4 轉(zhuǎn)動(dòng)慣量系數(shù)對(duì)穩(wěn)態(tài)幅頻特性曲線的影響Fig.4 Effects of rotary inertia coefficient of amplitude frequency response

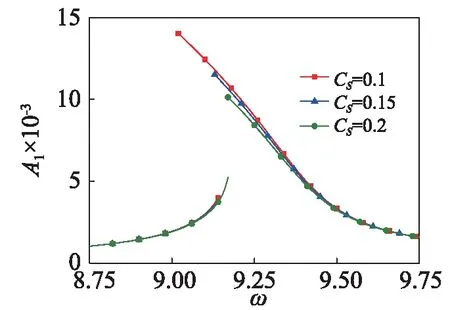
圖5 外部阻尼對(duì)穩(wěn)態(tài)幅頻特性曲線的影響Fig.5 Effects of external damping of amplitude frequency response

簡(jiǎn)支邊界下E-B梁第一階非平凡靜平衡位形

(14)

對(duì)式(12)進(jìn)行坐標(biāo)代換，且只考慮E-B梁的第一階正非平凡靜平衡位形，得到

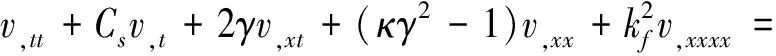
(15)

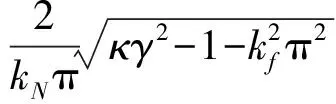
(16)

為滿足兩端簡(jiǎn)支邊界條件，取式(17)為式(14)的形式解

(17)

將式(16)代入式(14)后，在方程兩邊同乘以權(quán)函數(shù)sin(iπx)，i=1,2,…，N，并在區(qū)間[0,1]上積分，得到常微分方程組

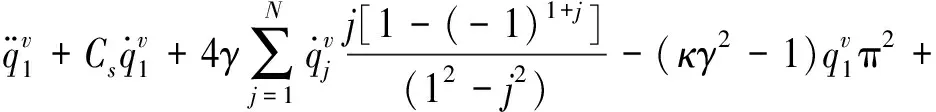
(18)

圖6和圖7分別給出了不同梁模型下梁長(zhǎng)和梁橫截面高度對(duì)穩(wěn)態(tài)響應(yīng)幅頻特性曲線的影響。

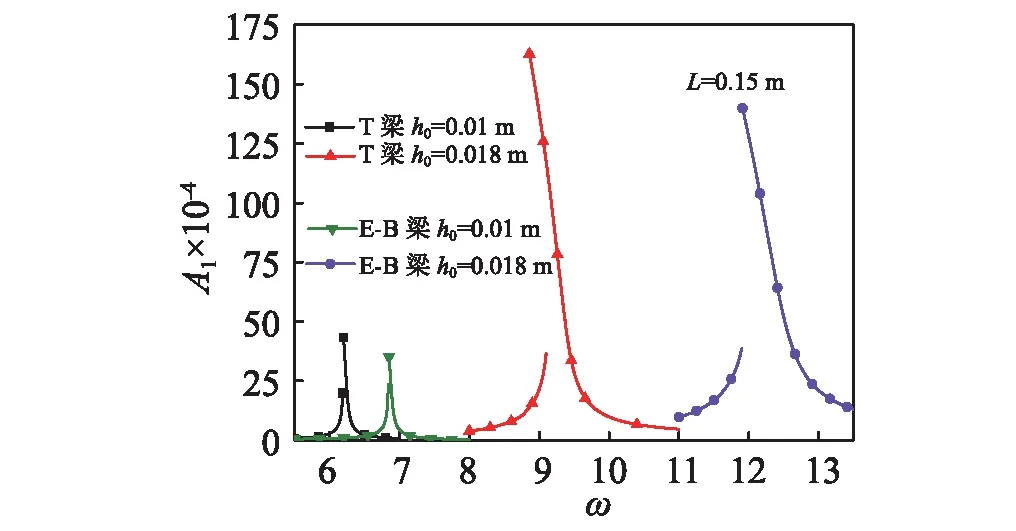
圖6 梁橫截面高度對(duì)穩(wěn)態(tài)幅頻特性曲線的影響Fig.6 Effects of beam cross section height of amplitude frequency response

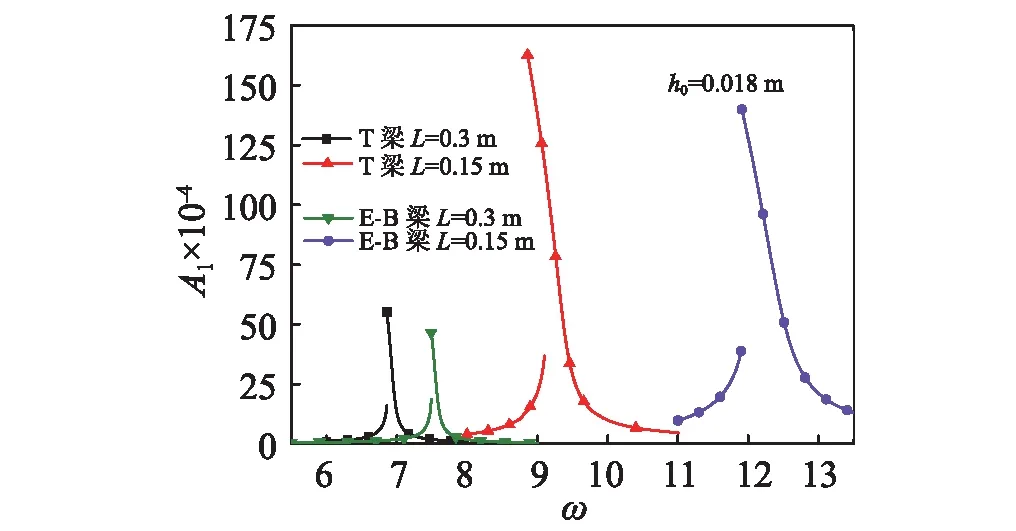
圖7 梁長(zhǎng)對(duì)穩(wěn)態(tài)幅頻特性曲線的影響Fig.7 Effects of beam length of amplitude frequency response

圖6中考慮了兩種梁模型橫截面高分別為0.01 m和0.018 m時(shí)的穩(wěn)態(tài)響應(yīng)幅頻特性曲線，從圖6可知，兩種梁模型的共振頻率差別較大，共振幅度也有較大差別。圖7考慮了兩種梁模型梁長(zhǎng)分別為0.15 m和0.3 m時(shí)的穩(wěn)態(tài)響應(yīng)幅頻特性曲線，同樣，兩種梁模型的共振頻率差別較大，共振幅度也有較大差別。從圖6和圖7可知，當(dāng)L與h0的比值變大時(shí),兩種梁模型之間的差別變小。

5 結(jié) 論

本文運(yùn)用Galerkin截?cái)喾〝?shù)值研究了有外阻尼的超臨界軸向運(yùn)動(dòng)Timoshenko梁的橫向受迫振動(dòng)，得到了Timoshenko梁穩(wěn)態(tài)周期幅頻特性曲線，并考慮了相關(guān)參數(shù)對(duì)其的影響。

同時(shí)對(duì)比了Timoshenko和Euler-Bernoulli這兩種梁模型在超臨界軸向速度下的穩(wěn)態(tài)幅頻特性曲線，發(fā)現(xiàn)兩種梁模型的幅頻特性曲線存在較大差別，當(dāng)梁的截面高度變大時(shí)，兩種梁模型的穩(wěn)態(tài)幅頻特性曲線差別變大，當(dāng)梁長(zhǎng)變大時(shí)，兩種梁模型的穩(wěn)態(tài)幅頻特性曲線差別變小。

[ 1 ] WICKET J A, MOTE C D. Classical vibration analysis of axially moving continua [J]. ASME Journal of Applied Mechanics, 1990, 57 (3)： 738-744.

[ 2 ] ZHU W D. Vibration and stability of time-dependent of translating media [J]. Shock and Vibration Digest, 2000, 32 (5): 369-379.

[ 3 ] CHEN L Q. Analysis and control of transverse vibration of axially moving strings [J]. ASME Applied Mechanics Reviews, 2005, 58 (2): 91-116.

[ 4 ] MARYNOWSKI K, KAPITANIAK T. Dynamics of axially moving continua [J]. International Journal of Mechanical Sciences, 2014,81(4): 26-41.

[ 5 ] 宮蘇梅, 張偉. 平帶系統(tǒng)非線性振動(dòng)實(shí)驗(yàn)研究[J]. 動(dòng)力學(xué)與控制學(xué)報(bào), 2014, 12(4): 368-372.

GONG Sumei, ZHANG Wei. Experimental study on nonlinear vibration of flat-belt system[J]. Journal of Dynamics and Control, 2014, 12(4): 368-372.

[ 6 ] 呂海煒, 李映輝, 李亮, 等. 軸向運(yùn)動(dòng)軟夾層梁橫向振動(dòng)分析[J]. 振動(dòng)與沖擊, 2014, 33(2): 41-51.

Lü Haiwei, LI Yinghui, LI Liang, et al. Analysis of transverse vibration of axially moving soft sandwich beam[J]. Journal of Vibration and Shock, 2014, 33(2): 41-51.

[ 7 ] 丁虎, 陳立群. 軸向運(yùn)動(dòng)黏彈性梁橫向非線性受迫振動(dòng)[J]. 振動(dòng)與沖擊, 2009, 28(12): 128-131.

DING Hu, CHEN Liqun. Transverse non-linear forced vibration of axially moving viscoelastic beam[J]. Journal of Vibration and Shock, 2009, 28(12): 128-131.

[ 8 ] DING H, CHEN L Q. Natural frequencies of nonlinear vibration of axially moving beams[J]. Nonlinear Dynamics, 2011, 63(1/2): 125-134.

[ 9 ] GHAYESH M H, KHADEM S E. Rotary inertia and temperature effects on non-linear vibration, steady-state response and stability of an axially moving beam with time-dependent velocity [J]. International Journal of Mechanical Science, 2008, 50 (3): 389-404.

[10] HUANG S J, PERKINS N C. Supercritical stability of an axially moving beam. Part Ⅱ: vibration and stability analyses [J]. Journal of Sound and Vibration, 1992, 154 (3): 397-409.

[11] DING H, CHEN L Q. Galerkin methods for natural frequencies of high-speed axially moving beams [J]. Journal of Sound and Vibration, 2001, 329 (17): 3484-3494.

[12] TANG Y Q, CHEN L Q, YANG X D. Non-linear vibrations of axially moving Timoshenko beams under weak and strong external excitations [J]. Journal of Sound and Vibration, 2009, 320 (4/5): 1078-1099.

[13] YAN Qiaoyun, DING Hu, CHEN Liqun. Nonlinear dynamics of an axially moving viscoelastic Timoshenko beam under parametric and external excitations[J].Applied Mathematics and Mechanics (English Edition), 2015, 36(8): 971-984.

[14] DING H, JEAN W Z. Effect of one-way clutch on the nonlinear vibration of belt-drive systems with a continuous belt model[J]. Journal of Sound and Vibration, 2013, 332(24): 6472-6487.

[15] YAN Q Y, DING H, CHEN L Q. Periodic responses and chaos behaviors of an axially accelerating viscoelastic Timoshenko beam[J]. Non-linear Dynamics, 2014, 78(2):1577-1591.

[16] CHEN S H, HUANG J L, SZE K Y. Multidimensional Lindstedt-Poincaré method for nonlinear vibration of axially moving beams[J]. Journal of Sound and Vibration, 2007, 306(1/2): 1-11.

[17] 李大鵬, 儲(chǔ)德林, 丁虎. 輪-帶驅(qū)動(dòng)系統(tǒng)穩(wěn)態(tài)周期響應(yīng)諧波平衡分析[J]. 動(dòng)力學(xué)與控制學(xué)報(bào), 2015, 13(6): 423-429.

LI Dapeng, CHU Delin, DING Hu. The frequency-response curve of a belt-drive system by using the harmonic balance method[J]. Journal of Dynamics and Control, 2015, 13(6): 423-429.

TransverseforcedvibrationofanaxiallymovingTimoshenkobeamatasupercriticalspeed

TAN Xia1, DING Hu1, CHEN Liqun1,2

(1. Shanghai Institute of Applied Mathematics and Mechanics, Shanghai University, Shanghai 200072, China;2．College of Sciences, Shanghai University, Shanghai 200444, China)

In this paper, the transverse nonlinear forced vibration of an axially moving Timoshenko beam at a supercritical speed was studied under external excitation. In the supercritical region, the standard control equation of the gyro system, under the lateral external incentives, was derived based on the governing equation of transverse nonlinear vibration of the axially moving Timoshenko beam. Moreover, the steady-state amplitude frequency response relationship of the axially moving Timoshenko beam at a supercritical speed was investigated by using the Galerkin method. Furthermore, the effects of system parameters on the steady-state amplitude frequency response relationship of the Timoshenko beam were considered. Comparisons with Euler-Bernoulli (E-B) beam reveal that the resonance frequency of the Timoshenko beam is much lower and the resonance amplitude is higher in the supercritical region.

supercritical; axially moving beam; Timoshenko theory; forced vibration; Galerkin method

國(guó)家自然科學(xué)基金重點(diǎn)項(xiàng)目(11232009); 國(guó)家自然科學(xué)基金項(xiàng)目(11372171; 11422214)

2016-06-02 修改稿收到日期： 2016-09-28

譚霞 女，碩士生，1992年生

丁虎 男，博士，教授，博士生導(dǎo)師，1978年生

E-mail: dinghu3@shu.edu.cn

O322

A

10.13465/j.cnki.jvs.2017.22.001