淺談對數學“傳知”和“育人”功能的理解

潘秋梅

深圳市第一職業技術學校

淺談對數學“傳知”和“育人”功能的理解

潘秋梅

深圳市第一職業技術學校

數學時刻存在于我們的生活中，從幼兒園開始，數學就以一門學科的形式，成為我們學習的重要部分。那么，在數學的教學中，我們應該教給孩子什么？僅僅是知識？思維？還是有其他的方面？本文圍繞“數學要教給孩子什么”這個問題展開，結合高中數學的具體例子，闡述了數學“傳知”和“育人”功能的理解。

教育；教學；傳知；育人

在一份關于“幼兒教育”的雜志里面有兩個關于這樣的實例：例1，一個叫丁丁的小朋友，在老師的指導下，用5元錢象征性的去購買東西。這個小朋友購買了一個標價為2元的蘋果和一盒標價為3元的餅干，就把錢給花完了。然后老師讓學生寫一個算術式，丁丁寫：2＋3＝0。老師說丁丁寫錯了，丁丁說沒有錯。確實沒有錯呀，因為5元錢嘛，花完了，當然等于零了。例2，一個叫漸漸的朋友，在一個數學教研員對他進行訪問時，問他3＋7＝？，漸漸馬上回答等于10。然后又再問為什么呢？漸漸說，就是等于10，不為什么。后來無論這個數學教研員怎么引導和啟發，漸漸依然回答等于10 。最后問急了，漸漸干脆說，就是等于10，不等于10就是錯的。

看了這兩個例子，我開始了思考：數學到底要教給孩子什么？數學教學應該具有什么功能？

數學教育作為學校教育的重要組成部分，以它獨特的風格，承擔著“傳知”和“育人”的任務。“傳知”即傳承人類主流、基礎性的數學知識、方法、精神、文化等；“育人”即訓練與培養受教育者學習規則、運用規則、發現結構與規律，探求解答的“處理數據、信息，進行計算和推理”的采集、解讀信息、推演、表達信息和驗證信息的能力與素質。

首先，談談對數學的“傳知”功能的理解。數學是客觀物質世界的數量關系及空間形式的客觀規律的反映，它本身具有結論明確的特點。而數學課是學校教育的基礎課之一，數學教育是一種文化基礎教育。因此，它承擔著傳播文化、繼承知識、發展知識的使命。

在數學教學當中，特別是某些定理的證明推導過程中，學生經常會問：老師，我們學這些有什么用？我們根本用不上。是的，很多的數學知識，在我們的日常生活中不經常用，例如微積分、線性規劃、向量、平面解析幾何等，這些知識一般只在科技領域、發明領域等先進領域才用到，換一句話來說，這些知識是為科學家和發明家們準備的。

數學是一門最活躍、充滿哲理、密切聯系實際的學科，數學教學還具有其他學科無法替代的德育功能，通過數學的教學可培養和提高人的許多非智力品質，在育人中發揮積極作用。一般來說，數學的“育人”功能包括：教會學生數學認知功能、運算功能、應用功能、思維功能等等。下面通過一個數學實例來談談我對數學教學怎樣實現它的這一功能的認識。

已知點P0(x0, y0)和直線l：Ax+By+C=0，求證點P0(x0, y0)到直線l的距離(也就是點到直線的距離公式的推導)

一、學生審題，對信息進行采集：已知一點P0(x0, y0)，直線方程為Ax+By+C=0，求點P0(x0, y0)到直線的距離d。學生在審題的這一過程中，就經歷了對信息的概括與簡要分析，概括能力與辨別能力得到鍛煉與發展。

二、學生進行信息解讀：對采集出來的信息，似乎很抽象，那么很多學生會嘗試作圖幫助理解題意，從而尋求解題方法。在解讀信息的過程中，學生經歷了思維方式的一個轉換，進入到數形結合分析。過點P0(x0, y0)作直線l的垂線，垂足設為Q，即d=|P0Q|，已知點P0的坐標，若知道點Q的坐標，根據兩點距離公式：若A(x1, y1)，B(x2, y2)則，就可以求出點到直線距離d。Q的坐標怎樣求？Q是直線l和直線P0Q的交點，而要求交點，就必須要知道P0Q的直線，由于P0Q和l垂直，根據兩條垂直直線的關系：與直線Ax+By+C=0垂直的直線方程為Bx-Ay+D=0可求。分析完這些，進入具體的推導過程，發現此方法雖然思路直觀，但運算非常繁雜。

于是可以尋找另外一種運算較為簡單的方法。要想求距離d，還可以通過構造直角三角形，根據同一三角形面積相等，可求高d。于是通過作圖構造直角三角形：過P0作x軸的垂線，交直線l于點F，過P0作y軸的垂線，交直線l于點E。由題意可設點E(x1, y0)，F(x0, y2)。

學生在這一過程中，經歷了分析、綜合、比較的思維過程，提高了分析問題與解決問題的能力，這對學生在日常生活中遇到矛盾、解決矛盾方面準備了思維方式，雖然在日常生活中，這種引導沒有表現得那么明顯，但時刻在影響我們的判斷與處理能力。

三、解答過程：

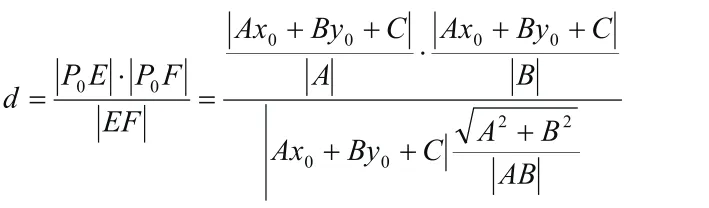
在解答的這一過程中，學生經歷了整理、推導的過程，在繁雜的運算中，訓練了思維的清晰度與條理性，另一方面，培養了學生的耐心與恒心，同時，學生還能從中獲得成功的喜悅，增強信心。

在數學教學中，還可以體現數學中的運動變化、矛盾轉化、量變到質變、普遍聯系等辯證法思想，反映數學源于實踐又反作用于實踐的認識論觀點，還能倡導和培養學生具有實事求是、勇于創新、嚴謹踏實的科學態度，具有頑強學習和戰勝困難的堅強意志，具有周密細致分析問題和創新解決問題的邏輯思維，具有善于獨立思考又善于協作學習的精神、具有欣賞美和創造美的美學修養等數學品質，數學，基在“傳知”，重在“育人”。

[1] 鄧小榮.高中數學的體驗教學法[J].廣西師范學院學報.2003(8)

[2] 中華人民共和國教育部制定.普通高中數學課程標準(實驗稿)[M].北京：北京師范大學出版社，2003.