粘性流體數值波浪水池研究

高 慧，張照剛，熊高涵

(江蘇科技大學 船舶與建筑工程學院，江蘇 張家港 215600)

粘性流體數值波浪水池研究

高 慧，張照剛，熊高涵

(江蘇科技大學 船舶與建筑工程學院，江蘇 張家港 215600)

數值波浪水池是近年來船舶流體力學方向的前沿課題，本文采用Fluent軟件，利用VOF模型捕捉自由液面，結合湍流模型，求解N-S方程，對目前數值造波較為典型的仿物理造波法和直接造波法在二維模式下進行分析，并對三維模式的數值造波作了初步分析。在仿物理造波法中模擬真實水池中推板式造波機，利用動網格和阻尼消波技術，生成規則波的情況。在直接造波法中，利用給定入口邊界速度或壓力并結合阻尼消波技術，在數值水池模擬規則波，得到直接造波法的數值波形與理論波形的吻合度要優于仿物理造波法的結果。為在數值波浪水池中對船舶水動力性能預報奠定基礎。

數值造波；規則波；動網格；VOF模型

0 引 言

物理波浪水池是船舶流體力學研究的重要試驗設施，為船舶水動力性能研究提供高效而又可靠的實驗數據，但是物理波浪水池花費時間和費用多，實驗周期長，在非規則波的模擬以及消波上還存在許多問題[1]。隨著計算機技術的飛速發展，用數值模擬波浪及波浪與船舶的相互作用變成了可能。數值波浪水池在造波和消波方面具有物理波浪水池不具有的優勢。采用基于波浪理論的方法進行造波和消波，可以獲得詳細的流場信息。

本文基于Fluent軟件建立了二維數值波浪水池，分別采用仿物理造波法和直接輸入造波法模擬了無限水深條件下的規則波，并將由2種方法得到的波浪與理論值進行對比，分析了各種方法的特點，并擴展到三維情況，采用直接輸入法造波，得到了滿足要求的規則波。

1 數值水池的原理

對于規則波，采用仿物理造波法時，模擬真實水池中推板式造波機，往復推板在水池中作正弦運動，運動軌跡及速度方程[2]如下：

由線性造波理論可知：生成波浪的波面方程和速度勢為：

圖1為仿物理造波法的數值波浪水池。水池左邊界為模擬推板的動邊界，式（2）表示為運動邊界的速度方程。采用Fluent自帶UDF編程，造波板按式（1）表示的軌跡運動，速度按式（2）。一旦造波板的運動頻率和行程確定以后，即可以獲得相應頻率和波高的規則波。圖1中右邊界為消波區，波浪進入該區域以后將逐漸衰減，最終趨于平靜[3]。

采用直接輸入法造波需要在入口邊界上給定流體的速度或壓力，模擬波浪的速度場或壓力場，該方法原理簡單，消耗機時較少，數值波浪水池如圖2所示。

對于規則波的模擬，根據波浪理論，可得到相應波浪的速度場，由線性假設，無限水深條件下，規則波的波面方程可表示為：

速度勢：

色散關系：

規則波的速度場：

壓力場：

式中：k為波數，ω為波浪圓頻率，a為波幅，x軸為波浪傳播方向，z軸為波動方向，p0為大氣壓強，z軸自由液面以下取負值。

將規則波質點的速度表達式（8）作為數值水池入口邊界條件，用UDF編程定義入口邊界水平和垂向的波浪速度函數。

為了防止波浪反射對計算域的影響，在下游設置消波區。數值波浪水池中常采用的消波技術-阻尼消波區。

阻尼消波區是在特定的自由邊界加入人工粘性項，對流體質點的垂向速度做強制衰減，通過對消波區網格沿波浪傳播方向逐漸變稀，增加阻尼，達到快速消波的目的[4]。為了保證計算域內流動的連續性，在水平方向的速度不做衰減[5]。

人工阻尼系數如式（10）所示：

則消波區波動方向的速度為：

式中：α為阻尼控制參數；下標s為消波區的起點，e為消波區的終點；b為底部；fs為自由面；w為流體質點在波動方向的速度。

在消波段的動量方程中加入阻尼項，如下式：

式中：γ為消波系數；μ為動力粘性系數。

對γ的確定，要考慮使消波區內流體的運動滿足連續性方程。Laesen和Dancy給出了消波系數[6]：

式中：xs為消波區的長度；Δx為消波區的網格尺寸；α為常數。

2 數值模擬方法

2.1 計算域和網格劃分

首先采用仿物理造波法模擬規則波，數值波浪水池模型尺寸為30×8 m，其中水深5 m，消波區長10 m。數值水池網格劃分如圖3所示；在自由液面附近加密網格，利于捕捉自由液面，距出口邊界10 m處將計算域分為2個分區，后部分區中網格沿波浪傳播方向，網格逐漸變稀，稀疏的網格增加了額外的阻尼，利于消波。

2.2 兩相流模型

采用氣液兩相流模型，非定常分離隱式求解器求解離散方程組。選擇RNG k -ε湍流模型，該模型最早由Yakhot和Orzag提出，是一種對瞬時的N-S方程用重整化的方法推導出來的湍流模型，目前在船舶工程領域應用較為廣泛。與其他湍流模型相比，RNG k -ε湍流模型針對充分發展的湍流有效，具有更強的適應性。

自由液面用VOF方法捕捉，壓力速度耦合方程用PISO算法。定義左側邊界為造波推板其運動速度隨時間變化如式（2），網格的更新采用動網格重構法。

2.3 邊界條件

仿物理造波法，在計算域的邊界上采用下列邊界條件：左端、下端和上端邊界設為無滑移壁面，右端為靜壓力出口；水池采用壁面邊界條件。由于流動非定常，設定初始速度為0。直接輸入法邊界條件除左端為速度入口邊界外其余和仿物理造波法相同。

2.4 計算結果和分析

圖4為t=14.3s時數值波浪水池的波形圖。為測量數值水池中波浪隨時間的變化，在4 m的位置設置浪高儀。圖5為4 m處波幅的時歷曲線與理論波形的比較。

從圖5中可看出仿物理造波法波形與理論波形總體上吻合，但存在30°左右的相位差，而且波幅低于理論波形，這主要是由造波推板以及流體的粘性的影響造成的。采用直接輸入法得到的波浪，波形與理論波形兩者之間存在大約15°左右的相位差，且波高小于理論值，這主要是由于流體的粘性使得波浪在傳播過程中逐漸衰減造成的，與實際情況相符。表1和表2給出了與理論波形相比數值波形的波幅及周期的相對誤差。

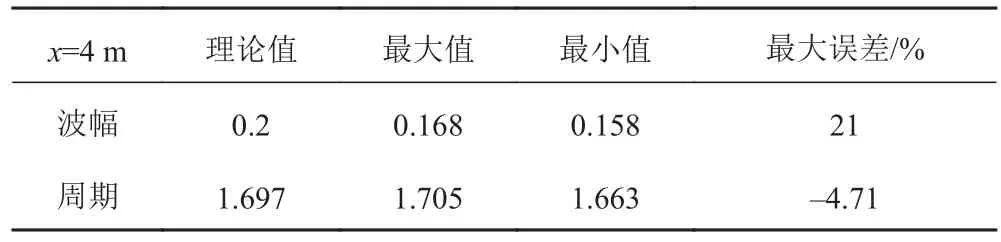
表 1 二維數值波形與理論值的誤差對照表（仿物理造波法）Tab. 1 Error comparison between two dimensional numericalwaveform and theoretical value (physics simulation of the wave-making method)

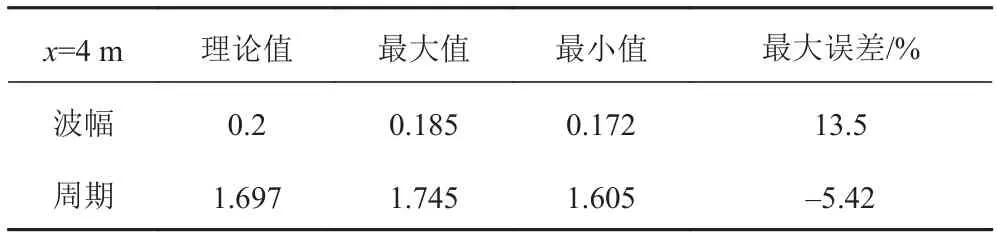
表 2 二維數值波形與理論值的誤差對照表（直接輸入法）Tab. 2 Error comparison between two dimensional numerical waveform and theoretical value (direct Wave-making method)

對比2種方法得到的波形，直接輸入法的波形與理論波形吻合度更好，同時考慮到仿物理造波法存在動網格重構、計算時間長等因素及推板對流場的影響。而直接輸入法，只要設定波動速度入口，對流場不會產生影響。故采用直接輸入法預報波浪中的船舶水動力性能更有優勢。

將二維數值波浪水池中的直接輸入造波法和消波技術應用到三維數值波浪水池中。三維數值波浪水池的計算域、邊界條件及控制參數和二維數值波浪水池相近。波形圖如圖6所示。

圖7為4 m處三維數值波浪水池和二維數值波浪水池中的波形與理論波形的比較。通過比較可知三維波形與理論波形吻合度最好。但是三維波形達到穩定需要的時間更長，二維波形在6 s時基本穩定，而三維波形則要到8.1 s以后才穩定。三維波形波高的衰減要比二維數值波浪水池小很多，由表3可知，4 m處三維數值波浪水池中波幅與理論波幅相比最大誤差為-5.5%，遠低于二維數值水池，且三維波形的周期更接近理論周期，與理論波形吻合的程度要優于二維數值波浪水池。

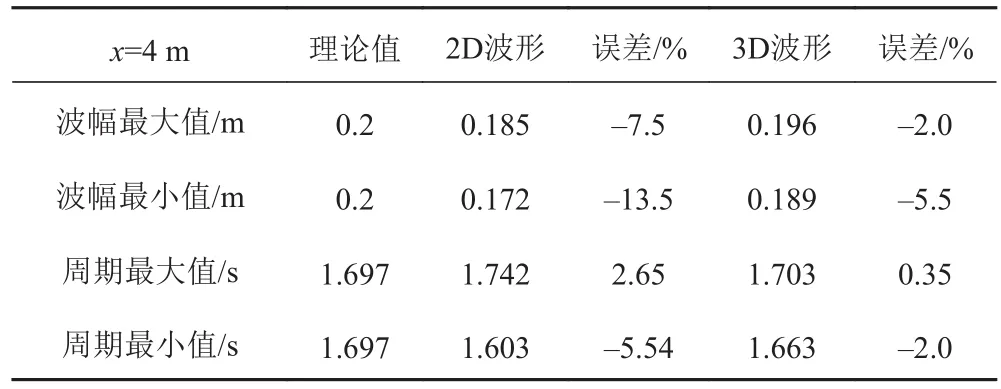
表 3 三維數值波形與理論值的誤差對照表Tab. 3 Error comparison between three dimensional numerical waveform and theoretical value

3 結 語

1）通過對2種造波方法所得到的數值波形進行對比，直接輸入法簡單易懂，誤差較小，且沒有造波板對流場的干擾，可更快得到穩定的規則波，節省計算機時間。

2）在數值波浪水池下游加入消波區，采用人工阻尼法消波，消波區水面逐漸趨于平靜，在水池出口處已基本不存在波動，說明人工阻尼法用于規則波的消波可行。

3）由RNG kk --εε湍流模型獲得的波高值在水池的長度方向上有一定的衰減，這主要是由于RNG k -ε湍流模型考慮了流體的粘性作用而導致的。

4）通過計算直接輸入法造波的二維與三維數值波浪水池可知，直接輸入法用于三維數值波浪水池造波所得到的波形與理論波形相比誤差要小于二維數值波浪水池。

[1]張亞群. 造波機的控制及其實現[D]. 武漢: 武漢理工大學.2007.

[2]鄒志利. 水波理論及其應用[M]. 北京: 科學出版社, 2005.

[3]JOUMEE J M J. Experiments and calculations on 4 Wighy hull forms in head waves[R]. Report of Delft University of Technology, Ship Hydromechanics Laboratory, The Netherlands, 1992.

[4]吳乘勝, 周德才, 蘭波, 等. 高速三體船波浪中運動與增阻CFD計算研究[J]. 船舶力學, 2010, 51(4): 1-10.

[5]方昭昭, 朱仁傳, 繆國平. 數值波浪水池中航行船舶輻射問題的數值模擬[J]. 水動力學研究與進展, 2011, 26(1) 66-72.

[6]郭海強. 船舶性能數值水池的研究及其若干應用[D]. 上海: 上海交通大學, 2009.

Study of numerical wave tank for viscous fluid

GAO Hui, ZHANG Zhao-gang, XIONG Gao-han
(Jiangsu University of Science and Technology, Zhangjiagang 215600, China)

Numerical wave basin is a frontier subject in the direction of fluid mechanics in recent years.In this paper,the N-S equation was resolved by the VOF model to capture the free surface, combined with theturbulence model using the Fluent software. At present, the typical model of the physics simulation of the wave-making method and the direct wave-making method is analyzed, and aslo the three-dimensional numerical wave-making was analyzed as an introduction .In the simulation of the physics wave-making, simulate the rocker-flap wave maker in the real tank. The simulation,using the moving grid and damping wave elimination technique to make the regular wave. In the direct wave making method, using the given inlet boundary velocity or pressure and combined with the damping wave elimination technique, the numerical simulation rules, the results of the numerical waveform and the theoretical waveform of the direct wave makingmethod are better than the results of the physics simulating wave method.

numerical wave-makting；regular wave；dynamic mesh；VOF model

U661.43

A

1672-7649(2017)11-0044-04

10.3404/j.issn.1672-7649.2017.11.009

2016-10-12；

2016-11-03

高慧(1981-)，男，碩士，實驗師，研究方向為船舶流體力學。