基于多慣性傳感器姿態的輸電線舞動監測算法研究

朱勤翔， 郭 薇， 張 港

(上海交通大學 區域光纖通信網與新型光通信系統國家重點實驗室，上海 201100)

基于多慣性傳感器姿態的輸電線舞動監測算法研究

朱勤翔， 郭 薇， 張 港

(上海交通大學區域光纖通信網與新型光通信系統國家重點實驗室，上海201100)

針對目前使用慣性(MARG)傳感器還原輸電線舞動形狀存在很多原理性的問題，如位置積分起始點未知、容易丟失輸電線低頻運動信息等,提出了一種基于慣性傳感器姿態的輸電線舞動形狀還原算法，采用融合同一根輸電線上多個MARG的姿態求取每個MARG真實位移以及輸電線整體形狀。算法能夠避免加速度積分時的累積誤差，解決了輸電線長度約束問題且使用較少MARG即可還原舞動圖像。仿真結果表明：算法可以有效地降低導線舞動振幅的誤差，且還原誤差不隨時間增長。

慣性傳感器； 姿態—曲線還原算法； 輸電線舞動； 姿態

0 引 言

輸電線在覆冰條件下受到強風的激勵，容易產生一種自激的、低頻、振幅巨大的無規則舞動，從而引起輸電線脫皮、跳閘、斷股、甚至拉倒桿塔等危害[1]。常用的基于加速度的舞動監測系統在一根輸電線上綁定多個慣性傳感器(MARG)并測量其加速度、地磁場以及角速度，然后對校正后的MARG加速度進行二次積分得到位移信息,最后通過插值得到整根輸電線形狀[2]。

該系統存在以下問題： 1)加速度積分過程中，初始速度值和位置值無法準確估計。2)在積分過程中，由于要解決噪聲引起的積分不收斂，一般均需要加入濾波器消除噪聲。而濾波器消除了真實的MARG的低頻移動。因此，即使速度和位置的初始值足夠準確，經過一段時間后系統仍然無法計算MARG的準確位移。3)由于每個MARG得到的位移均不夠精確，綜合這些位移擬合得到的輸電線的整體形狀與真實值有較大誤差。4)剛體繞著某個軸做某個角度的旋轉后得到的角度關系稱為該剛體的姿態，監測系統需要計算MARG姿態以消除轉動誤差。在經典的姿態算法中一般需要加速度計、陀螺儀和磁力計三種傳感器同時使用才能獲得準確的姿態[3]。但在基于加速度的監測系統中加速度用于積分位移，因此，只能使用另外兩者計算姿態[2]，最終會導致校正過的加速度仍然不準確。

針對上述問題，本文提出了一種新的基于傳感器姿態的輸電線舞動監測系統及姿態—曲線還原算法。算法舍棄了加速度積分的原理，通過計算綁定在輸電線上的MARG的姿態，再結合MARG的綁定位置得到整根輸電線的形狀。仿真及實驗結果表明：本文方法能夠很好地避免現有系統的缺陷，并且可以有效地提高還原的位移精度，從而獲得較為精確的整體輸電線舞動形狀。

1 基于姿態舞動監測系統及還原算法

1.1 基于姿態舞動監測系統

圖1所示，多個MARG測量單元綁定于同一根輸電線:兩端各綁定一個MARG，其余以等間隔綁定在輸電線中央。每個MARG內含有加速度計、磁力計和陀螺儀用于測量其姿態。基于姿態的監測系統與現有基于加速度的監測系統硬件結構相同，包括帶有無線傳輸功能的MARG、監測基站以及遠程控制中心[4]。基于姿態的舞動監測系統的數據處理流程為：接收MARG的測量數據后，系統首先使用姿態算法計算MARG的實時姿態[3，5]，其次使用姿態—曲線還原算法得到整根輸電線形狀，最后計算其他舞動參數，如舞動頻率等。

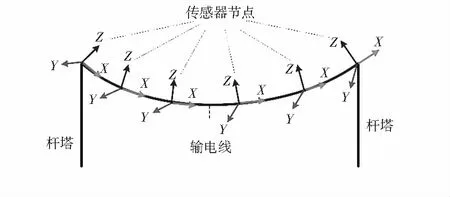
圖1 基于姿態舞動監測系統示意

1.2 姿態曲線還原算法

1.2.1 建立輸電線方程

姿態—曲線還原算法使用MARG實時姿態作為輸入，并通過其計算整根輸電線的實時形狀。根據MARG的姿態可以計算綁定點輸電線的切線方向，且相鄰MARG之間的輸電線長度為一個已知的常數。姿態—曲線還原算法中用于描述輸電線的曲線方程必須具有以下4個性質：

1)連續性約束：曲線必須處處連續，在綁定MARG的“測量點”上也必須連續。

2)首尾位置約束：曲線的起點和終點必須和輸電線的首尾兩端的坐標相同。

3)切線約束：曲線在測量點上的切線方向必須與實際MARG測量的切線方向相同。

4)弧長約束：該曲線在相鄰測量點間的曲線長度必須等于原輸電線在對應測量點間的弧長。

為滿足上述4個約束，姿態—曲線還原算法使用空間曲線r(t)=(x(t),y(t),z(t))作為描述輸電線的方程[6，7]。該曲線的導數r′(t)=(x′(t),y′(t),z′(t))等于某個二次函數σ(t)(空間曲線的速度)

x′2(t)+y′2(t)+z′2(t)=σ2(t)

(1)

該曲線的導數有另外一種等價的復數形式[6]

r′(t)=(|α(t)|2-|β(t)|2,

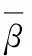
(2)

σ(t)=|α(t)|2+|β(t)|2

(3)

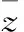
為了滿足MARG所處測量點的切線約束以及弧長約束，姿態—曲線算法對每一段被測量點分割的輸電線均使用獨立曲線表示。具體地，如果一條輸電線上綁定了n+1個MARG，那么該輸電線將被分成n段，姿態—曲線還原算法使用n段曲線來表示各段輸電線。而每一段的曲線方程ri(t)的α(t),β(t) 系數表示為

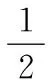
(4)

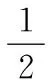
(5)

式中 (pi,qi),i=0,…,N+1為n+2組復數常數；t的取值范圍為t∈[0,1]。由上文中4個約束知曲線簇必須滿足約束方程

ri(1)=ri+1(0),i=1,…,N-1

(6)

(7)

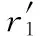
i=1,…,N-1

(8)

(9)

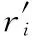
1.2.2 求解輸電線模型方程

根據式(2)、式(4)、式(5)確定(pi,qi)后，曲線簇可以被唯一確定。本節將說明姿態—曲線算法如何計算復數(pi,qi)使之滿足4個約束，式(2)～式(5)結合約束式(6)～式(9)得到式(10)～式(14)

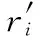
(10)

(11)

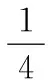
(12)

(13)

(14)

|qi-1-2qi+qi+1|2)

(15)

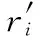
切線約束：式(10)中計算的切線應當滿足實際MARG計算得到的切線di=(dxi,dyi,dzi),i=0,…,N，得到式(12)。

弧長約束：式(13)計算了每一段曲線的長度，應該等于實測值li。將式(4)、式(5)代入式(13)，可將每段曲線的長度li用復數對(pi,qi)表示。

首尾位置約束：設該輸電線首尾兩端相對距離Δd=(Δx,Δy,Δz)。將式(2)代入約束方程(7)得到式(14),式(14)也可以用復數對(pi,qi)表示。

目前，四個約束(式(6)～式(9))均能由復數對(pi,qi)表示，式(12)～式(14)共包含了4N+6個標量方程，復數對(pi,qi)中共含4N+8個變量，故姿態—曲線還原算法使用最小化函數式(15)的方法確定(pi,qi)。式(15)可理解為五次曲線到三次曲線的“距離”，描述了輸電線的平滑性，值越小輸電線越平滑。使用現有的最優化方法求解最小化函數式(15)[8]。最優化計算中，與真值接近的初始值(pi,qi)init可降低姿態—曲線還原算法的運行時間。在姿態—曲線還原算法中，每一個時刻的初值(pi,qi)init設置為上個時刻得到的最優值(pi,qi)optimal。關于初始時刻的最優化初值，可以使用表示輸電線靜止時的(pi,qi)stabie作為初值。

2 仿真實驗

使用Matlab作為仿真環境，對比基于加速度的監測系統和基于姿態的監測系統在兩種輸電線舞動模式下的還原效果:1)最簡單的擺動模型;2)來自于對真實輸電線舞動的有限元模擬數據[9]，該模式下輸電線做無規則運動。文中對比實驗中，基于加速度的舞動還原系統的初始位置均為零時刻位置。

2.1 輸電線擺動模式舞動還原

該模式下，輸電線在無風靜止呈垂鏈線狀，開始舞動時輸電線上各點多作類單擺運動，運動平面垂直于輸電線方向，同時輸電線會沿其切線方向做扭轉運動。監測系統于輸電線綁定了5個MARG。

圖2對比了位于輸電線中點的MARG的位移圖像。在這種舞動模式下，兩種系統的還原結果均較準確。這種模式中由于該MARG運動中心并未發生變化，因此，基于加速度系統的劣勢并不明顯。圖2(a)中，基于加速度系統的結果在X軸上有近0.3m的運動，這是由于該系統計算姿態不夠準確所致。基于姿態的還原系統不僅能得到絕對的位移，并且在位移幅度和位移平面上也與真實值非常相近。

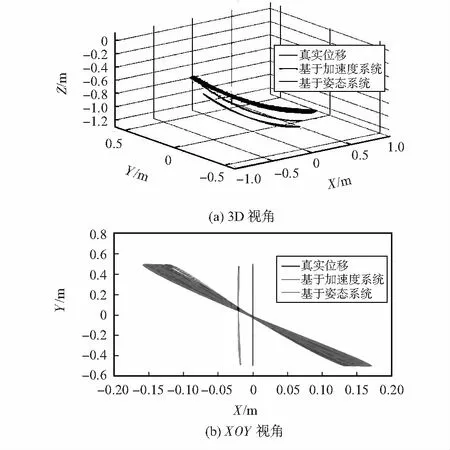
圖2 MARG位移還原(擺動模型)

圖3對比了某個時刻兩種監測系統對輸電線整體形狀還原效果。兩者均較為準確地獲得正確的輸電線形狀。

2.2 有限元模擬輸電線舞動數據還原

現實中，輸電線做不規則舞動，監測該輸電線使用6只傳感器。圖4對比了某個MARG的位移圖像，圖中基于姿態系統的還原結果與真實值非常相似，而基于加速度系統與真實值相差較遠。這是由于基于加速度的系統無法測量MARG的低頻運動，而基于姿態的系統因為可獲得絕對位置，故還原效果更準確。

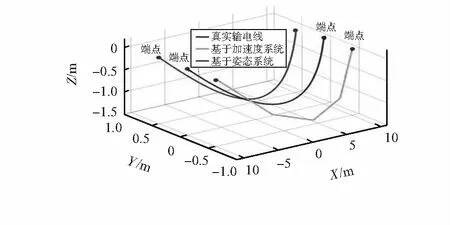
圖3 輸電線還原(簡單模型)

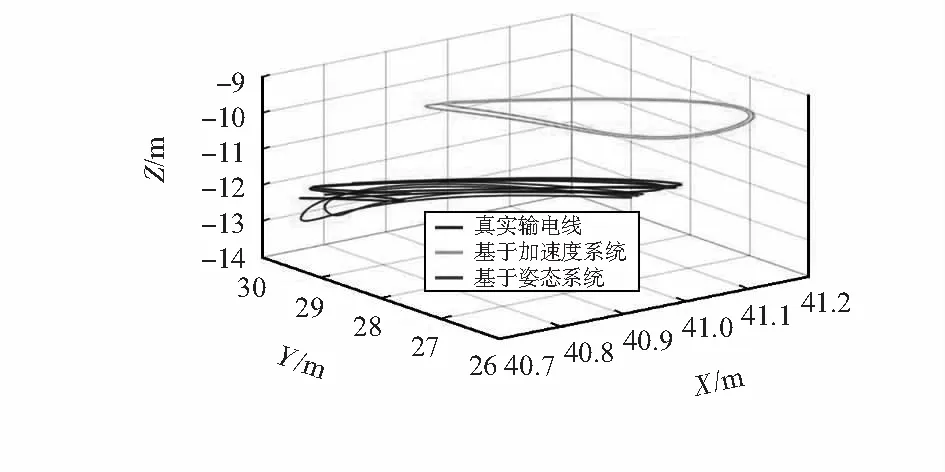
圖4 MARG位移還原(有限元設計模型)

圖5為某個時刻兩種監測系統還原整根輸電線的效果。基于加速度的系統只能獲得相對位置，當MARG運動中心變化后該系統無法獲得準確的采樣點位置，導致最終還原結果錯誤。基于姿態的監測系統則仍然能準確地獲得輸電線的實時舞動形狀。

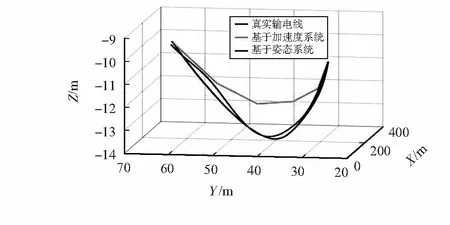
圖5 輸電線還原(有限元設計模型)

3 結束語

針對現有的輸電線監測系統所存在的4個缺陷，提出了姿態—曲線還原算法，主要原理是通過MARG的姿態計算輸電線的舞動形狀，并代替了現有的基于加速度積分的算法。在硬件架構上，基于姿態的舞動監測系統與現有系統完全相同，因此，姿態—曲線還原算法可以直接應用到現有的舞動監測系統中，并得到更為準確的結果。使用本算法的優勢在于能夠獲得絕對位置、位移幅度更精確并且可以獲得整根輸電線的舞動形狀。

[1] 王少華,蔣興良,孫才新.輸電線路導線舞動的國內外研究現狀[J] 高電壓技術,2005,31(10):11-14.

[2] Lü Zhongbin,Li Qing,Ni Yiqing,et al.An efficient method for galloping profile monitoring of power transmission lines by use of an inertial unit:Theoretical and experimental investigation[C]∥Advances in Structural Engineering and Mechanics,Korea:Incheon,2015:22-29.

[3] Crassidis J L,Markley F L.Unscented filtering for spacecraft attitude estimation[J].Journal of Guidance,Control,and Dynamics,2003,26(4):536-542.

[4] Xie K,Zhang C,Li Q,et al.Tracking galloping profile of transmission lines using wireless inertial measurement units[J].Journal of Computer and Communications,2015,3(5):220.

[5] Trawny Nikolas.Indirect Kalman filter for 3D attitude estima-tion[J].Twin Cities,Minnesota:University of Minnesota,2005.

[6] Farouki Rida T.Pythagorean hodograph curves[M].Berlin Heidelberg:Springer,2008.

[7] Huard Mathieu.C2 interpolation of spatial data subject to arc-length constraints using pythagorean hodograph quintic splines[J].Graphical Models,2014,76(1):30-42.

[8] 陳寶林.最優化理論與算法[M].北京：清華大學出版社,2005.

[9] Hu J C,Song Z,Ma J G.Model for comprehensive simulation of overhead high voltage power transmission line galloping and protection[C]∥IEEE Conference on Electrical Insulation and Dielectric Phenomena,IEEE,2006:190-193.

ResearchonpowertransmissionlinegallopingmonitoringalgorithmbasedonmultipleMARGsensorattitude

ZHU Qin-xiang, GUO Wei, ZHANG Gang

(StateKeyLaboratoryofAdvancedOpticalCommunicationSystemsandNetworks,ShanghaiJiaoTongUniversity,Shanghai201100,China)

Monitoring the motion of power transmission line(PTL)through magnetic angular rate and gravity (MARG) sensor array,including accelerometer, magnetometer and gyroscope,is one of the most mature technology in PTL monitoring system.However,it suffers lot of principle problems,such as initial point of position integration is unknown and the low frequency movement information of PTL is easy to be lost.Propose a new attitude-based algorithm to estimate real-time movement of PTL during galloping: it fuses the attitudes of multiple MARG sensor deployed on the PTL to calculate the displacement of MARG sensor as well as the movement of PTL.With this algorithm,integration cumulative error in displacements can be avoided,solve length constraints of PTL and recover PTL galloping movement image accurately through just a small number of MARG sensor.Simulations prove that this algorithm can reduce amplitude error of PTL galloping,and restoring error can′t increase with time.

magnetic angular rate and gravity(MARG)sensor; attitude-curve recovery algorithm; power transmission line(PTL)galloping; attitude

10.13873/J.1000—9787(2017)11—0021—04

TP 212

A

1000—9787(2017)11—0021—04

2016—11—09

朱勤翔(1989-)，男，碩士，主要從事基于MARG的導航定位方面及輸電線舞動監測方面的研究工作。