基于溫度效應的橋梁動態稱重識別研究

,， ，

(1.浙江工業大學 建筑工程學院，浙江 杭州 310014；2.浙江省交通建設工程監督管理局，浙江 杭州 310000)

基于溫度效應的橋梁動態稱重識別研究

張豪1,陳尚新2，余敏1，龔豪1

(1.浙江工業大學 建筑工程學院，浙江 杭州 310014；2.浙江省交通建設工程監督管理局，浙江 杭州 310000)

以橋梁不同截面動應變響應為對象，分析識別不同截面的動應變數據，及荷載通過不同截面的時間差，進行車速識別.通過荷載在不同截面的應變影響線以及識別車速，獲得動應變影響面積，利用影響面積與動荷載的相關關系，進行移動荷載識別研究，得到橋梁動態稱重系數.據結構應變與溫度的相關特性，通過對溫度與應變的回歸分析，確定其具體的經驗回歸方程，將溫度所致的應變變化趨勢從總的應變測量值中分離.對分離溫度效應前后的稱重系數進行對比，得到溫度效應對橋梁動態稱重的影響.

動應變；橋梁動態稱重系數；回歸分析；溫度效應

我國橋梁眾多，近年來由于超載所導致的橋梁健康事故頻發，移動荷載作為影響橋梁使用壽命的主要因素之一，對于橋梁健康狀態的評估以及運營維護管理等方面都具有重要意義.目前，橋梁移動荷載的識別方法主要有兩種：一種是利用車—橋耦合的振動模型來分析車輛和橋梁接觸處的相互作用力來識別移動荷載[1]，Deng等[2]結合車—橋耦合振動模型進行數值計算，并以橋梁動力響應為研究對象通過影響面疊加識別車輛動態軸重，并研究了橋梁慣性力及其他因素影響，王寧波等[3-4]將車一橋耦合振動進行結合、模擬.當車駛過橋面時，橋的各個截面上所布置的測點會產生相應的動應變響應，對該響應進行研究，選取應變曲線峰值點，通過一定算法對車的速度、軸距和軸數等進行計算.通常應變曲線影響面積與車輛重量會有一定的比例關系，我們可以利用這樣的關系對車輛實施動態稱重.同時通過影響線擬合動力響應的思路來對軸重進行計算.這種方法需要的系統參數多，所計算出的結果就是車輛與橋面的動態接觸力，路面平整與否、行車速度快慢都有較大影響.另一種方法是利用移動荷載的動力響應對橋梁上車輛的車速、軸距、軸數以及軸重等進行直接地識別[5]，Chatterjee等[6]對車子經過橋時橋梁的動應變響應進行探討，使用離散小波變換的方法對軸距、車軸數量等參數進行計算，通過進行許多試驗以及使用數值仿真分析對其驗證.移動荷載識別方法需要的系統參數少，可識別的信息量大，可操作性高.實踐證明：實測的動力響應信號易受環境因素的影響(如頻率、動應變)，橋梁動態監測以動應變及延伸的車速監測為基礎，已有研究表明了溫度對于采集到的動應變數據影響是非常大的，溫度驟變或季節性變化對應變都有很大的影響[7]；而余敏[8]也證明了溫度變化往往影響動應變峰值點，從而通過影響車速監測，最終影響車重監測，故基于動力響應的方法必須考慮環境因素的影響.

由于采用數值模擬往往在實際應用中受到環境因素變化的約束，而通過實測進行橋梁動態稱重往往以大型橋梁為研究對象，以中小型橋梁為研究對象的也很少考慮環境因素[9-13]，但根據統計，浙江省

內截至2013年，中小型橋梁所占比例為92%，因此進行考慮環境因素中小型橋梁的動態稱重研究具有十分重要的工程意義.針對小型橋梁，并以車輛通過橋梁不同截面的實測應變數據為研究對象，以環境因素中的溫度作為影響因素，分析了車輛動態稱重系數k的識別方法，并對剔除溫度影響前后的車輛動態稱重系數k進行分析，從中得出溫度效應對于橋梁動態稱重的影響.

1 橋梁動應變采集與分析

文中以鹽家塘橋右幅采集的數據為研究對象，該橋梁位于01省道復線、嘉興東西大道，橋型為XX裝配式預應力混凝土簡支T梁橋，全橋長約106 m(僅采集到前兩跨數據)，前2跨應變傳感器布置如圖1所示.

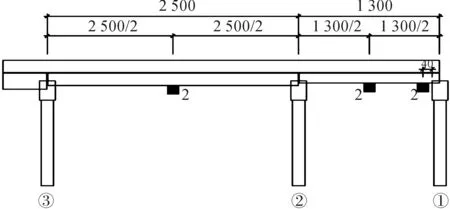
圖1 鹽家塘橋右幅傳感器布置圖Fig.1 Sensor layout on the right of Yanjiatang

從圖1中可以看出：各傳感器布置位置的信息(圖中單位為cm)，鹽嘉塘橋為單向兩車道，故每一車道布置一個應變傳感器；橋梁上布設一個溫度傳感器.規定的行車方向按橋墩號為1～3.

按照行車的方向，將3個截面的傳感器分為A，B，C三組.分別將車重為10 t和20 t的三軸試驗車在橋梁上反復行駛，試驗車具體信息如表1所示.

表1 試驗車輛系數Table1 The coefficient of test cars

試驗車輛經過橋梁時，傳感器采集得到的動應變數據如圖2所示.

從圖2可以看出：從車輛上橋開始，各個傳感器的動應變開始呈上升趨勢；車輛正好壓在傳感器截面，應變達到峰值；車輛下橋后，由于活荷載消失，動應變數據又趨于平穩，且不同截面的傳感器波形與傳感器的安裝位置相符.而20.3 t車過橋時的動應變峰值明顯大于10.6 t車.說明本次試驗采集到的數據跟實際情況相符，可作為后期處理數據依據.

2 車輛動態稱重系數識別

將車輛上橋至完全出橋時間段內應變曲線對橫軸(代表空間坐標)積分，就可以得到應變曲線的影響面積[14]，即

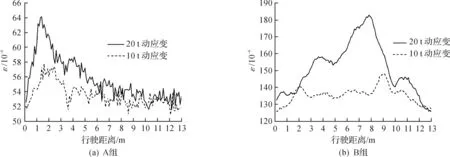
圖2 兩組傳感器動應變原始數據Fig.2 The total dynamic strain of series A and B

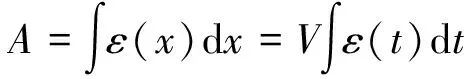
(1)

式中：ε(t)為動應變；A為影響面積；V為行駛車輛速度.

通過式(1)計算影響面積需對車輛的上下橋時間進行識別，可將圖2的應變曲線轉換到時域，如圖3所示.

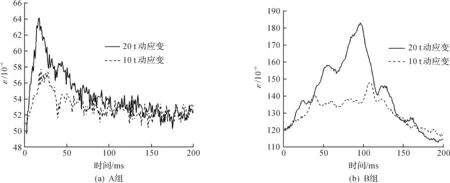
圖3 兩組傳感器動應變原始數據Fig.3 The total dynamic strain of series A and B

由于不同截面測點間的距離已知，根據不同測點間識別的峰值時間tA，tB，tC，就可以得到車輛在2個測點之間的車速，即

VAB=6.1/(tB-tA)；VBC=19/(tC-tB)

(2)

由式(2)可推導出車輛的上下橋時間，上橋時間ts=tA-0.4/VAB，下橋時間tx=tC+12.5/VBC.根據上下橋時間可求得的平均車速，式(1)中的V=38/tx-ts.如果路面的粗糙度、行車速度和車重量不一樣，則應變曲線都會有所改變，使得應變影響面積有所變化，文獻[4]中證明盡管行車速度和路面粗糙度的確會使得應變曲線有較大地改變，可是影響面積的計算改變較小，而且車輛的總重量會對其造成最大的影響.同時，文獻[4]中通過車橋耦合的模型結構對不同截面的應變影響面積與車重之間的關系進行了分析，結果表明了對于任意截面測點都存在

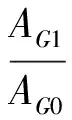
(3)

式中：G1，G0分別為兩不同車輛的總重；AG1，AG0分別為兩不同車輛對應的影響面積.定義稱重系數k，令

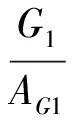
(4)

由式(4)可知：對于同一截面而言，稱重系數k應該為一個常數，它與橋梁本身的系統參數相關，橋梁結構若處于良好的營運狀態和健康狀況，橋梁的系統參數不會特別明顯，但是當出現損傷時，則可能由于橋梁的剛度變化，導致應變發生變化，從而引起稱重系數k發生明顯變化.也就是說，對于理想的模型，稱重系數k為一個可以反映橋梁健康狀況的系數，然而這種理論在實際橋梁應用中是否適應，在接下來的內容中將予以分析.

令k為稱重系數，其表達式為

k=應變影響面積/試驗車車重

剔除溫度效應前的稱重系數k的計算結果如表2所示.

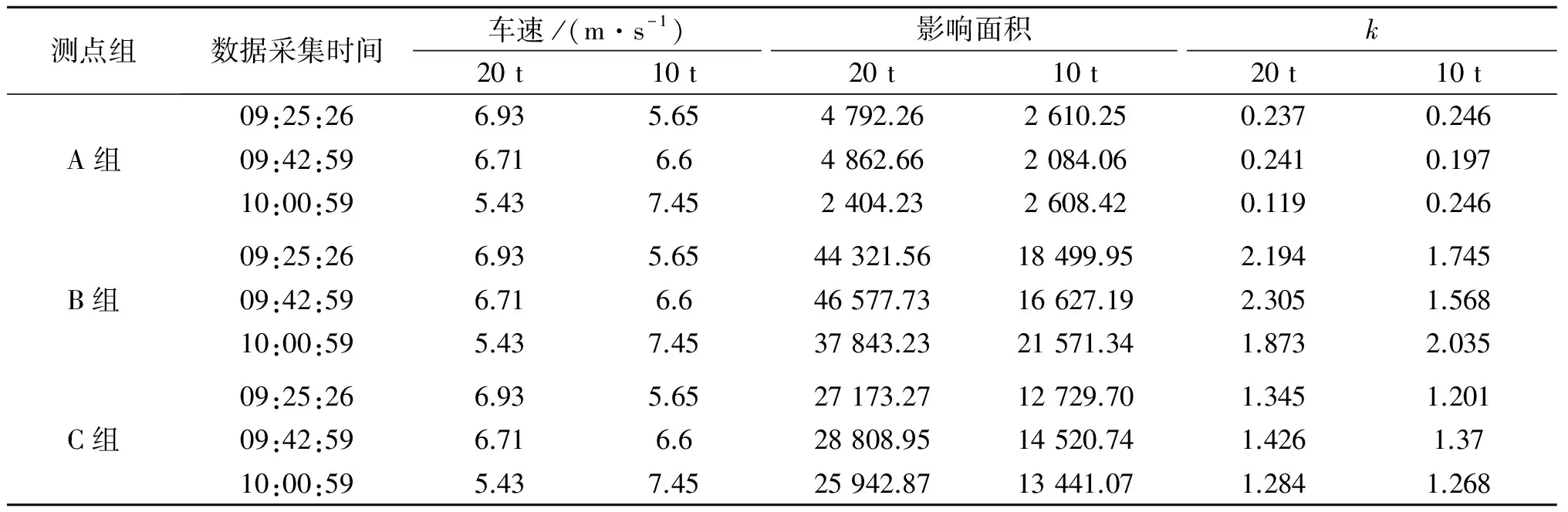
表2 剔除溫度效應前的稱重系數k值表Table 2 The total coefficient of bridge weigh-in-motion

3 動應變溫度效應的分離

3.1 動應變溫度效應分離方法

由橋梁結構分析[15]可知：在某一時刻，混凝土橋梁結構在某一點的總應變值可表示為

ε=εT+εL+εR

(5)

式中：εT為溫度應變，其中有溫度引起的結構應變和由溫度造成的測量傳感器自身的應變；εL為荷載(包括活荷載和恒載)產生的應變；εR為混凝土在收縮及產生徐變時所造成的應變.

橋梁健康狀態下，恒荷載造成的混凝土結構應變變化能夠近似地看作是恒定不變的，但由混凝土收縮及徐變造成的應變變化較大，呈指數衰減[16]，第1年中的變化占大部分(完成75%)，在之后的20年內，剩下的25%的會繼續完成，本實驗針對的橋梁可忽略由收縮和徐變產生的應變的影響.而由活荷載產生的應變則呈隨機變化，在彈性范圍內，若活荷載消失，橋梁結構將迅速恢復到初始狀態.溫度應變則具有周期性，隨溫度的變化而變化.雖然溫度對混凝土變形的影響機理非常復雜，但對于某一測點，應變的實測值當中由溫度變化產生的溫度應變，與溫度變化基本呈線性關系[17].因此盡管不能精確地計算出溫度產生的各種影響，但在實際工程實踐中，可以利用以上的關系，來對實測的應變進行分析，剔除溫度應變的影響.

由文獻[17]可知：混凝土橋梁應變和溫度的關系近似為一次線性關系，故可假設S=aT+b，式中：S為相應的應變；T為溫度；a，b分別為待定系數.利用最小二乘法對實測的應變和溫度數據進行

擬合，對a和b的值進行估計，即對于任意給定的樣本值(Si,Ti)(i=1,2,3,…,n)，令

(6)

的取值最小，就可得到a和b的估計值.故可對式(6)進行求導，設倒數為零，即

(7)

(8)

將式(7,8)聯立可得

(9)

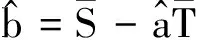
(10)

根據給定的樣本數據，利用式(9，10)分別求得a和b的估計值，從而確定應變和溫度的經驗回歸方程，并可由此剔除溫度應變.具體剔除過程可參考文獻[8]，剔除溫度效應后的動應變如圖4所示.

對比圖4，2可以發現：剔除溫度效應后的各傳感器應變波形基本保持了原始的形態.以上的回歸分析采用的是總應變，剔除溫度效應后，在沒有活荷載的前提下，橋梁應變近似于0，這與理論情況相符，同時也進一步證明了利用結構總應變作為數據樣本來剔除溫度效應的可行性.利用剔除溫度效應后的動應變數據，計算稱重系數k，得到的結果如表3所示.

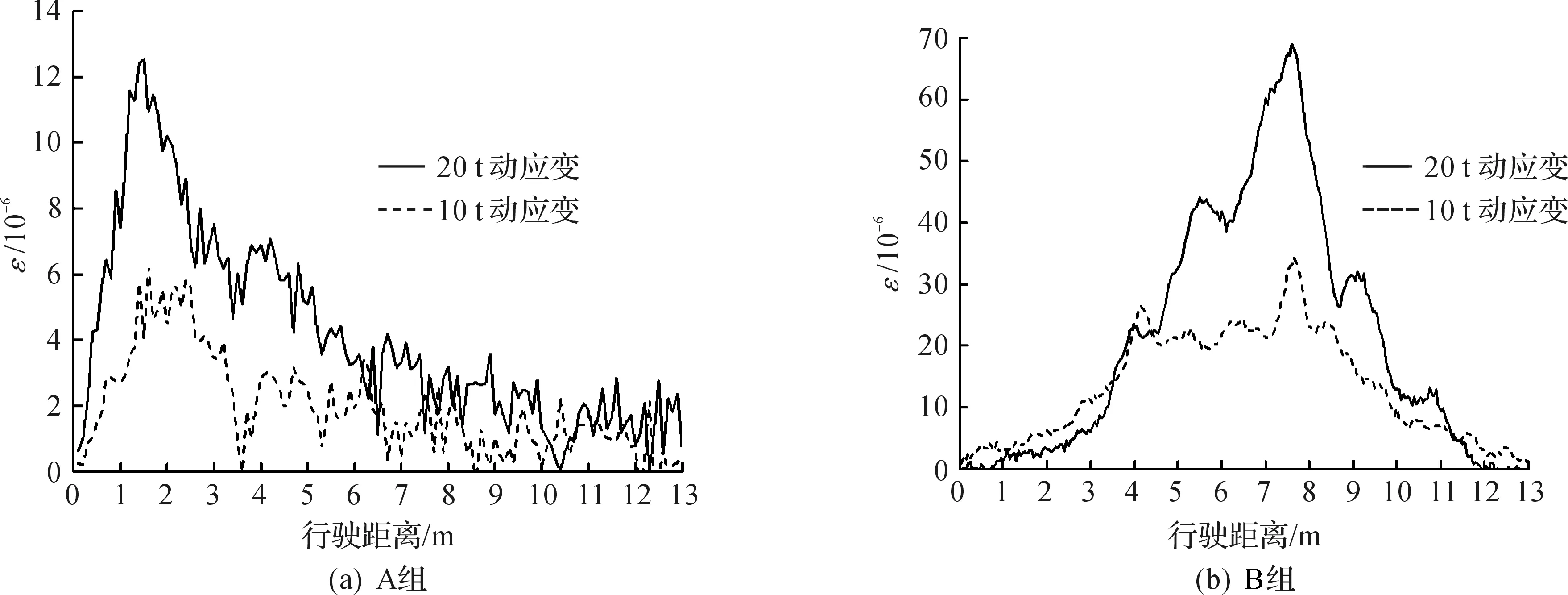
圖4 兩組傳感器剔除溫度效應后動應變數據Fig.4 The separated strain of series A and B

測點組數據采集時間車速/(m·s-1)20t10t影響面積20t10tk20t10tA組09：25：266．936．685609．952853．050．2780．26909：42：596．716．65558．682818．570．2750．26610：00：595．437．454576．292964．320．2270．28B組09：25：266．936．6853027．1628047．532．6252．64609：42：596．716．654407．1926612．852．6932．51110：00：595．437．4555306．8128876．802．7372．724C組09：25：266．936．6826190．8413716．231．2961．29409：42：596．716．627015．4413668．821．3371．28910：00：595．437．4525683．8913582．991．2711．281

3.2 剔除溫度效應前后稱重系數分析

剔除溫度應變前后的稱重系數對比如表4所示.

根據表4可知：無論剔除溫度效應前后，稱重系數k值的方差都非常小，考慮到實際交通中的影響因素，可判斷式(4)成立，即k值為常數.

表4 剔除溫度效應前后稱重系數k對比Table 4 Compared the coefficient of bridge weigh-in-motion on total strain with separated strain

3組數據在溫度效應剔除前稱重系數k的方差較大，表明k值的波動相對較大，其原因在于，剔除溫度效應前，根據式(1)計算影響面積需根據系統識別的車速來反推車輛的上下橋時間，而這種方法容易因為車速識別不準確而造成較大誤差.而剔除溫度效應后，車輛的上下橋時間較為直觀，所得的影響面積較為準確，故得到的稱重系數k之間的差距較小.除B組誤差較大，可以看出A和C兩組數據在剔除溫度效應前后差距很小，這也證明了在橋梁正常狀態下，同截面的稱重系數k只跟橋梁本身特性相關，而與橋梁上車輛的車速和車重無關.剔除溫度效應可以得到更加準確的稱重系數k，從而使橋梁動態稱重更加精確.

將表4中每一測組k值分別剔除最大值和最小值，對其他的k值求均值，得到的結果作為該截面的識別k值，結果如表5所示.

表5剔除溫度效應前后稱重系數

Table5Thecoefficientofbridgeweigh-in-motionontotalstrainwithseparatedstrain

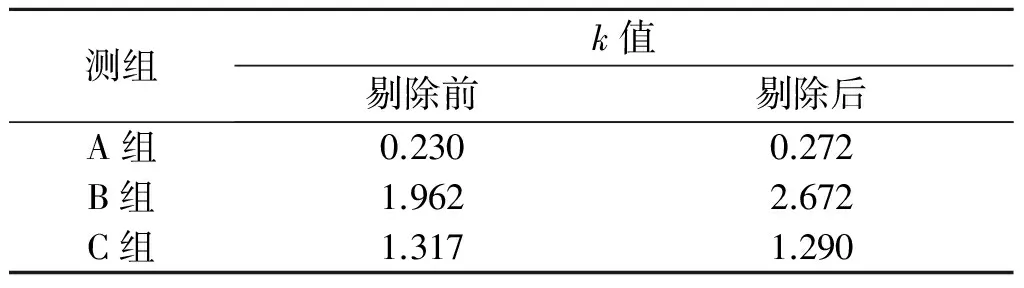
測組k值剔除前剔除后A組0．2300．272B組1．9622．672C組1．3171．290

4 現場車重識別結果

根據表5的k值，以及式(6)就可以通過識別車輛過橋時的影響面積來識別車重.假設3個截面的識別結果分別為GA，GB，GC，對3者取平均值，視為最終的識別車重，即

G=(GA+GB+GC)/3

(11)

將兩試驗車輛分別以10，20，40 km/h 3種車速6種工況通過橋梁，基于以上方法對車重進行識別，結果如表6所示.

從表6可以看出：通過稱重系數識別車重的方法是可行的；剔除溫度影響前的識別車重最大誤差為13.4%，剔除后最大誤差為6.0%；較大車重的識別誤差往往小于較小車重的識別誤差；剔除溫度影響前的誤差隨著車速變大而呈現變大趨勢，而剔除后的誤差則沒有明顯的遞增或遞減的趨勢.原因在于剔除溫度影響前，根據式(2)及其推論計算的上下橋時間容易由于識別車速的誤差而產生誤差，從而導致了應變影響面積的誤差，而該系統對于高速運行車輛的識別車速能力較為有限.剔除溫度影響后，車輛在上下橋時間內的波形較為直觀，這是識別車重誤差較小的原因.根據式(1)，剔除溫度影響后的應變影響面積仍然受識別車速的影響，故車速的準確識別是提高此種動態稱重方法的關鍵.

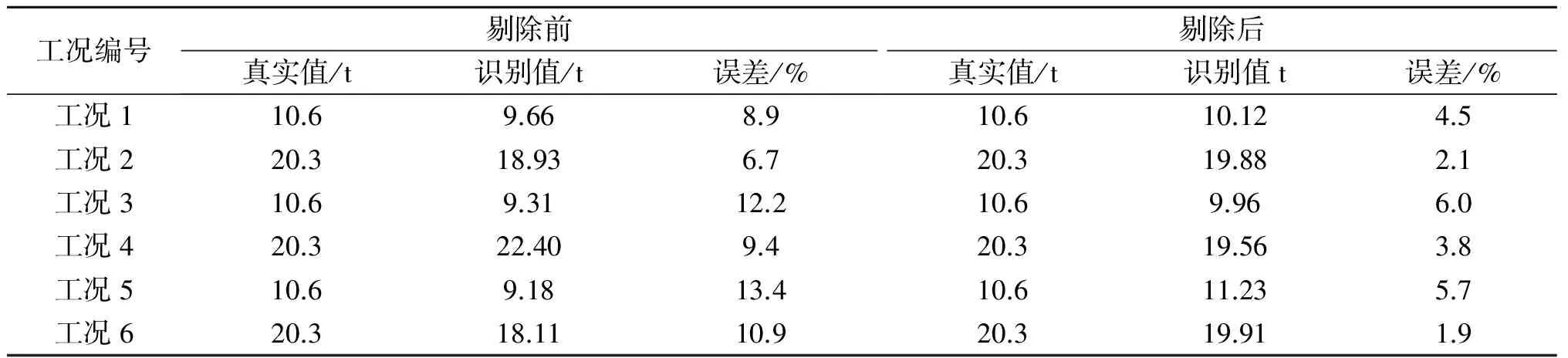
表6 剔除溫度效應前后的識別車重Table 6 The weight of bridge weigh-in-motion on total strain with separated strain

5 結 論

以中小型橋梁結構動應變響應為研究對象，闡述了動態稱重系數k的識別方法，并通過分析分離溫度效應前后的稱重系數，結果表明：通過計算動應變影響面積識別稱重系數k的方法實現橋梁動態稱重，需要的系統參數少，可行性強，具有較大的實際意義；車速的準確識別是提高此種橋梁動態稱重方法的關鍵；用總應變測量值減去擬合得到的溫度效應值，即可將溫度效應分離，相減得到的應變殘差可認為是荷載在這一期間所引起的應變值.沒有車輛荷載經過時，其值近似為0；通過溫度效應分離可以更直觀地得到車輛上下橋時間內的完整波形，提高橋梁動態稱重的精確度.

[1] 李忠獻,陳鋒.簡支梁橋與多跨連續梁橋上移動荷載的識別與參數分析[J].工程力學,2006,23(12):91-99.

[2] DENG L,CAI C S. Identification of dynamic vehicular axle loads：theory and simulations[J].Journal of vibration and control,2010,16(14):2167-2194.

[3] 王寧波,任偉新,李苗.基于影響線的橋梁移動荷載識別[J].振動與沖擊,2013,32(3):130-133.

[4] 王寧波,任偉新,萬華平.基于動應變的橋梁動態稱重及其優化算法[J].振動與沖擊,2013,32(4):117-120.

[5] SAKAYANAGI H, SASAKI E, THEERAPHONG C, et al. Analysis of axle position information from strain history data with long influence lines[J]. Journal of structural engineering,2008,54A:582-589.

[6] CHATTERJEE P, OBRIEN E, LI Y, et al. Wavelet domain analysis for identification of vehicle axles from bridge measurements[J]. Computers and structures,2006,84(28):1792-1801.

[7] 劉興法.混凝土結構的應力分析[M].北京:人民交通出版社,1991:16-18.

[8] 余敏.溫度效應對橋梁健康監測的影響[D].杭州：浙江工業大學,2016.

[9] 楊丹.基于分布式傳感的中小型橋梁荷載識別技術研究[D].南京：東南大學,2013.

[10] SHAHAWY MA,AROEKIASAMY M.Field instrumentation to study the time-dependent behavior in sunshine skyway bridge[J].Journal of bridge engineering,1996,1(2):76-86.

[11] 郭健,裘力奇,張新軍,等.基于小波包分析的橋梁支座損傷識別試驗研究[J].浙江工業大學學報,2016,44(6):695-698.

[12] 趙志方,王剛,周厚貴,等.混凝土拉伸軟化曲線確定方法的對比研究[J].浙江工業大學學報,2015,43(4):455-459.

[13] 楊楊,蔡陽,江晨暉,等.埋入式低彈模混凝土應變傳感器的研究[J].浙江工業大學學報,2015,43(4):450-454.

[14] KOBAYASHI Y, MIKI C, TANABE A. Long term monitoring of traffic loads by automatic real-time weigh-in.motion[J]. Journal of structural mechanics and earthquake engineering,2004,69:99-111.

[15] 華孝良.橋梁結構非線性分析[M].北京:人民交通出版社,1997.

[16] 蘇清洪.加筋混凝土收縮徐變的實驗研究[J].橋梁建設,1994(4):11-18.

[17] 陳常松,顏東煌,陳政清,等.混凝土振弦式應變計測試技術研究[J].中國公路學報,2004,17(1):29-33.

Researchonthedynamicweightindentificationofbridgesbasedontemperatureeffect

ZHANG Hao1, CHEN Shangxin2, YU Min1, GONG Hao1

(1.College of Civil Engineering and Architecture, Zhejiang University of Technology, Hangzhou 310014, China;2.Traffic Construction Engineering Administration of Zhejiang Province, Hangzhou 310000, China)

The dynamic strain responses at different cross-sections of a simply supported girder bridge are studied. The vehicle speed is identified by analyzing the dynamic strain data and loading time difference at different cross-sections. The influence line of the dynamic strain is obtained by loading the strain influence line at different cross-sections and by identifying the vehicle speed. Moving loads are identified with the relationship between the influence line and the dynamic load and the coefficient of bridge weigh-in-motion is obtained. According to the characteristics between the temperature and strain of bridge structures, an empirical equation is formulated by regressive analysis. The temperature effect of strain can be separated from the total strain. By comparing the coefficient of bridge weigh-in-motion with and without the temperature effect, the influence of temperature on the bridge weigh-in-motion can be determined.

dynamic strain; coefficient of bridge weigh-in-motion; regressive analysis; temperature effect

2017-03-06

浙江省交通運輸廳科技項目(ZJOB-JTT-201429)

張 豪(1961—)，男，江蘇南京人，教授，博士，研究方向為結構健康監測，E-mail：zhanghao@zjut.edu.cn.

TU375

A

1006-4303(2017)06-0682-06

(責任編輯：劉 巖)