外吹式襟翼動力增升效果評估方法

張聲偉， 王偉

中航工業第一飛機研究院， 西安 710089

外吹式襟翼動力增升效果評估方法

張聲偉*， 王偉

中航工業第一飛機研究院， 西安 710089

外吹式動力增升襟翼可以有效地縮短運輸類飛機的起降距離，其增升效果評估方法是運輸機動力增升設計的關鍵技術之一。本文采用基準氣動力耦合速度修正方法，發展了一套適用于外吹式襟翼動力增升效果快速評估的計算方法；該方法充分考慮了動力增升飛機性能計算對氣動力數據的需求，解決了傳統推力系數法的小速度大推力系數求解限制問題、無法準確求解離地速度以及多速度點氣動力求解引起的計算效率問題。以某運輸機為例，分析了其氣動力及起飛性能，對其外吹式襟翼動力增升效果進行了評估，驗證了方法的正確性。研究表明：通過優化動力增升襟翼偏轉角，起飛滑跑距離最大減小量可達到25%；過大的襟翼偏轉角將顯著地增加飛機阻力，不利于縮短起飛滑跑距離。研究工作對運輸機的外吹式動力增升襟翼設計，具有一定的工程指導價值。

外吹式襟翼； 動力增升； 氣動力計算； 性能收益評估； 襟翼構型優化

短距起降是現代軍用飛機設計追求的重要性能指標之一。對于大中型運輸機而言，短距起降與高速巡航是飛機氣動布局設計中一對難以兼容的性能指標。美軍C-17運輸機采用下蒙皮外吹式襟翼動力增升技術，有效協調了這一設計矛盾。C-17A運輸機翼載荷高達751.7 kg/m2，巡航速度為0.77馬赫數，是飛行速度最快的一款現役大型軍用運輸機。采用外吹式襟翼動力增升技術，高翼載并未使其起飛與著陸的場域性能惡化，反而相對于常規大型軍用運輸機的起降性能有了明顯的改善。由此可見，動力增升技術對于大中型軍用運輸機性能提升具有重要意義。

國內外關于動力增升技術的研究主要集中在模擬動力影響的風洞試驗[1-5]、考慮動力影響的CFD數值仿真計算[6-12]與飛機氣動布局對動力增升效果的影響[13-14]3個方面，關于動力增升效果評估技術的研究相對較少。動力增升飛機與常規飛機在起降場域性能計算與評估方法上存在顯著差異，主要體現在氣動力與起降場域性能計算方法兩個方面。動力增升飛機的布局形式，使其氣動力系數在起降階段受發動機噴流的影響很大，滑跑階段全機氣動特性曲線隨推力系數CT變化顯著。動力增升效果評估是短距起降運輸機的關鍵設計技術之一。

常規飛機起降性能計算僅需一套起降構型的氣動力數據，而動力增升飛機氣動力系數隨速度的動態變化特性使得用于起飛性能計算的關鍵參數：最大升力系數CLmax、抬前輪速度vR、離地速度vlof與安全速度v2均難以確定，性能積分運算無法進行。本文采用理論分析、風洞試驗、CFD數值仿真計算與算例飛機試驗數據驗證相結合的方法，對外吹式襟翼動力增升飛機低速構型的氣動力與性能計算方法進行了系統研究，建立了一套動力增升飛機性能評估的方法與程序。以某型運輸機為算例，計算并分析了由于動力增升所產生的起飛性能收益，驗證了方法的正確性；研究了不同襟翼偏角對起飛滑跑距離的影響,推重比與起飛重量對動力增升運輸機起飛場域性能的影響,為襟翼偏轉角優化方法提供參考。

1 氣動力計算

氣動力數值模擬仿真計算與基于推力系數概念的工程計算[15-16]是當前國際主流的動力增升飛機氣動力計算方法。推力系數法具有計算效率高、計算結果可信度好的優點，因此更適用于快速評估動力增升飛機的氣動特性，但其也存在一定的缺陷，如使用限制問題。在規定的推力系數范圍(0.48≤CT≤5.5)內該方法計算較準確，但在小速度大推力系數下無法使用，不能滿足飛機起降性能計算全速度區域積分運算的需要。

針對傳統推力系數法存在的使用限制問題，本文提出一套改進的氣動力計算方法，解決了傳統算法在小速度下氣動力發散，多速度點氣動力求解帶來的計算效率嚴重下降的問題。基本思想是：利用推力系數法計算某一速度(該速度位于可用范圍內)的氣動力，以該套氣動力作為基準氣動數據，利用不同速度點氣動力之間的函數關系，通過修正方法得到其他速度點的氣動力。

1.1 基準氣動力計算

動力增升效應產生的氣動力增量由噴流直接力與襟翼繞流兩部分組成。

1) 噴流直接力產生的氣動增量計算

(1)

式中：CLpush與CDpush分別為發動機噴流打在襟翼上產生的升力系數增量與阻力系數增量，是機身迎角α、噴流偏轉角θJ、噴流機身軸線夾角θe與推進效率因子ηJ的函數，θJ與發動機安裝位置、機翼安裝角θwin、襟翼偏轉角θflap、當地機翼相對弦長有關，推進效率因子ηJ是噴流最大理論偏角與噴流中機翼浸濕面積的函數。飛機構型確定后，噴流直接力產生的氣動力只與發動機可用推力有關。

2) 襟翼繞流產生的氣動增量計算

機翼下表面的發動機高速噴流經襟翼縫道，加速繞流到襟翼上表面，進一步加大了襟翼上下表面的壓力差，由此產生的氣動增量計算比較復雜。以升力系數計算為例，該部分升力系數增量由兩部分組成。其一是襟翼偏轉產生的升力系數CLbθ，另一部分來自于迎角變化產生的升力系數CLbα。該部分氣動增量計算涉及到多個參數，為適應本文計算方法，將計算公式分解成與推力系數相關與無關的兩類函數：

(2)

式(2)表明：襟翼偏轉產生的升力系數對推力系數比較敏感。與推力系數無關的函數fbθ與fbα只與飛機構型參數有關，如：機翼展弦比AR、噴流軸線處襟翼放出機翼的相對弦長C′、噴流對機翼展向影響因子φ、機翼后緣上表面的下傾角θf。迎角變化產生的升力系數主要由飛機構型決定，在小迎角狀態下，如起飛的滑跑階段，其產生的氣動力較小。

氣動力影響產生的阻力系數、俯仰力矩系數變化與升力系數變化機理相同，計算方法相似，具體計算公式可參見文獻[17]。

1.2 修正函數

推力系數法使用受限的原因是采用了推力系數的概念。當速度趨于零時，其對應的推力系數趨于無窮大。本文引入修正函數以描述不同速度氣動力之間的函數關系。以升力增量計算為例, 根據1.1節關于升力系數增量計算的分析，可將升力系數增量分解成與推力系數相關與無關的兩部分,即分解成與速度相關與無關的兩部分：

ΔCL=CLaer+CLpush=CT(KLbθ+KLpush)+CLbα

(3)

式中：CLaer為襟翼繞流產生的升力系數。與速度相關的參數為：襟翼繞流產生的升力系數計算因子KLbθ與噴流直接力產生的升力系數計算因子KLpush。將升力系數增量計算公式轉化為升力增量ΔL計算，即

ΔL=T(KLbθ+KLpush)+qSCLbα

(4)

式中：T為推力；q為速壓；S為機翼參考面積。

由式(4)可知，當飛機的構型與迎角確定后，參數KLbθ、KLpush與CLbα為定值。將升力增量計算公式對速度求導可得

(5)

式中：v為速度；ρ為空氣密度。

當速度由vi增加到vi+1時，全機的升力增量可表示為

(6)

式(6)表明：得到某一速度點的氣動力數據，則可計算出其相鄰速度點的氣動力，依次類推即可得到所有速度點對應的氣動力增量。如此即可解決傳統方法存在的計算速度盲區的問題。

氣動力的速度修正函數來自于發動機推力對速度的微分函數。典型的大涵道比渦扇發動機的推力速度曲線一般均可擬合成速度的多次函數。通過對擬合函數的求導，用微分解析的方法計算其他速度點的氣動力。若發動機的推力速度曲線不規則，可通過輸入發動機的推力速度數據，采用插值方法得到推力速度曲線在某速度點的曲率，以計算相鄰速度點的氣動力。

2 起飛性能計算

動力增升技術在提高飛機最大升力系數的同時，氣動阻力也大大增加，升阻比下降。這種高升高阻的氣動特性有利于實現短距著陸，但對于起飛則是既有利也有弊。如阻力過大，可能造成起飛距離增大，單發失效與復飛情況下的爬升能力無法滿足設計規范或適航條例的要求，影響飛行安全。需要對起飛構型進行優化，以協調升力與阻力之間的矛盾，因此本文重點研究起飛構型的性能計算。

2.1 起飛受力分析與性能積分計算

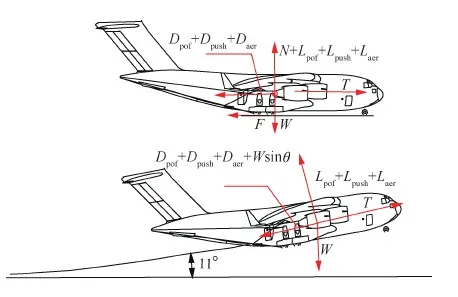
圖1 動力增升飛機起飛過程受力示意圖Fig.1 Sketch of forces on powered high-lift aircraft in takeoff

吹氣襟翼式動力增升飛機起飛過程受力情況見圖1。圖中Lpof與Dpof分別為算例飛機無動力影響下的升力與阻力，Lpush與Dpush分別為發動機噴流直接力產生的升力與阻力增量，Laer與Daer分別為噴流襟翼繞流產生的升力與阻力增量，F為飛機滑跑產生的摩擦力,N為地面支撐力,θ為飛機爬升航跡角，W為飛機重量。

相對于常規飛機，動力增升飛機縱向與法向分別多出了兩項力：Dpush、Daer與Lpush、Laer，由發動機噴流直接力與襟翼繞流作用產生。根據受力分析與氣動力增量計算公式，得出地面滑跑、抬前輪至離地與離地爬升到安全高度3個起飛階段的積分表達式為

(7)

式中：μ為滾動摩擦系數；發動機噴流變化修正系數E為發動機推力T與來流速度v的函數。

2.2 性能計算存在的問題與解決方法

國外關于動力增升飛機性能計算方法公開發表的研究論文不多，主要內容見文獻[18-19]，這些方法在工程應用中存在以下問題需要解決：

1) 離地速度的計算

動力增升技術通過減小離地速度，以縮短起飛距離。準確的離地速度是準確計算起飛性能的保障。動力增升飛機最大升力系數隨速度變化顯著，因此離地速度無法按常規方法計算。

由于升力隨速度非線性增大，以較大的速度作為初始計算速度vcp，采用二分法或切線法，通過循環迭代逐步減小計算速度，數值求解可用的離地速度。計算表明：用無動力狀態的最大升力系數計算的離地速度作為初始計算速度，計算收斂的速度較快。數值求解的收斂條件為：以離地速度計算得到的升力等于飛機起飛離地時的重力，并且將計算速度與離地速度差值的相對量控制在1%以內。收斂條件的意義是：使解算得到的離地速度與計算速度所對應的氣動力數據保持一致，保證以離地速度計算的升力Llof等于飛機離地瞬間的重力Wlof，同時還要防止計算速度偏大，導致離地速度與起飛距離的計算值偏大。

根據設計規范中抬前輪速度、安全速度與離地速度的相對關系，可得到vR與v2的值。

2) 性能計算中氣動數據的使用

動力增升飛機性能計算的基本方法與常規飛機無異，只是在氣動數據的使用上存在顯著差異。性能計算與氣動計算聯系更緊密，也更復雜。由于存在多個推力系數對應的多套氣動數據，性能計算中氣動數據使用不便，計算效率很低。通過采用基準氣動力耦合速度修正的方法，使起降性能計算只需一套基準氣動力數據與一個修正函數，有效地提高了性能計算效率。將氣動計算分解成多個模塊，并將其嵌入在性能計算相應的位置，起飛性能計算流程見圖2，Wto為起飛質量。

圖2 動力增升飛機起飛性能計算流程 Fig.2 Compute process for takeoff performance of powered high-lift aircraft

根據圖2所示的離地速度計算流程可得到準確可用的離地速度，并以該速度點對應的氣動力數據作為基準數據。對發動機的推力速度曲線數據，采用解析或插值方法得到推力對速度的微分函數或曲線斜率插值，依次計算相鄰速度點的氣動力，直到完成性能計算所覆蓋的速度區域。最終通過性能計算程序完成飛機起飛性能的計算。圖2所示的計算流程由兩部分組成：氣動計算模塊提供了抬前輪速度、離地速度、安全速度與氣動力計算所需的基準數據；性能計算模塊使用本文性能計算積分公式與計算方法完成起飛場域性能的計算。

3 算例分析與驗證

算例飛機采用下蒙皮吹風式襟翼動力增升技術。機翼面積為353 m2,翼展為50.29 m，展弦比為7.2，機翼1/4弦線后掠角為25°，梢根比為0.22。起飛構型：前緣縫翼偏角為15°，襟翼偏角為25°。內側發動機展向安裝位置為32.2%的半展長，外側發動機展向安裝位置為58%的半展長。

飛機機翼下吊掛4臺大涵道比渦扇發動機，每臺推力185.5 kN。發動機推力軸線相對于當地機翼弦線的偏角為-5°。發動機噴口距機翼前緣1.6 m，與機翼前緣垂直距離為0.9 m。算例飛機構型數據來源于文獻[20]，發動機起飛狀態的推力速度曲線數據參考了推力為189.5 kN的 RB211-535E4-Bs大涵道比渦扇發動機。

3.1 氣動力與起飛性能計算

當無法得到飛機的真實氣動數據時，通過性能計算來間接驗證氣動力計算值的準確性是飛機設計常用的方法。起飛場域性能計算條件包括：標準大氣，無風，機場高度為0 m，起飛質量為265.35 t。算例飛機無動力狀態起飛構型最大升力系數計算值為2.15，離地速度為86 m/s。以此速度作為初始計算速度，經過6次循環迭代，得到可用的離地速度。收斂時的計算速度與所得離地速度相對差量為0.5%，相關數據見表1。

離地速度對應的主要參數：推力系數為0.523，推進效率因子為0.886，噴流偏轉角為15.3°，翼型后緣動量系數為0.71，該速度離地迎角為8.1°，氣動力產生的氣動增量數據見表2。

海平面標準大氣環境下，算例飛機發動機的推力速度擬合函數為

T=0.000 25v2-0.29v+185.5

(8)

推力的速度微分函數為

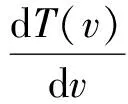
(9)

全機升力增量對速度的微分函數為

0.001 3v-0.776 8

(10)

由此可計算得到性能計算速度區域內的升力，阻力計算與升力計算方法相同。

表1 收斂速度對應的相關數據

表2離地速度下氣動力產生的氣動力增量

Table2Aerodynamicforceincrementofpoweredhigh-liftataircrafttakeoffspeed

Lpush/kNLaer/kNDpush/kNDaer/kN290．9251．6121．352．6

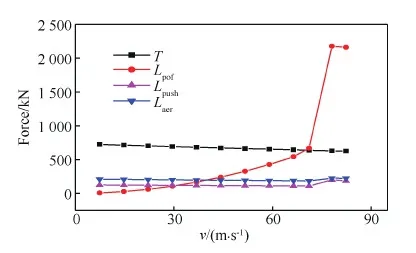
圖3 推力與法向力隨速度變化Fig.3 Thrust and vertical force vs velocity

圖4 推力與縱向力隨速度變化Fig.4 Thrust and longitudinal force vs velocity

離地速度計算收斂時，算例飛機起飛失速速度為67.5 m/s，抬前輪速度為70.85 m/s，安全高度速度為81 m/s。根據性能積分計算式(7)，得到算例飛機起飛階段的各項數據：滑跑距離為1 850.6 m,起飛距離為2 296.7 m，文獻[20]給出的起飛距離為2 360 m,計算誤差小于3%。圖3 與圖4為算例飛機起飛過程中各項力計算值隨速度的變化曲線。圖中曲線表明：氣動力影響產生的氣動力增量隨速度連續平緩變化，這與氣動力系數隨推力系數或速度的變化曲線完全不同。風洞試驗表明：隨著推力系數的增大，最大升力系數可達到9,甚至更高。大推力系數對應的小速壓乘以升力系數所得升力的變化量遠遠小于升力系數的變化量。動力增升飛機的氣動力系數曲線會給人造成一種錯覺，因此僅通過升力系數無法準確評價動力增升的效果。

用于研究動力增升運輸機氣動特性的模擬動力影響的風洞試驗、氣動力CFD數值模擬計算與工程估算表明：CFD計算數據在升力與力矩方面與風洞試驗數據在某些狀態點上吻合得較好，有些點則比較差，阻力計算值與試驗數據差別較大。工程估算方法計算的阻力更接近于試驗數據，升力與力矩計算數據較CFD計算數據精度差些，但計算數據比較穩定，在各狀態下計算誤差相差不大，計算效率明顯比CFD高。

3.2 算例飛機氣動特性分析

增升效果評估需要從氣動與性能2個方面進行評估。本文計算了算例飛機無動力影響與不同推力系數下的氣動力。表3為不同速度下飛機起飛過程中的主要氣動參數計算數據,CD α0為零迎角阻力系數，Kα0為零迎角升阻比。圖5與圖6顯示出不同推力系數對飛機氣動特性的影響。

當推力、機翼面積與大氣密度確定后，推力系數僅取決于來流速度。表3數據表明速度對最大升力系數影響非常大，25 m/s速度對應的最大升力系數是80 m/s速度的2.26倍，是無動力影響最大升力系數的2.8倍。25 m/s速度對應的零迎角升阻比比80 m/s速度下降了94.6%。圖7與圖8曲線表明最大升力系數與零迎角升阻比隨速度呈非線性變化，且變化梯度很大。

表3 主要氣動參數計算值Table 3 Main aerodynamic parameters calculation data

圖5 動力對升力曲線的影響Fig.5 Lift curves under powered high-lift effects

圖6 動力對極曲線的影響Fig.6 Polar curves under powered high-lift effects

表4為算例飛機0° 迎角，0.84推力系數下動力對氣動系數的影響量，表5將氣動增量進行了分解。表4中:ΔCL與ΔCD分別為升力與阻力系數的增量。計算表明：動力影響使飛機升力系數增加了76.9%，阻力系數增大了170.9%。阻力系數的增量明顯高于升力系數，升阻比減小了35.2%。性能計算表明：盡管動力影響會使升阻比下降，但如果將阻力增量控制在一定范圍內，使升力增量產生的性能收益大于升阻比下降帶來的性能損失,仍然可以達到縮短起飛距離的目的。螺旋槳飛機出色的起降場域性能也可說明這一問題。

表5數據表明:升力系數增量中的40.9%來自于噴流直接力，而直接力產生的阻力系數增量高達83.7%。由此可見，減小噴流直接力所占比重，有利于提高動力影響帶來的氣動效益。直接力產生的阻力系數是推進效率因子的函數，而襟翼偏轉角對推進效率因子的影響顯著。通過優化起飛構型的襟翼偏轉角，可有效提高動力增升效果。

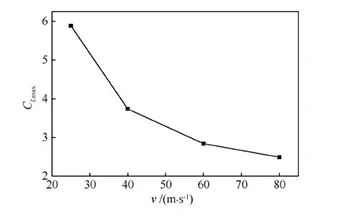
圖7 最大升力系數隨速度變化曲線Fig.7 Max lift coefficient curve vs velocity

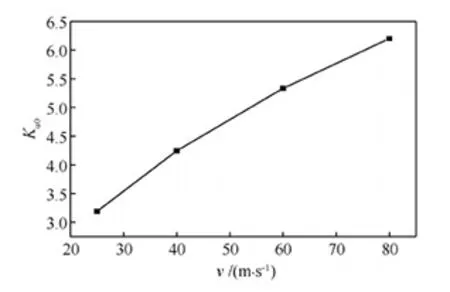
圖8 零迎角升阻比隨速度變化曲線 Fig.8 Lift-drag-ratio of 0° angle of attack curve vsvelocity

Table4Aerodynamicforceduetopower(CT=0.84,α=0°)

ΔCLΔCLincrement/%ΔCDΔCDincre?ment/%0．4876．90．1342170．9

表5氣動力系數增量分解(CT=0.84,α=0°)

Table5Decomposeofaerodynamiccoefficientsincrement(CT=0.84,α=0°)

CLaerCLpushCDaerCDpush0．28820．18910．02180．1123

動力增升所產生的氣動特性變化與飛機的構型密切相關。主要構型參數包括：發動機展向安裝位置、推力線安裝角度、發動機短艙的下沉量與前伸量、飛機前后緣襟翼形式及其偏角。這些參數直接影響噴流展向干擾因子、襟翼浸濕因子、發動機推力效率因子與動力產生的氣動力系數各分量所占比列。通過調整這些敏感構型參數，可以優化飛機起飛構型。

3.3 起飛場域性能評估

使用本文方法計算算例飛機在同一襟翼偏角的起飛滑跑距離Lrun，并與不考慮動力影響計算所得起飛滑跑距離進行對比，用于評估動力增升技術對起飛性能的影響。圖9與表6反映出外吹式襟翼動力增升飛機不同推重比T/W與不同起飛重量計算所得的起飛場域性能數據。

表6數據表明：動力增升技術對起飛滑跑距離性能收益ΔLrun隨起飛重量Wto與推重比非線性增大。當推重比為0.48時，算例飛機的起飛滑跑距離最大減小量可達到25%。

圖9 起飛性能收益隨推重比的變化曲線Fig.9 Takeoff performance curves vs thrust-weight ratio

表6 起飛重量對起飛滑跑距離的影響量Table 6 Takeoff running distance vs takeoff weight

3.4 起飛構型評估優化

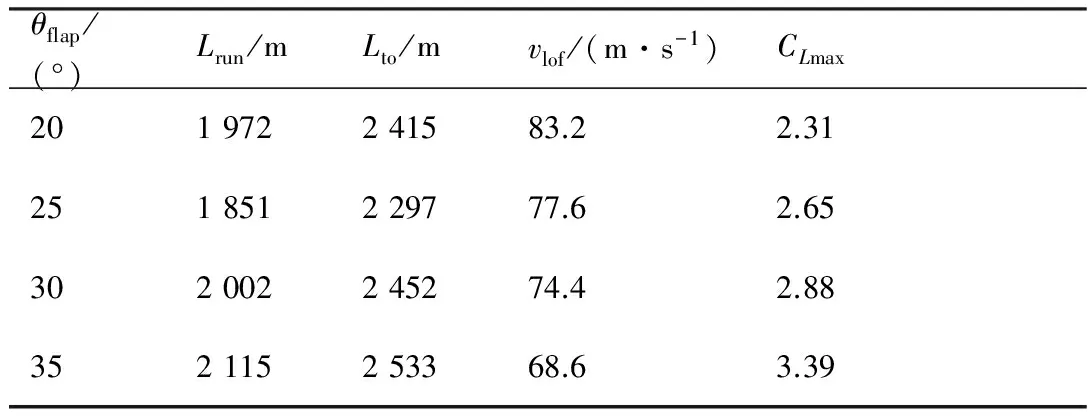
動力增升技術所帶來的氣動效益和性能收益與飛機構型密切相關。通過調整襟翼偏轉角，計算飛機不同襟翼偏轉角構型的氣動力與起飛場域性能，用以評估對象飛機起飛構型的優劣。表7給出飛機4款起飛構型的起飛性能計算結果，表中θflap為襟翼后緣上表面的下傾角。

表7數據表明：襟翼下偏25° 時，對象飛機起飛距離Lto最小。高速大型運輸機起飛構型襟翼偏轉角一般在30° 左右。動力增升飛機起飛構型襟翼偏轉角小于常規飛機，因為增大襟翼偏轉角，動力影響產生的阻力迅速增大，飛機的升阻比顯著減小，不利于縮短起飛滑跑距離。

表7多構型起飛性能計算數據

Table7Takeoffperformancecalculationdataofmulti-configuration

θflap/(°)Lrun/mLto/mvlof/(m·s-1)CLmax201972241583．22．31251851229777．62．65302002245274．42．88352115253368．63．39

4 結 論

1) 外吹式襟翼動力增升評估方法充分考慮了動力增升飛機的性能計算對氣動力的需求，解決了傳統推力系數法的使用限制問題。

2) 離地速度計算方法與性能計算中氣動力數據的使用方法，解決了工程應用中存在的問題，有效地提高了計算效率。

3) 優化運輸機的動力增升襟翼偏轉角，可有效地縮短起飛滑跑距離，改善起飛性能。

4) 增大推重比會使動力增升效應所獲得的性能收益增大。對于前線機場或高原機場，可通過減小起飛重量，增加性能收益來滿足起飛場域需求。

[1] PARLETT L P, SHIVERS J P. Wind-tunnel investigation of a large jet transport model equipped with an external-flow jet flap: AIAA-1968-4928[R]. Reston: AIAA, 1968.

[2] PARLETT L P, SHIVERS J P. Wind-tunnel investigation of an STOL aircraft configuration equipped with an external-flow jet flap: AIAA-1969-5364[R]. Reston: AIAA, 1969.

[3] PARLETT L P, FREEMAN D C. Wind-tunnel investigation of a jet transport airplane configuration with high thrust-weight ratio and an external-flow jet flap: AIAA-1970-6058[R]. Reston: AIAA, 1970.

[4] AOYAGI K, FALARSKI M D, KOENIG D G. Wind-tunnel investigation of a large scale 25 deg swept-wing jet transport model with an external blowing tripple-slotted flap: AIAA-1973-62197[R]. Reston: AIAA, 1973.

[5] BARBERIE F J, WICK A T, HOOKER J R. Low speed powered lift testing of a transonic cruise efficient STOL military transport: AIAA-2013-1099[R]. Reston: AIAA, 2013.

[6] WICK A T, HOOKER J R, BARBERIE F J. Powered lift CFD predictions of a transonic cruising STOL military transport: AIAA-2013-1098[R]. Reston: AIAA, 2013.

[7] MARCOS J, MARSHALL D D. Computational and experimental comparison of a powered lift, upper surface blowing configuration: AIAA-2010-0502[R]. Reston: AIAA, 2010.

[8] ENGLAR R J, CAMPBELL B A. Pneumatic channel wing power-lift advanced super-STOL aircraft: AIAA-2002-3275[R]. Reston: AIAA, 2002.

[9] 白俊強, 張曉亮, 劉楠. 考慮動力影響的大型運輸機增升構型氣動特性研究[J]. 空氣動力學學報, 2014, 32(4): 2-5.

BAI J Q, ZHANG X L, LIU N. The research of aerodynamic characteristics of high-lift configuration of large transport plane with the effect of engine jet[J]. Acta Aerodynamica Sinica, 2014, 32(4): 2-5 (in Chinese).

[10] 郭少杰, 王豪杰, 李杰. 外吹式襟翼動力增升數值模擬方法研究[J]. 航空工程進展, 2010, 1(1): 3-5.

GUO S J, WANG H J, LI J. Numerical simulating method for powered high-lift flow[J]. Advances in Aeronautical Science and Engineering, 2010, 1(1):3-5 (in Chinese).

[11] 李少飛, 李杰, 劉正賓. 外吹式襟翼動力增升繞流數值分析[J]. 航空計算技術, 2008, 38(5): 2-4.

LI S F, LI J, LIU Z B. Numerical simulation of externally blown flap with powered high-lift flow[J]. Aeronautical Computing Technique, 2008, 38(5): 2-4 (in Chinese).

[12] 劉李濤, 楊永, 李喜樂. 外吹式動力吹氣襟翼N-S方程數值分析[J]. 航空計算技術, 2008, 38(3): 2-6.

LIU L T, YANG Y, LI X L. Numerical analysis of high-lift system with externally blown flap using N-S equations[J]. Aeronautical Computing Technique, 2008, 38(3): 2-6 (in Chinese).

[13] SMITH C C. Effect of engine position and high-lift devices on aerodynamic characteristics of an external-flow jet-flap STOL model: AIAA-1971-6222[R]. Reston: AIAA, 1971.

[14] SMITH C C. Effect of wing aspect ratio and flap span on aerodynamic characteristics of an externally blown jet-flap STOL model: AIAA-1973-7205[R]. Reston: AIAA, 1973.

[15] JONES P K, BURGIN K. Conversion of lift coefficient increment due to flaps from full span to part span: ESDU-1974-74012[R]. London: ESDU, 1974.

[16] BONENFANT D, CARTER E C. Lift-curve slope and aerodynamic centre position of wings in inviscid subsonic flow: ESDU-1974-70011[R]. London: ESDU, 1974.

[17] WEIR J, FLOWER J W. Aircraft forces due to interference between a jet efflux and a slotted flap: ESDU-1982-82034[R]. London: ESDU, 1982.

[18] BOBBITT P J. Analysis of the takeoff and landing of powered lift aircraft: AIAA-2007-1273[R]. Reston: AIAA, 2007.

[19] BOBBITT P J, MARGASON R. Analysis of the take-off and landing of power-lift aircraft： AIAA-2007-1256[R]. Reston: AIAA, 2007.

[20] NORTON B. STOL Progenitors: The technology path to a large STOL aircraft and the C-17A: AIAA-2002-1369[R]. Reston: AIAA, 2002.

(責任編輯： 李明敏)

Method for evaluating powered high-lift effects ofexternally blown flap

ZHANGShengwei*,WANGWei

TheFirstAircraftInstituteofAVIC,Xi’an710089,China

Externally blown flaps are usually adopted to shorten the takeoff and land distance of transport aircrafts, and the method for evaluating the powered high-lift effect of the externally blown flap is one of the most important techniques in the design of transport aircrafts. A method for rapidly evaluating the powered high-lift effect of the externally blown flap is developed by coupling basic aerodynamics with the velocity correction technique. The proposed method takes into consideration the requirements for aerodynamic data in the performance computation of powered high-lift aircrafts, and can overcome disadvantages of classical trust coefficient method, such as low speed, limits of large thrust coefficient computation, low precision in solving unstick speed, and inefficiency of solving the problem of aerodynamic loading at multi-velocity point. The aerodynamic and takeoff performance of a transport aircraft are analyzed and the powered high-lift effects of the externally blown flaps are evaluated to validate the proposed method. The results show that the takeoff running distance can be shortened by 25% by deflecting the flaps rationally. However, with too large deflection angle of powered high-lift flaps, the aircraft drag will increase dramatically to go against shortening the takeoff running distance. The research results would provide some guidance for the design of externally blown flaps.

externally blown flap; powered high-lift; aerodynamics computation; performance earning evaluation; flap configuration optimization

2016-08-19；Revised2016-09-14；Accepted2016-10-10；Publishedonline2016-10-241051

2016-08-19；退修日期2016-09-14；錄用日期2016-10-10； < class="emphasis_bold">網絡出版時間

時間：2016-10-241051

www.cnki.net/kcms/detail/11.1929.V.20161024.1051.004.html

*

.E-mail13325381298@163.com

張聲偉， 王偉． 外吹式襟翼動力增升效果評估方法J． 航空學報,2017,38(6):220689.ZHANGSW,WANGW.Methodforevaluatingpoweredhigh-lifteffectsofexternallyblownflapJ.ActaAeronauticaetAstronauticaSinica,2017,38(6):220689.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0272

V211.12； V22.11

A

1000-6893(2017)06-220689-09

URL：www.cnki.net/kcms/detail/11.1929.V.20161024.1051.004.html

*Correspondingauthor.E-mail13325381298@163.com