基于諧響應分析的設備基礎設計方案優化

葉志雄 江勝學

基于諧響應分析的設備基礎設計方案優化

葉志雄 江勝學

（中鐵第四勘察設計院集團有限公司，430063，武漢//第一作者，高級工程師）

設備基礎通常要承受較大的動力荷載作用，但其振幅響應又不能過大。以某地鐵線路大型風機為例，基礎設計時考慮了5種方案。通過采用大型有限元計算軟件Ansys建立各種方案的有限元模型，同時考慮土-結構間的相互作用，進行多種土層參數情況下的動力特性及諧響應分析。通過對比基本方案的振幅計算結果與實測結果，證明了該分析方法的準確性。總結出了類似工程基礎設計時較為經濟有效的優化方向及優化原則。

設備基礎設計；土-結構相互作用；諧響應分析；設計優化

動力設備基礎主要有兩種，即大塊式或墻式基礎與框架式基礎。前者主要用于中、低轉速的機械；后者普遍用于高轉速的機器（≥3000 r/min）。這兩種動力設備基礎設計均以基礎的振幅越小越好為出發點，常用的分析方法有共振法和振幅法。振幅法直接控制振幅；共振法則通過控制基礎自振頻率避開共振區，以此來達到減小振幅的目的。

對于框架式基礎，國內已有了一定的研究。文獻［1］用單質點模型討論了壓縮機基礎動力參數出現偏差的原因。文獻［2］指出GB 50040—1996《動力機器基礎設計規范》推薦的簡化計算方法可能存在較大的誤差。文獻［3］對框架式汽機基礎進行了多方案的優化研究。文獻［4］研究了動力機械框架式基礎動力分析方法的適應性。而對于大塊式或墻式基礎，其相關的優化設計研究則較少。

本文結合某地鐵風機大塊式基礎的5種設計方案，通過大型有限元計算軟件Ansys建立了各種方案的實體有限元模型，并考慮土-結構間的相互作用，進行了多種土參數情況下的動力特性及諧響應分析。通過對比基本模型的振幅計算結果與實測結果，證明了該分析方法的準確性。對比分析各方案的計算結果，總結了有簡諧荷載作用的類似工程基礎設計時最經濟有效的優化方向及優化原則。

1 諧響應分析

諧響應分析是用于確定線性結構在承受隨時間按正弦（簡諧）規律變化載荷時的穩態響應的一種技術。該技術只計算結構的穩態受迫振動，而不考慮發生在激勵開始時的瞬態振動。通過諧響應分析預測結構的持續動力特性，從而驗證其設計能否成功地克服共振、疲勞以及其他受迫振動引起的有害效果。

諧響應分析是一種線性分析。任何非線性特性，如塑性和接觸單元將被忽略。該分析通常可采用4種方法：完全法（Full）、縮減法（Reduced）、模態疊加法（Mode Super position）及時程分析法。本文選用完全法進行分析。該方法采用完整的系統矩陣計算諧響應，同時用單一處理過程計算出所有的位移和應力。完全法允許在實體模型上施加各種類型的載荷（如節點力、外加的位移、單元載荷等），允許存在非對稱矩陣，且能考慮實體基礎與土彈簧間的相互作用。

2 項目概況和有限元模型

2.1 項目概況

某大型設備含有風機和電機，采用大塊混凝土基礎，混凝土材料為C25，基礎下設0.5 m厚的C10混凝土墊層。風機處于基礎中間，由旁邊的電動機通過軸承帶動，軸承固定在兩個止推上，如圖1所示。

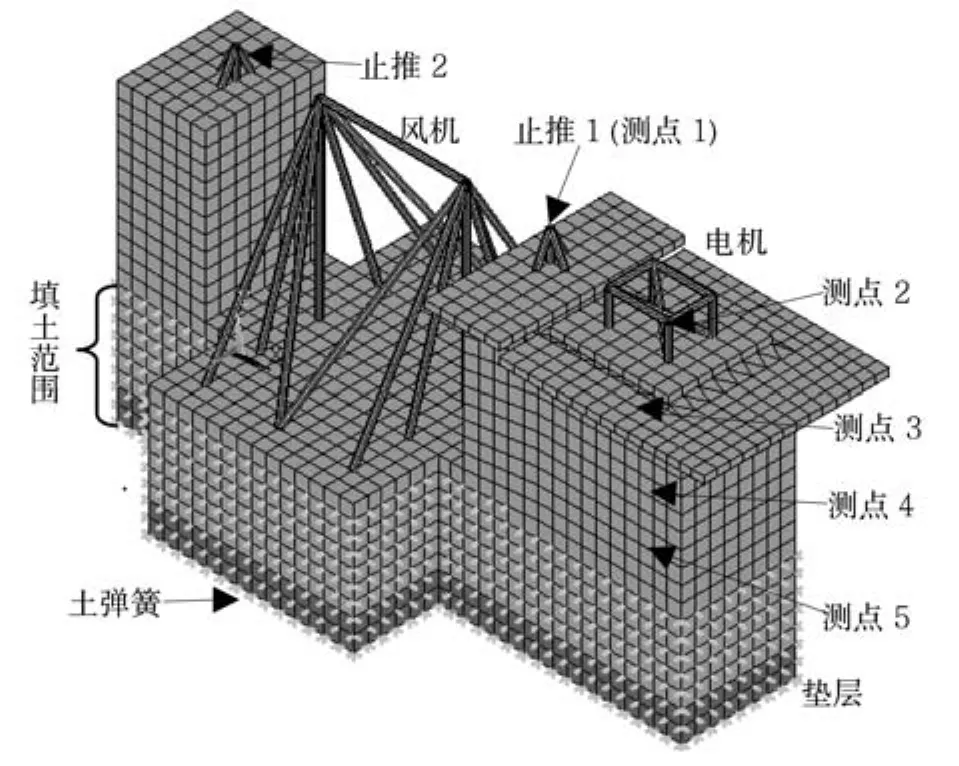
圖1 某大型設備基礎

在圖1中，電機（含止推1）的基礎寬2 m，長4.07 m，包含埋深在內的實體基礎高4.91 m；風機基礎寬4.74 m，長3.42 m，高2.15 m；端部止推2的基礎寬2 m，長1.89 m，高4.91 m。所有基礎連成一個整體，基本方案中基礎埋深為2 m。電機質量為8 200 kg；止推1的質量為6 200 kg；端部止推2的質量為6 000 kg；風機的質量為18 000 kg。

電機與風機的傳力軸承軸向為x向，豎向為y向，橫向為z向。設備運轉時，止推1、止推2以及風機對基礎有簡諧力作用。電機轉速為995 r/min。止推1施加給基礎的激勵力幅值為x向30.7 kN，z向69.9 kN，y向121.5 kN；止推2施加給基礎的激勵力幅值為x向 29.4 kN，z向67.6 kN，y向 117.6 kN；風機施加給基礎的激勵力幅值為x向88.2 kN，z向214.1 kN，y向352.8 kN。止推1、止推2及風機共用一個傳動軸承。根據實測，可不考慮3點激勵力的相位差。對于每個激勵點，x向激勵力與z向激勵力是同相位的，y向激勵力落后90°。混凝土基礎的持力層為粉土，由勘察資料可知不同深度土的豎向抗壓剛度系數Cu1、側向抗壓剛度系數Cu2、抗剪剛度系數Ct及阻尼系數。

2.2 有限元模型

采用大型有限元軟件Ansys建立該混凝土基礎的有限元模型。在該模型中，采用Solid 45塊單元模擬混凝土基礎；Combin 14單元模擬土層的影響，同時考慮土層參數隨深度而變化［5］；Mass 21單元模擬風機、電機的質量。文獻［6］未考慮風機、電機的剛度，但風機、電機的質心高度對基礎的動力特性會有較大影響。因此，采用Beam 188梁單元建立剛臂來模擬電機、風機質心高度的影響。剛臂一端連接風機、電機的質心，另一端連接風機、電機在基礎上的地腳螺栓。為解決Solid 45塊單元與Beam 188梁單元之間的自由度不匹配，采取多建一段Beam 188梁單元，使得梁單元與塊單元之間至少有2個以上節點共用。

本文采用集中質量法來模擬基礎與土體之間的相互作用。假定基礎周圍的土體是Winkler連續介質，結合半空間的Mindlin靜力基本解，將土體的質量按一定的厚度簡化并集中為一系列質點，并與基礎（樁基）之間用彈簧和阻尼器連接起來。即通過采用彈簧和阻尼器來模擬土體的動力性質，形成包括基礎（樁基）、土體的整體模型。

根據電機轉速，確定激勵力的頻率為：

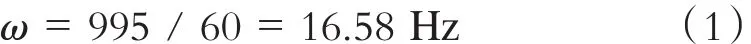
對風機與止推的質心施加諧荷載，先做模態分析，后用完全法進行諧響應分析，即可求得基礎在諧荷載激勵下的最大振幅。諧響應分析時，除了考慮土彈簧的阻尼外，全結構施加混凝土結構的阻尼比0.05。

該項目方案1（基本方案）（見圖1）為按規范進行的基礎設計，通過實測發現該方案下基礎的振幅偏大。故需對剩余未建造的基礎進行優化設計，優化時考慮以下4種方案。 方案2為去掉墊層方案，即去掉0.5 m厚的C10墊層；方案3為基礎補齊方案，即電機和止推在2.15 m高范圍內的基礎均補為4.74 m寬；方案4為加厚墊層方案，即將0.5 m厚的C10墊層優化為1.0 m厚C25墊層；方案5為加樁方案，即于基本方案的基礎周邊以每隔1 m的間距加C25短樁，短樁截面為300 mm×300 mm，樁長為2 m。

3 基本方案的計算結果

由地質勘察資料可知，持力層土經處理后實測抗壓剛度系數Cu=13.65 kg/cm3，抗剪剛度系數Ct=11.24 kg/cm3。基本方案中，基礎周圍10倍寬度和深度范圍內的土體可簡化為對應節點的集中質量；之后施加諧荷載激勵，進行諧響應分析。

對按基本方案的基礎共進行了7次振幅實測。實測結果表明，Z向振幅最大。將圖1中5個測點的計算結果與實測結果的平均值進行對比，如圖2所示。由圖2可知，計算結果與實測結果吻合較好，說明本文的有限元分析方法有很高的精確度。

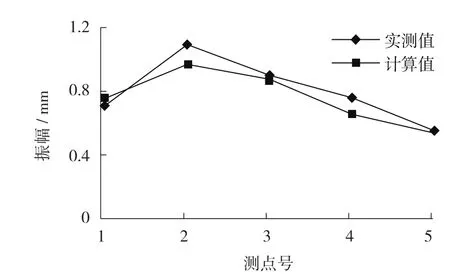
圖2 基本方案計算結果與實測結果對比

3.1 動力特性計算結果

考慮到實際工程中各測點的土參數有一定的離散性，故改變持力層土參數，對基本模型進行分析。其振動頻率隨Ct的變化如表1所示，隨Cu的變化如表2所示。

基本方案中第1階振動模態為z向對稱振動；第2階振動模態為y向反對稱振動；第3階振動模態為y向對稱振動。由表1可知，基本方案基礎的振動頻率隨Ct的變化很小，隨著Ct的增大，對應的每階振動頻率稍有增大；Ct在2 kg/cm3附近時，基礎第3階振動頻率接近激振力的頻率，從而使基礎振動不利。由表2可知，基本方案基礎的振動頻率隨Cu的變化較大，隨著Cu的增大，對應的每階振動頻率會增大；Cu增大到15 kg/cm3時，可能導致基礎第1階、第2階振動頻率接近激振力的頻率。

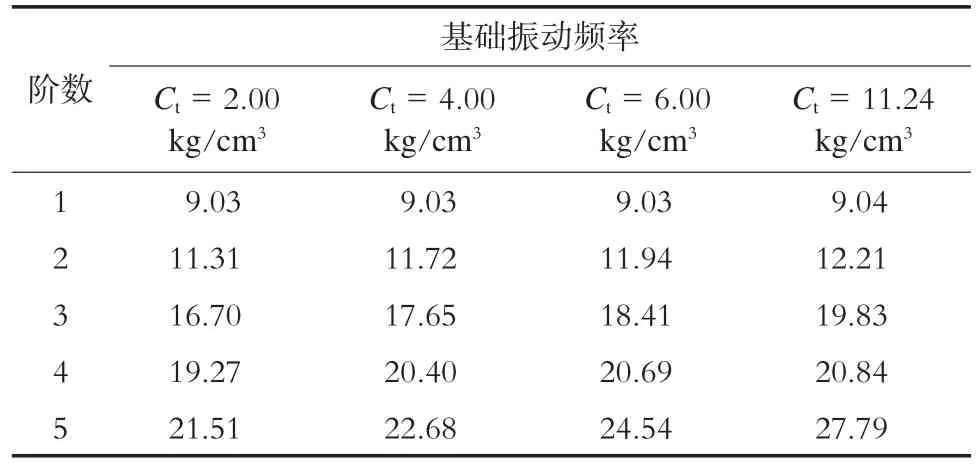
表1 Cu=13.65 kg/cm3時基礎振動頻率隨C t的變化Hz

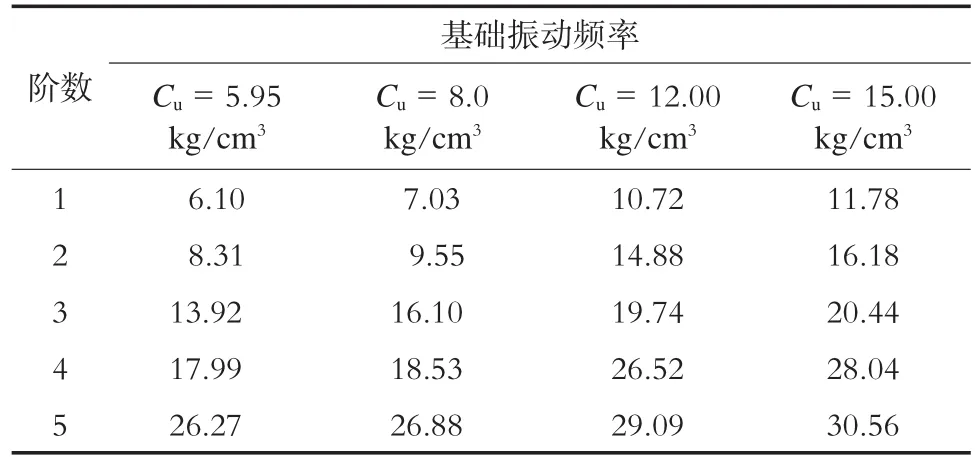
表2 Ct=11.24 kg/cm3時基礎振動頻率隨C u的變化Hz

因此，盲目地增大或者減小土的Cu和Ct，都有可能使得基礎的某階振動頻率接近激振頻率。故改變土層的參數需慎重。

3.2 振幅計算結果

通過改變持力層土的參數，對基本模型進行分析。其振幅隨Ct的變化情況如表3所示，隨Cu的變化情況如表4所示。

結合表3及表1可知，隨著Ct的增大，基礎的前幾階振動頻率逐漸遠離激振力頻率，基礎的Z向振幅逐漸降低，x向、y向振幅逐漸增大。這是因為，隨著振動頻率遠離激振力的頻率，第3階振型Z向擺動的主導作用在降低。

結合表4及表2可知，當模型的某階振動頻率接近激勵力的頻率時，基礎就會以這階頻率的模態為主導進行振動。如果這階模態為豎向振動，則出現豎向振幅大于橫向振幅的情況。

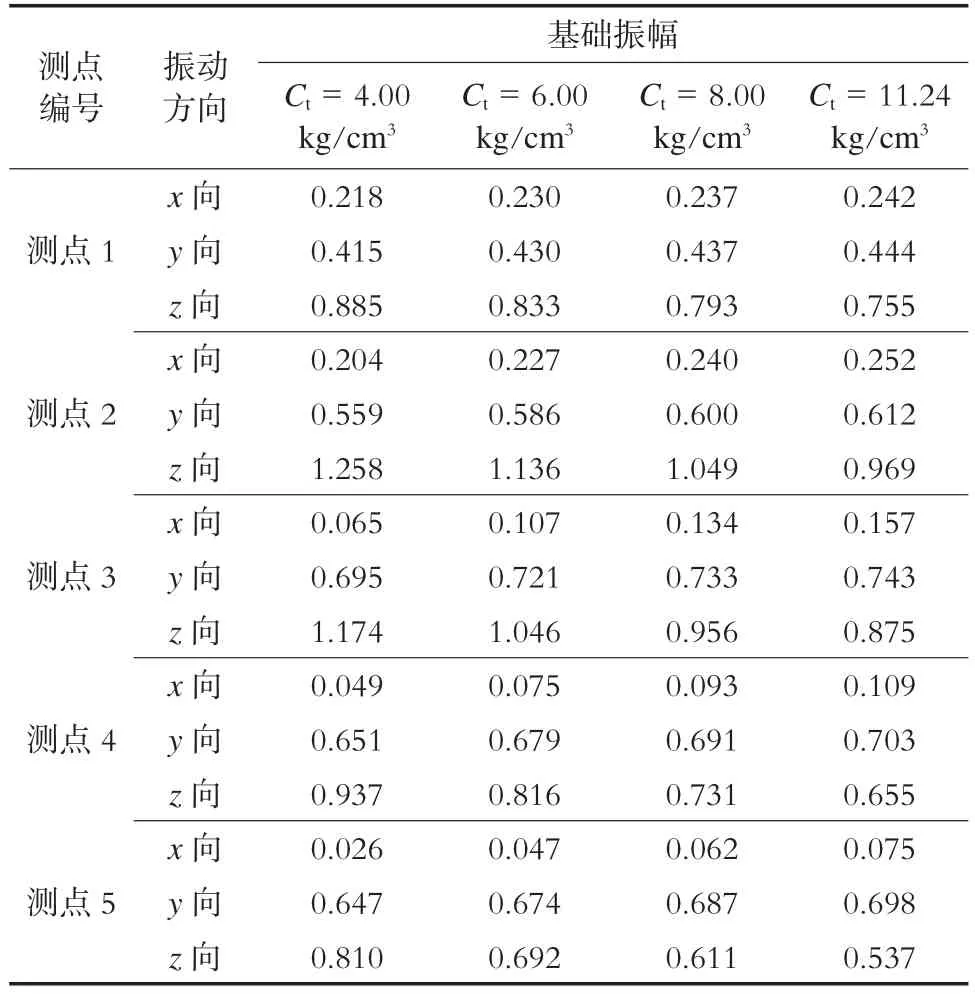
表3 Cu=13.65 kg/cm3時基礎振幅隨C t的變化 mm

表4 Ct=11.24 kg/cm3時基礎振幅隨C u的變化 mm

當 Cu=13.65 kg/cm3、Ct=4.0 kg/cm3時，基礎振動以第3階模態為主導，如圖3所示。

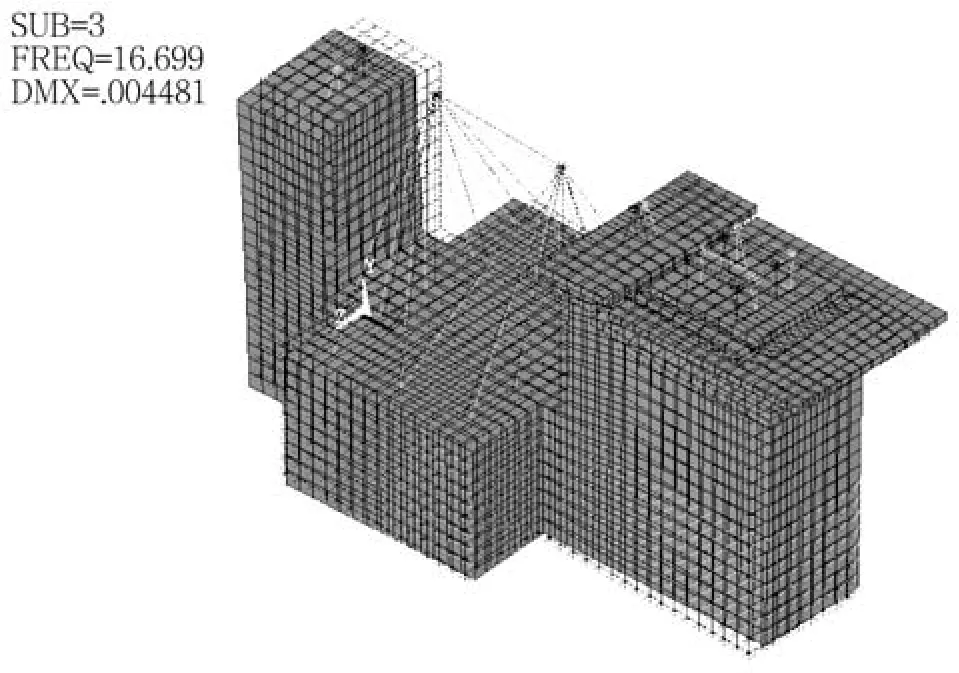
圖3 基礎第3階振動模態

此外，對基本模型還計算了改變阻尼比的情況，結果表明振幅響應變化很小。

4 優化方案的計算結果

考慮到土層參數的改變難以做到精確控制，且土層參數離散對計算結果的影響比較大。因此，基本方案的優化主要從改變基礎自身振動特性出發。考慮到實際工程中，Cu一般變化較小，而Ct會隨著場地各點的土層厚度而變化。因此，通過考慮Ct的變化對優化方案進行分析。

4.1 動力特性計算結果

當 Cu=13.65 kg/cm3、 Ct=11.24 kg/cm3時，各方案的振動頻率比較如表5所示；當Cu=13.65 kg/cm3、Ct=6.00 kg/cm3時，各方案的振動頻率比較如表6所示。

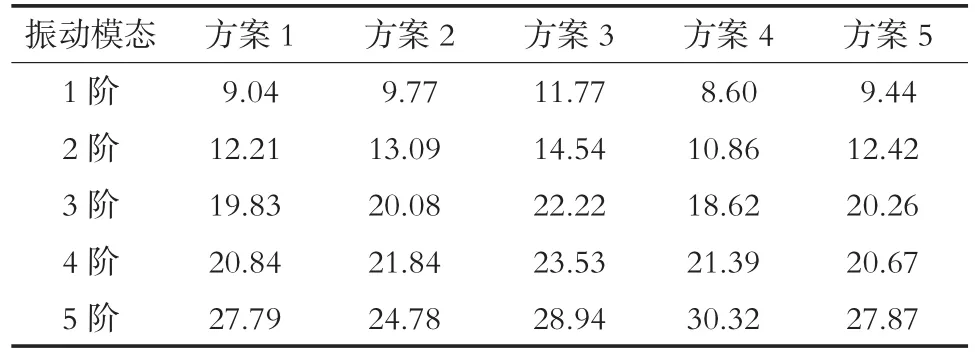
表5 各方案的振動頻率比較 Hz

表6 各方案振動頻率比較 Hz

由表5及表6可知，方案3及方案4的各階振動頻率計算結果與激勵力的頻率偏離較大，且其在Ct變化時變化亦很小，具有較好的適用性。

4.2 振幅計算結果

由于測點1和測點3具有代表性，故文中僅列出這2個測點對應位置的計算結果。測點1的計算結果如表7所示，測點3的計算結果如表8所示。由表7及表8可知，方案3及方案4的振幅計算結果比方案1有較大減小，并在Ct變化時具有較好的適用性。而方案2的振幅比方案1有所增大。

5 計算結果對比分析

（1）方案2與方案1相比，前3階振動模態沒有變化，各階振動頻率有增大。其中，第2階振動頻率趨于靠近激勵力的頻率，振幅稍有增大，振幅隨土層參數的變化規律沒有改變。因此，去掉墊層是不合適的。

（2）方案3與方案1相比，基礎的振動模態發生變化，第3階為z向反對稱振動。其中，第2階振動頻率趨于靠近激勵力的頻率，然而其第2階振型是豎向振動為主，使得其在激勵力作用下z向振幅與方案1相比有減小。

（3）方案4與方案1相比，振動模態沒有變化。

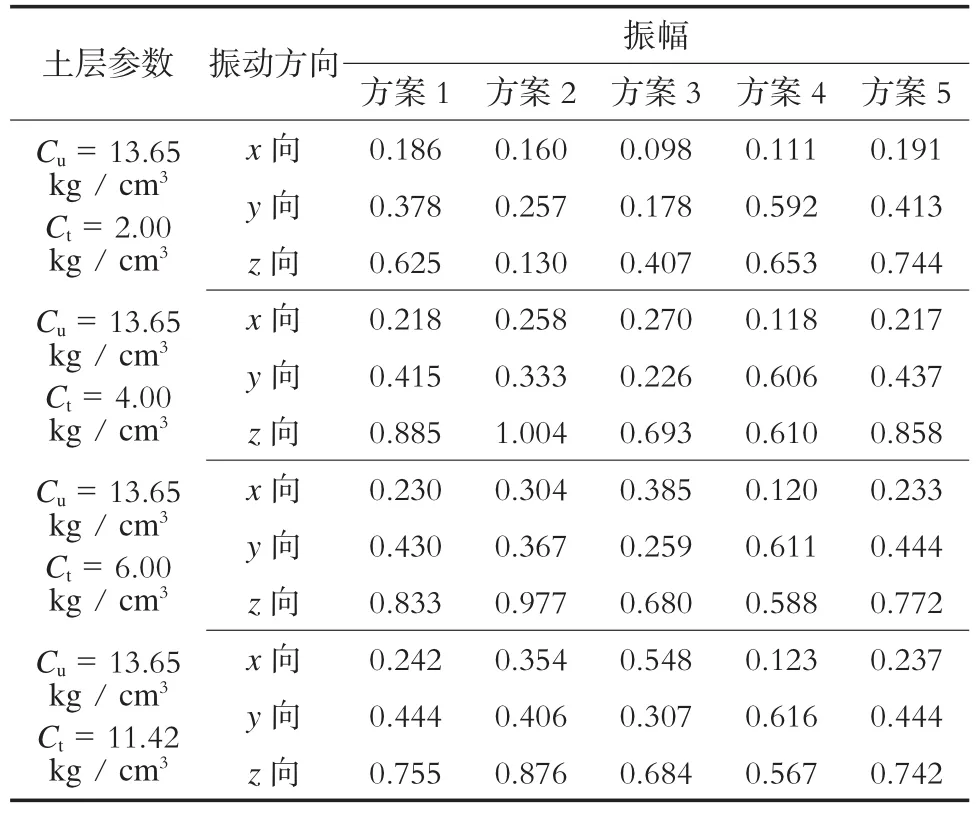
表7 各方案測點1的振幅 mm

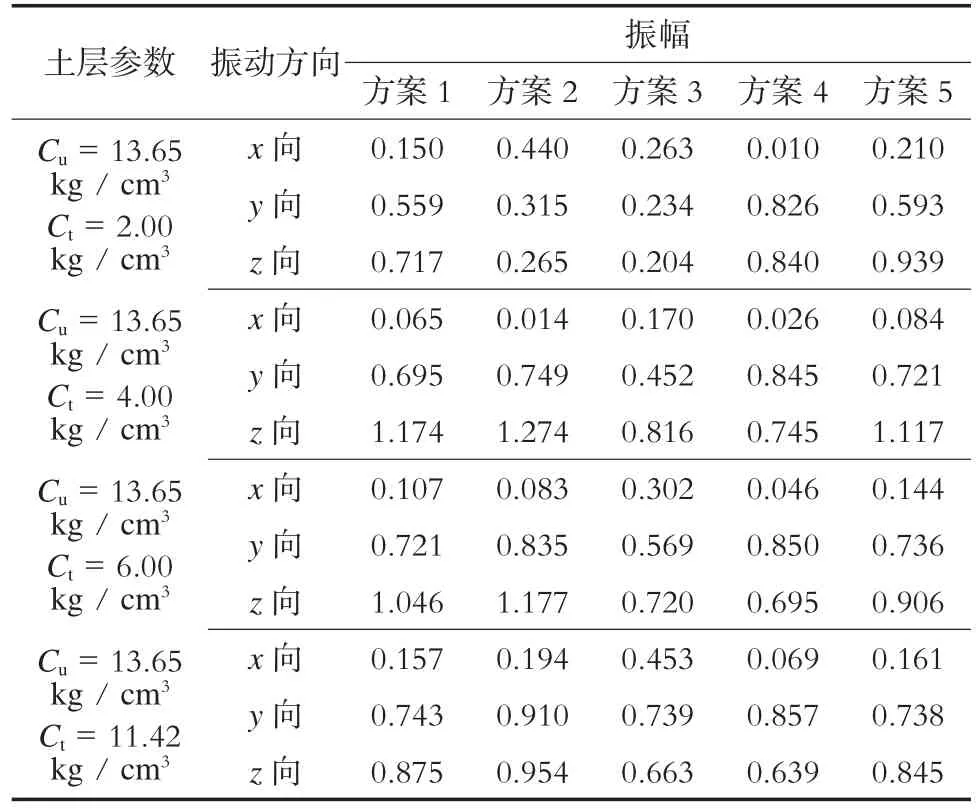
表8 各方案測點3的振幅 mm

其中，第2階振動頻率趨于遠離激勵力的頻率，雖第3階振動頻率稍微靠近激勵力的頻率，且第3階振型是豎向振動為主，使得該方案的z向振幅有較大的減小、y向振幅稍有增大。該方案隨土層的參數變化，其振動頻率變化很小，不會出現過于接近激勵力頻率的情況。

（4）方案5與方案1相比，基礎的振動模態發生變化，第3階為z向反對稱振動。其z向振幅與方案1相比稍有減小，但減小不明顯。

綜合以上分析，對于該設備基礎，方案4為最優方案。因此，建議后期建設的設備基礎均按方案4進行施工。

6 結論

本文通過對某大型設備基礎進行多方案優化設計分析，得到以下結論：

（1）實體有限元方法能較好地模擬土與結構的相互作用，有較高的計算精度。準確計算設備基礎的各階振動頻率和模態很重要，不建議使用文獻［7］簡化為單質點的計算方法。

（2）基礎振動與基礎自身頻率、激勵力頻率緊密相關。當基礎所有模態對應的振動頻率都離激勵力頻率較遠時，基礎振動形式以第1階振動模態為主導。當基礎某階振動頻率與激勵力頻率接近時（相差小于1 Hz），基礎振動形式則以這階振動頻率對應的振動模態為主導，且其頻率相差越小，基礎振幅越大。

（3）設備基礎的設計優化原則為：盡量使基礎各階振動頻率均遠離激勵力的頻率；特別注意可能會出現前1階振動頻率避開了，而后1階振動頻率更加接近激勵力頻率的情況；單純增加基礎質量不一定合適，具體問題需要具體分析。

（4）設備基礎設計時，應考慮土層參數的離散性。勘察時應盡量測得建設場地詳細的、準確的土層參數。也可以選擇對土層參數的變化有較好適應性的設計方案。

［1］ 裴欲曉，張克峰，戴康德.大型活塞式壓縮機基礎的動力分析及設計［J］.建筑結構，2003，33（11）：36-38.

［2］ 孔垂燭，薛尚鈴，尹菊麗.某動力機器基礎動力學分析［J］.巖土工程技術，2007，21（5）：254-256.

［3］ 代澤兵，劉寶泉，吉曄，等.1000 MW汽機基礎動力特性優化［J］.武漢大學學報（工學版），2008，41（S）：145-148.

［4］ 袁金秀，王道遠，陳春雷.動力機器框架式基礎動力分析方法的適應性研究［J］.石家莊鐵道學院學報（自然科學版），2009，22（4）：82-85.

［5］ 劉晶波，王振宇，張克峰，等.考慮土-結構相互作用大型動力機器基礎三維有限元分析［J］.工程力學，2002，19（3）：34-38.

［6］ 周慧，樊健生，聶建國，等.設備剛度在大型汽輪發電機框架式基礎動力分析中的處理方法［J］.武漢大學學報（工學版），2009，42（S）：470-473.

［7］ 國家技術監督局.中華人民共和國建設部.動力機器基礎設計規范：GB 50040—96［S］.北京：中國計劃出版社，1997：1.

Design Optimization of Metro Equipment Foundation Based on Harmonic Response Analysis

YE Zhixiong，JIANG Shengxue

Equipment foundation generally needs to bear larger hydrodynamic load，but large amplitude response is not permitted.Taking a large fan foundation on metro line as an example，five different schemes are considered in the foundation design.Large finite element Ansys software is used to establish models for various schemes，with full consideration of the interaction between soil and structure，the dynamic properties and harmonic response are calculated in condition of various soil parameters.The amplitude calculation results of the basic scheme are compared with measured data，the accuracy of this analysis method is proved.At last，effective optimization direction and optimization principles for similar projects are summarized.

equipment foundation design；soil-structure interaction； harmonic response analysis； equipment design optimization

TU476+.1

10.16037/j.1007-869x.2017.10.027

Author′s address China Railway Siyuan Survey And Design Group Co.，LTD.，430063，Wuhan，China

2016-01-21）