基于聚類狀態主控邊界點的單調多態關聯系統可靠性分析

張永進， 孫有朝， 張燕軍

1.安徽工業大學 數理科學與工程學院， 馬鞍山 243002 2.南京航空航天大學 民航學院， 南京 211106 3.揚州大學 機械工程學院， 揚州 225127

基于聚類狀態主控邊界點的單調多態關聯系統可靠性分析

張永進1， 孫有朝2,*， 張燕軍3

1.安徽工業大學 數理科學與工程學院， 馬鞍山 243002 2.南京航空航天大學 民航學院， 南京 211106 3.揚州大學 機械工程學院， 揚州 225127

鑒于組成系統單元的多狀態單調關聯性特征，將多元離散函數理論引入描述系統狀態結構函數，發展了控制狀態等價類主導狀態向量的狀態等價類主控邊界點的邏輯方法，推導了多態單調關聯系統的狀態結構函數、可靠性和期望狀態表達式；面向顧客的需求偏好，將負效用函數嵌入系統平均性能效用模型；鑒于元件狀態引起的計算復雜性，提出了集合運算的德摩根律法和新型的框圖式算法，簡化了系統可靠度的表達式。結合某型航空發動機的簡化演算，驗證了主導等價類向量方法和框圖算法的合理性與有效性，為工程系統的可靠性設計和可靠性管理提供理論依據。

主控邊界點； 離散函數； 多狀態關聯系統； 單調性； 可靠性

隨著系統設計的結構越來越復雜化，組成單元從“完美工作狀態”到“完全失效狀態”的演化過程中往往會經歷若干中間狀態，而系統的狀態取決于系統內部若干個元件提供的狀態組合，從而系統表現出多狀態特征，它是工程機械系統性能的重要表征，如鍋爐燃燒的燃油量由若干噴油器噴出，汽輪機所需蒸汽量由若干鍋爐提供等。隨著多態系統研究的深入，工程上提出系統中任何一個元件都有其特定的功能，而且一個部件質量的改善不會降低系統的可靠性[1]，這就使得單調關聯多態系統(Multi-State Coherent System：MSCS)的可靠性研究具有重要的現實意義。

最早Barlow[2]和EI-Neweihi[3]等對多態關聯系統進行了研究，對多態關聯系統給出了一系列基本定義，隨后Natring[4]進一步完善了多態關聯系統基本概念。目前，常見關于多態關聯系統的可靠性研究方法有多狀態故障樹[5-6]、系統結構函數[7]、多狀態最小路與割[8-13]、齊次馬爾可夫模型[14-15]、非齊次馬爾可夫模型[16]、隨機衰退模型[17-18]、通用生成函數[19]和壽命分布函數[20]等方法，這些方法中多數并不考慮面向使用者的系統效能。進一步，系統可靠性評估通常建立在子單元可靠性數據的基礎上，為此Barlow和Wu[2]將二態關聯系統的可靠性理論推廣到多態關聯系統，EI-Neweihi[3]獲得了系統性能與部件性能之間的關系，分別給出了一個并聯系統和一個串聯系統中存在的可靠性上下邊界，Kundu[21]和Franko[22]等研究了單調關聯系統可靠性問題。考慮部件性能改進對系統性能改進的影響，Griffith[23]給出了一個多態系統結構函數公理化方法，考慮系統效用，得到了系統性能度量方法。基于最小路和最小割原理，Butler[24]提出用模塊分解方法來改進多態系統的可靠性邊界，并研究了可靠性界限。為研究關聯系統結構特性，Block和Savits[25]推導了多態系統結構函數的分解理論，給出了系統元件關聯性與重要性基本概念。面向顧客偏好的多態關聯系統，Hudson與Kapur[26]首次提出了等價類和邊界點基本概念，分析了系統所處固定狀態的概率，應用容斥原理和不交集對系統可靠性的狀態邊界進行了改進。基于顧客對系統元件狀態變化如何影響系統狀態的陳述，Boedigheimer和Kapur[7]建立了顧客偏好下系統的結構函數，給出了系統處于指定狀態的概率計算方法。應用等價類和邊界點結構函數方法，Lisnianski與Levitin[27]對系統可靠性性能進行了分析。鑒于結構函數描述系統狀態的有效性，Liu[28]和Magana[29]等進一步完善了等價類結構函數評估系統可靠性的方法，建立了多態單調關聯系統的結構函數，應用最小路和最小割方法研究了系統可靠性，然而隨著單元數以及元件狀態數的增加，計算復雜性也快速增加。

針對工程中常見的多狀態單調關聯系統，本文擬應用結構函數與離散函數相關理論，基于Lisnianski[27]、Liu[30]以及Magana[29]等給出的系統狀態等價類及邊界點方法，將一般狀態等價類推廣到可靠的狀態聚類，應用狀態等價聚類的邊界點方法對多態關聯系統可靠性進行研究，提出基于邏輯代數的德摩根律方法以及簡易框圖算法，優化計算復雜程度。最后給出一個算例分析，將航空發動機系統分解成一般性可靠性框圖結構，分析該系統所處的各個狀態時的可靠度，驗證所給出的新方法的有效性，為工程實際的復雜多態關聯系統可靠性設計提供理論基礎。

1 單調多態關聯系統

考慮一個含有n個元件的單調MSCS。設一個多態系統具有M+1個狀態，不妨記為狀態集{0,1,…,M}，設該系統由n個元件構成，而且這些元件具有多個狀態，記為{0,1,…,mi}(i=1,2,…,n)，即元件共有mi+1個狀態。若一個系統具有初始性能狀態，并非完好狀態時，不妨記這些狀態為{l,l-1,…,l-k+1}?{0,1,…,M}，其中l-k+1為系統的最低可用狀態，l為系統初始狀態，k為任意狀態。

由于一個系統所處狀態總是由其組成元件的狀態所確定，不妨記xi為第i個元件所處狀態，即xi∈{0,1,…,mi}，于是系統所有元件狀態構成一個狀態向量x=[x1,x2,…,xn]，則一定存在一個系統狀態s∈{0,1,…,M}及從部件狀態到系統狀態的映射φ，滿足

φ(x)=s

φ:[0,1,…,m1]·…·[0,1,…,mn]→

[0,1,…,M]

稱φ為系統狀態的結構函數。

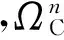
x=[x1,x2,…,xn]

ΩCi∈{0,1,…,mi}，ΩS∈{0,1,…,M}

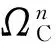
(0,1,…,mn)

為方便構建多狀態單調關聯系統的結構函數φ(x)，首先給出狀態向量序概念。

定義1設x=[x1,x2,…,xn]，y=[y1,y2,…,yn]是2個元件的狀態向量。若單元狀態向量滿足“xi>yi且至少存在一個元件i滿足xi>yi(i=1,2,…,n)”，則狀態向量x優于狀態向量y，記作x?y。

下面給出MSCS的數學定義及性質[31]。

定義2對于一個由n個元件構成的多狀態系統{C,φ}，其中C表示元件，記xi和yi是系統第i個元件所處的狀態，則有

① 規范性(邊界條件)。若系統所有部件失效，則系統處于完全失效狀態；若系統所有部件處于完美狀態，則系統處于完美狀態，即有

φ(0,0,…,0)=0，φ(m1,m2,…,mn)=M

② 可達性。對于系統的每一個狀態k，至少有一個部件狀態向量x=[x1,x2,…,xn]滿足

φ(x)=φ(x1,x2,…,xn)=k∈{0,1,…,M}。

③ 關聯性。系統中每個元件均具有其特定作用，不存在無關元件，即系統中不存在不關聯元件。若標記元件狀態向量

(αi,x)=(x1,x2,…,xi-1,αi,xi+1,…,xn)

(βi,x)=(x1,x2,…,xi-1,βi,xi+1,…,xn)

則關聯性應用數學方法可描述為：若αi≠βi，則φ(αi,x)≠φ(βi,x)。

④ 單調性。部件性能改進不會導致系統性能惡化，即系統元件的狀態函數φ(x)是單調增的。若2個部件狀態向量滿足序x?y，則系統狀態向量滿足φ(x)>φ(y)；若向量序x≤y，則系統狀態向量滿足φ(x)≤φ(y)。

通常，滿足上述性質的系統{C,φ}稱為多狀態單調關聯系統，結構函數φ(x)為單調關聯結構函數。

2 可靠狀態類與邊界

考察系統所處狀態的性能水平，需要分析對應系統性能水平下部件的狀態組合，由于不同的部件狀態組合可能使得系統性能處于同一個狀態水平，從而需要找到同一個系統水平下各個不同元件所處狀態的集合類，即狀態等價類。不妨將部件狀態向量空間劃分為一系列等價類，每個等價類對應于系統的特定狀態。

定義3對于系統的任意狀態k，稱集合

k∈{0,1,…,M}

為系統狀態等價類。

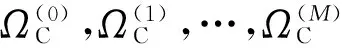
不同顧客對象對于系統性能水平的要求不同，多態關聯系統的可靠性可以理解為系統所處的狀態不低于系統規定的性能狀態。鑒于此，應用定義3從面向顧客要求的性能水平角度給出多態系統的可靠狀態等價類定義4。

定義4對于規定的系統最低可靠性狀態k，標記系統狀態不低于k的元件狀態集合表示為等價類

k∈{0,1,…,M}

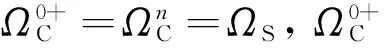
由于給出的等價類分類中元素隨著組成部件的增加會快速增加，為方便計算，下面給出主導每一個等價類中的邊界元素定義。

根據狀態等價類定義知，任一個可靠等價類可能包含不止一個狀態組合，而且可能有些狀態組合對系統可靠性評估計算時是冗余的，導致在系統結構函數的簡化過程中會出現無關的元件狀態向量，為此給出控制狀態類的邊界。

{φ(y)}max=k-1

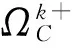
基于已給出的假設和定義，多態單調關聯系統在水平k時的可靠性可表示為

根據定義5給出的主控邊界點定義，表明邊界點的作用是用較少的等價類元素控制和主導等價類中其他元素，避免重復計算而使得計算量大大減少。

3 單調MSCS可靠性

要獲取單調關聯多態系統的結構函數，需要將二元邏輯運算擴展到多元邏輯運算，利用離散函數相關定義，首先給出邏輯運算的析取形式。

3.1 離散函數析取運算式

根據離散函數的析取運算，對于任意實數u和v，二元邏輯運算可以被延伸為下述析取運算形式：

u∪v=max(u,v)

為了將邏輯運算應用于多狀態變量，需要將二元邏輯運算擴展到n元邏輯運算，下面給出二元變量集合運算{u1,u2,…,un}為

對于一個二元系統，考慮系統元件只有2個狀態，若二元部件“成功”，則xi取值1，否則取值0，從而對應的指示函數I(xi=1)=xi，否則I(xi=0)=1-xi。于是根據樞軸量分解式，元件i的結構函數φ(x)可表示為“析取”范式形式：

φ(x)=xiφ(1i,x)+(1-xi)φ(0i,x)=

I(xi=1)φ(1i,x)+I(xi=0)φ(0i,x)=

(1)

式中：1i和0i表示第i個元素取值為1和0；若xi=α，則指示變量I(xi=α)=1，否則指示變量I(xi=α)=0。

從而根據式(1)，多狀態系統的結構函數樞軸量分解可以表示為如下“析取”范式形式[26]：

(2)

式中：元件i的最低狀態為0，最高狀態為mi。顯然，式(2)給出了單個元件的結構函數“析取”形式，于是對于一個由n個子單元構成的多態單調關聯系統而言，根據定義5，其結構函數樞軸分解可以表示為“析取”范式形式[26]：

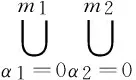
(3)

顯然式(3)給出了一個多態系統結構函數表示形式，但隨著狀態數目的增加，結構函數的復雜程度會快速增加。

3.2 邊界點結構函數

從式(3)知，若要計算一個單調關聯多態系統結構函數，需要計算所有可能組合表達式，這是極其繁瑣的，需要尋找新方法優化結構函數，為此將最小路集基本概念推廣到MSCS，給出MSCS的最小路結構函數表示形式。

一個最小路集是一個確保系統正常工作的最少部件集合。一個系統通常有多個最小路集，不妨標記Pj是該系統的第j個最小路，j=1,2,…,p，p為系統的最小路集數，則一個二元關聯系統結構函數可表示為

j=1,2,…,p

記最小路集中所有的部件正常取值1，否則取值為0。由于一個系統正常運行的充要條件是至少有一個最小路中所有部件正常運行，從而該系統的二元結構函數可表示為

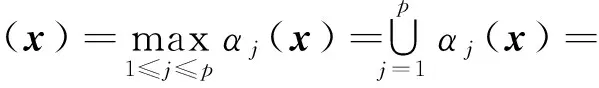
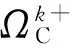
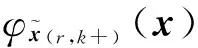
(4)

(5)

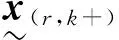
若將各個下邊界點的結構函數式(5)代入系統的結構函數式(4)，可以得到MSCS的結構函數形式為

(6)

式(6)為使用邊界點的系統結構函數，通過使用第i個子單元狀態與邊界點中第i個元素進行邏輯比較，獲取指示函數值。

為便于邏輯代數運算，可利用德摩根律，將式(6)重新表示和描述。首先不妨引入記號：

(x1x2…xn)

則式(6)可表示為

為求MSCS的可靠性，Lisnianski[27]和Liu[30]等給出了系統狀態等價類的邊界問題，以下簡記為L-L方法,該方法的結構函數形式為

(7)

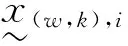
3.3 MSCS可靠度計算

對于一個MSCS，其可靠性可定義為在指定的時間和環境條件下，系統在一個指定或更高狀態下執行任務的概率，從而MSCS以狀態k或更高狀態執行任務的可靠性可表示為

Rk=Pr{φ(x)≥k}=

X2=s2,…,Xn=sn}·

Pr(X1=s1,X2=s2,…,Xn=sn)=

Pr(X1=s1,X2=s2，…,Xn=sn)=

E{I[φ(x)≥k]}

(8)

式中：k=0,1,…,M，si∈{0,1,…,mi}，指示變量

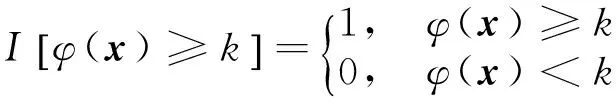
若部件壽命具有統計獨立性，則有

(9)

由式(8)可以觀察到，計算Rk需要計算所有向量下的系統結構函數，隨著系統狀態的增加復雜程度快速增加。若應用式的最小析取范式，MSCS的可靠性計算會有所簡化。

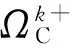
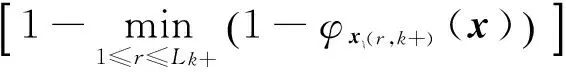
若給出運算標記

則上述可靠度計算式可重新分別簡記為

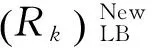
(10)

顯然，在式(10)的運算過程中，需要用到2個指示函數乘積問題。為計算Rk，首先給出其運算規律：

I(xi≥u)·I(xi≥v)=I(xi≥max(u,v))

(11)

式中：u和v是實數。基于規則式(11)，指示函數連乘的期望運算為

(12)

式中：pi,si為第i個元件處于狀態si的概率。將式(11)、式(12)代入式(10)，系統處于不低于狀態k下運行的可靠性Rk可通過式(13)進行計算：

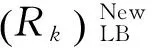
(13)

而應用L-L方法，基于邊界點計算系統處于狀態k運行的可靠性表達式為

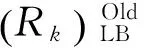
(14)

3.4 系統性能效用

對于系統設計者和使用者而言，多態系統處于某一個狀態時的概率具有重要指導意義。根據式(13)和式(14)，系統處于某個固定狀態k時的可靠性可表示為

Pr{φ(x)=k}=Rk-Rk+1

(15)

進一步，根據系統所處每一個狀態的概率，系統所處平均狀態可表示為

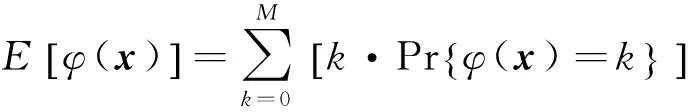
(16)

事實上，系統開始進入使用或貯存時的可靠性可表示為R0=Pr{φ(x)=M}=RM，從而若此多狀態系統處于狀態k時的可靠度包含有初始可靠性，那么系統僅僅因為本次使用或貯存而產生的可靠度可表示為

工程上，一個負效用函數可以衡量顧客偏好下的效用損失，經濟損失與系統完美性能和當前狀態差量密切相關，即若一個系統在最佳狀態時，則顧客的負效用度達到最低。通常應用一個指數負效用函數去度量這種關系[29]：

DU[Δ(x)]=ρ[eβ(M-φ(x))-1]

式中：ρ、β為系統退化參數。當系統處于完美工作狀態時，負效用值等于0；當系統完全失效時，系統負效用值為ρ[exp(βM)-1]。應用該函數可以計算出該系統的期望負效用值，具體為

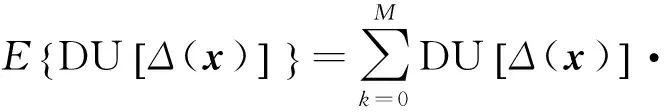
Pr{M-φ(x)=k}=ρ·

(17)

事實上，式(17)的負效用能夠刻畫顧客角度的不滿意程度，對于復雜系統可靠性設計具有一定的指導意義。

4 算例分析

下面給出一個某型號航空發動機系統的算例分析，考慮該整機系統有多個狀態，其子系統也具有多個狀態，應用本文提出的方法計算系統的可靠性。某型號雙轉子航空發動機系統結構如圖1所示。

根據圖1(d)中可靠性框圖，假設各個單元狀態列于表1～表4,x1、x2、x3和x4分別為系統各單元所處狀態，根據這些子單元狀態，驗證所提出方法和原始方法的算法比較。

在航空發動機系統中，表征壓氣機性能好壞的主要參數有[32]：空氣流量、增壓比、效率和喘振裕度。由于增壓比為壓氣機出口氣流壓強與其進口氣流的壓強之比，總增壓比的高低，在設計時根據特定型號發動機的需要來確定，它是影響渦輪噴氣發動機工作性能的一個重要的循環參數，對發動機的單位推力和耗油率有較大的影響。工程上，總增壓比越高，發動機性能就越好(推重比大、耗油率低)。考慮某先進軍用渦輪噴氣發動機的總增壓比為8～12，給出狀態分類如表1所示。

由于發動機的燃燒室的功能是把燃料的化學能給釋放出來，轉換為熱能，使氣體的總焓增大，提高燃氣的膨脹做功能力，其狀態好壞，直接影響發動機的工作性能。而燃燒室主要由主燃燒室和加力燃燒室構成，主燃燒室位于壓氣機和渦輪之間，而加力燃燒室位于渦輪后噴管前，是為較短時間內增大發動機推力而設置的[32]。下面就燃燒室工作原理，將這一部分分成2個子單元(主燃燒單元B1，加力燃燒單元B2，如圖1(b)和圖1(d))所示，根據點火可靠、燃燒穩定與燃燒完全等劃分為3個狀態，具體數據見表2和表3。

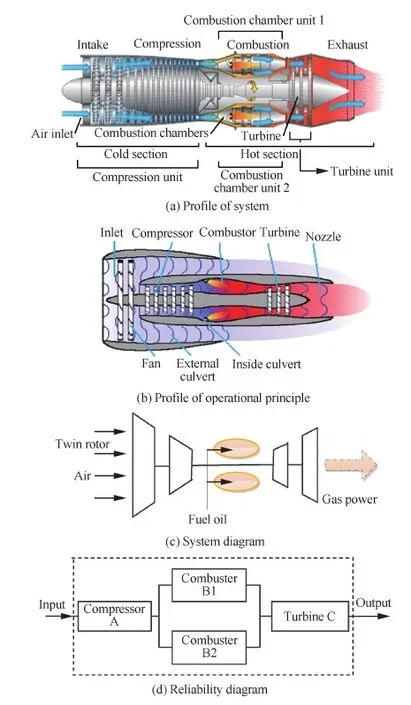
圖1 雙轉子航空發動機系統Fig.1 Twin-rotor aero engine system

渦輪的主要目的是將氣流的能量轉換為機械能，高溫高壓燃氣在渦輪內膨脹，向外輸出功帶動壓氣機，氣流流過時產生作用力，對轉子葉片作功使其轉動，而將氣流的能量轉換成機械能輸出[32]。由于渦輪轉子葉片是在高溫燃氣包圍下工作，不僅承受自身氣動力、離心力、熱應力和振動應力等作用，而且要抵制高溫燃氣的沖刷、氧化與腐蝕作用，從而產生磨損、腐蝕和高溫氧化等表面失效，以及蠕變、高低周疲勞斷裂等整體失效模式，于是渦輪轉子葉片的工作狀況對航空發動機的運行性能與可靠性起著決定性作用。根據這些失效模式和機理，考慮渦輪轉子具有4個不同狀態。

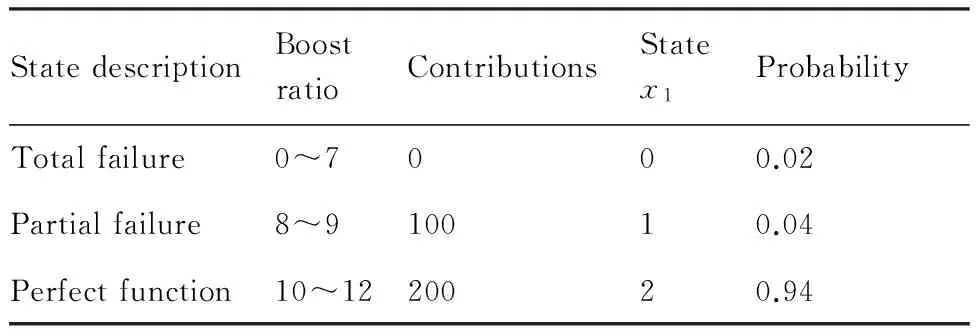
表1 壓氣機單元A狀態概率Table 1 State probability of compressor A

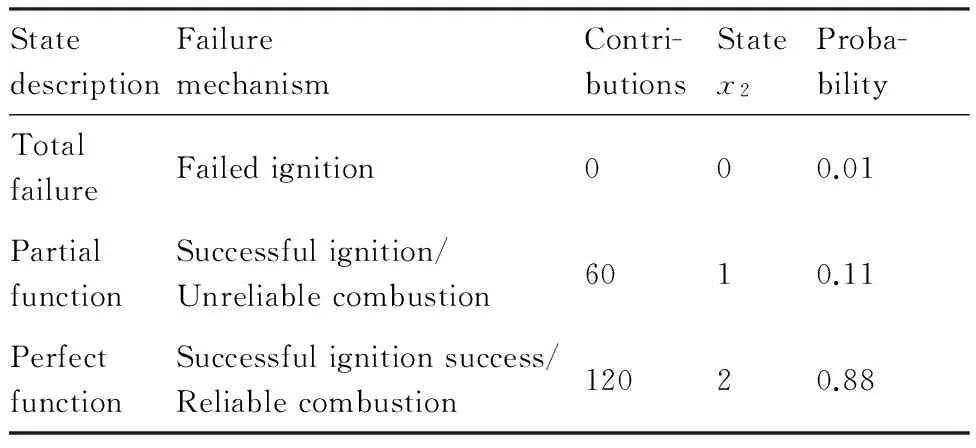
表2 主燃燒單元B1狀態概率Table 2 State probability of main combustor B1

表3 加力燃燒單元B2狀態概率Table 3 State probability of afterburner B2

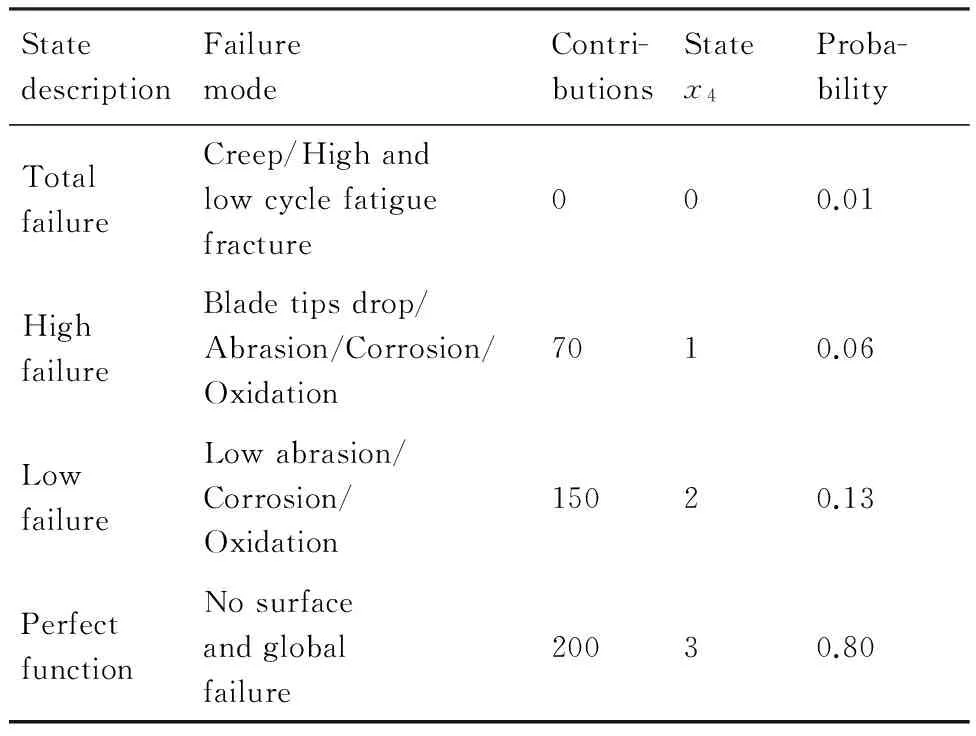
表4 渦輪單元C狀態概率Table 4 State probability of turbine C

根據航空發動機系統結構(如圖1(a)所示)以及工作原理(圖1(b)所示)，整個發動機系統的性能狀態輸出，考慮由圖1(d)中框圖結構形式輸出。考慮整個航空發動機推動力輸出符合下列公式

S=φ(a,b1,b2,c)=min{a,b1+b2,c}

(18)

式中：S為系統推動力輸出量；a為壓氣機單元功能貢獻量；b1為主燃燒室單元B1功能貢獻量；b2為加力燃燒室單元B2功能貢獻量；c為渦輪轉子單元功能貢獻量。貢獻量為整體推力貢獻的單位分量，主要是用來方便確定系統狀態。

4.1 狀態類與邊界點

根據發動機系統結構狀態情況的定量描述，以及式(18)、圖1(d)和表1～表4相關數據。為方便，用(x1x2x3x4)表示系統狀態輸出，則系統狀態等價類的計算結果展示于表5。

表5 系統輸出的狀態等價類Table 5 State equivalence Ω of system output

進一步，不妨將上述9個等價類按照貢獻量輸出情況進行適當合并，簡化為5個等價類。依據等價類定義3，表5中給出了細分9個等價類時的邊界點，顯然從表5可以看出等價類中邊界點個數要比等價類所有等價元素個數少很多，這也說明了邊界點方法可以減少計算量。根據定義4、定義5，以及表5中數據，下面給出上等價類如表6 所示。

根據定義5以及表5、表6中相關數據，下面給出狀態類下邊界點以及上狀態類的下邊界點相關數據，如表7所示。

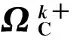
表6 系統輸出的上等價類Table 6 Upper equivalence Ω of system output

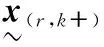
表7 系統輸出的下邊界點Table 7 Lower boundary points of system output

根據以上計算得到的邊界點數據，應用文中給出的分析方法計算多態系統的可靠度。

4.2 MSCS的結構函數運算

應用析取式(6)中的結構函數計算方法，下面給出基于表7中邊界點數據的結構函數表達式。

基于表7中邊界點及式(6)，給出主控邊界下結構函數的框圖形式如圖2所示。

為便于應用，圖2可表示為

(19)

若應用表7中狀態類邊界點，以及式(7)中的L-L方法，則析取形式的結構函數應為

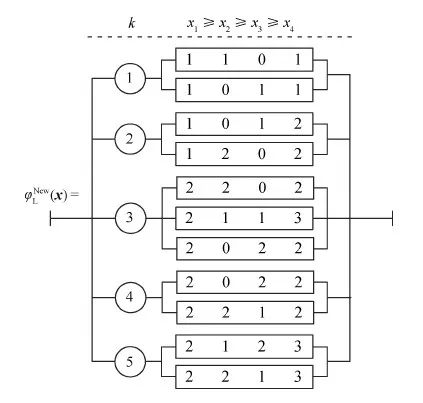
圖2 新方法框圖形式Fig.2 Diagram form of new approach

(20)

為驗證結構函數的有效性，下面給出單元狀態向量[2,2,0,3]時系統所處狀態計算。根據式(19)和式(20)有

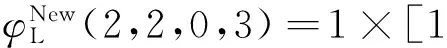
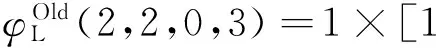
事實上，根據表5中狀態等價類的劃分，單元狀態向量[2,2,0,3]對應的系統狀態為3。這表明基于狀態等價類的主控邊界點能夠完全控制所有其他狀態向量。

4.3 MSCS的可靠性計算

為演示新方法的有效性，考慮新框圖算法和L-L方法，應用邊界點和表7中相關數據，計算各狀態下可靠度。下面僅給出狀態1的可靠度計算過程，其他計算結果參見表8。

基于表7中上等價類的下邊界點數據，應用圖2的框圖結構算法以及式(13)，系統處于狀態1的可靠度應為

表8 系統可靠度計算結果Table 8 Results of system reliability

E[(1101)]+E[(1011)]-E[(1111)]=

(p1,1+p1,2)(p2,1+p2,2)·1·

(p4,1+p4,2+p4,3)+(p1,1+p1,2)·1·

(p3,1+p3,2)(p4,1+p4,2+p4,3)-

(p1,1+p1,2)(p2,1+p2,2)(p3,1+p3,2)·

(p4,1+p4,2+p4,3)=(0.04+0.94)·

(0.11+0.88)(0.06+0.13+0.80)+

(0.04+0.94)(0.08+0.91)·

(0.06+0.13+0.80)-(0.04+0.94)·

(0.11+0.88)(0.08+0.91)·

(0.06+0.13+0.80)=0.970 102 98

若應用表7中一般等價類的邊界點數據及式(14)，L-L方法析取形式下系統處于狀態1的可靠度應為

1-E{[1-(1101)][1-(1011)]·

[1-(1012)][1-(1202)]·

[1-(2202)][1-(2112)]·

[1-(2022)][1-(2212)]·

[1-(2123)][1-(2213)]}=

E[(1101)]+E[(1011)]-

E[(1111)]=0.970 102 98

顯然析取形式下，應用L-L方法的計算工作量較大，而本文提出的方法較為簡潔，減少計算復雜度。為便于分析比較，將上述計算結果列于表8。

從表8中數據知，提出的新方法與L-L方法計算結果均為一致。上述計算結果也表明，若整個發動機系統處于狀態 4，即次完美狀態，則壓氣機的工作狀態必為完美狀態，而渦輪至少處于低度磨損與腐蝕、輕度高溫氧化狀態，而主力和助力燃燒室至少一個子單元處于完美狀態。

根據表8中計算結果，系統處于某個特定狀態k的概率應為

Pr{φ(x)=0}=R0-R1=1-0.970 1=0.029 9

Pr{φ(x)=1}=R1-R2=0.970 1-0.910 3=

0.059 8

Pr{φ(x)=2}=R2-R3=0.910 3-0.872 5=

0.037 8

Pr{φ(x)=3}=R3-R4=0.872 5-0.857 1=

0.015 4

Pr{φ(x)=4}=R4-R5=0.857 1-0.730 4=

0.126 7

Pr{φ(x)=5}=R5=0.730 4

從而系統狀態的期望性能水平為

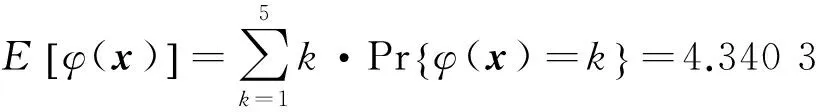
即系統可靠性性能平均狀態水平為4.340 3。

進一步，根據式(17)，不妨取c=100,β=0.5，基于顧客角度，該航空發動機系統的負效用水平應為

Pr{φ(x)=5-k}}=95.68

系統完全失效時的最大負效用為200.593 9，表明系統性能需要改進。

5 結 論

1) 鑒于工程復雜系統處于多個狀態運行的現實問題，將多元離散函數理論引入結構函數描述系統狀態，給出了單調關聯系統的數學概念，狀態等價類，控制等價類的主導向量等相關定義與邏輯方法。

2) 基于離散函數理論的析取與合取運算的代數規則，將二元邏輯運算推廣到多元邏輯運算，給出了多狀態系統的析取與合取范式，推導了系統多狀態邊界點的結構函數。為便于運算，提出了集合運算的德摩根律方法，簡化了邊界點下系統的結構函數和可靠度表達式。為評估整個系統所處的平均性能，給出了系統的期望狀態計算式，考慮系統面向顧客的偏好與需求，建立了基于負效用函數的性能效用模型。

3) 為驗證模型的有效性與合理性，將一個某型航空發動機系統進行框圖分解，基于各個子單元對系統的貢獻度，給出了系統等價類，獲取了系統狀態相關的上下邊界點數據。為便于運算，算例中構建了新型的框圖式算法，給出了析取與合取形式下的結構函數表示，大大減少了計算復雜度，增加了問題描述的清晰度。通過新框圖算法和德摩根律方法，降低了可靠度的計算復雜程度。

4) 通過算例分析，基于本文提出的狀態等價類的主控邊界點數據，以L-L方法作為比較對象，提出的方法能夠尋找到完全控制等價類中其它向量，而且計算量簡潔許多，并不需要計算所有滿足≥0狀態的所有邊界點，只需要計算控制其他邊界點的狀態等價類中主控邊界點即可，大大減少計算復雜度。

5) 本文給出的狀態等價類的主控邊界點方法，推廣了L-L方法，通過實例驗證了提出方法的有效性與合理性。然而隨著單元數和子單元狀態數的增加，復雜度也快速增加，可以進一步考慮使用計算機，給出系統狀態和可靠度的計算程序以便于應用。

[1] CHAHKANDI M, RUGGERI F, SUAREZ L A. A generalized signature of repairable coherent systems[J]. IEEE Transactions on Reliability, 2016, 65(1): 434-445.

[2] BARLOW R E, WU A S. Coherent systems with multi-state components[J]. Mathematics of Operations Research, 1978, 3(4): 275-281.

[3] EI-NEWEIHI E. Multistate coherent systems[J]. Journal of Applied Probability, 1978, 15(4): 675-688.

[4] NATRING B. Two suggestions of how to define a multistate coherent system[J]. Advances in Applied Probability, 1982, 14(2): 434-455.

[5] HUANG H Z, TONG X, ZUO M J. Posbist fault tree analysis of coherent systems[J]. Reliability Engineering & System Safety, 2004, 84(2): 141-148.

[6] AVEN T. On performance measures for multistate monotone systems[J]. Reliability Engineering & System Safety, 1993, 41(3): 259-266.

[7] BOEDIGHEIMER R A, KAPUR K C. Customer-driven reliability models for multistate coherent systems[J]. IEEE Transactions on Reliability, 1994, 43(1): 46-50.

[8] LUO T, TRIVEDI K S. An improved algorithm for coherent system reliability[J]. IEEE Transactions on Reliability, 1998, 47(1): 73-78.

[9] BOUTSIKAS M V, KOUTRAS M V. Generalized reliability bounds for coherent structures[J]. Journal of Applied Probability, 2000, 37(3): 778-794.

[10] ESARY J D, PROSCHAN F. A reliability bound for systems of maintained, interdependent components[J]. Journal of the American Statistical Association, 1970, 65(329): 329-338.

[11] HSIEH Y C. New reliability bounds for coherent systems[J]. Journal of the Operational Research Society, 2003, 54(9): 995-1001.

[12] LI J A, WU Y, LAI K K, et al. Reliability estimation of multi-state components and coherent systems[J]. Reliability Engineering & System Safety, 2005, 88(1): 93-98.

[13] XUE J, YANG K. Dynamic reliability analysis of coherent multistate systems[J]. IEEE Transactions on Reliability, 1995, 44(4): 683-688.

[14] CUI L, LI H. Analytical method for reliability and MTTF assessment of coherent systems with dependent components[J]. Reliability Engineering & System Safety, 2007, 92(3): 300-307.

[15] LIU Y W, KAPUR K C. Reliability measures for dynamic multistate nonrepairable systems and their applications to system performance evaluation[J]. IIE Transactions, 2006, 38(6): 511-520.

[16] NATVIG B. On the deterioration of non-repairable multistate strongly coherent systems[J]. Journal of Applied Probability, 2014, 51(51): 69-81.

[17] KUNDU P, HAZRA N K, NANDA A K. Reliability study of a coherent system with single general standby component[J]. Statistics & Probability Letters, 2016, 110: 25-33.

[18] ERYILMAZ S. A new look at dynamic behavior of binary coherent system from a state-level perspective[J]. Annals of Operations Research, 2014, 212(1): 115-125.

[19] ZHANG X, WILSON A. System reliability and component importance under dependence: A Copula approach[J]. Technometrics, 2016: 1-28.

[20] POLPO A, SINHA D, DE B. Nonparametric Bayesian estimation of reliabilities in a class of coherent systems[J]. IEEE Transactions on Reliability, 2013, 62(2): 455-465.

[21] KUNDU P, HAZRA N K, NANDA A K. Reliability study of a coherent system with single general standby component[J]. Statistics & Probability Letters, 2016, 110: 25-33.

[22] FRANKO C, OZHKUT M, KAN C. Reliability of coherent systems with a single cold standby component[J]. Journal of Computational & Applied Mathematics, 2015, 281(C): 230-238.

[23] GRIFFITH W S. Multistate reliability models[J]. Journal of Applied Probability, 1980, 17(3): 735-744.

[24] BUTLER D A. Bounding the reliability of multi-state systems[J]. Operations Research, 1982, 30(3): 530-544.

[25] BLOCK H W, SAVITS T H. A decomposition for multistate monotone systems[J]. Journal of Applied Probability, 1982, 19(2): 391-402.

[26] HUDSON J C, KAPUR K C. Reliability bounds for multi-state systems with multistate components[J]. Operations Research, 1985, 33(1): 153-160.

[27] LISNIANSKI A, LEVITIN G. Multi-state system reliability assessment, optimization, application[M]. Singapore: World Scientific, 2003: 89-153.

[28] LIU Y W, KAPUR K C. Customer’s cumulative experience measures for reliability of non-repairable aging multistate systems[J]. Quality Technology and Quantitative Management, 2007, 4(2): 225-234.

[29] MAGANA S, ALBERTO C. Dynamic reliability based performance measures for multi-state systems[D]. Seattle, WA: University of Washington, 2010: 116-130.

[30] LIU Y W. Multi-state system reliability: Models, dynamic measures and applications[D]. Seattle, WA: Univesity of Washington, 2006: 115-121.

[31] XUE J, YANG K. Dynamic reliability analysis of coherent multistate systems[J]. IEEE Transactions on Reliability, 1995, 44(4): 683-688.

[32] 劉長富, 鄧明. 航空發動機結構分析[M]. 西安: 西北工業大學出版社, 2006: 72-112.

LIU C F, DENG M. Structural analysis of aeroengine[M]. Xi’an: Northwestern Polytechnical University Press, 2006: 72-112 (in Chinese).

(責任編輯： 張晗)

*Correspondingauthor.E-mail:sunyc@nuaa.edu.cn

Reliabilityanalysisformulti-statecoherentsystemwithmonotoniccomponentsbasedonpivotalboundarypointsofclusteringstates

ZHANGYongjin1，SUNYouchao2,*，ZHANGYanjun3

1.SchoolofMathematicsandPhysics,AnhuiUniversityofTechnology,Maanshan243002,China2.CollegeofCivilAviation,NanjingUniversityofAeronauticsandAstronautics,Nanjing211106,China3.CollegeofMechanicalEngineering,YangzhouUniversity,Yangzhou225127,China

Consideringthemonotoneandcoherenceofthemulti-statesystem,themultiplediscretefunctiontheoryisintroducedtodescribethestructurefunctionofsystemstate.Thelogicapproachesfortheequivalenceclassofthecomponentstatewhichcontrolthestatevectorofsystemareproposed,andtheexpressionsforthestatestructurefunction,reliabilityandexpectedstatesarederivedforthemulti-statecoherentsystem.Toavoidthecomplexityofcomputationcausedbythenumberofthestate,theDemogenlawandthenewblockdiagramalgorithmaredevelopedtosimplifytheexpressionforthesystemreliability.Anillustrativeexampleofacertaintypeofaeroengineverifiestheeffectivenessofthelogicvectormeasurecontrollingthestateequivalenceclassandtheblockdiagramalgorithm.Itprovidestheoreticalbasisforreliabilitydesignandreliabilitymanagementofsystemengineering.

pivotalboundarypoint;discretefunction;multi-statecoherentsystem;monotonicity;reliability

2016-10-19;Revised2017-02-26;Accepted2017-04-05;Publishedonline2017-04-191331

URL：www.cnki.net/kcms/detail/11.1929.V.20170419.1331.008.html

s：NationalNaturalScienceFoundationofChina(U1333119,60979019,60572171,51605424,71601002);CAACScienceandTechnologyProject(MHRD201123,MHRD200908,MHRD0722);NaturalScienceFoundationofJiangsuProvince(BK20150455).

2016-10-19；退修日期2017-02-26；錄用日期2017-04-05； < class="emphasis_bold">網絡出版時間

時間：2017-04-191331

www.cnki.net/kcms/detail/11.1929.V.20170419.1331.008.html

國家自然科學基金 (U1333119,60979019,60572171,51605424,71601002)； 中國民航局科技基金 (MHRD201123,MHRD200908,MHRD0722)； 江蘇省自然科學基金 (BK20150455)

.E-mailsunyc@nuaa.edu.cn

張永進， 孫有朝， 張燕軍． 基于聚類狀態主控邊界點的單調多態關聯系統可靠性分析J． 航空學報,2017,38(8):220868.ZHANGYJ,SUNYC,ZHANGYJ.Reliabilityanalysisformulti-statecoherentsystemwithmonotoniccomponentsbasedonpivotalboundarypointsofclusteringstatesJ.ActaAeronauticaetAstronauticaSinica,2017,38(8):220868.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2017.220868

V231; TB114.3； TH112

A

1000-6893(2017)08-220868-12