近場試驗條件對二維干涉儀測向系統(tǒng)的影響

李 琳，居 易

(中國船舶重工集團公司第七二三研究所，江蘇 揚州 225001)

近場試驗條件對二維干涉儀測向系統(tǒng)的影響

李 琳，居 易

(中國船舶重工集團公司第七二三研究所，江蘇 揚州 225001)

基于干涉儀測向原理，分析了干涉儀測向系統(tǒng)近場試驗驗證時產(chǎn)生較大誤差的2種原因，仿真給出了2種條件下二維干涉儀的測向結(jié)果受輻射源距離以及轉(zhuǎn)臺旋轉(zhuǎn)角度的影響，推導(dǎo)出天線位置偏心時的測向誤差校正公式，提出用仿真結(jié)果對試驗中由于球面?zhèn)鞑ギa(chǎn)生的測角誤差進(jìn)行補償?shù)姆椒ā?/p>

干涉儀測向；誤差；偏心；球面?zhèn)鞑?/p>

0 引 言

干涉儀測向技術(shù)自出現(xiàn)以來就以其測向精度高、實時性好、成本低等優(yōu)點被廣泛應(yīng)用于電子偵察領(lǐng)域。干涉儀測向的實質(zhì)是利用無線電波在測向基線上形成的相位差來確定來波方向[1]。而二維干涉儀可同時對來波的方位角和俯仰角進(jìn)行測向。

干涉儀測向系統(tǒng)使用前需通過試驗驗證和通道間相位差標(biāo)校，在測試試驗過程中，如果忽略試驗條件近場特性而使相位標(biāo)校引入較大誤差，將嚴(yán)重影響測向系統(tǒng)應(yīng)用時測向的正確性。

1 二維單基線測向原理

如圖1所示的三元陣，陣元0，1的連接線與陣元0，2的連接線垂直，建立圖1所示的坐標(biāo)系。其中，θv為來波的俯仰角，θh為來波的方位角，d為單基線長度。

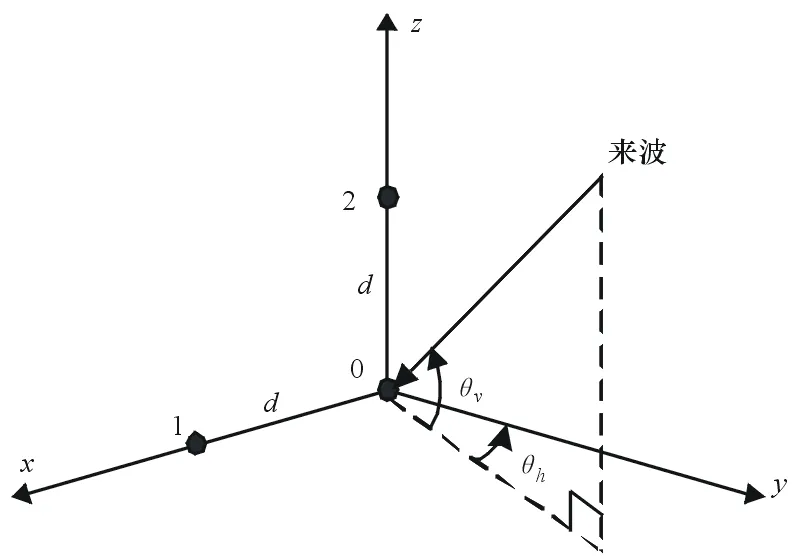
圖1 二維單基線原理說明圖

俯仰角和方位角的計算公式如下：

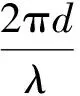
(1)

(2)

式中：φx為0，1基線相位差；φz為0，2基線相位差。

二維多基線干涉儀測向是利用多基線解模糊得到單基線相位差后經(jīng)過式(1)、式(2)計算得到測向結(jié)果，多基線解模糊算法比較復(fù)雜，本文不再贅述。

2 近場試驗條件下測向誤差原因分析

2.1 天線陣安裝位置偏心

測向系統(tǒng)試驗時，是將接收天線陣安裝在二維測試轉(zhuǎn)臺上，使用固定模擬目標(biāo)向天線陣發(fā)射信號，以驗證測向的準(zhǔn)確性[2]。很多情況下，由于天線結(jié)構(gòu)和測試轉(zhuǎn)臺結(jié)構(gòu)的限制，天線陣安裝位置會偏離二維測試轉(zhuǎn)臺的中心，使得同一目標(biāo)對于二者有不同的方向，此時用測試轉(zhuǎn)臺旋轉(zhuǎn)角度來衡量干涉儀測向結(jié)果會出現(xiàn)一定的誤差。

下面以某二維L型天線陣為例，討論天線安裝位置偏心時，測向結(jié)果的誤差。該L型天線陣在轉(zhuǎn)臺上的安裝位置如圖2所示，水平天線陣與轉(zhuǎn)臺的俯仰轉(zhuǎn)軸平行。天線陣安裝在與轉(zhuǎn)臺相交的斜面上。其中，以轉(zhuǎn)臺俯仰轉(zhuǎn)軸為x軸，水平轉(zhuǎn)軸為z軸，轉(zhuǎn)臺中心為原點O建立Oxyz坐標(biāo)系，Otxtytzt坐標(biāo)系是將Oxyz坐標(biāo)系的原點O平移到L型天線陣頂點Ot得到的，那么可以在此基礎(chǔ)上計算目標(biāo)在兩坐標(biāo)系下的俯仰角和方位角的誤差。

圖2 偏心示意圖

可以將測試時二維轉(zhuǎn)臺的旋轉(zhuǎn)看作坐標(biāo)系Oxyz的旋轉(zhuǎn)。假設(shè)有一固定輻射源A，在Oxyz坐標(biāo)系中坐標(biāo)為(x,y,z)，試驗時轉(zhuǎn)臺先繞x軸順時針旋轉(zhuǎn)角度α(垂直旋轉(zhuǎn)角度)，再繞z軸旋轉(zhuǎn)γ(水平旋轉(zhuǎn)角度)，然后平移向量t，得到Otxtytzt坐標(biāo)系，如圖3所示。

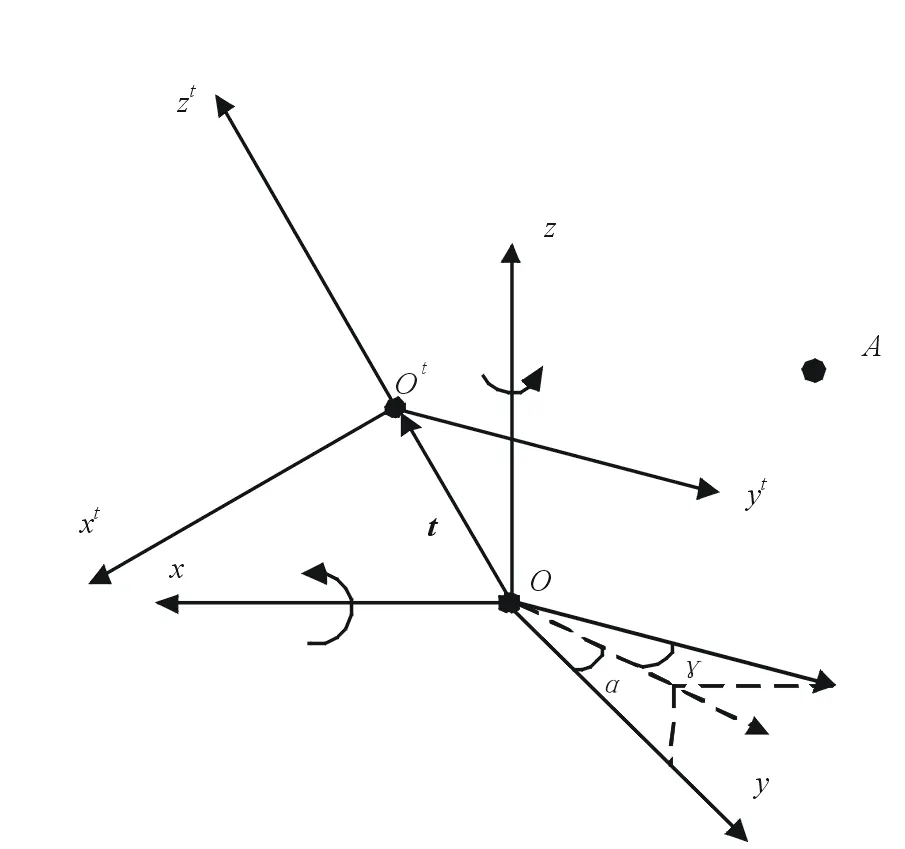
圖3 坐標(biāo)系轉(zhuǎn)換示意圖

那么，固定位置輻射源在Otxtytzt坐標(biāo)系中的坐標(biāo)(xt,yt,zt)為：

(3)

(4)

(5)

式中：Aα，Aγ分別為繞x軸旋轉(zhuǎn)角度α，繞z軸旋轉(zhuǎn)角度γ的坐標(biāo)系旋轉(zhuǎn)矩陣；t為轉(zhuǎn)臺中心到L型天線陣頂點的向量OOt。

輻射源在兩坐標(biāo)系中的俯仰角和方位角為：

θh=arctan(x/y)

(6)

θv=arcsin(z/sqrt(x2+y2+z2))

(7)

(8)

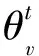
(9)

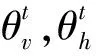
以轉(zhuǎn)臺坐標(biāo)系的測向結(jié)果作基準(zhǔn)，俯仰角和方位角的誤差可以表示為：

(10)

(11)

對圖2所示的天線陣偏心所產(chǎn)生的測向誤差進(jìn)行仿真分析。假設(shè)相對于Oxyz坐標(biāo)系，L型天線陣頂點坐標(biāo)為(0.2,0.6,1.2)m，固定輻射源的初始坐標(biāo)為(0.2,0.6,ly)m。選擇ly=50,α,γ從-60°變化到60°，變化間隔為1°，仿真得到的測角誤差如圖4、圖5所示。

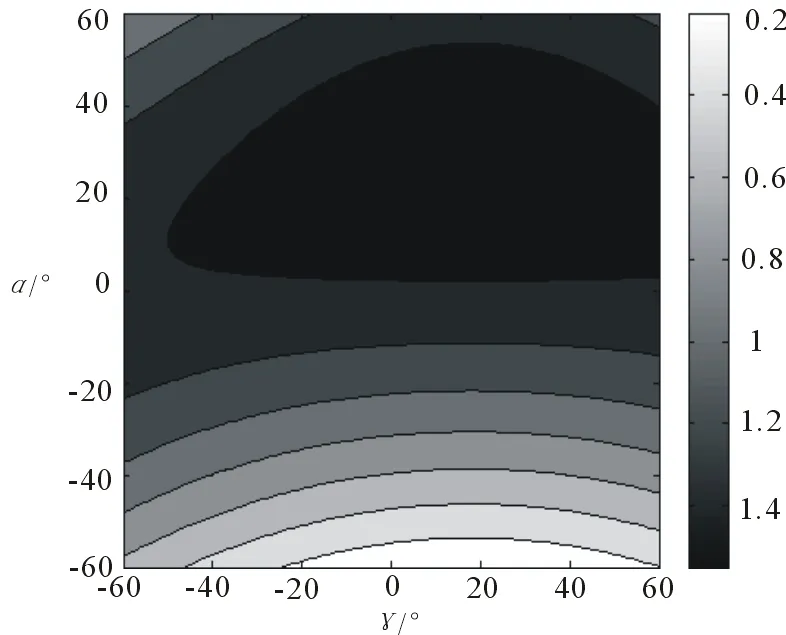
圖4 俯仰角誤差

圖5 方位角誤差

觀察俯仰角和方位角測角誤差隨轉(zhuǎn)臺的垂直旋轉(zhuǎn)角度和水平旋轉(zhuǎn)角度的變化，可以看出|e|最大值接近1.5°。圖中分層規(guī)律顯示，垂直旋轉(zhuǎn)角度主要影響俯仰角，水平旋轉(zhuǎn)角度主要影響方位角。

選擇α=18°，γ=-55°，ly從10 m增加到100 m，俯仰角和方位角的誤差如圖6所示。俯仰角和方位角的誤差隨輻射源的距離增大而減小。并且在一定范圍內(nèi)，距離減小，誤差急劇增大。距離為10 m時，俯仰角誤差甚至達(dá)到7°。

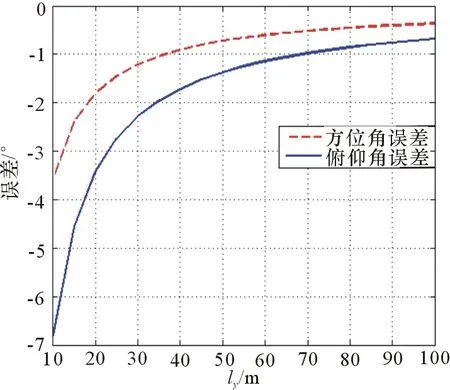
圖6 輻射源距離對俯仰角和方位角的影響

綜上分析，由于天線安裝位置的偏心，使得測向系統(tǒng)的測向結(jié)果與轉(zhuǎn)臺坐標(biāo)系的定向結(jié)果之間存在誤差。

綜合圖4、圖5、圖6，該誤差在輻射源距離50 m時還能達(dá)到接近1.5°，輻射源距離越近，誤差越大。可見在內(nèi)場試驗時，偏心對測向結(jié)果有相當(dāng)大的影響，如果不對偏心的影響進(jìn)行分析和校正，簡單地以轉(zhuǎn)臺旋轉(zhuǎn)角度衡量測向結(jié)果，會嚴(yán)重影響對測向系統(tǒng)的試驗驗證。

2.2 近場電磁波球面?zhèn)鞑サ挠绊?/p>

由輻射源發(fā)出的電波是球面波，到接收天線的距離很大(與波長相比)時，可以近似認(rèn)為平面波[3]，干涉儀測向系統(tǒng)是在這一理論基礎(chǔ)上建立的。但試驗場受空間限制，輻射源距離一般不滿足近似平面波條件。

以一維單基線兩陣元為例，說明電磁波的球面?zhèn)鞑ツＪ较玛囋g相位差與近似平面波傳播時相位差的計算方式不同，如圖7所示，O為輻射源，A、B為接收陣元。

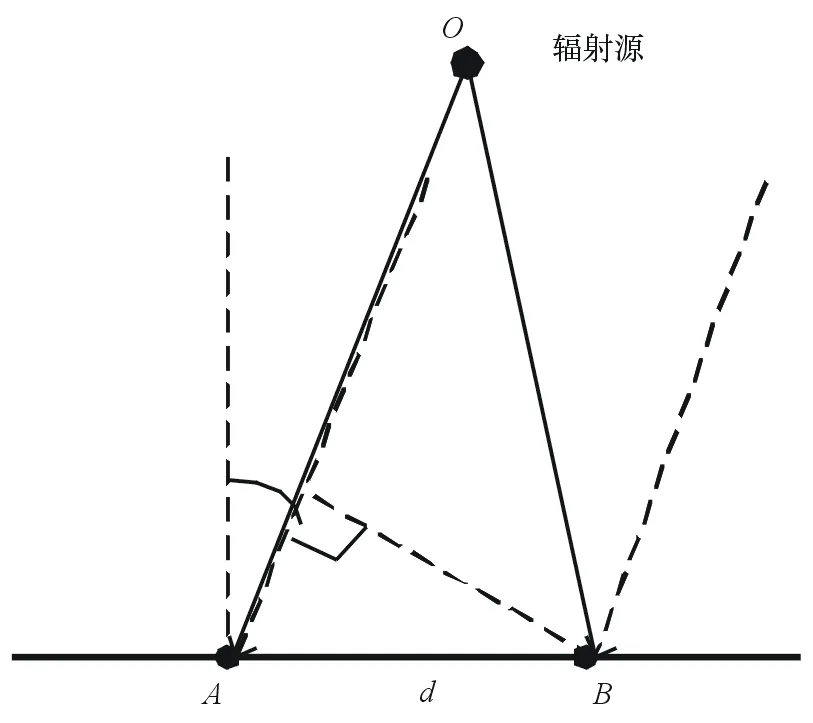
圖7 一維單基線測向說明圖

輻射源距離遠(yuǎn)大于陣元間距d時，電磁波近似為平面波傳播，A，B接收到的信號波達(dá)角近似相同(如圖7虛線所示)，波達(dá)角為θ，波程差為dsinθ，相位差φ為：

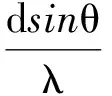
(12)

而球面波傳播時，波程差為OA-OB(如圖7實線所示)，相位差φ為：

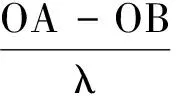
(13)

干涉儀測向系統(tǒng)是在式(12)的基礎(chǔ)上計算波達(dá)角的。但是近場試驗時，實際相位差的理論值為式(13)的結(jié)果，最終造成測向誤差。

仍以圖2所示的天線陣為例，采用適當(dāng)?shù)幕€比可得到各接收陣元的坐標(biāo)，通過式(13)計算出陣元間相位差，經(jīng)過適當(dāng)?shù)慕饽：惴ǎ瑥亩M出干涉儀測向系統(tǒng)的測角結(jié)果，與通過坐標(biāo)計算得到的方位角和俯仰角的精確結(jié)果進(jìn)行對比分析。因為考慮的是測向系統(tǒng)本身的測向誤差，所以僅在Otxtytzt坐標(biāo)系下分析。俯仰角和方位角的測角誤差為：

(14)

(15)

式中：θhc,θvc為干涉儀測向系統(tǒng)得到的方位角和俯仰角。

固定輻射源的初始坐標(biāo)為(0,0,ly)。ly分別選20，35，50,α,γ從-60°變化到60°，變化間隔為1°。仿真的結(jié)果如圖8、圖9所示。

圖8 俯仰角測角誤差

圖9 方位角測角誤差

從圖中可以看出，輻射源的距離和轉(zhuǎn)臺的旋轉(zhuǎn)角度，都對測角誤差有影響。方位角測角誤差受距離影響較大，而俯仰角誤差也受距離影響，兩者都隨著距離的增大而減小。

為了進(jìn)一步分析這3個因素的影響，以方位角誤差為例，轉(zhuǎn)臺旋轉(zhuǎn)角度選取(45°,45°)和(60°,60°)，得到圖10。

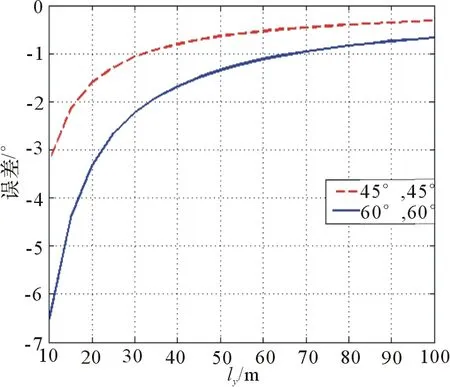
圖10 球面?zhèn)鞑ゾ嚯x的影響

圖10顯示，距離對測角結(jié)果影響很大。(45°,45°)的情況，距離近時，誤差可以達(dá)到3°；距離增大到60 m，誤差才減小到0.5°以內(nèi)。由圖9也可以看出，仿真選取的轉(zhuǎn)臺旋轉(zhuǎn)角度(45°,45°)并不是最惡劣的情況，若是旋轉(zhuǎn)角度選取更惡劣的情況，會造成同一距離產(chǎn)生的誤差相對增大，如圖10中實線所示。

旋轉(zhuǎn)角度選擇(45°,45°)，相位噪聲服從均值為0、方差為0.05×2π的正態(tài)分布，采樣間隔為1 s，觀測10 s，仿真得到方位角誤差，并用圖10中的結(jié)果對其進(jìn)行校正，結(jié)果如圖11所示。

在電磁波實際以球面?zhèn)鞑r，不論是距離還是轉(zhuǎn)臺旋轉(zhuǎn)角度，都對測向結(jié)果產(chǎn)生較大的誤差，這種影響是不能忽略的，如果沒有考慮到近場球面?zhèn)鞑r的這類誤差，也會對測向系統(tǒng)的試驗驗證造成嚴(yán)重影響。

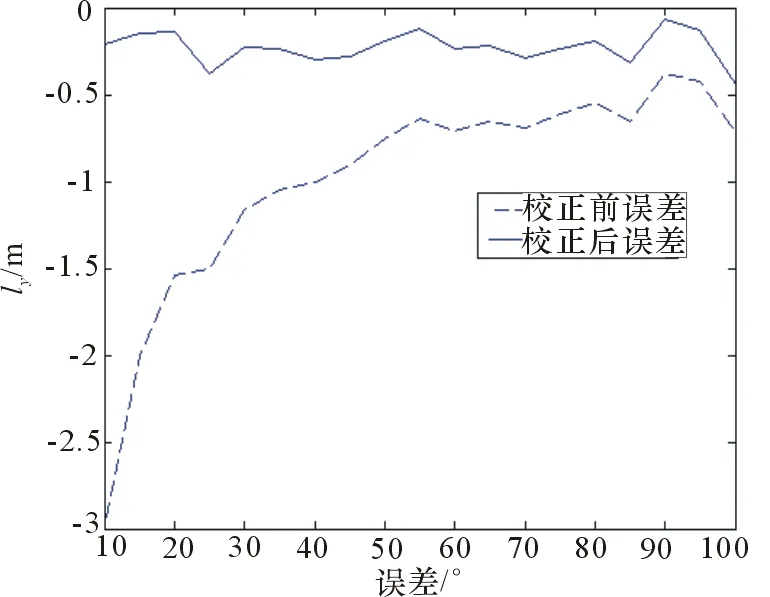
圖11 方位角誤差校正結(jié)果

3 結(jié)束語

干涉儀測向系統(tǒng)產(chǎn)生誤差的原因有很多[4]，本文僅分析了由于試驗時的近場條件，二維干涉儀測向系統(tǒng)產(chǎn)生測向誤差的相關(guān)因素，仿真了產(chǎn)生的測角誤差，得出以下結(jié)論：

(1) 天線安裝位置偏心會使干涉儀測向結(jié)果與轉(zhuǎn)臺旋轉(zhuǎn)結(jié)果產(chǎn)生較大偏差，在試驗時可利用式(10)、式(11)進(jìn)行校正。

(2) 試驗不滿足遠(yuǎn)場條件，會使干涉儀測向系統(tǒng)本身的測角結(jié)果產(chǎn)生很大誤差，可盡可能地增大輻射源的距離、減小轉(zhuǎn)臺旋轉(zhuǎn)范圍來減小誤差。

(3) 受試驗場空間限制，輻射源距離無法增大時，可以對不同距離、不同轉(zhuǎn)臺旋轉(zhuǎn)角度的測角誤差進(jìn)行仿真計算，形成完備的測角誤差數(shù)據(jù)庫，對干涉儀測向結(jié)果進(jìn)行校正，此方法有待于進(jìn)一步仿真驗證。

[1] 肖秀麗.干涉儀測向原理[J].中國無線電,2006(5):43-49.

[2] 王晨晨,房景仕.二維測試轉(zhuǎn)臺偏心誤差修正技術(shù)研究[J].自動化與信息工程,2013,34(4):11-15.

[3] 薛建彬.現(xiàn)代通信技術(shù)[M].北京:北京理工大學(xué)出版社,2013.

[4] 張娟,劉恒,何冠良.干涉儀測向系統(tǒng)相位誤差校準(zhǔn)方法[J].雷達(dá)與對抗,2014,34(3):23-26.

InfluenceofNear-fieldTestConditionsonTwo-dimensionalInterferometerDirection-findingSystem

LI Lin,JU Yi

(The 723 Institute of CSIC,Yangzhou 225001,China)

Based on the principle of interferometer direction-finding,this paper analyzes two reasons of measurement error when the interferometer direction-finding system is in near-field test,simulates the impact of emitter distance and rotation angle of the turntable on 2D interferometer direction-finding results under the two conditions,educes the direction-finding error correction formula when the antenna position is off-center,proposes the method using the simulation result to compensate the angle measurement error caused by the spherical propagation in tests.

interferometer direction-finding;error;off-center;spherical propagation

TN971

A

CN32-1413(2017)05-0044-04

10.16426/j.cnki.jcdzdk.2017.05.009

2017-09-06