Constrained adaptive neural network control of an MIMO aeroelastic system with input nonlinearities

Gou Yiyong,Li Hongbo,Dong Xinmin,Liu Zongcheng

Aeronautics and Astronautics Engineering College,Air Force Engineering University,Xi’an 710038,China

Constrained adaptive neural network control of an MIMO aeroelastic system with input nonlinearities

Gou Yiyong,Li Hongbo,Dong Xinmin*,Liu Zongcheng

Aeronautics and Astronautics Engineering College,Air Force Engineering University,Xi’an 710038,China

Aeroelastic system;Constrained control;Flutter suppression;Input nonlinearities;RBFNNs

A constrained adaptive neural network control scheme is proposed for a multi-input and multi-output(MIMO)aeroelastic system in the presence of wind gust,system uncertainties,and input nonlinearities consisting of input saturation and dead-zone.In regard to the input nonlinearities,the right inverse function block of the dead-zone is added before the input nonlinearities,which simplifies the input nonlinearities into an equivalent input saturation.To deal with the equivalent input saturation,an auxiliary error system is designed to compensate for the impact of the input saturation.Meanwhile,uncertainties in pitch stiffness,plunge stiffness,and pitch damping are all considered,and radial basis function neural networks(RBFNNs)are applied to approximate the system uncertainties.In combination with the designed auxiliary error system and the backstepping control technique,a constrained adaptive neural network controller is designed,and it is proven that all the signals in the closed-loop system are semi-globally uniformly bounded via the Lyapunov stability analysis method.Finally,extensive digital simulation results demonstrate the effectiveness of the proposed control scheme towards flutter suppression in spite of the integrated effects of wind gust,system uncertainties,and input nonlinearities.

1.Introduction

In the past,aeroelasticity has attracted increasing concern in aircraft design.Aeroelastic systems exhibit a variety of unstable phenomena as a result of the mutual interaction of structural,inertia and aerodynamic forces.1Divergence,flutter,and limit-cycle oscillation are typical unstable phenomena which can degrade an aircraft’s flight performance,and even cause flight mission failure.1,2Thus,a reliable and effective control strategy becomes one of the key issues in aeroelastic system control design.In previous studies,researchers have analyzed the nonlinear responses of aeroelastic systems,and various control schemes have been extensively studied.Based on the l method,Lind and Brenner3have analyzed the unstable responses of aeroelastic systems and studied robust stability margins.To study different aeroelastic phenomena,the NASA Langley Research Center has developed a benchmark active control technology(BACT)wind-tunnel model.4For this BACT wind-tunnel model,several control laws for fluttersuppression have been developed.4–6Considering nonlinear structural stiffness,a model equipped with a single trailingedge(TE)control surface has been developed at Texas A&M University.7Based on this model,a wide variety of control schemes have been designed.8–11Inspired by the limited effectiveness of a single TE control surface,a wing section equipped with a leading-edge(LE)control surface and a TE control surface has been designed,and a large number of control schemes has been proposed.12–16For this wing section with uncertainties,adaptive control has been widely used to suppress flutter.13–15Neural network control and adaptive control have been developed in this filed and compared in control performance.13With respect to external disturbance and uncertainties,Wang et al.14designed an output feedback adaptive controller coupled with an SDU decomposition which avoids the singularity problem arising from estimation of the input matrix.Accounting on the input saturation problem,Lee and Singh15used an auxiliary dynamic system to compensate for the input saturation and proposed a novel control scheme.In addition,a sliding mode control method was also applied to flutter suppression,and Lee and Singh16have designed a higher-order sliding mode controller which accomplished the finite-time flutter suppression of the aeroelastic system.

It is well known that input nonlinearities exist in a real control system,and an aeroelastic control system is no exception.Both input dead-zone and saturation are considered for the uncertain aeroelastic system in this paper.Input saturation and dead-zone may induce deterioration of the aeroelastic control system performance,and even make the aeroelastic control system fail.Consequently,input saturation and deadzone have attracted much attention.Input dead-zone could induce a zero input against a range of set values.17An adaptive dead-zone inverse approach was proposed to tackle a system with input dead-zone.18An adaptive fuzzy output feedback control law,which treats dead-zone inputs as system uncertainties,has been developed.19For the input saturation problem,Chen et al.20designed an auxiliary system,whose input was the error between the saturation input and the desired control input,to compensate for the impact of the input saturation.Li et al.21proposed an adaptive fuzzy output feedback control for output constrained nonlinear systems.In general,some researchers have also studied in integrating input deadzone with saturation.For uncertain multi-input and multioutput(MIMO)nonlinear systems with input nonlinearities,a robust adaptive neural network control was developed.17Yang and Chen22regarded input dead-zone and saturation nonlinearities as a new input saturation problem through a dead-zone inverse approach,and proposed an adaptive neural prescribed performance control law for near-space vehicles.

Motivated by the above discussion,a constrained adaptive neural network control scheme is proposed for an MIMO aeroelastic system with wind gust,system uncertainties,and input nonlinearities.Different from the previous references,it is especially noted that uncertainties in pitch stiffness,plunge stiffness,and pitch damping are all considered.Inspired by Ref.22,the right inverse function block of the dead-zone is added before the input nonlinearities,by which the input nonlinearities can be regarded as a new input saturation.22To handle the new input saturation,an auxiliary error system is designed to compensate for the impact of the input saturation.Radial basis function neural networks(RBFNNs)are also applied to approximate the system uncertainties.A novel constrained adaptive control law is developed by using the backstepping control technique.The simulation results of the MIMO aeroelastic control system are presented to verify that the proposed control scheme can accomplish flutter suppression despite the effects of wind gust,system uncertainties,and input nonlinearities.

2.Nonlinear aeroelastic model and preliminary

2.1.Nonlinear aeroelastic model

A two-degree-of-freedom(2-DOF)wing section equipped with LE and TE control surfaces is presented in Fig.1.15The second-order differential equations signifying the dynamic of this aeroelastic system are given by13,14

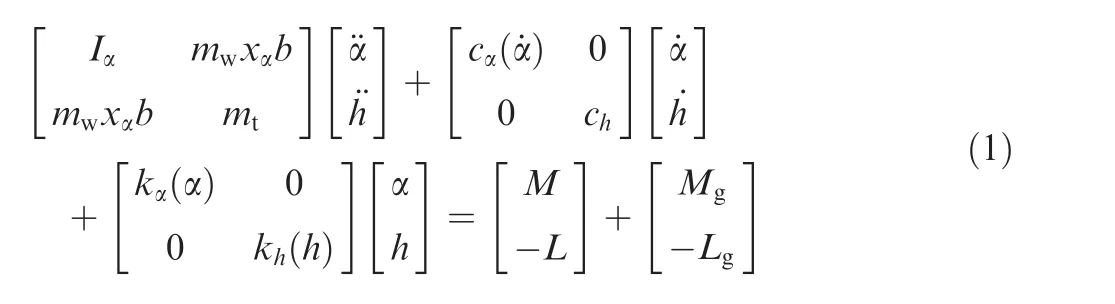
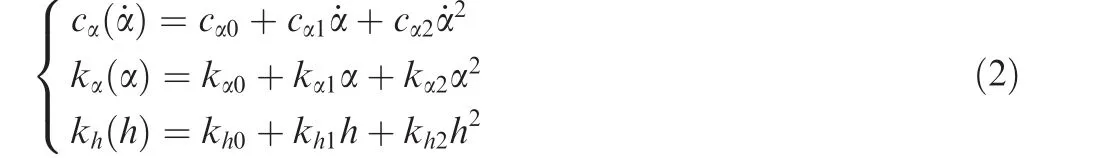
In Eq.(1),MandLrepresent the aerodynamic moment and lift in a quasi-steady form expressed by13

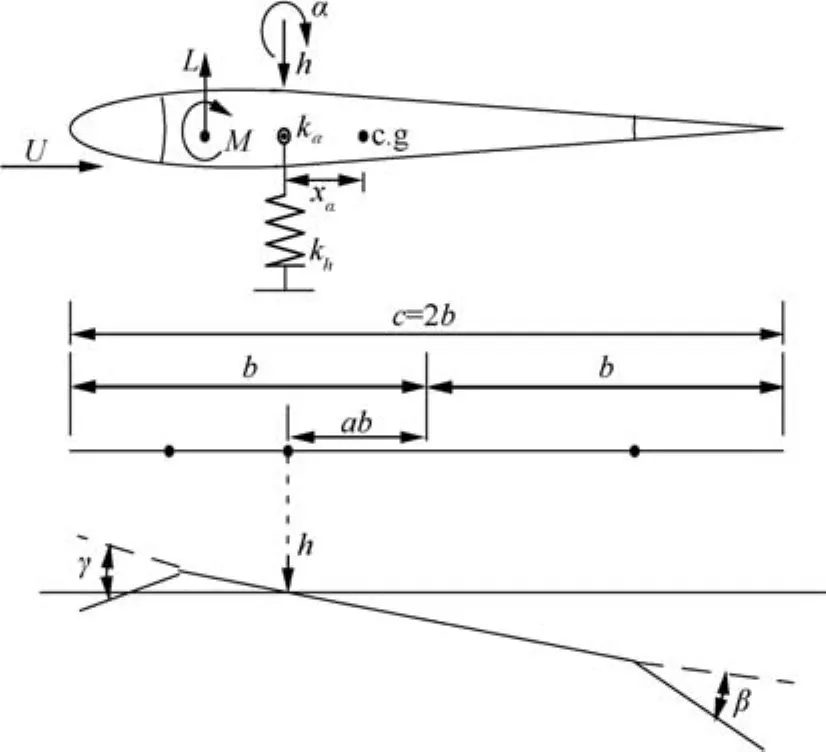
Fig.1 Aeroelastic system with LE and TE control surfaces.15

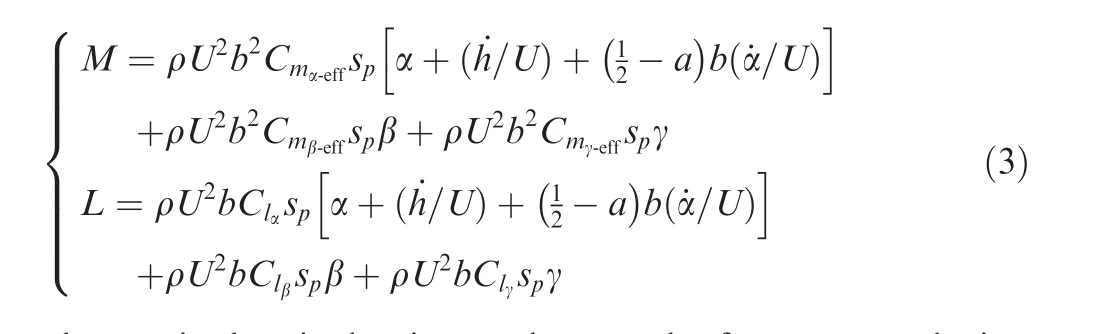
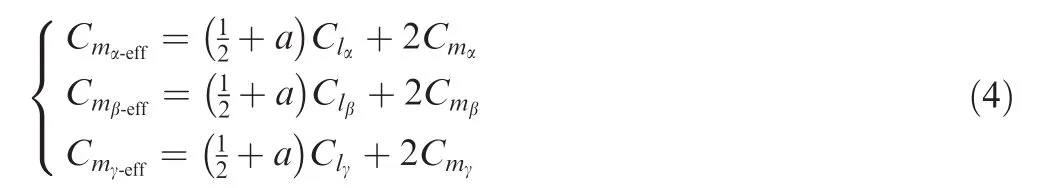
whereCma,CmbandCmcare the moment derivatives due to a,b and c,respectively;andCmacan be approximately regarded to be zero.13The moment and lift arose by wind gust can be given by14

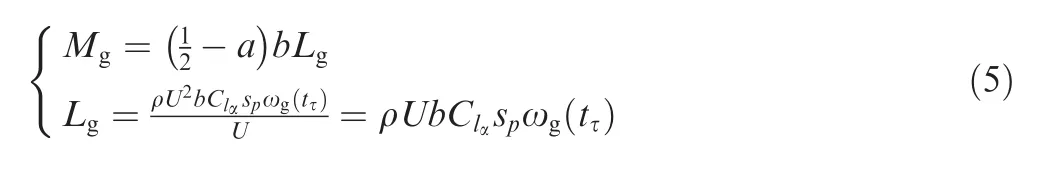
wherets?Ut=b,and xgetsT denotes the disturbance velocity.

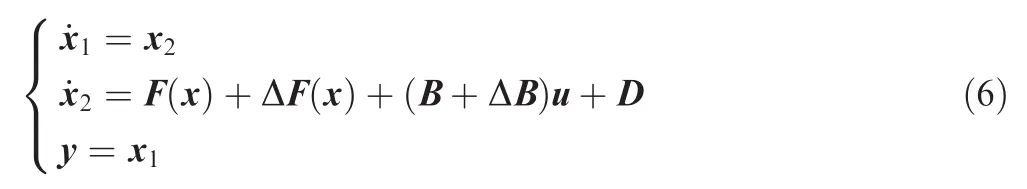
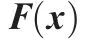
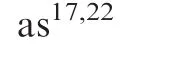
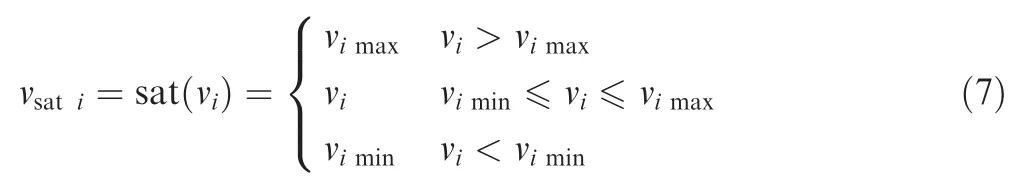
wherevimaxandvimindenote the known saturation values of the control inputvi(i?1;2).

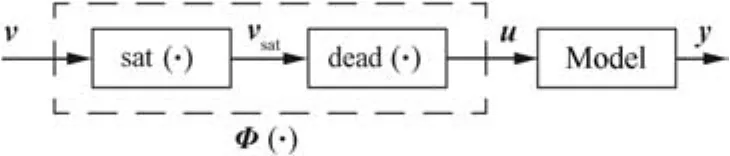
Fig.2 Structural diagram of input nonlinearity

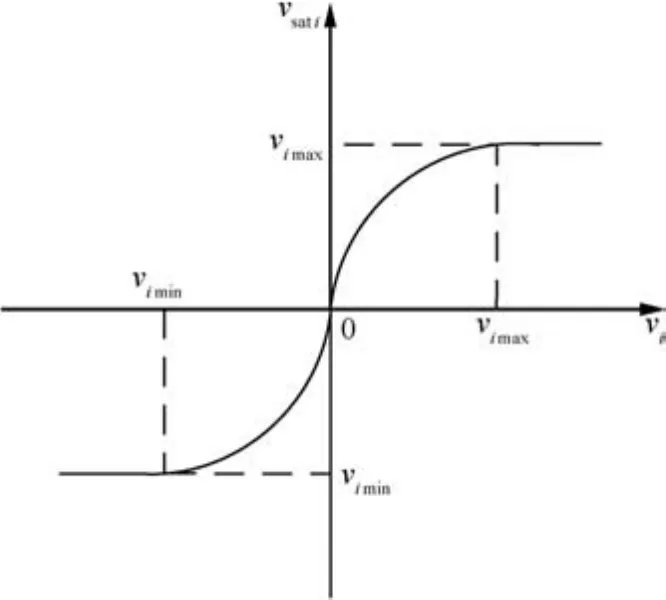
Fig.3 Saturation function

Fig.4 Dead-zone function

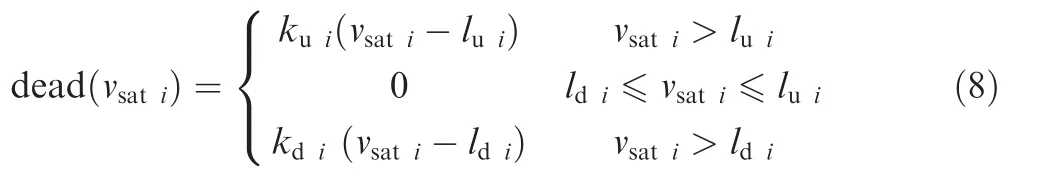
whereluiandldiare the breakpoints of the dead-zone;kui>0 andkdi>0 are the right and left slope parameters,respectively.

In this paper,the control objective is to design a constrained adaptive neural network controller for the MIMO aeroelastic system in Eq.(6)to ensure the output y can track the desired output signal ydby appropriately choosing design parameters.

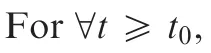
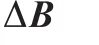
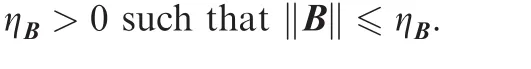
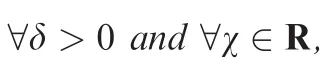
Lemma 320.No eigenvalue of matrixAexceeds any of its norm in its absolute value,that is,

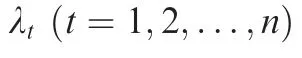
2.2.Analysis of input nonlinearity

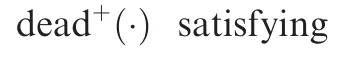
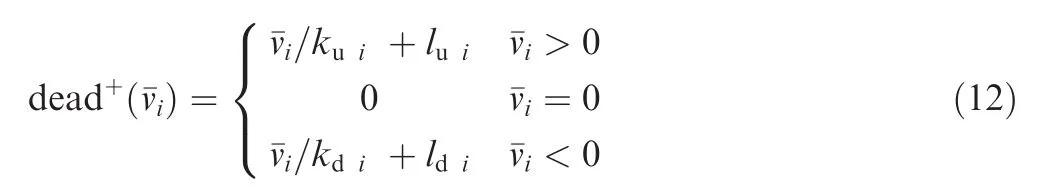
Base on the analysis of the characteristics of the new construction of input nonlinearity in Ref.26,uican be described as

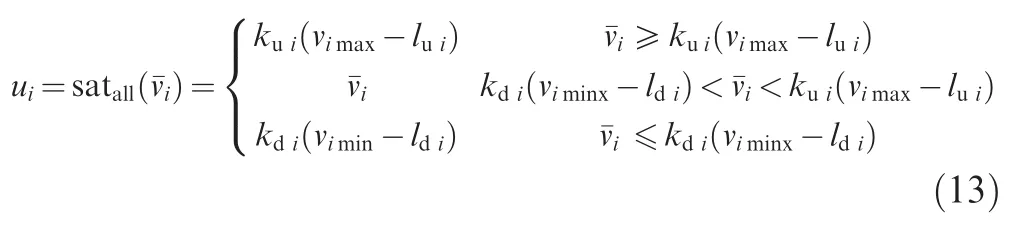
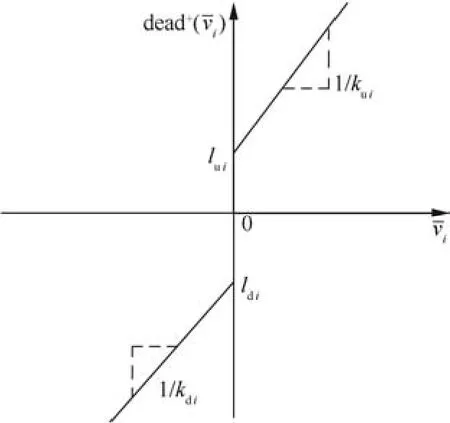
Fig.5 Right inverse function

Fig.6 Structural diagram of input nonlinearity

The above equation means that the input saturation and dead-zone coupled with the right inverse function block of the dead-zone can be regarded as an equivalent input saturation.

2.3.RBF neural networks

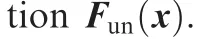
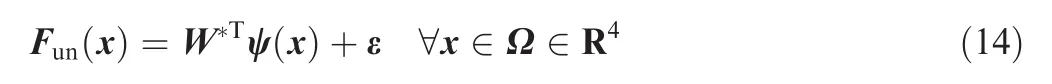
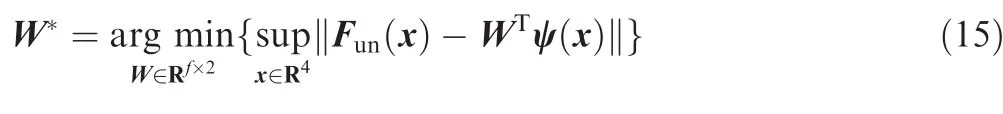
3.Design of a constrained adaptive control scheme based on RBFNNs

3.1.Design of a constrained adaptive control scheme

In this section,the backstepping method is used to construct a constrained adaptive neural network controller for the nonlinear system in Eq.(6).Define the error variables as

During the constrained adaptive neural network controller design,the backstepping control technique is employed and the detailed design process is described as follows.

Step 1.Considering the system in Eq.(6)and differentiating z1,we obtain

To proceed with the design of the constrained adaptive neural network control scheme,we define

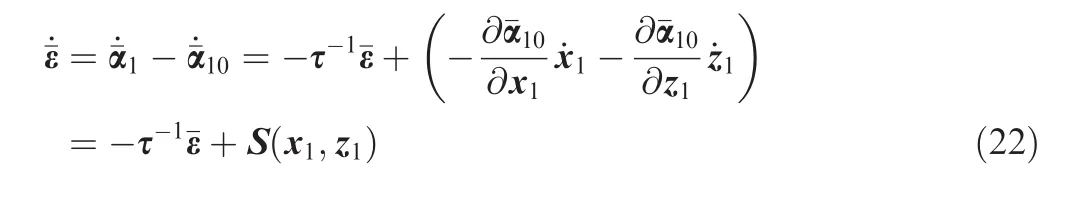
Then,we obtain

Consider the Lyapunov function candidate

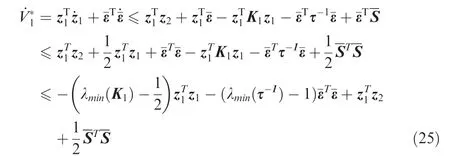
Step 2.Differentiating z2yields

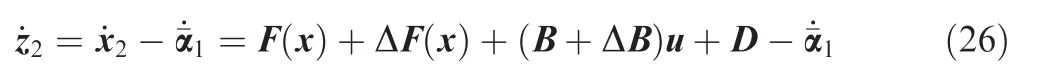
Consider the Lyapunov function candidate

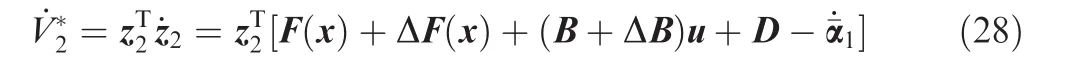
As shown in Section 2.3,the RBFNNs will be employed to approximate the system uncertainties DFexT,and the optimal approximation can be written as

Substituting Eq.(29)into Eq.(28)yields

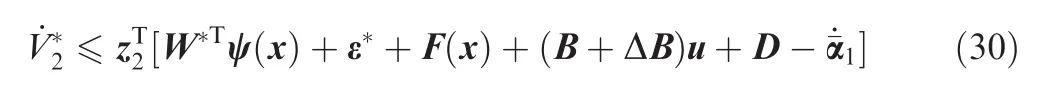
Considering Assumptions 1 and 2,we obtain

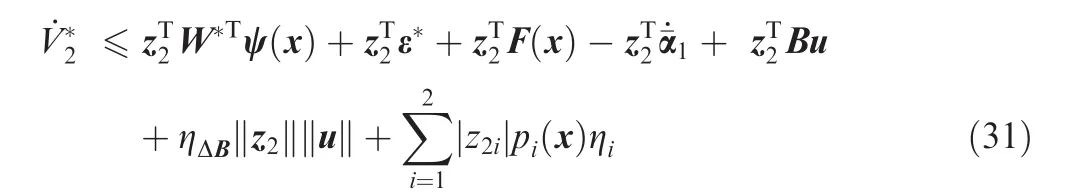
In view of Young’s inequality,20and invoking Lemma 1,Eq.(31)can be rewritten as

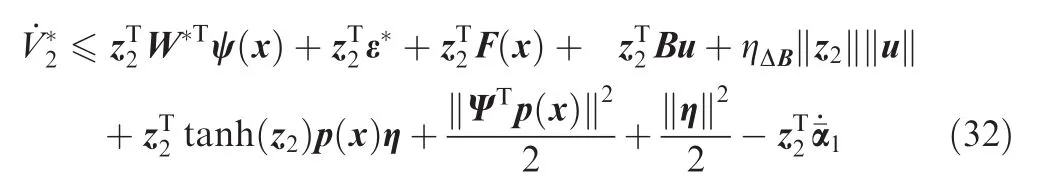
From Eq.(13),the control inputs u can be regarded as an input saturation problem.To compensate for the impact of the input saturation,the auxiliary error system is presented as follows20

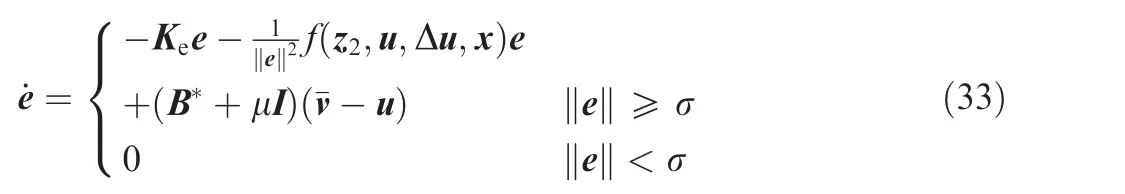
Define20

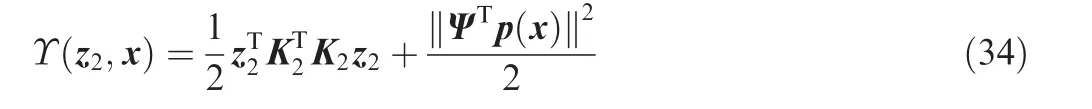
Invoking Lemma 2 and taking the input saturation into consideration,choose the control law as follows

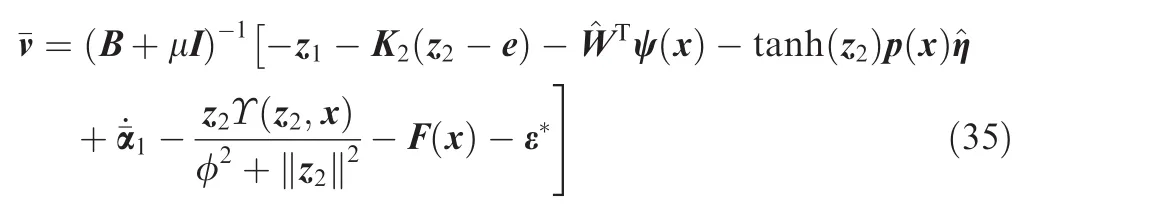
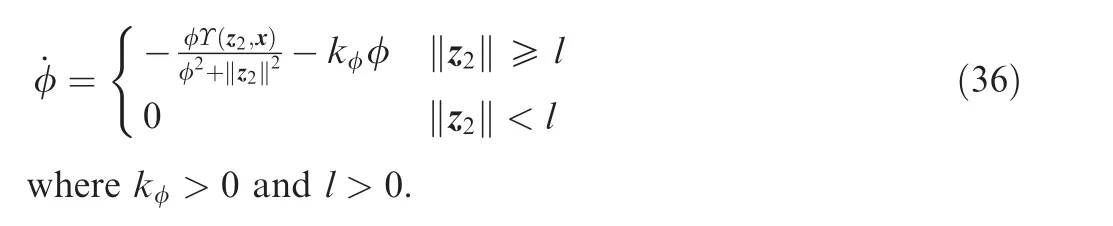
3.2.Stability analysis

In this section,the main results will be stated,and the semiglobal boundedness of all the signals in the closed-loop system will be proven by two cases.

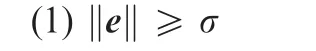
Choose the Lyapunov function as follows

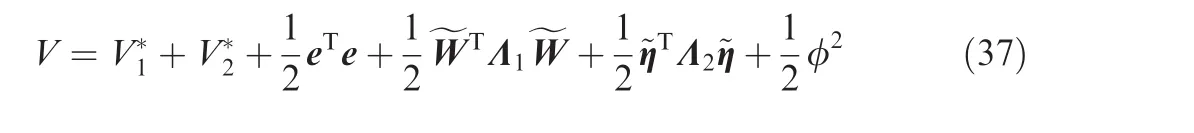
Following from Eqs.(25)and(32)and invoking Lemma 3,the time derivative ofVis

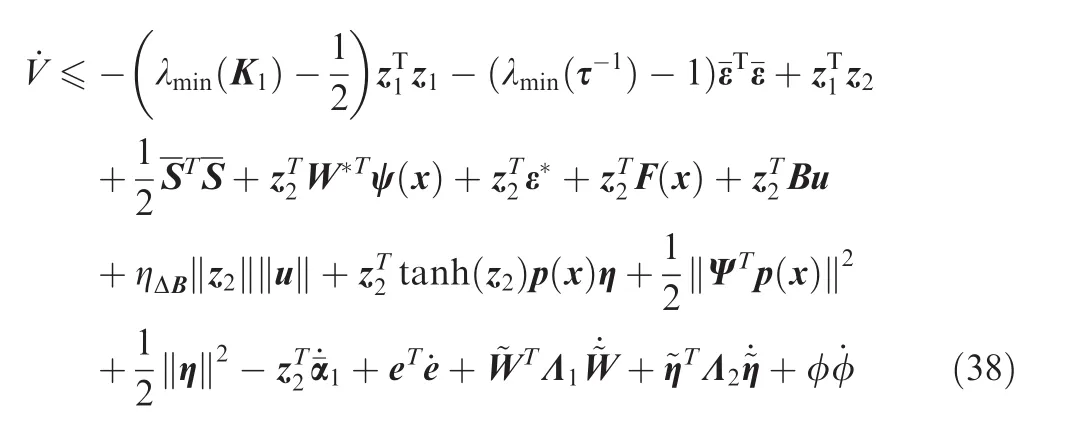
Invoking Eq.(36),we obtain

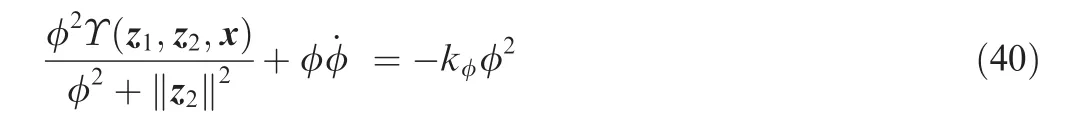
Substituting Eq.(40)into Eq.(39)yields

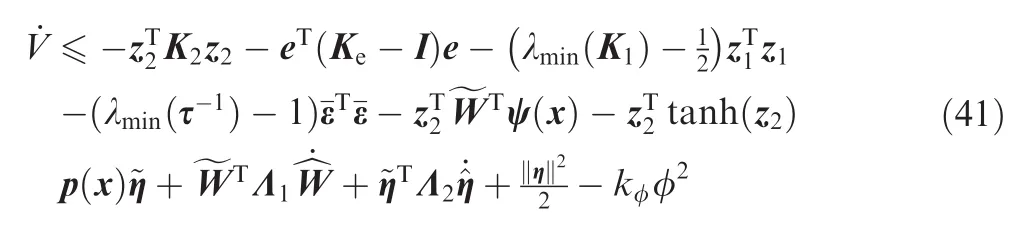
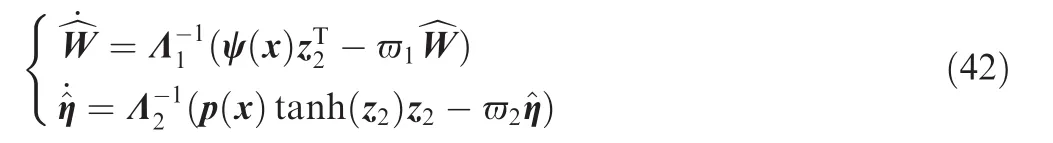
Substituting Eq.(42)into Eq.(41),we obtain

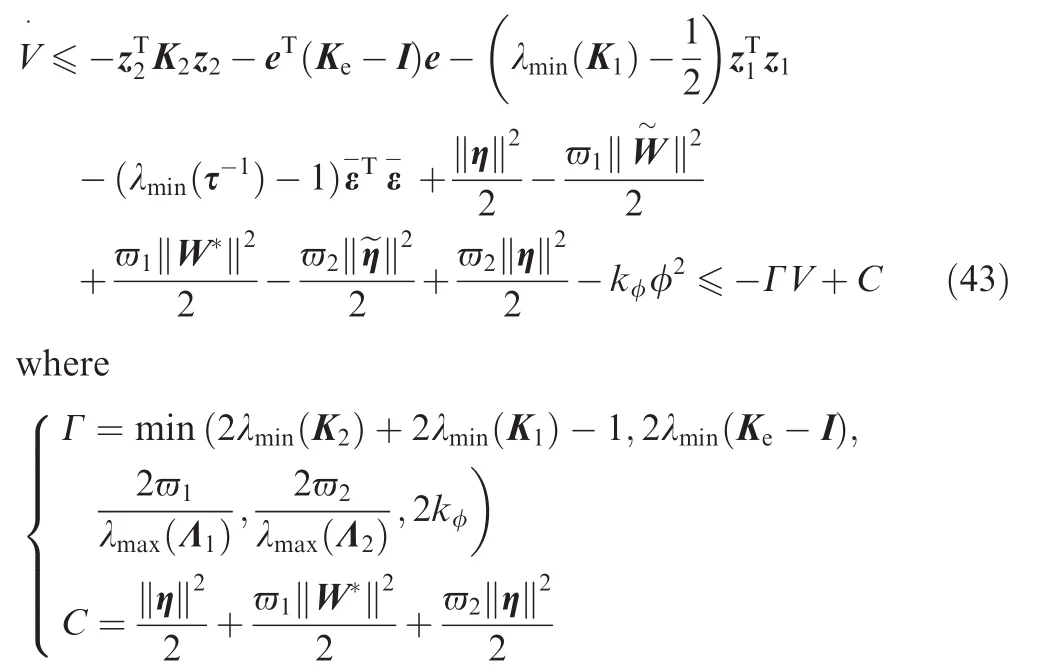
The structure diagram of the whole control system can be seen in Fig.7.

4.Example results and discussion

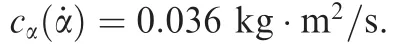
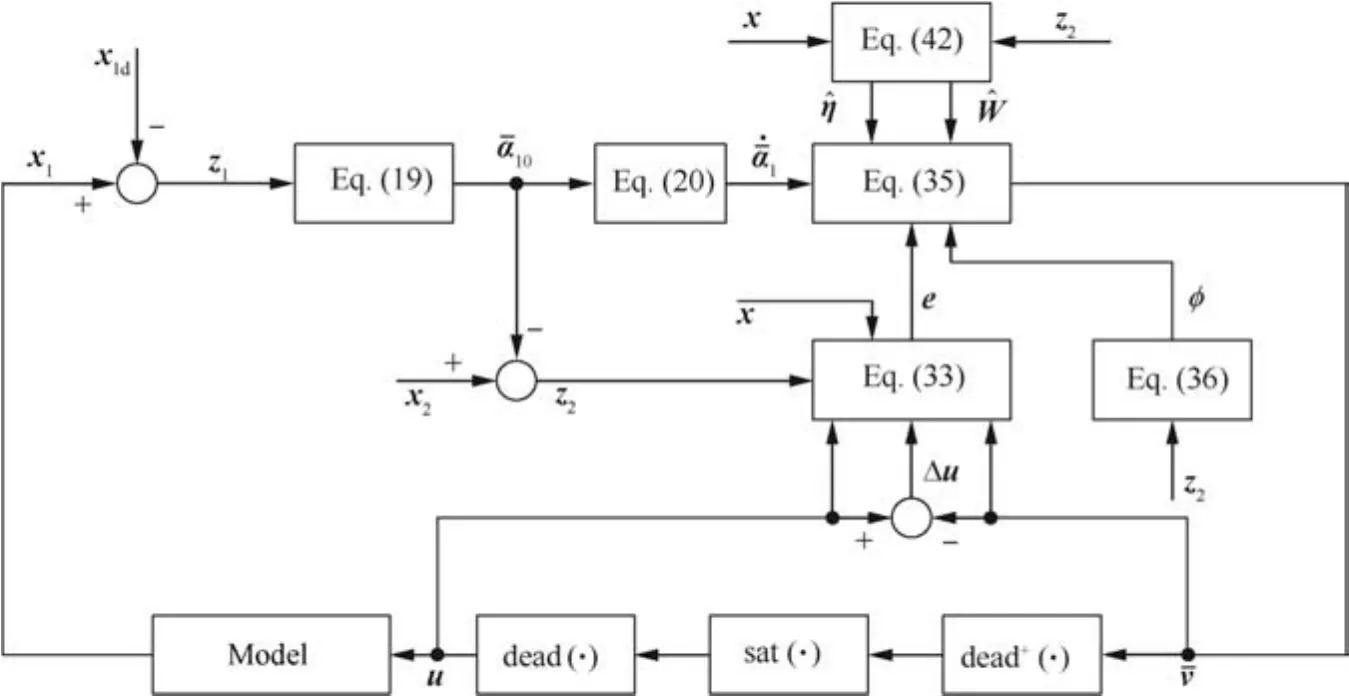
Fig.7 Structural diagram of whole control system.

For the purpose of examining the effectiveness of the proposed constrained adaptive neural network control scheme at different freestream velocities,simulations at three different freestream velocitiesUc,1:5Ucand 2Ucare undertaken.The results are presented in Fig.11,which shows that the closedloop system is stable despite different freestream velocities,and for a higher freestream velocity,the responses are quicker.To examine that the LCOs can be suppressed,the aeroelastic system at a freestream velocity of 12 m/s is held in an open loop for 10 s and then the loop is closed.In Fig.12,we can observe that the pitch LCO is suppressed in about 5 s and the plunge LCO is suppressed in about 1 s;in terms of control surface,the TE control surface deflection converges to zero in less than 6 s,and the LE control surface deflection converges to zero in about 2 s.

Table 1 Model parameters.13–15

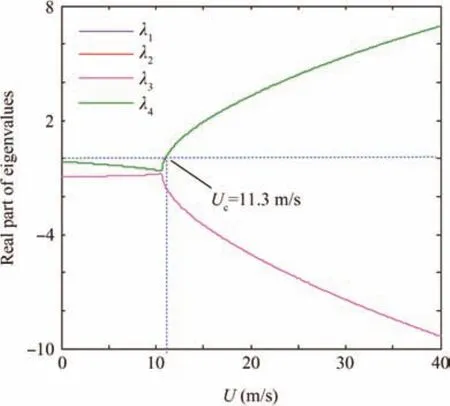
Fig.8 Real part of eigenvalues in open-loop system.

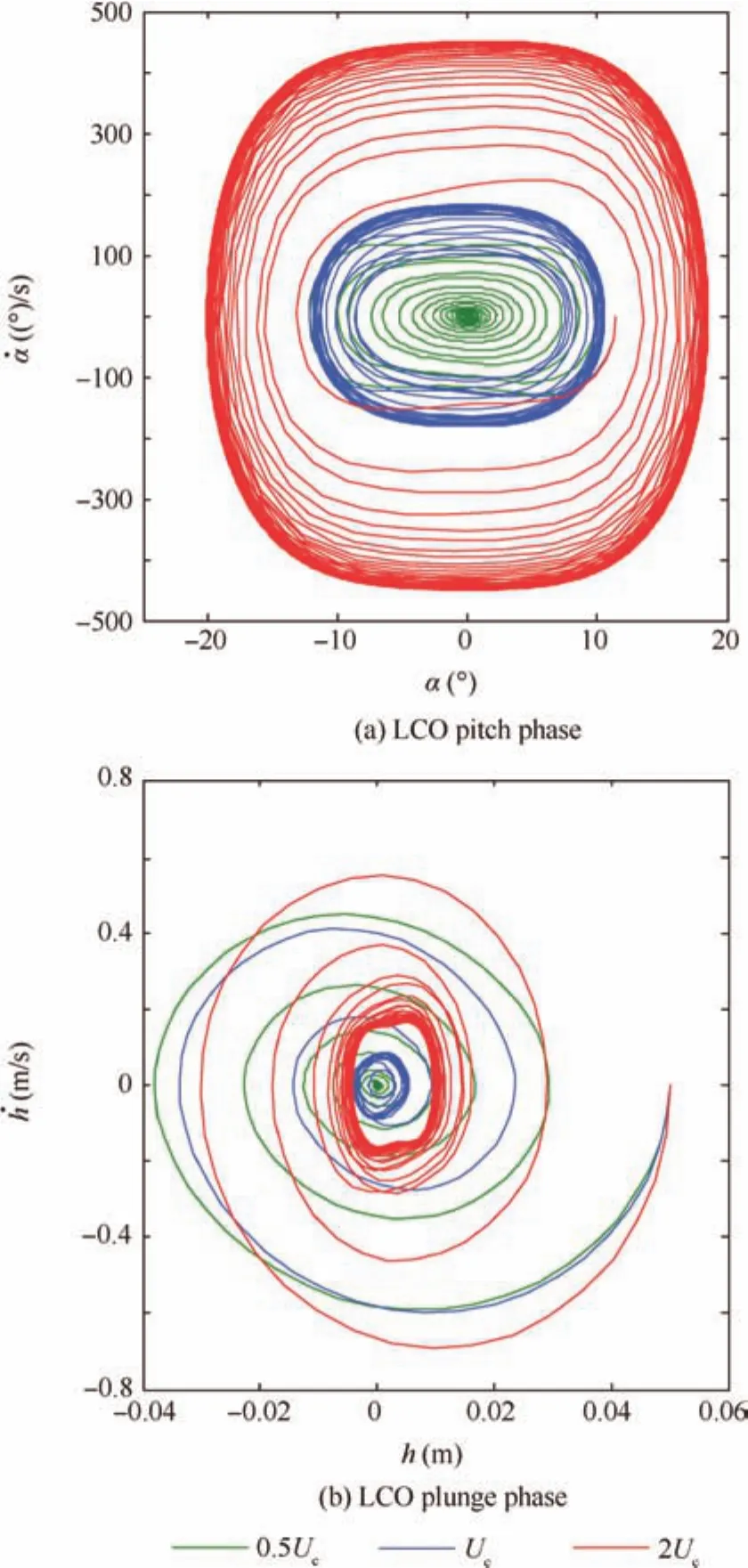
Fig.9 Aeroelastic system phase diagrams at different freestream velocities.

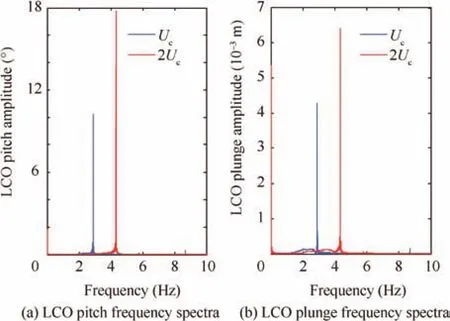
Fig.10 Aeroelastic system LCO frequency spectra at different freestream velocities.

To verify the applicability and robustness of the aeroelastic control system,based on four types of wind gust,four sets of simulations are done as follows.

The mathematical model of sinusoidal gust is given by14

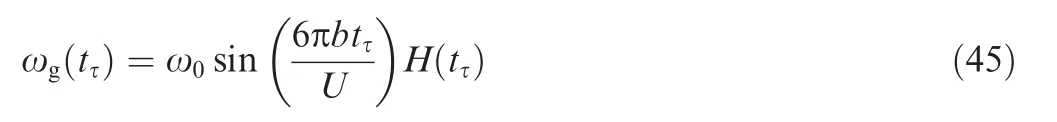
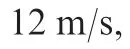
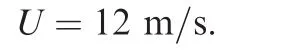
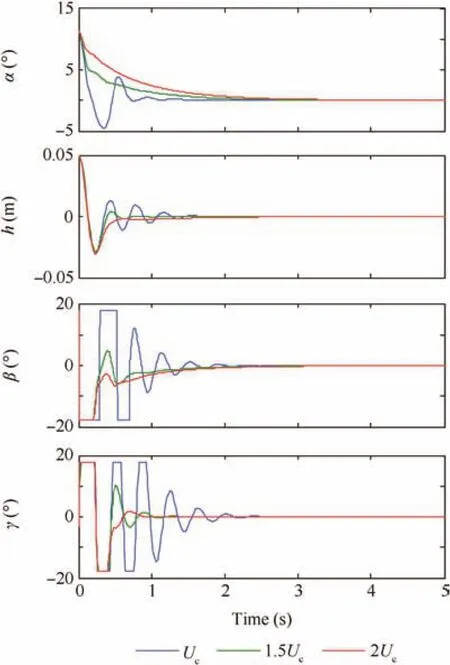
Fig.11 Constrained control at different freestream velocities.

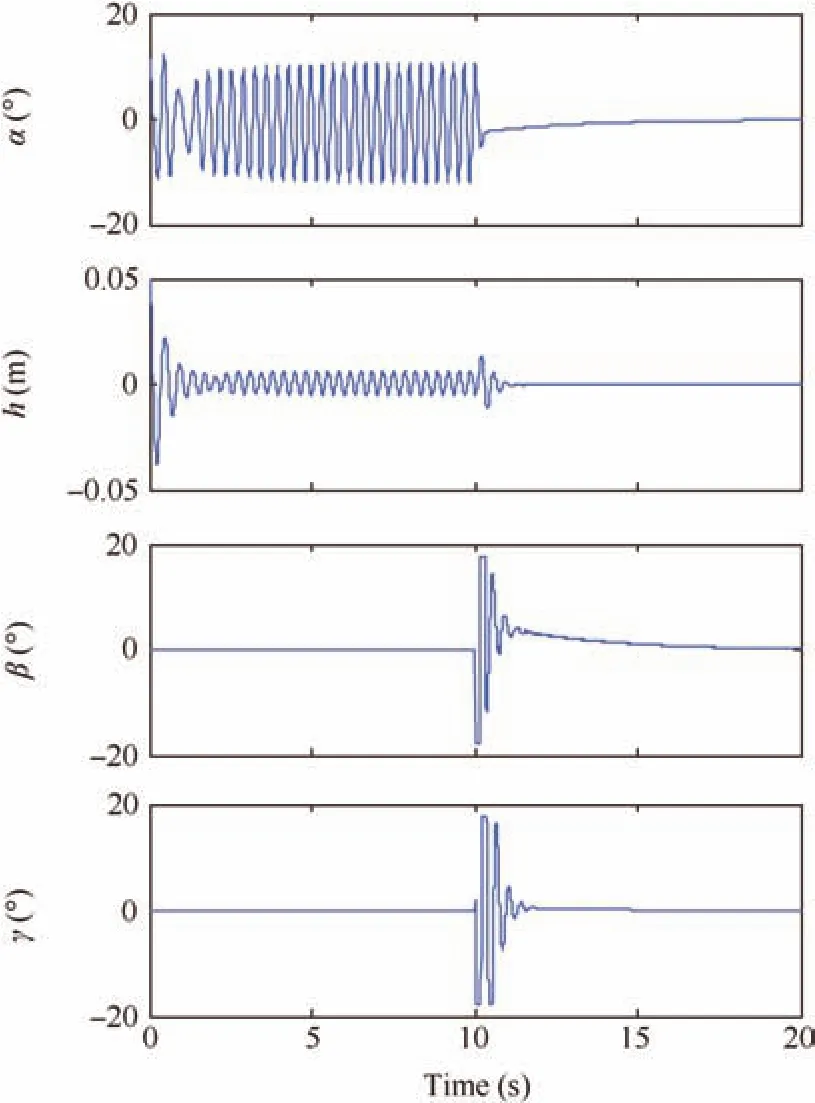
Fig.12 Constrained control,controller active at t=10 s.

Fig.13 Constrained control for sinusoidal gust,U?12 m=s.

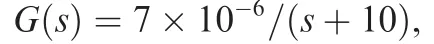
For the triangular gust,one has14

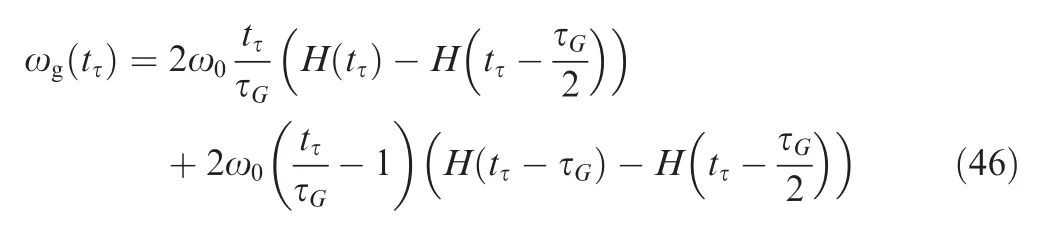
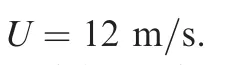
For the exponential gust,the mathematical model can be described as15

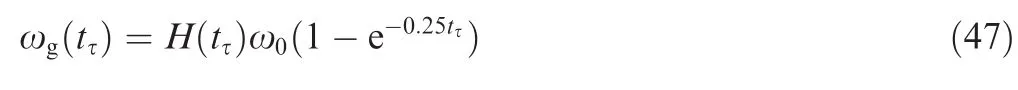
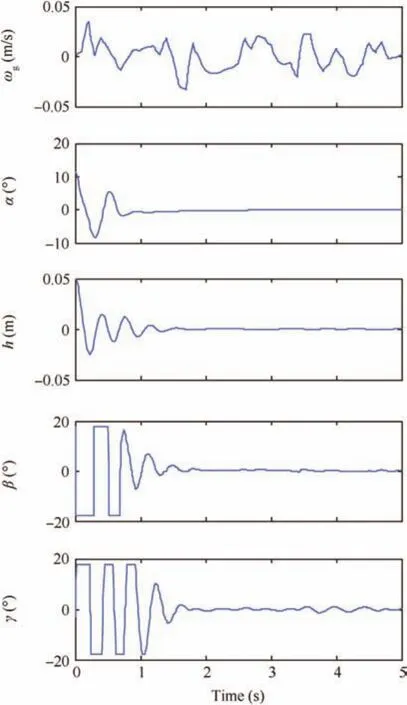
Figure 14 Constrained control for random gust,

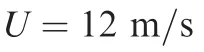
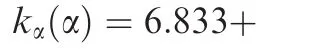
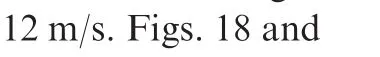
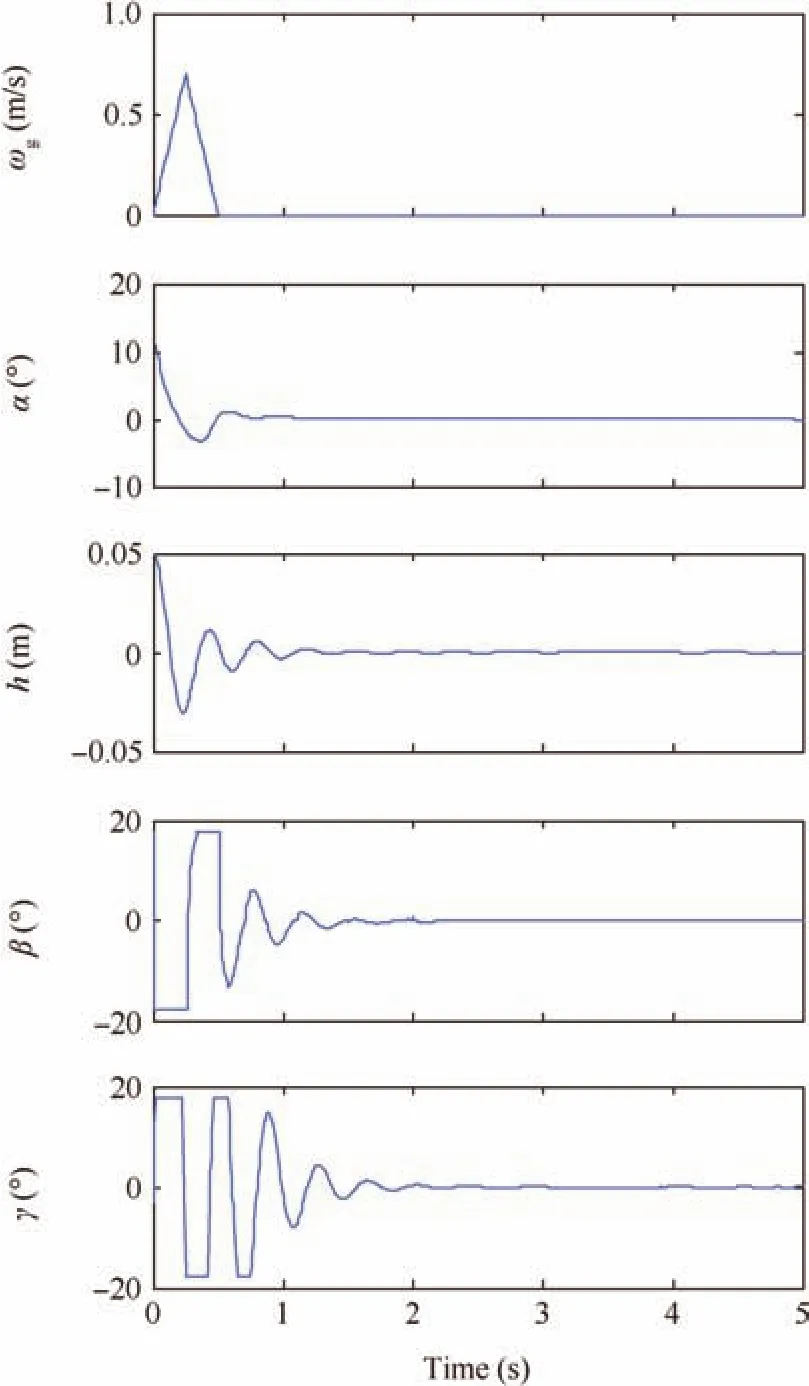
Fig.15 Constrained control for triangular gust,

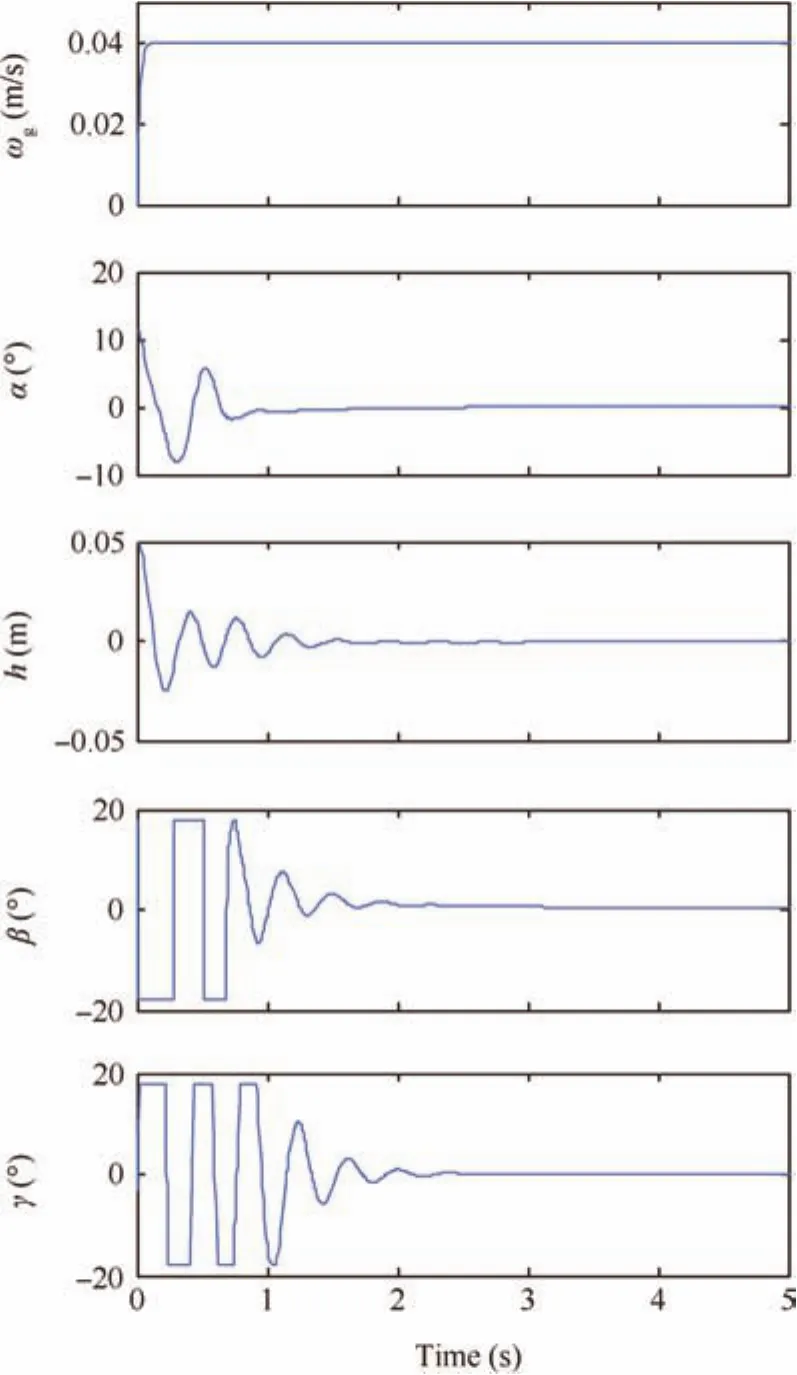
Fig.16 Constrained control for exponential gust,

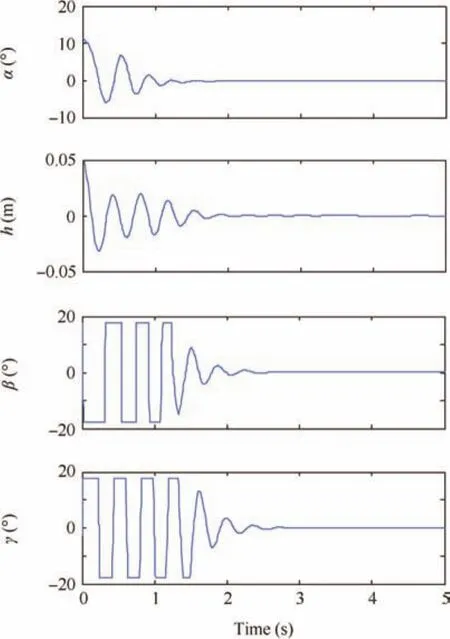
Fig.17 Constrained controlagainstsystem uncertainties,

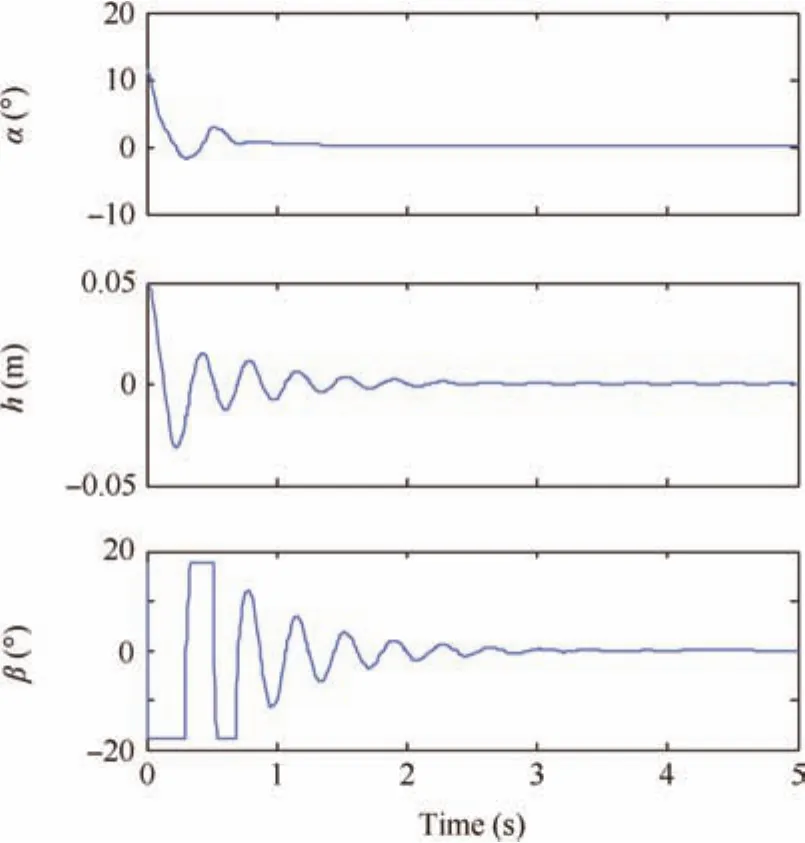
Fig.18 Constrained control with LE control surface failure,

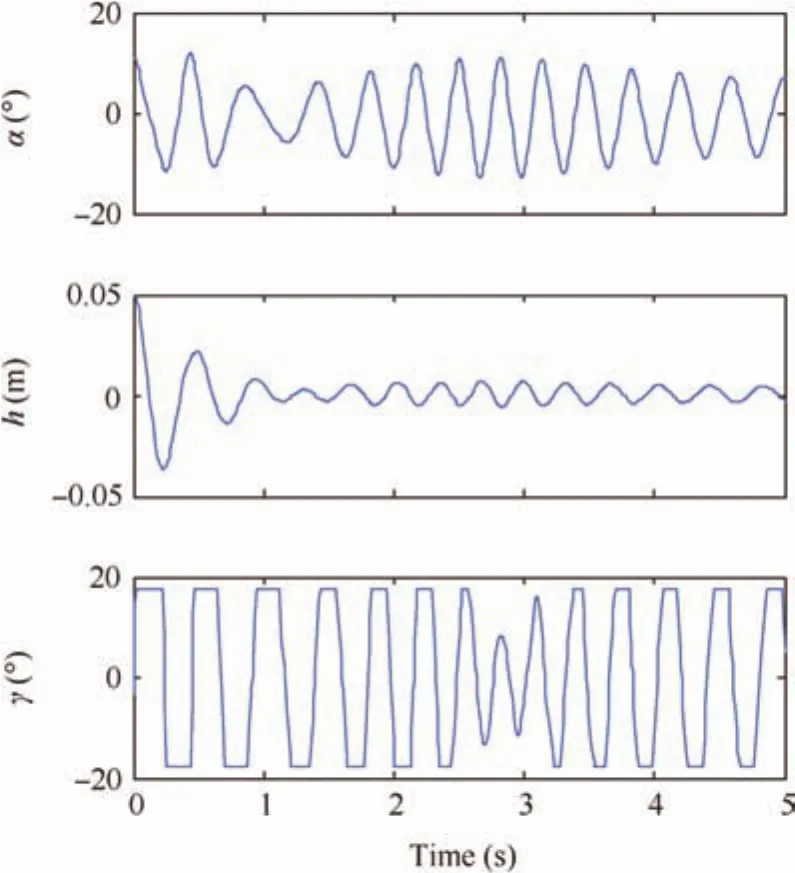
Fig.19 Constrained control with TE control surface failure,

5.Conclusions

(1)An effective constrained adaptive neural network control scheme has been developed for an MIMO aeroelastic system with wind gust,system uncertainties,and input nonlinearities.

(2)In order to handle the system uncertainties,RBFNNs have been employed to approximate the system uncertainties effectively,and simulation results demonstrate the effectiveness of the proposed control scheme against the system uncertainties.

(3)To deal with the input nonlinearities,the right inverse function block of the dead-zone is added before the input nonlinearities,and the input nonlinearities can be treated as a single input saturation nonlinearity.Moreover,an auxiliary error system is designed to compensate for the impact of the input saturation.

(4)By using the Lyapunov stability theory and the backstepping control technique,all signals of the closedloop system based on the proposed constrained adaptive neural network control scheme are semi-globally uniformly bounded.

(5)Digital simulation results illustrate the effectiveness of the proposed control scheme which can accomplish flutter suppression quickly at different freestream velocities.Moreover,in terms of wind gust,the simulation results verify the applicability and robustness of the proposed control scheme.In addition,considering the failure of a control surface,we find that the proposed control method can be applied to the aeroelastic system with only the TE control surface.

Acknowledgements

This research was supported by the National Natural Science Foundation of China(Nos.61473307 and 61304120),and the AeronauticalScience Foundation of China (No.20155896026).

1.Mukhopadhyay V.Historical perspective on analysis and control of aeroelastic responses.J Guidance,Control,Dyn2003;26(5):673–84.

2.Li DC,Xiang JW,Guo SJ.Adaptive control of a nonlinear aeroelastic system.Aerospace Sci Technol2011;15(5):343–52.

3.Lind R,Brenner M.Robust aeroservoelastic stability analysis.London:Springer-Verlag;1999.p.117–52.

4.Waszak MR.Robust multivariable flutter suppression for benchmark active control technology wind-tunnel model.J Guidance,Control,Dyn2001;24(1):147–53.

5.Mukhopadhyay V.Transonic flutter suppression control law design and wind-tunnel test results.J Guidance,Control,Dyn2000;23(5):930–7.

6.Kelkar AG,Joshi SM.Passivity-based robust control with application to benchmark controls technology wing.J Guidance,Control,Dyn2000;23(5):938–47.

7.Ko J,Kurdila AJ,Strganac TW.Nonlinear control of a prototypical wing section with torsional nonlinearity 1997.J Guidance,Control,Dyn1997;20(6):1181–9.

8.Ko J,Strganac TW,Kurdila AJ.Adaptive feedback linearization for the control of a typical wing section with structural nonlinearity.Nonlinear Dyn1999;18(3):289–301.

9.Xing W,Singh SN.Adaptive output feedback control of a nonlinear aeroelastic structure.J Guidance,Control,Dyn2000;23(6):1109–16.

10.Lee KW,Singh SN.Global robust control of an aeroelastic system using output feedback.J Guidance,Control,Dyn2007;30(1):271–5.

11.Beha A,Marzocca P,Rao VM,Gnann A.Nonlinear adaptive control of an aeroelastic two-dimensional lifting surface.J Guidance,Control,Dyn2006;29(2):382–90.

12.Platanitis G,Strganac TW.Control of a nonlinear wing section using leading-and trailing-edge surfaces.J Guidance,Control,Dyn2004;27(1):52–8.

13.Gujjula S,Singh SN,Yim W.Adaptive and neural control of a wing section using leading-and trailing-edge surfaces.Aerospace Sci Technol2005;9(2):161–71.

14.Wang Z,Behal A,Marzocca P.Model-free control design for multi-input multi-output aeroelastic system subject to external disturbance.J Guidance,Control,Dyn2011;34(2):446–58.

15.Lee KW,Singh SN.Adaptive control of multi-Input aeroelastic system with constrained inputs.J Guidance,Control,Dyn2015;38(12):2337–50.

16.Lee KW,Singh SN.Robust higher-order sliding-mode finite-time control of aeroelastic systems.J Guidance,Control,Dyn2014;37(5):1664–70.

17.Chen M,Ge SS,Eehow BV.Robust adaptive neural network control for a class of uncertain MIMO nonlinear systems with input nonlinearities.IEEE Trans Neural Netw2010;21(5):796–812.

18.Zhou J,Wen C,Zhang Y.Adaptive output control of nonlinear systems with uncertain dead-zone nonlinearity.IEEE Trans Autom Control2006;51(3):504–10.

19.Tong S,Li Y.Adaptive fuzzy output feedback control of MIMO nonlinear systems with unknown dead-zone inputs.IEEE Trans Fuzzy Sys2013;21(1):134–46.

20.Chen M,Ge SS,Ren BB.Adaptive tracking control of uncertain MIMO nonlinear systems with input constraints.Automatica2011;47(3):452–65.

21.Li Y,Tong S,Li T.Adaptive fuzzy output feedback control for output constrained nonlinear systems in the presence of input saturation.Fuzzy Sets Syst2014;248(1):138–55.

22.Yang QY,Chen M.Adaptive neural prescribed performance tracking control for near space vehicles with input nonlinearity.Neurocomputing2016;174:780–9.

23.Liu ZC,Dong XM,Xue JP,Chen Y.Adaptive neural control for a class of time-delay systems in the presence of backlash or deadzone nonlinearity.IET Control Theory Appl2014;8(11):1009–22.

24.Zhang TP,Ge SS.Adaptive dynamic surface control of nonlinear systems with unknown dead-zone in pure feedback form.Automatica2008;44(7):1895–903.

25.Polycarpou MM,Ioannou PA.A robust adaptive nonlinear control design.Automatica1996;32(3):423–7.

26.Ma DCRL,Heath WP.Controller structure for plants with combined saturation and deadzone/backlash.2012 IEEE international conference on control application;2012 Oct 18–20;Dubrovnik.Piscataway(NJ):IEEE Press;2012.p.1394–9.

27.Chen M,Yu J.Adaptive dynamic surface control of NSVs with input saturation using a disturbance observer.Chin J Aeronautics2015;28(3):853–64.

20 April 2016;revised 2 September 2016;accepted 28 November 2016

Available online 16 February 2017

*Corresponding author.

E-mail addresses:gouyiyong@139.com(Y.Gou),dongxinmin@139.com(X.Dong).

Peer review under responsibility of Editorial Committee of CJA.