矩陣乘法在斐波那契數列計算中的應用

周衛星 陳思 張帆

（中國移動（深圳）有限公司，廣東深圳518048）

矩陣乘法在斐波那契數列計算中的應用

周衛星 陳思 張帆

（中國移動（深圳）有限公司，廣東深圳518048）

本文介紹了斐波那契數列的一些算法思路，對遞歸算法、自底向上、比內公式等算法的時間復雜度進行了分析，給出了利用矩陣乘法升維計算降低時間復雜度的方法，對比測試了各算法實現在不同計算量下的執行時間。針對數據溢出，將long數據類型改進為BigInteger的數據類型,給出了大數計算下的執行時間對比。

斐波那契；遞歸；比內公式；矩陣

1 引言

斐波那契數列（Fibonacci sequence），又稱黃金分割數列，因數學家列昂納多·斐波那契（Leonardoda Fibonacci）以兔子繁殖為例子而引入，故又稱為“兔子數列”。它指的是這樣一個數列：1、1、2、3、5、8、13、21、34、……這個數列從第3項開始，每一項都等于前兩項之和。在數學上，斐波納契數列被以遞歸的方法定義如下：

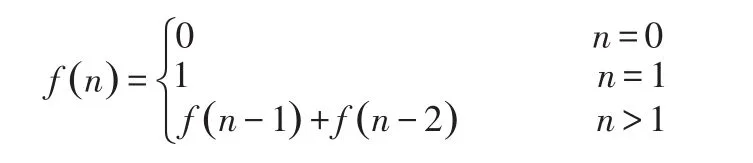
2 直接遞歸實現

使用公式f(n)=f(n-1)+f(n-2)，依次遞歸計算，遞歸結束條件是f(1)=1，f(2)=1。

核心代碼如下：

這種方式可以以非常少的代碼實現第N+1項的計算，但是與之相對的，這種算法的代價也非常高，計算機每次調用函數時，為了保證函數執行完畢，都必須將函數調用時的程序現場入棧保存，遞歸存在大量的自身調用，勢必會產生非常龐大的函數現場棧來記錄數據。

以求解f(10)作為例子來分析遞歸求解的過程。要求得f(10)，需要求得f(9)和f(8)。同樣，要求得f(9)，要先求得f(8)和f(7)……用樹形結構來表示這種依賴關系：

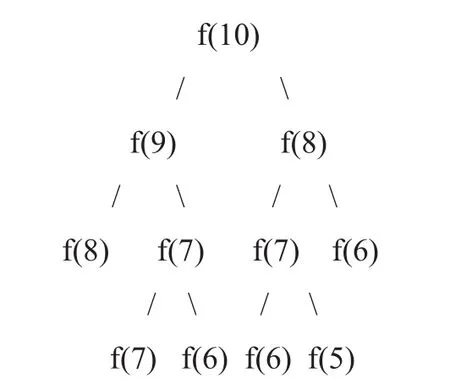
圖1 遞歸求解的樹形結構

不難發現在這棵樹中有很多結點會重復的，而且重復的結點數會隨著n的增大而急劇增加。這意味著計算量會隨著n的增大而急劇增大。用遞歸方法計算的時間復雜度是以n的指數的方式遞增的。

CPU為i52.5GHZ，8G內存，windows764位操作系統，使用System.nanoTime()來計算消耗時間，一輪計算十次取平均耗時，三輪的平均耗時如下（后續方法相同，不再贅述）：

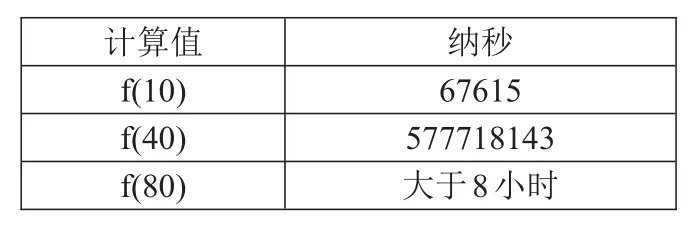
表1 直接遞歸實現在不同計算值下的執行時間

當計算f(80)時，超過8小時未計算出結果。

3 自底向上實現

上述直接遞歸算法，為了求解f(n)，需要同時遞歸求解f(n-1)和f(n-2)，顯然這樣就做了大量的重復工作。采用自底向上的算法即可避免這樣的冗余。從最小需計算的f(3)開始，逐步向上計算f(4)、f(5)等，將每步計算結果都保存下來，作為下次計算的初始值，要計算f(n)，則依次計算f(0)，f(1)，f(2)...f(n)，這時計算f(n)只需要利用前兩個結果即可，這樣算法效率提高到了O(n)。

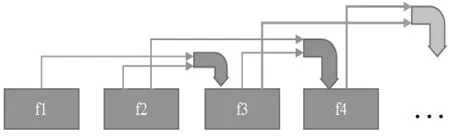
圖1 自底向上實現示意圖

3.1 動態數組

Arraylist能動態地增加和減少元素，使用它可以保存每次計算的結果，但是它每次執行add等添加元素的方法，都會檢查內部數組的容量是否不夠了，如果是，它會以當前容量的兩倍來重新構建一個數組，將舊元素copy到新數組，然后丟棄舊數組。因此效率不如數組，其核心代碼如下：

3.2 數組實現

與Arraylist類似，不過是將每次的計算結果保存到數組結構中，不再贅述。

3.3 swap實現

注意到以上兩種方式緩存空間僅用于兩次計算，因此可以使用新計算結果覆蓋原有空間，節省空間。

圖2 swap實現示意圖

其核心算法如下：

自底向上算法各實現方式的消耗時間對比情況如表2。

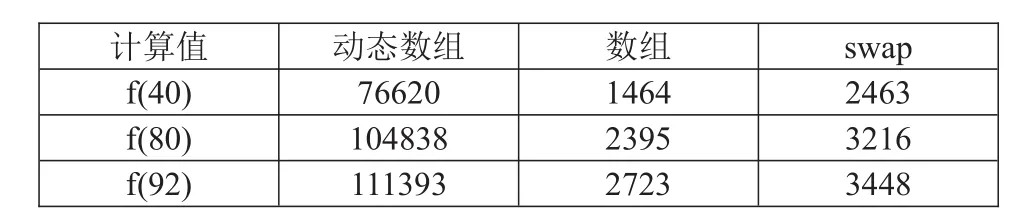
表2 自底向上實現在不同計算值下的執行時間

對比簡單遞歸實現，計算時間減少了不少，而且隨著計算值增大，節約時間越明顯。

同時也可以看到不同的實現方式耗時不同，時間復雜度與實際執行時間并不是絕對成正比關系。

4 比內公式實現

f(n)=f(n-1)+f(n-2)線性遞推數列的特征方程為：x2=x+1

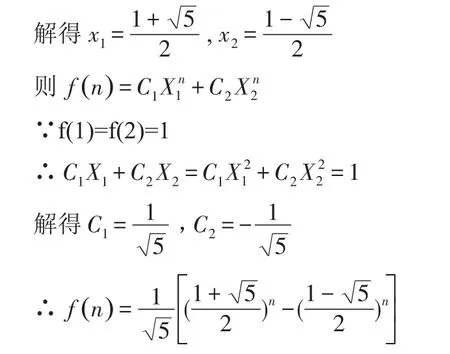
核心代碼為

代碼復雜度為O(1)，由于double類型的精度還不夠，所以程序算出來的結果會有誤差。

5 矩陣乘法實現

斐波那契數列的表達式可以寫成如下兩個形式：

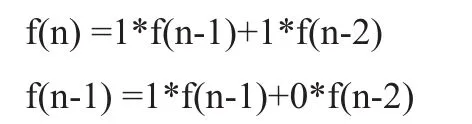
可以轉換為矩陣表達：

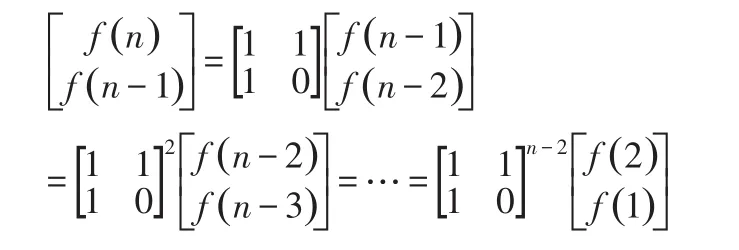
因此，成為了矩陣的乘方問題。

若A為n×k矩陣，B為k×m矩陣，則它們的乘積AB(有時記做A·B)將是一個n×m矩陣。前一個矩陣的列數應該等于后一個矩陣的行數，得出的矩陣行數等于前一個矩陣的行數，列數等于后一個矩陣的行數。

其乘積矩陣AB的第i行第j列的元素為：

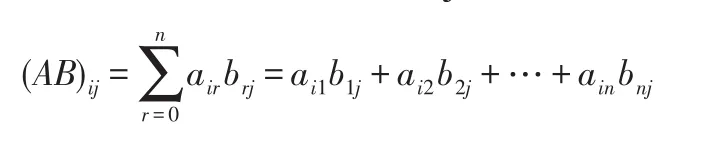
通過分治法或快速冪，算法效率提高到了O(logn)。所謂分治法就是：

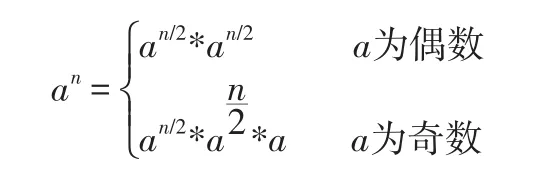
快速冪就是利用結合律快速計算冪次的方法，應用到矩陣即可：

當n越大，相比較其他算法會節省更多時間。核心代碼為矩陣乘法與分治法（或快速冪），此處不細述。

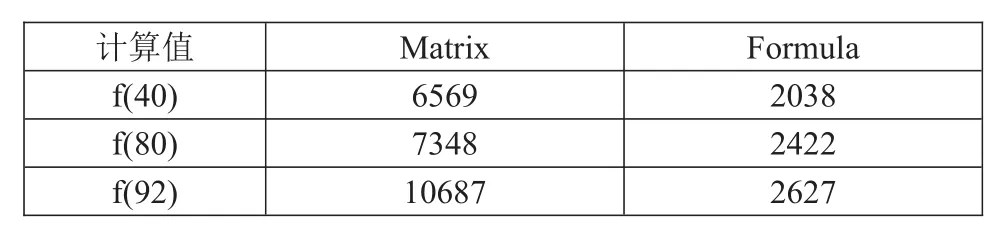
表3 比內公式和矩陣乘法實現在不同計算值下的執行時間

以上使用基本類型long，當n＞92時，會超出long的表達范圍，因此結果不正確，此時需要用BigInteger解決溢出問題，但會比long耗時多一些。

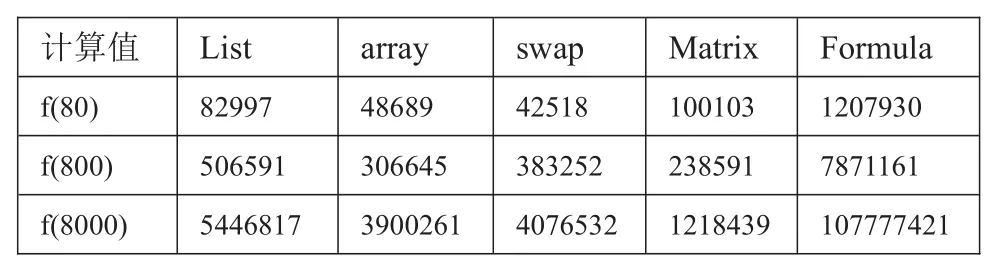
表4 各算法實現在BigInteger類型下的執行時間

可以看到計算值從f(80)到f(800)到f(8000)，10倍的增長，但矩陣法耗時并沒有隨著線性增長，性能最佳。

由于公式法小數需要使用BigDecimal，效率降低了很多，f(800)結果達到了10167，公式法精度存在問題，取整后結果已然不對，保留10000位小數時僅能保證前13位正確，f(8000)結果更是達到了101672的數量級。

6 結束語

直接使用遞歸算法雖能快速寫出，且容易理解，但其耗費空間和時間都很大，使用自底向上算法可以將時間復雜度降低到O(n)，使用推導出來的公式雖能將時間復雜度降低到O(1)，但冪方運算依然耗時，而且在大數下無法保證精度。通過升維到二維矩陣計算，可以將時間復雜度降低到O(logn)，在數據比較大的情況下，節省時間比較明顯。

[1] 李亞梅．遞歸算法的分析與應用[J]．中國新通信，2012，14(15)：89-90．

[2] 朱振元，朱承．遞歸算法的非遞歸化實現[J]．小型微型計算機系統，2003(03)：567-570．

[3] 王瑾瑜．斐波那契數列的幾種解法介紹及優缺點分析[J]．科技創新導報，2008(30)：241．

[4] 張新娟．斐波那契數列通項公式的求法[J]．高等數學研究，2009，12(04)：56-59．

[5] 彭軍．數據結構與算法[M]．北京：人民郵電出版社，2013．

[6] 潘金貴．算法導論[M]．齊德昱編著．北京：清華大學出版社，2003．

Application of Matrix Multiplication in Fibonacci Sequence Calculation

Zhou WeixingChen SiZhang Fan
(China Mobile(Shenzhen)Limited,Shenzhen 518048,Guangdong）

This paper introduces some algorithms of Fibonacci sequence calculation,analyzes the time complexity of recursive,bottom-up and Binet formula algorithms,gives a method to reduce the time complexity by using two dimension matrix multiplication,and compares the execution time of different amount of calculation among these algorithms.It modifies the long data type to BigInteger data type to resolve the data overflow problem,and compares different algorithms’execution time for large number calculation.

Fibonacci;recursive;Binet formula;matrix

TP311.1

A

1008-6609 (2017) 09-0071-03

周衛星(1991-)，男，湖南永州人，碩士研究生，軟件開發工程師，研究方向為J2EE架構、圖像識別、計算機網絡。