采用空間編碼與正弦選擇算子遺傳算法求解排課問題?

錢海軍

（珠海城市職業技術學院 珠海 519000）

采用空間編碼與正弦選擇算子遺傳算法求解排課問題?

錢海軍

（珠海城市職業技術學院 珠海 519000）

遺傳算法是求解多約束、多目標組合優化問題的有效算法。經典遺傳算法具有早熟特性，可以直接導致算法陷入局部最優解。為了提高算法的全局搜索性能，以遺傳算法的染色體編碼設計和選擇算子設計兩個方面為切人點，提出基于空間編碼與正弦選擇算子遺傳算法（SCSS）。仿真實驗證明，SCSS遺傳算法求解開放教育排課問題能夠滿足多重約束條件，為有效實現排課問題的智能求解提供實用性的數學方法。改進后的遺傳算法能夠快速收斂得到問題的全局最優解，算法全局搜索性能明顯增強。

遺傳算法；多約束；空間編碼；正弦選擇算子；開放教育；全局最優解

1 引言

由美國Michigan大學Holland教授于1975年首次提出的遺傳算法［1］是求解最優化問題的經典方法之一［2］。該算法對于非線性、大規模、單峰函數、多峰多態函數的求解都可以獲得較好的結果。遺傳算法是一種模擬自然選擇、物種進化的全局優化搜索技術。其優點是采用種群搜索技術在解空間進行全局搜索以獲得全局最優解。遺傳算法通過對種群隨機產生的一組個體進行選擇、交叉、變異三種遺傳算子實現種群進化。選擇算子是根據個體適應度值來確定個體進行交叉和變異操作，適應度值高個體的則被選擇進行迭代進化，反之被淘汰；借助生物種群遺傳信息的概念，交叉算子通過染色體編碼在整個解空間進行有效搜索，將選擇的父代個體進行基因重組，交換兩個個體的基因座，從而產生大量的新個體。交叉的過程能夠增強最優個體的出現幾率，提高全局搜索能力的同時降低對有效模式的破壞概率。變異算子是通過模擬生物遺傳和進化過程中的變異環節實現對個體的變異，這個過程是新個體產生的重要原因之一［3］。變異算子在交叉算子的基礎上對產生的新個體內部基因進行微調，維持種群的多樣性［4］，使算法還具有一定的局部搜索能力。

2 算法改進

實踐證明，經過一定的迭代之后，種群的多樣性將有所降低，遺傳算法出現過早收斂［5］，較容易產生局部最優解。國內外學者針對算法內部的每個環節進行了大量研究，并提出了諸多有效地改進方法［6～8］。本文在借鑒上述研究成果的基礎上，從染色體編碼方式與選擇算子改進兩個方向為切入點，提出一種改進的遺傳算法。

2.1 三維空間編碼設計

通過分析，經典的遺傳算法采用二進制染色體編碼方式，在變異操作過程中，二進制編碼的各個基因座權重不同，導致變異的基因座越靠向高位，編碼串的改變量越大，則變異后越容易丟失最優個體［9］。本文基于經典遺傳算法的原理，結合開放大學遠程開放教育教學特征與排課問題的數學模型，提出基于三維空間的遺傳算法染色體編碼方案。

2.1.1 排課問題數學建模［10］

1）根據開放教育教學特征，建立排課問題數學模型，假設：

教師集合 Professors=｛J1，J2，…，Jm，…，JM｝，其中，1≤m≤M ；

教室集合 Classrooms=｛R1，R2，…，Rp，…，RP｝，其中，1≤p≤P；教室可容納人數Y；

課程集合 Courses=｛C1，C2，…，Cs，…，CS｝，其中，1≤s≤S；

時間集合 Times=｛T1，T2，…，Tq，…，TQ｝，其中，1≤q≤Q；

班級集合 Stugroups=｛G1，G2，…，Gn，…，GN｝，其中，1≤n≤N ；班級人數X=｛x1，x2，…，xn，…，xN｝；

2）排課問題屬于一種非線性、資源時空組合問題，建立硬約束條件［11］，如表1所示。

表1 遠程開放教育排課問題硬約束條件

3）建立排課問題軟約束條件［11］。

S1：教學效果較好的時間段安排較重要的課程，可以有效提高教學質量。開放教育教學安排的一般在周一至周五晚上，周六、周日全天。由于成人參與學習的特點，可以認為到課率較高的時間，教學效果也較好。數據分析可知，除周末外，教學質量較好的時間序列為：星期一、星期四、星期二、星期三、星期五。

假設 αi(i=1，2，3，4，5)表示授課時間段的優先級；數學描述如表2所示。

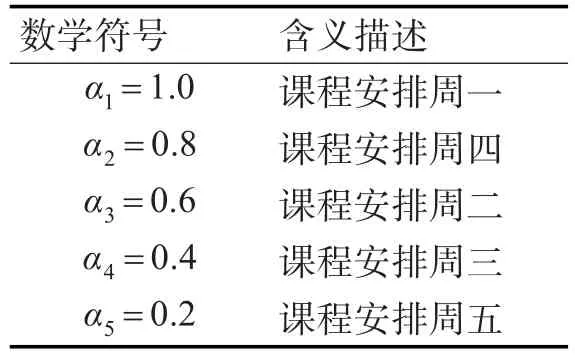
表2 S1軟約束條件變量

假設 βj(j=1，2，3，4，5，6)表示課程重要程度，其中：“1”表示通識課，“2”表示專業拓展課，“3”表示綜合實踐、“4”表示專業課，“5”表示專業基礎課，“6”表示公共基礎課。則優化目標為

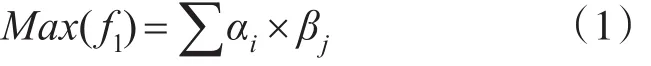
S2：滿足部分教師提出的課程安排的要求。假設職稱的級別系數為 εi(i=1，2，3)，“1”表示高職職稱，”2”表示中級職稱，”3”表示初級職稱；教師在規定時間段上課的意愿程度系數為δj(j=0，1，2)，其中“2”表示愿意，“1”表示可以接受，“0”表示不愿意；則優化目標為

S3：多學時課程授課時間應保證一定的間隔時間。假設一門課程的授課時間間隔為i天的教學效果系數為 λi(i=1，2，3，4，5)，設定1，2，3，4，5天的系數值分別為1，4，5，3，2，βj為課程的權重。則優化目標為

S4：同一課表，班級課程安排盡量保證均勻分布。某班級周課時分布均勻程度為

其中，ed表示班級GN在第d周上課的課時數，N表示班級的總數，則優化目標為

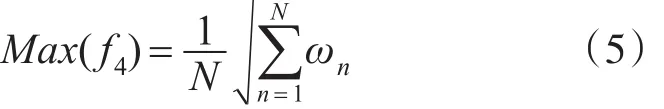
S5：教室利用率最大化，即根據班級學生的人數分配教室。假設班級人數XN與教室可容納的學生人數為YS的比值等于1，則教室利用率越高。約束條件優化目標為

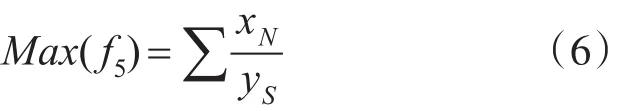
2.1.2 染色體編碼設計

開放教育專業規劃能夠確定排課問題數學模型中的教師集合Professors、課程集合Courses與班級集合Stugroups。作為已知參數，三個集合可以被組合成一個課程元祖，用 CPS（Courses、Professors、Stugroups）描述。如圖1所示，空間三維坐標體系內，X軸為T（時間片），坐標值對應一周內11個教學時間段，即 X1～X11；Y軸為 R（教室），坐標值對應學校全部可用的教室總數R，即Y1～YR；Z軸代表一個課程元組CPS。

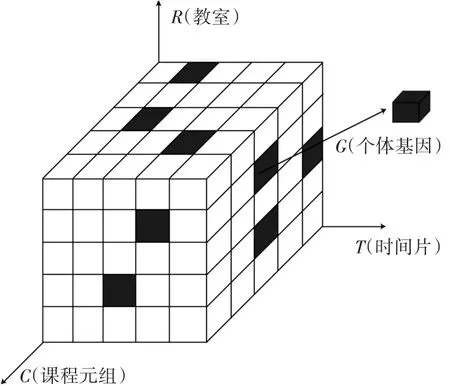
圖1 三維空間染色體編碼方案

從圖1可以看出，由空間三維坐標構成的黑色小立方體可以確定一個課程基因，該課程基因表示在某授課時間片TQ，某班級GN，在教室RP安排課程CS的授課事件。全部課程基因組成一條染色體，即表示一個課程表的排課方案。在時間片TQ和教室RP確定的條件下，課程基因（授課事件）數為

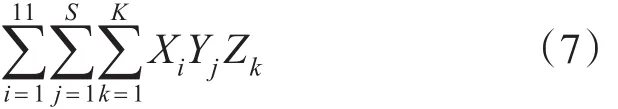
為了較直觀地描述該三維空間染色體編碼方案，將課程基因總數的求解映射為一個三維數組Timetable[][][]=｛(JM，GN，CS)，TQ，RP｝，圖形化描述該數據結構如圖2所示。

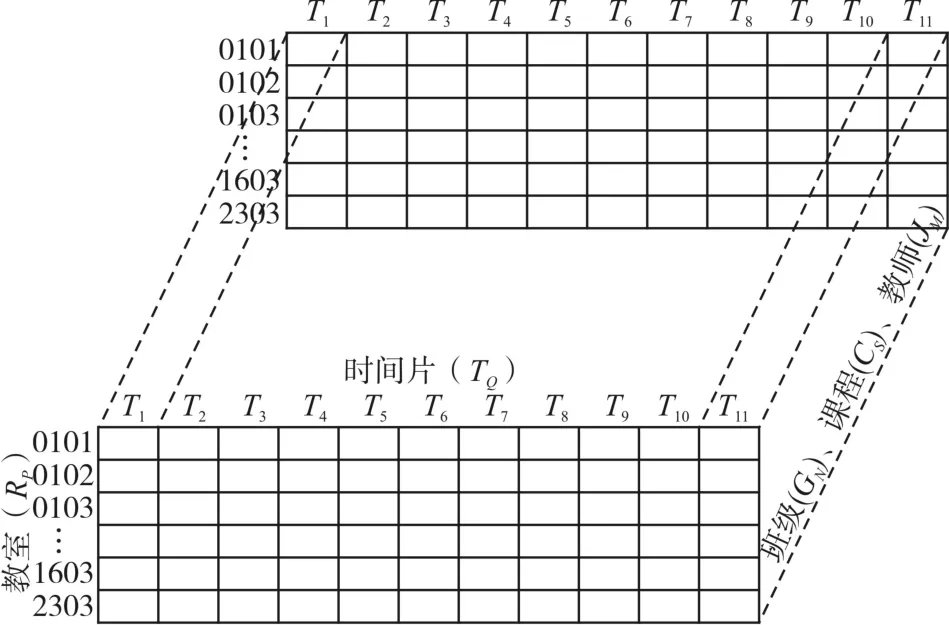
圖2 圖形化編碼方案

具體的染色體編碼設計采用十進制編碼。三位數組中的各數組元素按照表5、表6所示的時間模式編碼表、教室編碼表和班級編碼表，分別映射成為十進制數表示相應的排課信息。

1）時間模式編碼表及含義

表5 時間模式編碼表

模式編碼表中的星期一至星期日分別用十進制數1～7表示；每天有3個教學時間段，分別用1～3表示。考慮到開放教育教學安排的特殊性及多學時課程的教學特點，實際時間段的編碼再添加4位數字位，共6位十進制數表示某課程的教學時間段，并能夠從該編碼中直接獲取該課程的學時數。例如：編碼430000表示該課程在每周四晚上上課；編碼235300表示該課程每周二晚上和周五晚上上課；編碼136273表示該課程每周一晚上、周六下午和周日晚上上課。

2）教室編碼表及含義

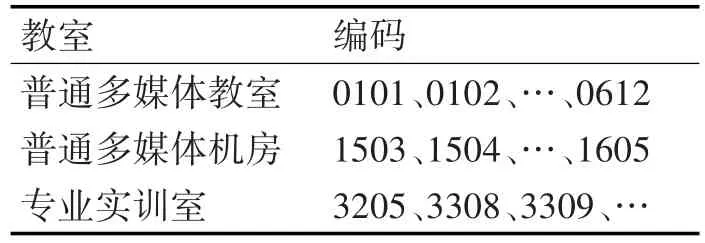
表6 教室編碼表

教室編碼第1位用來區分教室類型，“0”表示普通教室，“1”表示多媒體機房，“2”表示專業實訓室；第2～3位為教室按照樓層的流水號。因為學校僅有一幢教學樓，所以教室編碼不涉及跨區域教室。

3）班級編碼

開放教育實行春、秋兩季本、專科同時招生。按照學校開放教育的實際情況，以專業作為劃分班級的最基本單位。班級編碼由“入學年度”、“專業代碼”、“區分位”三個標識位組合而成。例如：編碼201520111表示2015級工商企業管理專科；具體各專業代碼可提前進行預編碼處理。

2.2 適應度函數設計

適應度函數應滿足規范性、單值、連續，計算簡單，通用性較好等特性。分析可知，適應度函數值是非負的，任何情況下越大越好。目標函數O(x)與適應度函數值Fit(x)之間的關系存在映射問題，即當求O(x)最大值點時，O(x)與Fit(x)的變化方向相同；當求O(x)最小值點時，O(x)與Fit(x)的變化方向相反，此時目標函數值越小，適應度函數值則越大。排課問題的求解依賴于多目標優化，即滿足多個硬約束條件與盡量多的軟約束條件，達到資源分配的最優化。本文提出加權約束適應度函數模型，即：

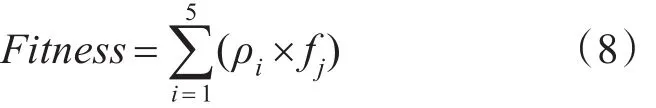
2.3 初始化種群

算法初始化為后續選擇算子、交叉算子、變異算子提供基礎染色體群。經典的遺傳算法通過隨機搜索的方式［12］產生初始種群。這些隨機產生的初始種群在可行解空間上會出現較均勻的散步與較集中的聚集兩種極端情況。

1）隨機搜索法

本文通過一維多峰函數對初始種群的隨機搜索方式進行測試，進一步說明這種由隨機搜索方式產生的初始化種群對遺傳算法的影響。

例如一維多峰函數

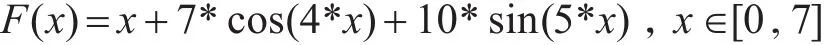
在解的表示方式、初始種群規模、算子、算法終止條件等算法控制參數相同的情況下求解該函數的最大值，以此觀察隨機搜索產生的初始化種群對遺傳算法的計算結果的影響。通過Matlab求解得到圖3計算結果。

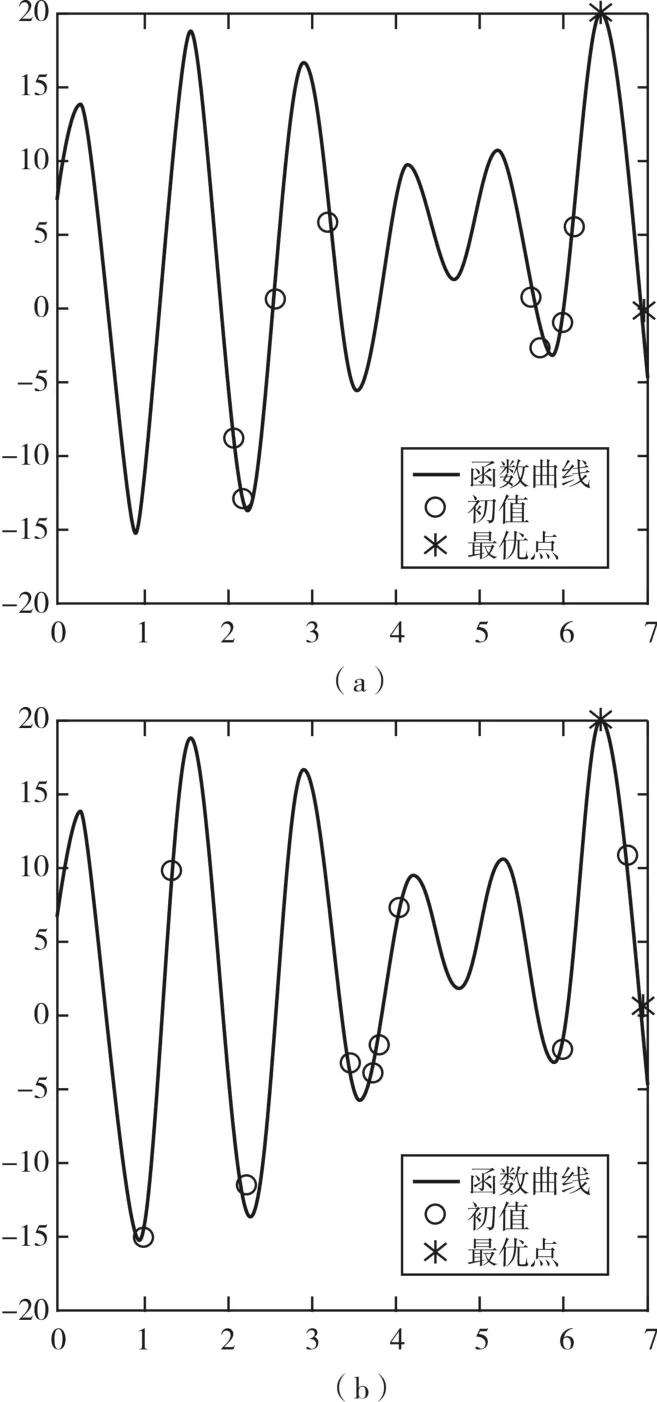
圖3 一維多峰函數測試結果

圖3 （a）、（b）分別為采用同一隨機搜索方式產生經過20次迭代產生初始化種群的遺傳算法程序計算結果。圖3（b）顯示，經過種群迭代，隨機搜索方式產生的個體呈現小范圍集聚，且略微偏向左側，導致算法計算結果較早收斂，形成局部最優。分析可知，在遺傳算法的遺傳代數與算子一定的情況下隨機搜索方式產生的初始種群會引起遺傳算法的不穩定的計算結果。

2）可行解空間網格劃分法

隨機搜索法產生的初始化種群在均勻散步的狀態下具有較高的多樣性，經過遺傳算子操作收斂于全局最優解可能性較大；但同時，隨機搜索產生的分布集中的初始種群會較集中地落在某些子空間中，從而導致遺傳操作收斂到子空間的局部最優解，算法搜索產生停滯，搜索空間無法擴大，算法無法收斂到最優解［11］。由于隨機搜索法產生的種群適應度較低，且具有不穩定性質。為了能夠提高初始種群的群體適應度，本文運用空間網格劃分法產生初始化種群。具體步驟如下：

步驟1：將目標空間進行網格化劃分。參考點落入可行解空間的所有網格，且將每個網格作為一個參考對象。根據種群的規模控制參考點的數量，通過參考點的組合求解多目標優化的可行解。

步驟2：在可行解空間，將m維向量構成的目標空間劃分為k等份。這樣得到m*k個目標子空間，k的值根據計算精度要求與可行解空間的大小進行設定。m*k個目標子空間對應k?m可行解子空間，產生k?m個網格。

步驟3：將每個網格映射為個體目標函數值，可以得到初始種群數為k?m。

步驟4：設某個體目標函數的解空間為[Xmin，Xmax]，依二分法求均值的思路，在解空間搜索i個點，則目標函數值為

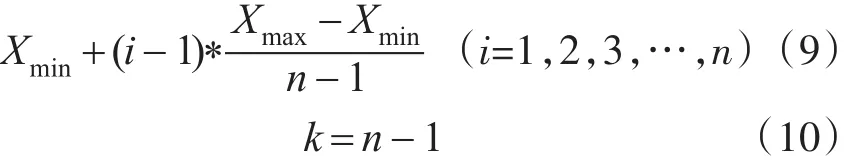
通過解空間網格化劃分產生的初始點，包括全局最優點與局部最優點必然全部落在網格節點或者節點之間，種群進化搜索過程中，算法能夠被較容易地搜索到最優點。這種方法產生的初始種群包含最優解組合的概率明顯增強，且技術性地避免了相似個體的被選取，以減少種群數量。該方法與算法的選擇、交叉、變異算子結合，可以提高算法搜索效率與收斂于全局最優解的概率。

2.4 選擇、交叉、變異操作

經典遺傳算法的選擇策略是基于個體適應度的比例擇優選擇策略。設計的選擇算子不同將導致個體不同的選擇概率，從而產生的種群亦有不同。傳統選擇排序算子的概率值依據經驗設定，適應度概率較高的個體會以較高的概率進化到下一代種群當中，但同樣也存在被淘汰的情況；輪盤選擇方法則無法處理個體適應度值非負數的情況，通用性較差。而在排序選擇方法中，概率分布無規律可循，容易引起局部收斂［13］，造成算法搜索緩慢的問題。

2.4.1 正弦選擇算子

本文提出一種基于最優個體保留策略的正弦函數選擇算子，可以有效提高算法的搜索精度。改進的選擇算子選擇策略分兩步進行。

步驟1：基于個體適應度值，將當前代種群中適應度最高的個體直接復制到下一代。假設第k代最優個體為 Amax(k)，第 k+1代最劣個體Amin(k+1)。保留Amax(k)，并直接替換Amin(k+1)，Amax(k)不參與交叉、變異遺傳操作。第k+1代的種群數為

SA(k+1)=SA(k+1)+Amax(k)-Amin(k+1)

步驟2：對當前代（第k代）種群的其它個體采用改進的正弦函數選擇算子進行選擇與復制操作 。 根 據 正 弦 函 數 f(θi)=sin(θi) 的 特 性 ，當θ ∈[0，π]，f(θ)在 [0，1]區間呈現單調遞增。假設種群個體的適應值為 f1，f2，…，fn，fi∈[fmin，fmax]，i=1，2，...n 。 將 fi∈[fmin，fmax] 等 比 例 映 射 到θ∈[0，]，則可以設計選擇概率：

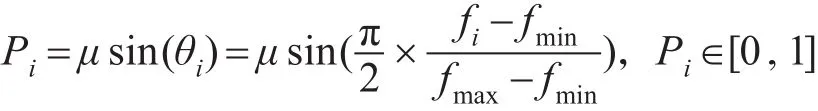
μ為比例調節系數，作用是保證選擇概率在［0，1］區間內均勻分布，降低產生偏差的幾率。

步驟3：結合輪盤賭選擇方法進行選擇運算。

2.4.2 自適應交叉算子［14］

經典遺傳算法會由于進化過程中交叉概率Pc和變異概率Pm保持不變導致算法性能的下降。依據經驗知識與算法規則可知，在種群迭代初期，設置較大的交叉概率能夠明顯增強算法的搜索能力；在種群迭代后期，交叉概率設定小一點則可以有效避免優良基因被淘汰，從而加快算法的收斂［15］。為了提高算法的性能，降低最優個體（適應度高）被淘汰的幾率，本文應用最優個體保留策略，最優個體被保留，不參與交叉和變異操作，剩余個體參與交叉和變異操作，防止陷于局部最優。采用自適應交叉概率為

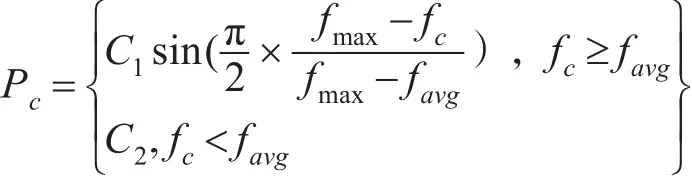
其中，C1為調解系數，其值為（0，1）的隨機數，通過在計算機程序中設置rand隨機函數產生；C2為（0，1）之間的常量；fmax表示種群當前代t中的最優個體適應度函數值；favg表示t中個體的平均適應度函數值；fc表示經過交叉操作的個體中適應度函數值的最大值。

2.4.3 自適應變異算子［14］

種群個體具備的基因差異性對于整個種群的進化的起著至關重要的作用。優良個體之間的基因基因重組可以保證進化過程中種群的優良基因被保留下來，基因較差的個體則會被淘汰，這就是優勝劣汰的選擇過程。可以對種群中不同個體設定不同的變異概率。對于種群中的優良個體，設定較小的變異概率，從而保證優良個體通過交叉操作后能夠，優良基因被保存和累積；對于種群中的較差個體，設定較大的變異概率，通過交叉操作增強種群的搜索能力［16］。基于上述分析，算法的變異操作采用自適應變異概率以提高種群的多樣性，增強算法維持搜索的能力。在種群迭代初期，自適應概率能夠在個體性能較差的條件下，造成較大的擾動來擴大算法的解空間；隨著迭代次數的增加，自適應變異概率能夠逐步減少成為一個0～1之間的常量，以保證算法的平滑收斂。采用自適應變異概率為

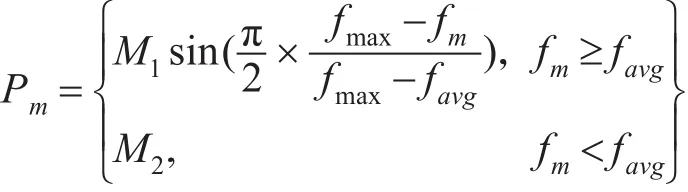
其中，M1為調解系數，其值為（0，1）的隨機數，通過在計算機程序中設置rand隨機函數產生；M2為（0，1）之間的常量；fmax、favg含義同上；fm表示經過交叉操作的個體中適應度函數值的最大值。

3 仿真實驗

課程編排可以歸結為教學資源分配的數學問題［17～18］。排課問題被證明是一種NP問題［19］。遺傳算法的整體搜索策略與求解優化設計對求解問題類型具有較強魯棒性，即算法本身的搜索策略與求解優化技術不依賴于具體求解問題所涉及的領域知識［20］，僅在算法進化過程中，對問題的目標函數求解方向與適應度函數有所影響。本文以某開放大學2015年秋季的排課數據作為算法訓練樣本求解排課問題。數據集如表7所示。

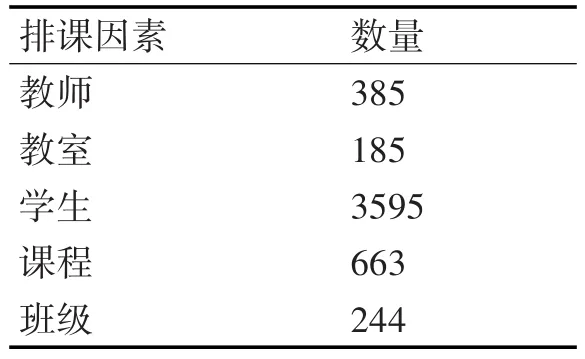
表7 訓練數據集

3.1 Matlab仿真參數設置

本文利用Matlab遺傳算法工具箱，編寫仿真程序對表7數據集進行訓練。在提出的改進遺傳算法中，交叉概率Pc與變異概率Pm具有自適應性，故無需設置。其他參數設置如下：

1）仿真實驗中，種群規模過小會導致目標函數值產生較大的波動；種群過大則可能造成收斂時間較多，消耗資源。NIND表示種群規模，本文設置為200。

2）MAXGEN表示最大遺傳代數，該參數過大會導致過早收斂，無法搜索到全局最優解。根據訓練樣本的數量，本文設置為800。

3.2 Matlab仿真結果

算法仿真實驗中，利用本文提出的空間編碼與正弦選擇算子遺傳算法（SCSS）與Pillay N等［21］提出的改進遺傳算法進行適應度函數值對比。

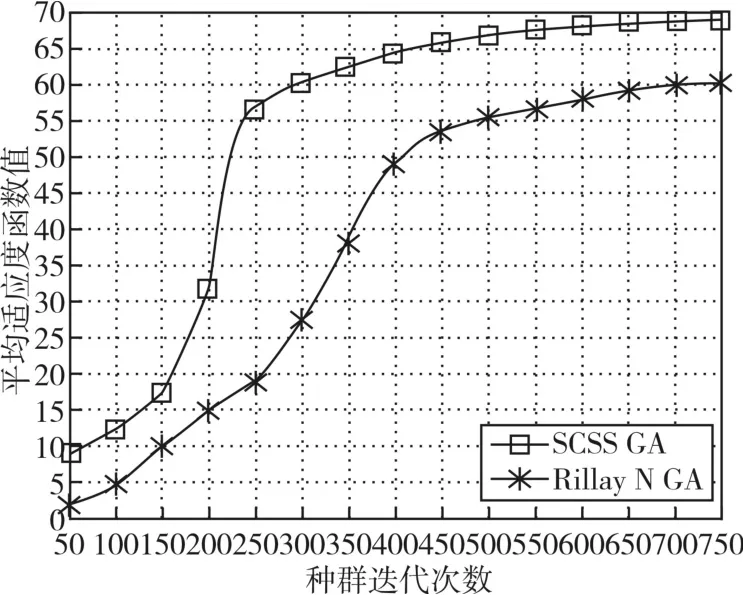
圖4 兩種遺傳算法適應度函數值對比

實驗中，種群每迭代50代就記錄一次種群適應度函數值，共記錄15次。通過計算15次記錄的最佳適應度函數值的平均值，得出圖4所示的實驗結果。從結果可以看出，本文提出的SCSS遺傳算法能夠較好地解決開放教育排課問題。

4 結語

本文提出的基于空間編碼和正弦選擇算子遺傳算法—SCSS，從算法性能和早熟收斂兩個方面對經典遺傳算法進行了改進。基于三維空間染色體編碼可以有效增強種群多樣性。在選擇算子的非線性變換中加入正弦三角函數，改善了算法的收斂性能。通過采用SCSS仿真求解開放教育排課問題，進一步驗證了SSCS遺傳算法具有較好地全局收斂性。

［1］J.H.Holland.Adaptation in natural and artificial systems［M］.Ann Arbor：The University of Michigan Press，1975.08-30.

［2］De Jong，Kenneth Alan.An analysis of the behavior of a class of genetic adaptive systems［D］.Michigan：University of Michigan，1975.05-35.

［3］周明，孫樹棟，等.遺傳算法原理及應用［M］.北京：國防工業出版社，1999.11-13.ZHOU Ming，SUN Shudong，et al.Genetic algorithm：Theory and Application［M］.Beijing：National Defence Industry Press，1999.11-13.

［4］Muehlenbein H.How genetic algorithms really work：mutation and hill climbing［C］//In Proc，and Workshop Parallel Problem Solving from Nature，1992：15-25.

［5］劉紅，韋穗.遺傳算子的分析［J］.計算機技術與發展，2006，16（10）：80-82.LIU Hong，WEI Hui.Analysis on Genetic Operators Computer［J］.Technology and Development，2006，16（10）：80-82.

［6］Ichikawa Y，Ishii Y.Retaining diversity of genetic algorithms for multivariable optimization and neural network learning［C］//Proc of IEEE international conference on neural net-work.［s.l.］：［s.n.］，1993：1110-1114.

［7］Srinivas M，Patnaik L M.Adaptive probabilities of crossover and mutation in genetic algorithm［J］.IEEE trans on systems，man and cybernetics，1994，24（4）：656-667.

［8］楊啟文，蔣靜坪，張國宏.遺傳算法優化速度的改進［J］.軟件學報，2001，12（2）：270-275.YANG Qiwen，JIANG Jingping，ZHANG GUOhong.Improved Optimization Speed for Genetic Algorithms［J］.Journal of Software，2001，12（2）：270-275.

［9］鄭生榮，賴家美，劉國亮，等.一種改進的實數編碼混合遺傳算法［J］.計算機應用，2006，26（8）：1959-1962.ZHENG Shengrong，LAI Jiamei，LIU Guoliang，et al.Improved real coded hybrid genetic algorithm［J］.Computer Applications，2006，26（8）：1959-1962.

［10］錢海軍.開放教育排課問題約束分析與數學建模［J］.軟件工程，2016，19（9）：27-29.QIAN Haijun.Constraint Analysis and Mathematical Modeling in the Open Education Timetabling［J］.Software Engineering，2016，19（9）：27-29.

［11］Shi Juan.Research on application of IGA（Immune Genetic Algorithm）to the solution of course-timetabling problem［C］//Proceedings of 2009 4th International Conference on Computer Science and Education，Nanning，China，2009：1105-1109.

［12］Guyon O，Lemaire P，Pinson*.Cut Generation for an Inte-grated Employee Timetabling and Production Scheduling Problem［J］.European Journal of Operational Research，2010，201（2）：557-567.

［13］Pandey H M，Chaudhary A，Mehrotra D.A comparative Review of Approaches to Prevent Premature Convergence in GA［J］.Applied Soft Computing，2001，24：1047-1077.

［14］朱灝東，李紅嬋.采用三維小生境遺傳算法求解高校排課問題［J］.計算機工程與應用，2011，47（34）：242-245.ZHU Haodong，LI Hongchan.Three-dimensional niche GA used to solve University Timetabling Problem［J］.Computer Engineering and Applications，2011，47（34）：242-245.

［15］馬清亮，胡昌華，陳新海.遺傳算法交叉和變異操作的模糊優化［J］.計算機工程與應用，2002，38（19）：33-34.MA Qingliang，HU Changhua，CHEN Xinhai.Fuzzy Optimization of Crossover and Mutation Opertion in Genetic Algorithm［J］.Computer Engineering and Applications，2002，38（19）：33-34.

［16］熊軍，高敦堂，都思丹，等.變異率和種群數目自適應的遺傳算法［J］.東南大學學報（自然科學版），2004（34）：553-556.XIONG Jun，GAO Duntang，DU Sidan，et al.Genetic algorithm with mutation probability and population size adaptation［J］.Journal of Southeast University（Natural Science Edition），2004（34）：553-556.

［17］Adewumi A O，Sawyerr B A，Montaz A M.A Heuristic Solution to the University Timetabling Problem［J］.Engineer-ing Computations，2009，26（8）：972-984.

［18］朱冠宇，王乘，席大春.利用遺傳算法求解中學課表安排問題［J］.計算機工程與應用，2004（27）：215-218.ZHU Guanyu，WANG Cheng，XI Dachun.Genetic Algorithm for Solving Curriculum Schedule Problem of Senior High School［J］.Computer Engineering and Applications，2004（27）：215-218.

［19］Shi Juan.Research on Application of IGA（Immune Genetic Algorithm）to the Solution of Course-Timetabling Problem［C］//MProc of the 4th Int.l Conf on Computer Science and Education，2009：1109-1105.

［20］Detienne B，Péridy L，Pinsoné.Cut generation for an employee timetabling problem［J］.European Journal of Operational Research，2009，197（3）：1178-1184.

［21］Pillay N，Banzhaf W.An Informed Genetic Algorithm for the Examination Timetabling Problem［J］.Applied Soft Computing，2010，10（2）：457-467.

Using a Space Coding and Sine Selection Operator GA to Solve the Timetabling Problem

QIAN Haijun
（Zhuhai City Polytechnic，Zhuhai 519000）

Genetic algorithm（GA）is an effective algorithm to solve multi-constrained and multi-objective combinatorial optimization problems.The classical genetic algorithm has the characteristics of premature convergence，which can lead to the local optimal solution.In order to improve the algorithm global searching performance，the paper proposed the genetic algorithm based on space coding and sine selection operator，or SCSS，taking the two aspects of chromosome coding design and selection operator design for the genetic algorithm as the cut-in point.The simulation results show that the SCSS genetic algorithm can solve the Open Education timetabling problem with multiple constraints，and provides a practical mathematical method to solve the problem of scheduling problem effectively.The improved genetic algorithm can quickly converge to the global optimal solution of the problem，and the global search performance of the algorithm is obviously enhanced.

genetic algorithm，multi-constrained，space coding，sine selection operator，the Open Education，the global optimal solution

TP301.6

10.3969/j.issn.1672-9722.2017.10.008

Class Number TP301.6

2017年4月17日，

2017年5月28日

2015年度廣東省教育信息技術研究“粵教云”計劃專項重點課題《基于興趣簇的云流媒體系統模型的研究》（編號：2015YJYZ016）；2014年度廣東遠程開放教育科研基金項目《大數據視角下電大開放教育數據挖掘與分析對教與學的促進研究》（編號：YJ1418）資助。

錢海軍，男，碩士，副教授，研究方向：系統理論，數據挖掘。