安全多方空間兩平行直線間距離計算*

于金霞，趙翠平，張 靜,2，湯永利+

1.河南理工大學 計算機科學與技術學院，河南 焦作 454000

2.北京交通大學 計算機與信息技術學院，北京 100044

安全多方空間兩平行直線間距離計算*

于金霞1，趙翠平1，張 靜1,2，湯永利1+

1.河南理工大學 計算機科學與技術學院，河南 焦作 454000

2.北京交通大學 計算機與信息技術學院，北京 100044

為提高三維空間兩平行直線間距離協議的計算效率，基于安全兩實數和平方（secure square of two real numbers sum，SSTS）計算協議與Paillier同態加密算法（Paillier homomorphic encryption algorithm，PHEA）分別提出了三維空間兩平行直線間的距離計算協議。SSTS協議利用空間任一點到直線的距離推導出三維空間兩平行直線間的距離，通過安全兩實數和平方計算協議構造輔助數據來隱藏自己的具體數據；PHEA協議通過Paillier同態加密算法將自己直線方程的系數隱藏，能與對方進行交流計算，但不會泄露自己的具體數據；兩個協議均能保密地計算出三維空間兩平行直線間的距離。分別證明了兩個協議的正確性，并利用模擬范例證明了兩個協議的安全性。最后，對SSTS協議和PHEA協議與現有協議進行比較分析，結果表明，新協議有較低的計算復雜性和通信復雜性，比現有協議至少降低了50%。

隱私保護的計算幾何；空間距離；安全兩實數和平方；同態加密；模擬范例

1 引言

隨著互聯網的快速發展，陌生用戶之間的合作計算變得越來越重要，企業和組織機構既要在合作計算交流信息的過程中保密自己的有價值數據，又要通過整合資源獲得利益，在此背景下安全多方計算應運而生。安全多方計算最初是圖靈獎獲得者Yao[1]提出的，經過了Goldreich等人的發展[2]，逐漸成為現代密碼學及電子商務等眾多應用領域的重要研究課題之一。安全多方計算（secure multi-party computation，SMC）是信息社會隱私數據保護的核心技術，是指兩個或多個參與者在不泄露各自輸入的隱私數據情況下，能夠利用這些隱私數據參加保密計算，共同完成某項計算任務。安全多方計算在大數據安全與隱私保護[3-6]、基因序列[7-9]、數據挖掘[10]、密鑰分配、科學計算等方面得到應用廣泛。

基于隱私保護的計算幾何是安全多方計算領域重要研究內容之一，在商業、軍事和保密圖像處理等方面擁有廣泛的應用前景[11]和潛在的應用價值。目前已經有一些重要的研究成果：在平面幾何方面，Du等人[12]利用置換協議和安全兩方點積協議不僅提出了平面上兩條直線的相交判定問題和凸包的相交問題，而且給出了解決此類問題有用的知識模塊，但是函數求值時可能產生信息泄露。文獻[13]針對Du的算法進行了修改，但當用戶輸入的隱私數據需要保護時，對傳統算法做簡單改進也不能滿足要求，對此提出半誠實模型下計算幾何中關于線段最核心的算法——叉積協議，此協議不僅可以用于解決保護私有信息的計算幾何問題，而且可以用于解決秘密比較等一般的安全多方計算問題，但對方可以惡意輸入虛假數據或者隨意終止協議運行。文獻[14]針對Du的兩線段相交計算復雜性高的問題提出一種高效的不經意傳輸協議，并將高效不經意傳輸協議擴展到判定兩個任意多邊形和兩個任意幾何圖形相交問題。文獻[15-18]研究了點包含問題，文獻[15]中的協議只使用于一些簡單多邊形域，文獻[16]中的協議只使用于圓域，文獻[17]研究了點與橢圓之間的關系，文獻[18]研究了點是否在一個凸多邊形內。由于文獻[15-18]都具有局限性，文獻[19]基于角旋轉法提出了保護隱私的任意多邊形點包含兩方計算協議，并給出正確性和安全性證明，但此協議計算效率低。文獻[20]所提協議不僅可以判定點與任意多邊形的包含問題，而且比現有協議更加高效和安全，但是基于半誠實模型的，是不切實際的。文獻[15-18]研究的都是點包含問題，但在實際應用中具有局限性。文獻[21]研究了點與曲線關系的隱私保護協議，解決了在不泄露任何信息的情況下和在不同情形下如何確定點與曲線位置關系的問題。文獻[22]研究了安全兩方圓計算協議，并利用這些協議解決了保護私有信息的圓與圓的位置關系和圓與直線的位置關系判定問題。以上研究僅局限于平面對象，對更為復雜的空間問題并未涉及。文獻[23]對平面線段相交問題進行了研究和擴展，利用點積協議和比較相等協議設計了保護私有信息的對應成比例判定協議，解決了空間幾何對象相對位置判定問題，但此協議是在兩方安全環境下提出的，具有較高的計算復雜度；多數保護私有信息的幾何對象相對位置協議側重于定性研究，文獻[24]則定量對線、面之間的角度及線線之間的距離問題進行更深入的研究，構建出三維空間線、面夾角協議和線、線距離協議，有效降低了計算復雜度，并且可用于解決更多的其他計算幾何問題，但協議是基于半誠實模型的，在惡意模型下對這些問題的協議分析和設計都非常復雜。文獻[11]研究了空間幾何中四面體的體積、點到平面的距離、直線與平面關系和兩平面關系的多方安全問題及其應用，并利用模擬范例證明協議是安全的，但仍有許多計算幾何問題需要研究。文獻[25]研究了空間兩平行直線間的距離問題，但計算復雜度和通信復雜度很高。

本文針對三維空間兩平行直線間的距離問題提出了兩個新的安全計算協議：SSTS（secure square of two real numbers sum）協議基于安全兩實數和平方協議的方法解決了空間兩平行直線間距離問題的安全多方計算，PHEA（Paillier homomorphic encryption algorithm）協議基于Paillier的同態加密算法高效解決了空間兩平行直線間距離問題的安全多方計算。經過理論分析，SSTS協議在計算復雜度和通信復雜度上比現有解決方案的復雜度至少降低了50%，并證明了其正確性和安全性。在SSTS協議的基礎上，進一步提出了更加安全高效的解決方案——PHEA協議。

2 預備知識

2.1 安全兩實數和平方計算協議

協議1安全兩實數和平方計算[22]。

Alice和Bob各有1個實數n1和n2,Alice和Bob希望在不泄露各自的私有輸入信息時，保密地計算(n1+n2)2。經計算，Alice得到r1,Bob 得到r2,使得r1+r2=(n1+n2)2。

步驟2 Alice和Bob利用退化的一維安全兩方點積協議計算n1?n2：Alice得到R1，Bob 得到R2，使得R1+R2=n1?n2。

2.2 同態加密方案

同態加密方案[26]在云計算和安全多方計算中發揮著不可替代的作用，是公鑰加密方案中的一種。同態加密的特質可以采用對密文進行運算代替對明文的某些運算并取得同樣的效果，而不影響明文數據的保密性。本文運用的是Paillier加密方案[27]的加法同態Ek(x)·Ek(y)=Ek(x+y),從加法同態性的性質得E(x)m=E(mx)。

2.3 Paillier加密方案

密鑰產生：

（1）隨機選取兩個素數p和q，且滿足gcd(pq,(p-1)(q-1))=1。

（2）計算n=pq和λ=lcm(p-1,q-1)。

加密/解密：

對于明文m(m∈Zn)，選擇隨機數r(r∈Z?n)。

加密，c=gmrnmodn2。

解密，m=L(cλmodn2)umodn。

2.4 安全性

假設Alice與Bob都是半誠實的參與者，Alice擁有私有數據x，Bob擁有私有數據y，他們希望合作計算函數F∶(x,y)→ ( )f1(x,y),f2(x,y)而不泄露各自擁有的私有數據x和y。即Alice與Bob保證各自提供私有數據真實的前提下，嚴格按照協議的流程執行，不會中途退出或更改協議執行的步驟，但有可能會保留中間過程產生的結果用于推算對方的隱私數據。設P為計算函數F的協議，當輸入為(x,y)時,記為Alice（Bob）在執行協議P的過程中所得到的消息序列，是,其中r1(r2)表示Alice（Bob）獨立的硬幣拋投結果；表示Alice（Bob）第i次收到的信息。記為Alice（Bob）得到的輸出結果。

定義1（半誠實參與者的保密性[28]）對于一個函數F，如果存在概率多項式時間算法S1與S2（也稱這樣的多項式時間算法為模擬器）使得：

則稱P保密地計算函數F（其中表示計算上不可區分）。

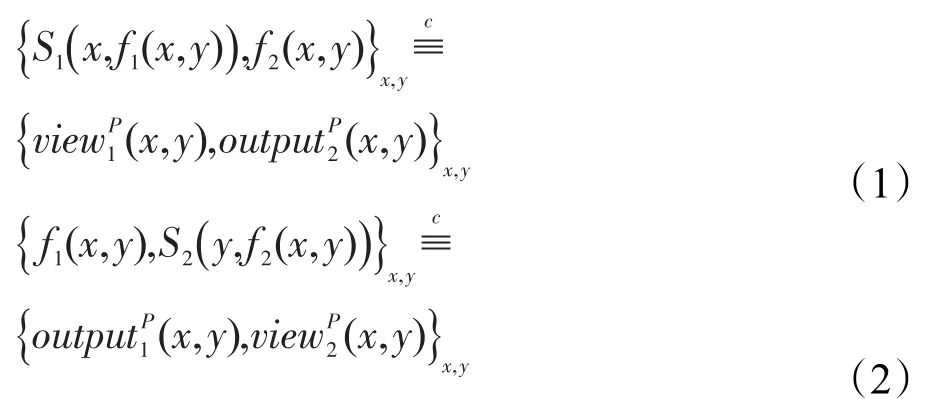
3 安全多方計算方案

3.1 空間兩平行直線間距離問題的解決方案1

文獻[25]雖然解決了空間兩條平行直線間的距離問題，但是因為利用不經意傳輸協議，其計算復雜度和通信復雜度很高。本文根據幾何學知識和安全兩實數和平方計算協議理論提出了三維空間兩平行直線間的距離計算協議。首先，該協議是針對三維空間兩平行直線的標準式提出的；然后，根據三維空間點到直線的距離推導出三維空間兩條平行直線間的距離；最后，通過安全兩實數和平方協議計算出輔助數據，使Alice和Bob只知道他們隱私數據和的平方值，但永遠不可能知道對方數據的具體值。此協議在通信安全保密中的優勢：文獻[25]空間兩平行直線間距離的保密計算協議共調用6次不經意傳輸協議和6次點積協議，本文中SSTS協議只調用3次點積協議。文獻[25]計算復雜度是12(m+1)lgk,而SSTS協議的計算復雜度是6mlgk；文獻[25]通信復雜度是6(m+1)，而SSTS協議的通信復雜度是3m+1。總之，在計算復雜度和通信復雜度上，SSTS協議比文獻[25]至少降低了50%。由于SSTS協議使用了安全兩實數和平方計算協議，即點積協議，本協議的安全性主要依賴于點積協議。對于點積協議，在輸入階段，Alice和Bob分別通過隨機值來掩蓋其隱私向量；協議執行后，Alice和Bob都只能獲得點積的計算值而無法得知對方的向量值。

假設空間有一點P1(x1,y1,z1)和一條直線，取直線t2上的一點M0(x2,y2,z2)，設M0P1與直線t2方向向量e=ai+bj+ck所成夾角為θ，則P1到直線e(t2)的距離應為。如圖1所示，,則：

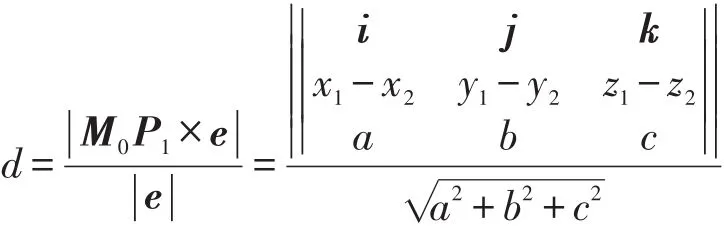
最外面“||”表示矢量取模。

對于三維空間兩平行直線t1、t2，取t1上點P1(x1,y1,z1)，P1到t2的距離即為三維空間兩條平行直線間的距離。

方案的主要思想是基于點到直線的距離保密地推導出三維空間兩條平行直線間的距離。假設Alice擁有一條保密直線t1，在t1上選擇一個保密的點P1(x1,y1,z1)，Bob擁有一條保密直線t2，他們分別利用安全兩實數和平方計算協議計算輔助數據，最后計算出三維空間兩條平行直線間的距離d。

協議2保密地計算出空間兩平行直線間的距離（此協議記為SSTS協議）。

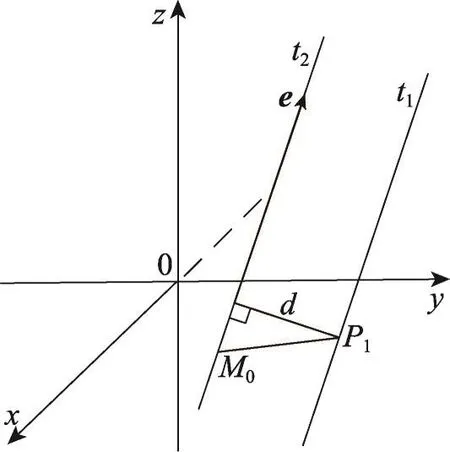
Fig.1 Distance of pointP1to straight linet2圖1 點P1到直線t2的距離

輸出：Alice與Bob合作計算t1和t2間的距離d。

步驟1 Alice在t1上選擇一個保密的點P1(x1,y1,z1)，并計算(y1c-z1b)，Bob在t2上選擇一個保密的點P2(x2,y2,z2)，并計算(z2b-y2c)；Alice與Bob分別利用安全兩實數(y1c-z1b),(z2b-y2c)和平方計算協議，保密計算[(y1c-z1b)+(z2b-y2c)]2；經計算，Alice得到，Bob得到，使得。

步驟2 Alice計算(z1a-x1c),Bob計算(x2c-z2a);Alice與Bob分別利用安全兩實數(z1a-x1c),(x2c-z2a)和平方計算協議，保密計算；經計算，Alice得到，Bob得到，滿足。

步驟3 Alice計算(x1b-y1a)，Bob計算(y2a-x2b);Alice與Bob分別利用安全兩實數(x1b-y1a),(y2a-x2b)和平方計算協議，保密計算；經計算，Alice得到，Bob得到，滿足。

步驟5 Bob計算F,并將F發送給Alice。

定理1 SSTS協議能正確計算出三維空間兩平行直線間的距離。

本文根據SSTS協議的具體驗算過程如下。

Alice和Bob合作計算后得到的信息分別為Alice：。

Alice計算：

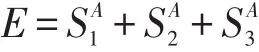
Bob計算：

Alice收到Bob的信息，計算：

Alice計算得到d，但Alice無法從d這個式子中得到關于Bob的任何信息。整個過程中沒有泄露任何信息，并且完成了三維空間兩平行直線間的距離計算，正確性得以證明。

定理2 SSTS協議能安全計算出三維空間兩平行直線間的距離。

在SSTS協議中，首先假定參與的兩方Alice和Bob是半誠實的，在協議執行后，Alice和Bob都只能獲得自己輔助數據的值，無法得知對方的具體值。

在輸入階段，Alice的輸入為保密直線l1，Bob的輸入為保密直線l2。步驟1～步驟3，Alice和Bob先分別選擇自己直線上一個保密的點；然后，分別計算出自己數據的值；最后，分別利用安全兩實數和平方計算協議得到各自輔助數據的值。但Alice無法從中得到Bob值，Bob也無法從中得到Alice的值。步驟4，Alice對自己得到的輔助數據進行計算。步驟5，Bob也對自己得到的輔助數據進行計算，并將計算結果發送給Alice。步驟6，Alice收到Bob的信息后，計算得到M=E+F,E+F是Alice與Bob輔助數據的總和。總之，SSTS協議每一步都是隱私保護的，下面利用模擬器進行具體證明。

證明 通過構造出使式（1）和（2）成立的模擬器S1和S2來證明其安全性。

（1）首先構造模擬器S1使得式（1）成立。在SSTS協議中,其中t1、t2分別是Alice與Bob的輸入。

S1的模擬過程如下：

步驟1S1接受( )t1,f1(t1,t2)作為Alice的輸入，根據f1(t1,t2)的值，任意選定直線t2′，滿足f1(t1,t2′)=f1(t1,t2)，記。

S1利用安全兩實數和平方計算協議分別計算出的值。

步驟2S1根據的值計算出,進而計算出M′=E+F′。根據構造過程知道f1(t1,t2′)=f1(t1,t2)。

步驟3S1根據M′、G的值，計算出。

因為

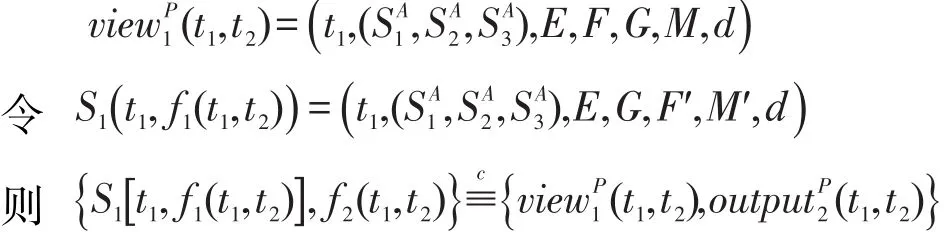
（2）類似地，還可以構造S2使下式成立：

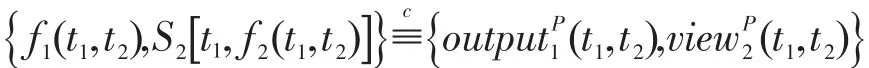
根據定義1可知此協議是安全的。 □

3.2 空間兩平行直線間距離問題的解決方案2

SSTS協議解決了空間兩條平行直線標準式的距離問題。現在研究空間兩條平行直線交面式距離問題的解決方案，Alice擁有一條保密直線L1，Bob擁有一條保密直線L2,Alice與Bob希望在不泄露自己直線方程系數的情況下，保密計算出空間兩平行線間的距離d。該方案的思想是基于Paillier同態加密方案提出了三維空間兩平行直線間的距離計算協議。首先，該協議是針對三維空間兩平行直線的交面式提出的；然后，利用Paillier同態加密方案將Alice直線方程的系數進行加密后發送給Bob，Bob利用Paillier同態加密方案進行計算后發送給Alice；最后，Alice和Bob合作計算出三維空間兩平行直線間的距離。此協議在通信安全保密中的優勢：由3.1節可知文獻[25]計算復雜度是12(m+1)lgk，大約進行180次模指數運算，SSTS協議的計算復雜度是6mlgk，大約進行90次模指數運算；Pailler一次加密需要2次模指數運算，一次解密需要1次模指數運算，而PHEA協議共進行25次模指數運算。由3.1節可知文獻[25]通信復雜度是6(m+1)，SSTS協議的通信復雜度是3m+1；而PHEA協議中通信輪數為3。總之，在計算復雜度和通信復雜度上，PHEA協議效率最優。PHEA協議主要利用了Paillier同態加密算法：（1）同態加密的特質可以用對密文進行運算代替對明文的某些運算并取得同樣的效果，而不影響明文數據的保密性。（2）Paillier同態加密算法是基于計算和判斷上的n次剩余問題的困難性，并給出了一種能夠驗證消息完整性的加密算法，在隨機預言模型下證明了該加密算法能夠抵抗適應性攻擊。

協議3保密地計算空間兩平行直線間的距離（此協議記為PHEA協議）。

輸出：Alice與Bob合作計算L1和L2間的距離d。

步驟1設(G,E,D)是Paillier同態加密方案，k是設定的安全參數，Alice運行G(k)生成同態加密的公鑰和私鑰，Alice向Bob公布生成的公鑰。

步驟2 Alice計算M1=(a1b2+a2b1),M2=(a1c2+a2c1),M3=(a1d2+a2d1),M4=2b1b2,M5=(b1c2+b2c1),M6=(b1d2+b2d1),M7=2c1c2,M8=(c1d2+c2d1),M9=(b1c2-b2c1)2+(c1a2-c2a1)2+(a1b2-a2b1)2，對Mi(i=1,2,…,8)用公鑰進行加密，E(L)=E(Mi)，并將E(L)發送給Bob。

步驟3 Bob計算N1=(c3d4-c4d3),N2=(b3d4-b4d3),N3=(b3c4-c3b4),B=1/N23選 取 隨 機 數R1、R2、R3、R4、R5、R6、R7、R8、R9,然后分別利用 Paillier同態加密方案計算出：

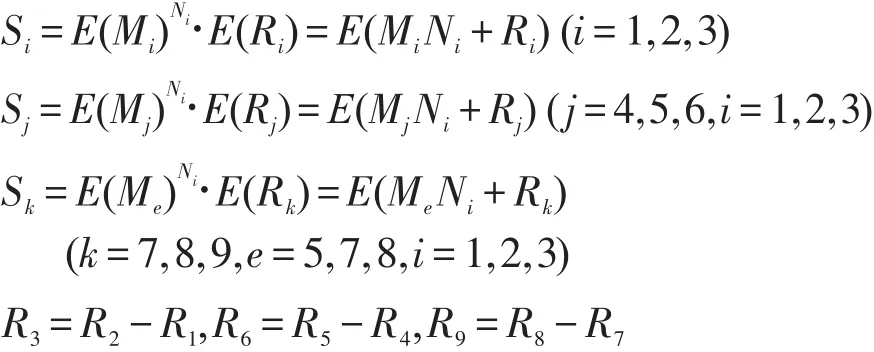
并將B發送給Alice。

步驟4 Alice收到Bob的消息后用私鑰將Wi(i=1,2,…,9)進行解密，并計算出Q1、Q2、Q3。

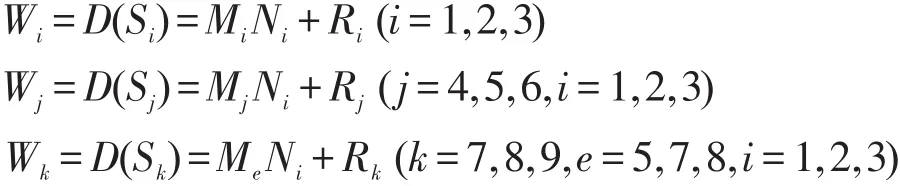
利用解密得到的Wi(i=1,2,3,4,5,6,7,8,9)計算出Qi(i=1,2,3),其中，Q1=(W1-W2+W3)2,Q2=(W4-W5+W6)2,Q3=(W7-W8+W9)2,則,并將A發送給Bob。

定理3 PHEA協議能正確計算出三維空間兩平行直線間的距離。

證明（1）當a1b2-a2b1≠0時，空間兩平行直線間的距離公式：

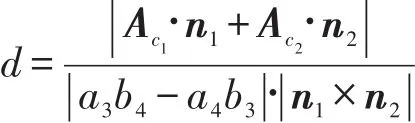
（2）當a2c1-a1c2≠0時，空間兩平行直線間的距離公式：

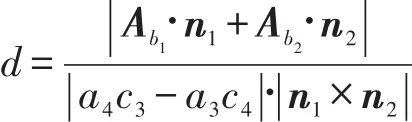
（3）當b1c2-b2c1≠0時，空間兩平行直線間的距離公式：

A的代數余子式：

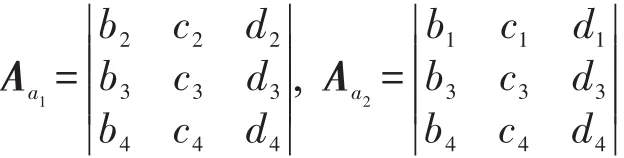
ni是平面πi的法向量。

下面根據PHEA協議以情況（3）為例進行具體驗算。

Alice直線的密文信息：

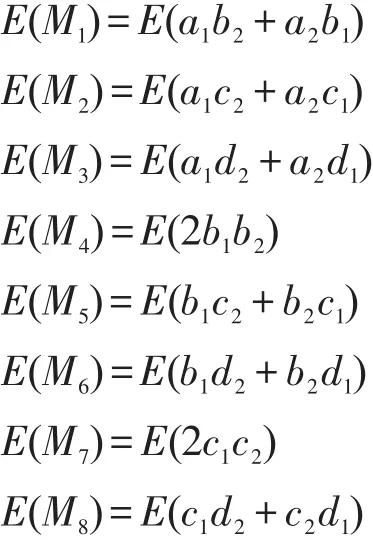
Bob收到Alice的密文信息，計算：

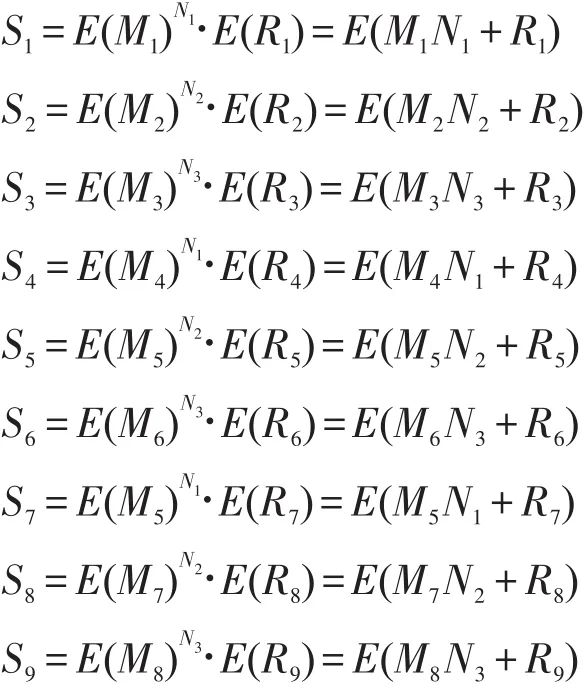
Alice收到Bob的信息后，解密得到：

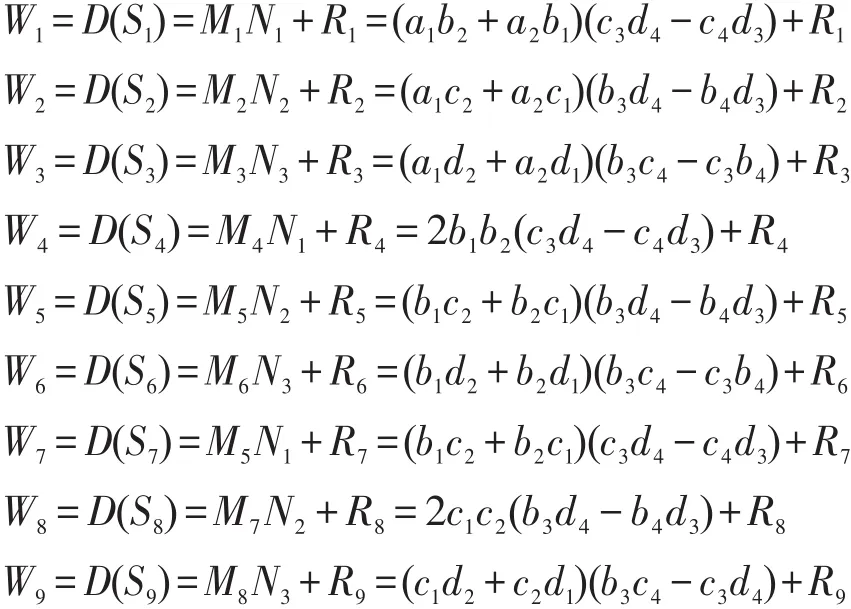
并計算：

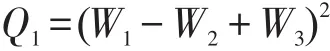
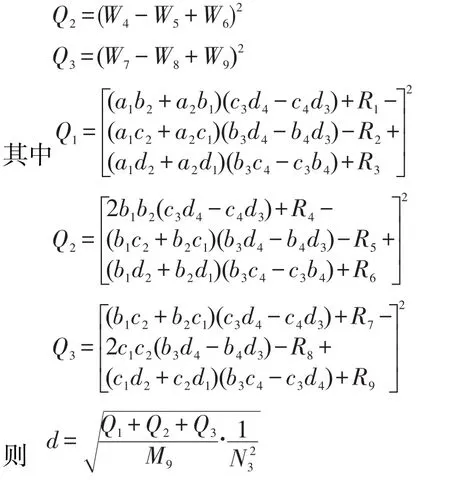
但Alice無法從d這個式子中得到關于Bob的任何信息。整個過程中沒有泄露任何信息，并且完成了三維空間兩平行直線間的距離計算，正確性得以證明。 □

定理4 PHEA協議能安全計算出三維空間兩平行直線間的距離。

為了能夠證明PHEA協議在半誠實模型下的保密性，只需要去驗證協議各方的輸入輸出，然后進行模擬分析。因為在PHEA協議中沒有可信的第三方，所以只需從Alice和Bob的視角來分析其輸入輸出，并作出相應的保密性分析即可。

對于Alice，Alice的輸入為保密直線l1，Alice收到Bob的消息，用私鑰進行解密操作后，Alice得到的是一系列數字，但這些數字中并不包含Bob直線的任何信息值，僅僅是隨機數。因此，從Alice的角度來講滿足隱私性的要求。

對于Bob，Bob的輸入為保密直線l2，Alice對自己的隱私數據用公鑰進行加密后發送給Bob，但Bob并不知道Alice的私鑰，所以Bob無法獲取Alice直線的任何信息。因此，從Bob的角度來講滿足隱私性的要求。

總之，PHEA協議對于Alice和Bob都是隱私保護的，下面利用模擬器進行具體證明。

證明 通過構造出使式（1）和（2）成立的模擬器S1和S2來證明其安全性。

（1）首先構造模擬器S1使得式（1）成立。

在解決方案2中：

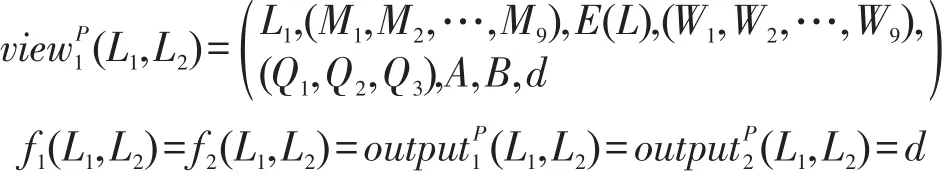
其中，L1、L2分別是Alice與Bob的輸入；E(L)是L的密文。

S1的模擬過程如下：

步驟1S1接受(L1,f1(L1,L2))作為Alice的輸入，根據f1(L1,L2)的值，任意選定直線L2′，滿足

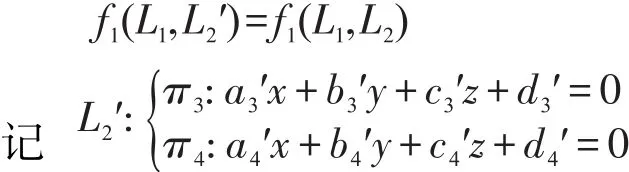
S1分別計算出M1,M2,…,M9,B′的值。

步驟 2S1任意選取 9 個隨機數R1′,R2′,…,R9′，使得R3′=R2′-R1′,R6′=R5′-R4′,R9′=R8′-R7′,用同樣的方法加密Mi(i=1,2,…,8),并且分別計算出W1′,W2′,…,W9′,Q1′,Q2′,Q3′,A′的值。根據構造過程知道f1(L1,L2′)=f1(L1,L2)。

步驟 3S1根據A′、B′的值，計算出d′=A′?B′,則為空間兩條平行直線間的距離。

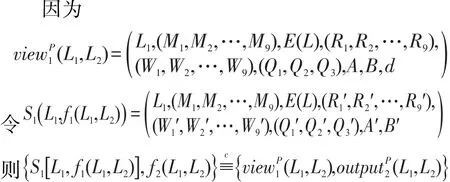
（2）類似地，還可以構造S2使下式成立：

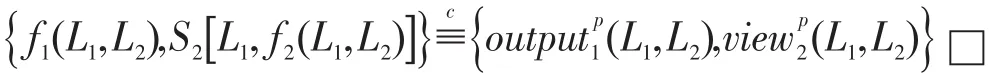
4 復雜性分析

計算復雜性：文獻[25]空間兩平行直線間距離的保密計算協議共調用6次不經意傳輸協議和6次點積協議。本文SSTS協議共調用3次點積協議，PHEA協議進行了8次加密運算，9次解密運算。假設安全參數為m，一次不經意傳輸協議至少需要2lgk次模指數運算，一次點積協議至少需要2mlgk次模指數運算，文獻[25]共需12(m+1)lgk次模指數運算。一般情況下當m＞5,k＞8時才能達到基本的安全級別，故至少需要180次模指數運算。本文SSTS協議至少需要6mlgk次模指數運算，Pailler一次加密需要2次模指數運算，一次解密需要1次模指數運算，PHEA協議共進行25次模指數運算。

通信復雜性：衡量通信復雜性的指標可以采用協議交換的比特數或通信輪數，在安全多方計算研究中通常用通信輪數來衡量計算復雜性。文獻[25]通信輪數為6(m+1)次，本文SSTS協議通信輪數為3m+1次，PHEA協議通信輪數為3。各方案復雜性比較如表1所示。

Table1 Complexity comparison of schemes表1 各方案復雜性比較

因此本文協議計算效率和通信效率更高，適用范圍更廣。

5 結束語

在半誠實模型下，基于安全兩實數和平方計算協議和Paillier同態加密方案分別提出了計算空間兩平行直線間的SSTS和PHEA距離協議，有效降低了計算復雜度和通信復雜度，并且對SSTS和PHEA協議的正確性和安全性分別進行了證明。因為SSTS和PHEA協議都是基于半誠實模型的，當然還有不足之處，在惡意模型下對安全多方空間兩平行直線距離協議進行研究和分析會比較困難，所以未來將繼續對此進行探討并推廣到其他應用領域。

[1]Yao A C C.Protocols for secure computations[C]//Proceedings of the 23rd Annual Symposium on Foundations of Computer Science,Chicago,USA,Nov 3-5,1982.Washington:IEEE Computer Society,1982:160-164.

[2]Goldreich O,Micali S,Wigderson A.How to play ANY mental game[C]//Proceedings of the 19th Annual ACM Symposium on Theory of Computing,New York,May 25-27,1987.New York:ACM,1987:218-229.

[3]Kaushik M,Jain A.Challenges to big data security and privacy[J].International Journal of Computer Science and Information Technologies,2014,5(3):3042-3043.

[4]Bertino E.Big data-security and privacy[C]//proceedings of the 2015 International Congress on Big Data,New York,Jun 27-Jul 2,2015.Washington:IEEE Computer Society,2015:757-761.

[5]Thuraisingham B M.Big data security and privacy[C]//Proceedings of the 5th Conference on Data and Application Security and Privacy,San Antonio,USA,Mar 2-4,2015.New York:ACM,2015:279-280.

[6]Patil H K,Seshadri R.Big data security and privacy issues in healthcare[C]//Proceedings of the 2014 International Congress on Big Data,Anchorage,USA,Jun 27-Jul 2,2014.Washington:IEEE Computer Society,2014:762-765.

[7]Erlich Y,Narayanan A.Routes for breaching and protecting genetic privacy[J].Nature Reviews Genetics,2014,15(6):409-421.

[8]Xie Wei,Kantarcioglu M,Bush W S,et al.SecureMA:protecting participant privacy in genetic association metaanalysis[J].Bioinformatics,2014,30(23):3334-3341.

[9]Sandfuchs B.Privacy nudges:an introduction[M]//Akrivopoulou C M.Protecting the Genetic Self from Biometric Threats:Autonomy,Identity,and Genetic Privacy.Hershey,USA:IGI Global,2015:256-264.

[10]Lindell Y,Pinkas B.Secure multiparty computation for privacy-preserving data mining[J].Journal of Privacy&Confidentiality,2008,25(2):761-766.

[11]Li Shundong,Wu Chunying,Wang Daoshun,et al.Secure multiparty computation of solid geometric problems and their applications[J].Information Sciences,2014,282:401-413.

[12]Du Wenliang,Atallah M J.Privacy-preserving cooperative scientific computations[C]//Proceedings of the 14th Computer Security Foundations Workshop,Cape Breton,Canada,Jun 11-13,2001.Washington:IEEE Computer Society,2001:273-294.

[13]Luo Yonglong,Huang Liusheng,Jing Weiwei,et al.Privacypreserving cross product protocol and its applications[J].Chinese Journal of Computers,2007,30(2):248-254.

[14]Li Shundong,Dai Yiqi,Wang Daoshun,et al.Secure multiparty computations of geometric intersections[J].Journal of Tsinghua University:Science and Technology,2007,47(10):1692-1695.

[15]Atallah M J,Du Wenliang.Secure multi-party computational geometry[C]//LNCS 2125:Proceedings of the 7th International Workshop on Algorithms and Data Structures,Providence,USA,Aug 8-10,2001.Berlin,Heidelberg:Springer,2001:165-179.

[16]Li Shundong,Dai Yiqi.Secure two-party computational geometry[J].Journal of Computer and Technology,2005,20(2):258-263.

[17]Luo Yonglong,Huang Liusheng,Zhong Hong.Secure twoparty point-circle inclusion problem[J].Journal of Computer and Technology,2007,22(1):88-91.

[18]Luo Yonglong,Huang Liusheng.A secure protocol for determining whether a point is insider a convex polygon[J].Chinese Journal of Electronics,2006,15(4):578-582.

[19]Chen Li,Lin Bogang.Privacy-preserving point-inclusion twoparty computation protocol[C]//Proceedings of the 4th International Conference on Computational and Information Sciences,Shiyan,China,Jun 21-23,2013.Washington:IEEE Computer Society,2013:257-260.

[20]Li Shundong,Wang Daoshun,Dai Yiqi.Efficient secure multiparty computational geometry[J].Chinese Journal of Electronics,2010,19(2E):324-328.

[21]Liu Liang,Wu Chunying,Li Shundong.Two privacy-preserving protocols for point-curve Relation[J].Journal of Electronics,2012,29(5):422-430.

[22]Liu Wen,Luo Shoushan,Yang Yixian,et al.A study of secure two-party circle computation problem[J].Journal of Beijing University of Posts and Telecommunications,2009,32(3):32-35.

[23]Luo Yonglong,Huang Liusheng,Jing Weiwei,et al.Privacy protection in the relative position determination for two spatial geometric objects[J].Journal of Computer Research and Development,2006,43(3):410-416.

[24]Zhong Hong,Sun Yanfei,Yan Feifei,et al.Privacy-preserving relative position calculation protocols for spatial geometric objects[J].Journal of Harbin Engineering University,2011,32(4):458-463.

[25]Xin Xin,Hao Lin,Tang Yu.Privacy-preserving computational protocol on minimum distance between two three-dimension parallel straight line[J].Application Research of Computers,2013,30(5):1530-1532.

[26]Frederick R.Core concept:homomorphic encryption[J].Proceedings of the National Academy of Sciences,2015,112(28):8515-8516.

[27]Wu Jiehong,Zhang Po,Shi Xiangbin.Research of MA protection based on addition-multiplication homomorphism and composite function technology[J].Journal of Chinese Computer Systems,2012,33(10):2223-2226.

[28]Reimer B,Fried R,Mehler B,et al.Brief report:examining driving behavior in young adults with high functioning autism spectrum disorders:a pilot study using a driving simulation paradigm[J].Journal of Autism&Developmental Disorders,2013,43(9):2211-2217.

附中文參考文獻：

[13]羅永龍,黃劉生,荊巍巍,等.保護私有信息的叉積協議及其應用[J].計算機學報,2007,30(2):248-254.

[14]李順東,戴一奇,王道順,等.幾何相交問題的多方保密計算[J].清華大學學報:自然科學版,2007,47(10):1692-1695.

[22]劉文,羅守山,楊義先,等.安全兩方圓計算協議[J].北京郵電大學學報,2009,32(3):32-35.

[23]羅永龍,黃劉生,荊巍巍,等.空間幾何對象相對位置判定中的私有信息保護[J].計算機研究與發展,2006,43(3):410-416.

[24]仲紅,孫彥飛,燕飛飛,等.保護私有信息幾何對象的相對位置計算[J].哈爾濱工程大學學報,2011,32(4):458-463.

[25]辛欣,郝林,湯瑜.空間兩平行直線間距離的保密計算協議[J].計算機應用研究,2013,30(5):1530-1532.

[27]吳杰宏,張坡,石祥濱.基于加乘同態與組合函數技術的MA保護研究[J].小型微型計算機系統,2012,33(10):2223-2226.

2016-08,Accepted 2017-01.

Secure Multi-Party Computation on Spatial Distance Between Two Parallel Straight Lines*

YU Jinxia1,ZHAO Cuiping1,ZHANG Jing1,2,TANG Yongli1+
1.College of Computer Science and Technology,Henan Polytechnic University,Jiaozuo,Henan 454000,China
2.School of Computer and Information Technology,Beijing Jiaotong University,Beijing 100044,China
+Corresponding author:E-mail:yltang@hpu.edu.cn

To improve the computational efficiency of the distance between two three-dimension parallel straight lines,this paper proposes two protocols of a secure square of two real numbers sum protocol(SSTS)and Paillier homomorphic encryption algorithm(PHEA).Firstly,SSTS is to derive the distance between two three-dimension parallel straight lines by the distance from a point to a straight line,and it constructs auxiliary data to hide their own specific data by a secure square of two real numbers sum protocol.Secondly,PHEA uses Paillier homomorphic encryption algorithm to hide linear equation coefficient.Parties can communicate with each other,but will not reveal their specific data.Two protocols are confidential to calculate the distance between two three-dimension parallel straight lines.In addition,this paper proves the validity of two protocols,and proves the security by the simulation example.Finally,this paper analyzes the computation complexity and communication complexity of SSTS and PHEA with the existing protocol.The results show that the new protocols are at least 50%less than that of the existing protocol.

privacy-preserving computational geometry;space distance;secure square of two real numbers sum;homomorphic encryption;simulation paradigm

10.3778/j.issn.1673-9418.1608069

*The National Natural Science Foundation of China under Grant No.61300216(國家自然科學基金);the International Science and Technology Cooperation Program of Science and Technology Office of Henan Province under Grant No.152102410048(河南省科技廳國際科技合作計劃);the Research of Basic and Advanced Technology of Henan Province under Grant No.142300410147(河南省基礎與前沿技術研究);the Natural Science Research Project of Education Department of Henan Province under Grant Nos.12A520021,16A520013(河南省教育廳自然科學研究項目).

CNKI網絡優先出版:2017-01-05,http://www.cnki.net/kcms/detail/11.5602.TP.20170105.0828.002.html

YU Jinxia,ZHAO Cuiping,ZHANG Jing,et al.Secure multi-party computation on spatial distance between two parallel straight lines.Journal of Frontiers of Computer Science and Technology,2017,11(11)：1764-1774.

A

TP309

YU Jinxia was born in 1974.She received the Ph.D.degree in artificial intelligence from Central South University in 2007.Now she is a professor at Henan Polytechnic University.Her research interests include artificial intelligence and information security,etc.

于金霞（1974—)，女，河南博愛人，2007年于中南大學獲得博士學位，現為河南理工大學教授，主要研究領域為人工智能，信息安全等。

ZHAO Cuiping was born in 1989.She is an M.S.candidate at Henan Polytechnic University.Her research interests include information security and cryptology,etc.

趙翠平（1989—），女，河南商水人，河南理工大學碩士研究生，主要研究領域為信息安全，密碼學等。

ZHANG Jing was born in 1978.Now she is an associate professor at Henan Polytechnic University.Her research interests include network and information security,secure multi-party computation,etc.

張靜（1978—），女，河南焦作人，河南理工大學計算機科學與技術學院副教授，主要研究領域為網絡與信息安全，安全多方計算等。

TANG Yongli was born in 1972.He received the Ph.D.degree in cryptology from Beijing University of Posts and Telecommunications in 2008.Now he is an associate professor at Henan Polytechnic University.His research interests include information security and cryptology,etc.

湯永利（1972—），男，河南孟州人，2008年于北京郵電大學獲得博士學位，現為河南理工大學副教授，主要研究領域為信息安全，密碼學等。