社會網中時間最優的利潤最大化算法研究*

劉 勇，謝勝男，張 巍，朱敬華，王 楠

黑龍江大學 計算機科學技術學院，哈爾濱 150080

社會網中時間最優的利潤最大化算法研究*

劉 勇+，謝勝男，張 巍，朱敬華，王 楠

黑龍江大學 計算機科學技術學院，哈爾濱 150080

影響最大化問題是在社會網上尋找最具影響力的種集。目前的研究工作忽略了影響傳播最大化和利潤最大化的區別，以及影響范圍會隨著時間的推移趨于平穩。考慮用戶動作日志，提出了基于時間長度的影響力分配模型IVA-T（influence value allocation-T），在此基礎上首次提出了時間最優的利潤最大化問題（time optimal profit maximization，OTPM），并證明了該問題為NP-hard問題。為求解OTPM問題，提出了一個有效的近似算法Profit-Max，并證明了Profit-Max算法的近似比。多個真實數據集上的實驗結果表明，該算法可以有效并高效地解決OTPM問題。

社會網；利潤最大化；動作日志；時間長度

1 引言

最近幾年，一些規模較大的社會網流行起來，如微信、Instagram、微博等。這些網絡將人們以各種方式聯系起來，進行信息交互和資源共享。進一步，使得社會網的研究具有較大意義，可以通過對社會網中用戶之間的聯系，估計影響傳播概率，進行一些新思想或是新商品的傳播。

基于上述思想，Domingos等人[1]在2001年首次提出了病毒性市場營銷這一概念。在社會網中選取k個有影響力的用戶，免費給他們使用待推廣產品，通過社會網中的口碑效應，使最多的用戶接受并購買該產品。2003年，Kempe等人[2]將上述問題形式化為影響最大化問題：給定有向圖G(V,E)，正整數k，選擇一組節點數為k的集合，即為種集，在給定的影響傳播模型下，最終達到最大的影響范圍。文獻[3-7]針對影響最大化問題進行了進一步的研究，對不同應用背景下的影響最大化提出了相應的解決方案。然而，上述文獻的解決方法并沒有考慮以下兩個問題：（1）在求種集的影響范圍時，沒有考慮成本問題；（2）忽略了營銷時間對影響范圍的影響。

在現實應用中，促銷成本一定會隨著時間推移而增加，而種集的影響范圍會變得平穩，以下的實驗證實了這一觀點。在真實數據集Digg上做了如下實驗：利用文獻[8]中的算法選擇具有最大影響力的10個節點組成種集，選擇了長度遞增的7個時間段，用以觀察種集的影響范圍隨時間的變化，實驗結果如表1所示。其中，T表示不同的時間長度，Spread為影響范圍，表示被影響的節點數量。

Table 1 Spread vs different timespan T in Digg dataset表1 在Digg數據集上影響范圍vs不同的時間長度

從表1可以得出結論，影響范圍會隨著時間的推移而逐漸趨于平穩。從中可以得出另一重要結論，對于不同的時間長度，最終選擇的種集也是不一樣，具體實驗結果見5.4節。因此，在市場營銷應用中，選擇最佳的促銷時長及對應的種集可以幫助商家以最小的成本獲得最大的利潤。

現有如下場景：京東商城的一家商店要推廣一個新的商品，現要在整個社會網中進行促銷。這個商家每天都有一定的促銷成本，每件商品都有一定的利潤。由于受影響而購買該商品的用戶總量會隨著時間的推移而不再呈上升趨勢，所以這家商店期望可以選擇具有較大影響力的用戶和最佳的促銷時間段來獲得更大的利潤。上文的場景可以形式化地表示為時間最優的利潤最大化問題：給定每個時間單位的促銷成本cost，每件商品利潤price，用戶的歷史動作記錄L，要選擇時間長度T和種集S，使得S在時間T內的影響可以使商家獲取最大的利潤。顯然，選擇最佳的促銷時間長度有重要的應用價值。本文主要貢獻如下：

（1）利用用戶的歷史動作記錄，設計了基于時間長度的影響力分配模型IVA-T（influence value allocation-T），在該模型基礎上第一次提出了時間最優的利潤最大化問題（time optimal profitmaximization，OTPM），并證明了該問題是NP-hard問題。

（2）提出了一個近似算法Profit-Max來解決OTPM問題，同時證明了Profit-Max算法的近似比為1-1/e-β/e，其中β表示最優解的成本與最優解的純利潤的比值，是一個極小的數。

（3）通過在多個真實數據集上的實驗結果，得出以下結論：Profit-Max算法可以有效并高效地求解OTPM問題。另外，發現給定不同的時間長度，最終得到的種集是不一樣的。

本文組織結構如下：第2章介紹了相關工作；第3章給出了影響力分配模型及OTPM問題定義；第4章提出了基于動作日志的時間最優利潤最大化算法Profit-Max；第5章給出了實驗結果及分析；第6章對本文工作進行了總結。

2 相關工作

2003年，Kempe等人[2]第一次提出了社會網中的影響最大化問題，并利用貪心算法來解決該問題。每次迭代過程中選擇一個影響范圍增益最大的節點加入到種集，迭代循環到種集中節點數目為k。算法在選擇種子節點時，每次迭代都需要進行大量次數的蒙特卡羅模擬使得求解的影響范圍更為精確，然而效率會變低。2007年，Leskovec等人[7]提出了CELF（cost-effective lazy forward）優化算法改進貪心算法的效率，比原始貪心算法快700倍。Zhou等人[9]為影響范圍函數設計了一個上界，該上界可以減少在貪心算法中調用蒙特卡羅模擬的次數，尤其是在初始化的第一次迭代中，基于該上界，并結合CELF優化，設計了UBLF（upper bound based lazy forward）算法。Liu等人[10]也提出了一個線性的上界方法來計算影響力及影響最大化，設計了一個定量指標Group-Page-Rank，以便快速地在線性方法上估計影響力的上界，進一步提高影響最大化算法的效率。很多研究也將競爭因素結合到影響最大化研究中。Chen等人[11]擴展了IC傳播模型，提出了帶有時間限制的影響最大化問題。2012年，Lu等人[12]提出了LT-V模型，并在該模型上定義了利潤最大化問題。此后，Bhagat等人[13]提出LT-C傳播模型，并在該模型上研究并解決了最大化產品購買問題。Lin等人[14]考慮了現在社會網中很多相似商品之間的競爭關系，提出了基于學習的框架去解決多輪的競爭影響最大化，每個競爭者在選擇種集的時候不僅考慮了網絡信息，也考慮了對手的選擇，分別提出了已知對手策略和未知對手策略的解決辦法。

然而，上述模型都有如下弊端：邊上的概率值為預先設定，不能準確地模擬真實傳播。為解決該問題，Goyal等人[8]提出了基于動作日志來求解影響最大化問題。他們定義了基于數據傳播的CD模型，利用用戶的歷史行動日志來學習用戶之間的影響概率。在真實數據的傳播過程中有一個新的發現：給定不同的傳播時間，最終計算出的種集是不同的。而且，在現實營銷環境中，成本會隨著時間的推移而增加。因此，在利用動作日志精確選擇種集的基礎上，考慮不同的時間長度可以使最終選擇的種集具有更大的影響范圍。

3 傳播模型及問題定義

本章提出了一個考慮時間長度的影響力分配模型IVA-T，并給出了時間最優的利潤最大化問題（OTPM）的定義。

3.1 IVA-T傳播模型

給定有向圖G=(V,E)，時間長度T，動作日志L。動作日志L中記錄格式為(user,action,time)，表示用戶user在時間time執行了動作action。令V表示user的全集，A表示action的全集。對于任意u∈V,a∈A，令t(u,a)代表用戶u執行動作a的時間。現假設每一個用戶最多只執行某個動作一次。t(u,a)＜t(v,a)代表用戶u在用戶v之前執行過動作a；t(u,a)=+∞代表用戶u未執行過動作a。如果對于節點v，滿足0≤t(v,a)-t(u,a)≤T并且(u,v)∈E，則表示在時間T內，動作a從節點u傳播到節點v。

對于動作a，定義在T時間內，直接影響v的節點集合為Nin(v,a,T)={u|{u,v)∈E,0≤t(v,a)-t(u,a)≤T}。節點v在執行動作a時，v要對?u∈Nin(v,a,T)分配直接影響力，記作αv,u(a,T)，且滿足。對于直接影響力αv,u(a,T)，有多種分配方式。為便于理解，先定義αv,u(a,T)=1/Nin(v,a,T)。節點v迭代地為節點u的父節點w分配影響力，進一步判斷v與w的執行時間間隔是否滿足0≤t(v,a)-t(w,a)≤T，若滿足該條件，則需要給w分配影響力，否則不需要。給定動作a，節點v在時間T內給它的父節點w分配的影響力形式化地表示為，并 且Γu,u(a,T)=1。給定集合S?V，對于動作a，可以類似定義節點v在時間T內對S分配的影響力，如果u∈S，那么Γu,S(a,T)=1。最后，對動作日志中的每個動作聚集，得出最終影響力。節點v在時間T內給它的父節點w分配的影響力定義為，其中|Pv|表示節點v執行的動作個數。在時間T內，對于任意集合S?V，節點v對S分配的影響力表示為。以上描述的具有時間限制的傳播模型定義為IVA-T。在時間T內，給定IVA-T模型，種集S的影響范圍。

舉例來解釋提出的模型。給定一個有向圖G=(V,E)，其中V={1,2,3,4,5,6,7}，E={(1,2),(2,3),(2,4),(5,6),(5,7)}。動作日志L={(1,a,0),(5,a,0),(2,a,1),(6,a,1),(7,a,1),(3,a,3),(4,a,3)}。首先，對動作日志(u,a,t)做預處理：先按action排序，再按照time排序。利用IVA-T模型，先計算T=1時，圖G中節點的影響力分配，找到影響力最大的節點。當T=1時，對于動作日志記錄(1,a,0)，節點1先于其他節點執行動作a，因此節點1不給其他節點分配影響力；對于日志記錄(2,a,1)，掃描指向節點2的鄰接鏈表，因為0≤t(2,a)-t(1,a)≤1,(1,2)∈E，所以節點2給節點1分配的影響力為1/Nin(2,a,1)=1；同理，對于動作日志記錄(6,a,1)和(7,a,1)，得出節點6給節點5分配的影響力為1/Nin(6,a,1)=1，節點7給節點5分配的影響力也為1/Nin(7,a,1)=1；對于動作日志記錄(3,a,3)，掃描指向節點3的鄰接鏈表，因為t(3,a)-t(2,a)＞1，所以節點3不對節點2分配影響力。同理節點4也不對節點2分配影響力。當T=2時，采用上述方法進行影響力分配。當T=1，T=2時影響力分配的結果如表2所示。

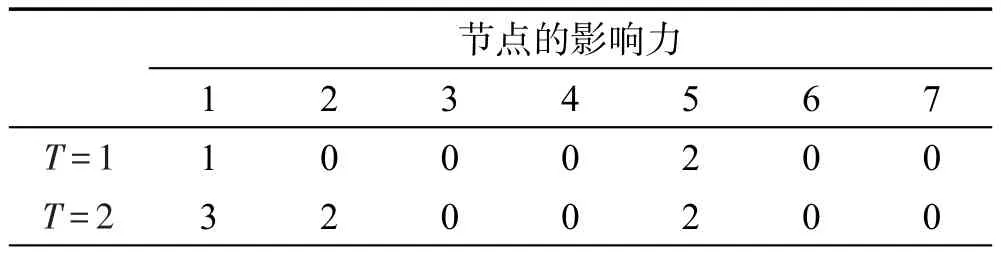
Table 2 Influence value of different timespan表2 在不同時間長度條件下分配的影響力

通過上述例子，發現在不同時間長度條件下，影響力最大的節點是不同的。例如，T=1時，節點5影響力最大；T=2時，節點1影響力最大。因此，在不同的時間長度條件下，應當選擇不同的種集。

3.2 問題定義

時間最優的利潤最大化問題（OTPM）：給定有向圖G=(V,E)，動作日志L(user,action,time)，每件商品的利潤price，單位時間的成本cost，正整數k，最佳促銷時間長度T，種集S，其中|S|=k，使得在IVA-T模型下，商品的純利潤price×δIVA-T(S,T)-cost×T達到最大，其中price×δIVA-T(S,T)表示在時間T內促銷商品獲得的利潤，cost×T表示在時間T內促銷的成本。

定理1最優的利潤最大化問題OTPM是NP-hard問題。

證明 如果把時間長度T設置為社會網中用戶執行動作的最大時間T=max{t(u,a)|u∈V}，那么IVA-T傳播模型等價于CD傳播模型[8]，使price=1，cost=0，則時間最優的利潤最大化問題OTPM可以轉化為影響最大化問題。Goyal已經證明影響最大化問題在CD傳播模型下是NP-hard問題。由于時間最優的利潤最大化問題的特殊情況是NP-hard，那么該問題也是NP-hard。 □

4 基于動作日志的利潤最大化算法

首先將時間均勻分為M個單位長度，對于每個遞增的時間長度，首先利用算法Initialization影響力分配鏈表inf_link進行初始化，再利用算法Greedy-CELF選擇種集S_temp，并計算當前時間長度所選擇的種集得到的利潤。如果當前利潤大于最大利潤，則依次替換當前最大利潤、種集S和最佳時間長度T。Profit-Max算法的偽代碼如算法1所示。

算法1 Profit-Max算法

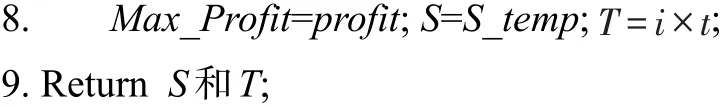
4.1 掃描動作日志，初始化影響力分配鏈表

算法Initialization按序掃描動作日志，針對動作a∈A，對每個節點u∈V的影響力分配鏈表inf_link[a][u]進行初始化。inf_link[a][u]中存儲節點u在動作a上為其他節點分配的影響力值。

首先，對動作日志L(user,action,time)進行預處理：先按動作action進行排序，然后按時間time排序。令active為存儲被目前動作激活的節點集合，P[u]代表節點u執行動作的個數，father[u]為節點u在目前動作上可激活的父節點集合，time[u]為節點u執行目前動作的時間。由給定有向圖G=(V,E)可構造指向每個節點u∈V的鄰接表in_edge[u]。順序掃描動作日志(u,a,t)，鄰接表in_edge[u]中的每個節點w，若w在active集合中，并且u執行目前動作的時間與w執行目前動作的時間間隔小于等于時間長度T，則把w加入節點u的影響力分配鏈表中，再對w進行影響力分配。然后迭代地對節點w的父節點進行影響力分配。算法2為Initialization算法的偽代碼。

算法2 Initialization算法

4.2 利用CELF優化選取節點

在選擇種集時使用了CELF算法。CELF算法利用函數的子模性。如果對?S?T，有φ(S∪{u})-φ(S)≥φ(T?{u})-φ(T)，則稱函數φ(?)具有子模性。易證，本文提出的影響傳播函數δIVA-T(S,T)在時間T固定時具有子模性，因此本文采用CELF算法進行種集選擇。

首先，Greedy-CELF算法利用Margin-compute計算節點u∈V的影響增益u.margin，更新當前迭代次數，再將u存儲到優先隊列queue。優先隊列queue將所有節點按margin的值從大到小排序。Greedy-CELF算法的偽代碼如算法3所示。

算法3 Greedy-CELF算法

4.3 對所有動作聚集，計算節點影響范圍增益

Margin-compute計算節點x加入種集S后影響范圍增益margin。gain[a]中存儲節點x每個動作上的影響力聚集值。SA[a][x]表示節點x針對動作a對當前種集S的影響力。那么針對動作a將x加入種集S，增益為gain[a]×(1-SA[a][x])。則基于所有動作，margin為增益gain[a]×(1-SA[a][x])的累加和。Margin-compute的偽代碼如算法4所示。

算法4 Margin-compute算法

4.4 更新影響力分配鏈表

將節點x加入到種集S后，算法Value-update更新了inf_link以及其他節點給當前種集S分配的影響力SA。算法Value-update的偽代碼如算法5所示。

算法5 Value-update算法

4.5 算法的時間復雜性分析

Profit-Max算法的時間復雜度為O(kηM|V||L|)。其中k為S的大小；η是所有節點的父節點數的最大值，即η=max{|inf_link[a][u]|,a∈A,u∈V}；|inf_link[a][u]|表示鏈表inf_link[a][u]的長度；M是時間段數；|V|是圖中節點數目；|L|為動作日志記錄數。

定理2 Profit-Max算法的近似比為1-1/e-β/e，其中β表示最優解的成本比上最優解的純利潤，即β=(cost×T0)/(price×δIVA-T(S0,T0)-cost×T0)。其中(S0,T0)是問題OTPM的最優解。

證明 本文提出在選擇最終種集S時，固定了時間長度T。當T為常數時，利用文獻[8]的定理2易證δIVA-T(S,T)具有子模性、單調性。因此當T為常數時，利用貪心算法可以找到一個與最優解的比值至少為1-1/e的近似解。為了便于閱讀，令α=1-1/e。設T=T0，S=S0是OTPM問題的最優解，Profit-Max算法在T=T0時找到的種集為S′，Profit-Max算法在求解OTPM問題時返回的解為T=T1，S=S1。那么有α×δIVA-T(S0,T0)≤δIVA-T(S′,T0)。因此price×δIVA-T(S0,T0)-cost×T0≤1/α×price×δIVA-T(S′,T0)-cost×T0=1/α×(price×δIVA-T(S′,T0)-cost×T0)+(1/α-1)× cost×T0≤ 1/α×(price×δIVA-T(S1,T1)-cost×T1)+(1/α-1)×cost×T0，從 而 1≤1/α×(price×δIVA-T(S1,T1)-cost×T1)/(price×δIVA-T(S0,T0)-cost×T0)+(1/α-1)×β。整理后，(price×δIVA-T(S1,T1)-cost×T1)/(price×δIVA-T(S0,T0)-cost×T0)≥(1-(1/α-1)×β)×α=α-(1-α)×β=1-1/e-β/e。 □

5 實驗與結果分析

在兩個真實數據集上測試和評估了本文提出的算法，并從多個角度驗證本文算法的有效性和高效性。

5.1 實驗環境描述

本文使用的兩個數據集都包含一個社會網G=(V,E)和一組動作日志L(user,action,time)。數據集分別是Last.fm[15]和Digg[15]。其中，Last.fm是社交音樂平臺，用戶可以評論音樂。動作日志中的信息代表用戶u在時間t評論音樂a。從中提取了2 100個節點，25 435條邊及相應的動作日志。該動作日志包含1 000個動作，21 646條記錄。Digg是社交新聞網站，用戶可以評論網站上的文章。動作日志中的信息代表用戶u在時間t評論文章a。從中提取了5 000個節點，395 513條邊及相應的動作日志。該動作日志包含500個動作，77 461條記錄。

實驗中所有算法均用C++編寫，在Microsoft Visual Studio 2010環境下編譯。所有實驗都在Intel?Core?2 Duo CPU，2 GB主存的臺式機上運行。

5.2 種集大小和時間長度對利潤的影響

本組實驗考察種集大小k和時間長度T對影響范圍Spread和利潤Profit的影響。從圖1和圖2可以看出，當時間長度T固定時，隨著種集大小k的增加，影響范圍Spread也在不斷增加。當k固定時，隨著時間長度T的增加，影響范圍Spread也在增加。

從圖3和圖4可以看出，固定k時，隨著時間長度T的增加，利潤不斷增加，但當時間達到某個點時，利潤不再增加。在Last數據集上T=6時，利潤Profit達到最大。而在Digg數據集上，利潤Profit在T=3時達到最大。由此可見選擇最佳促銷時間在營銷過程中的重要性。

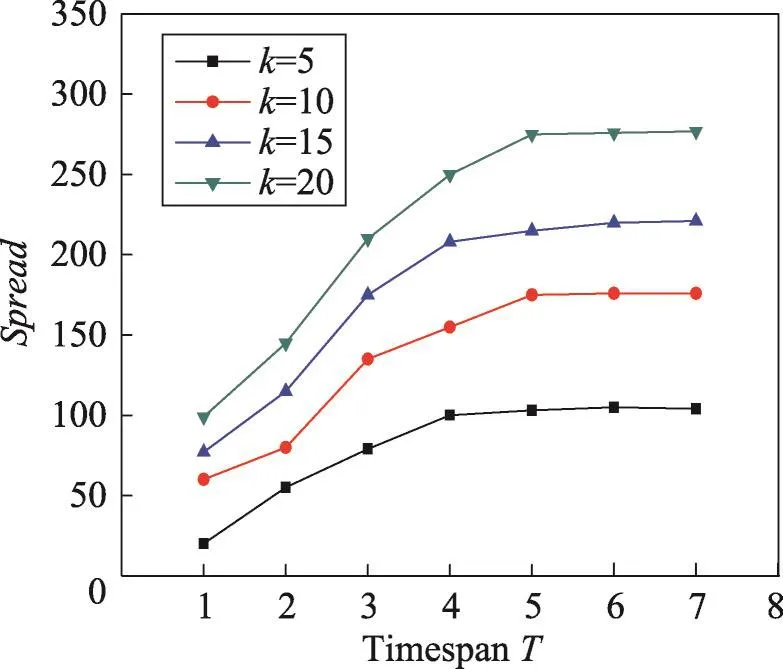
Fig.1 Spread vs timespan T in Last dataset圖1 在Last數據集上影響范圍vs時間長度T

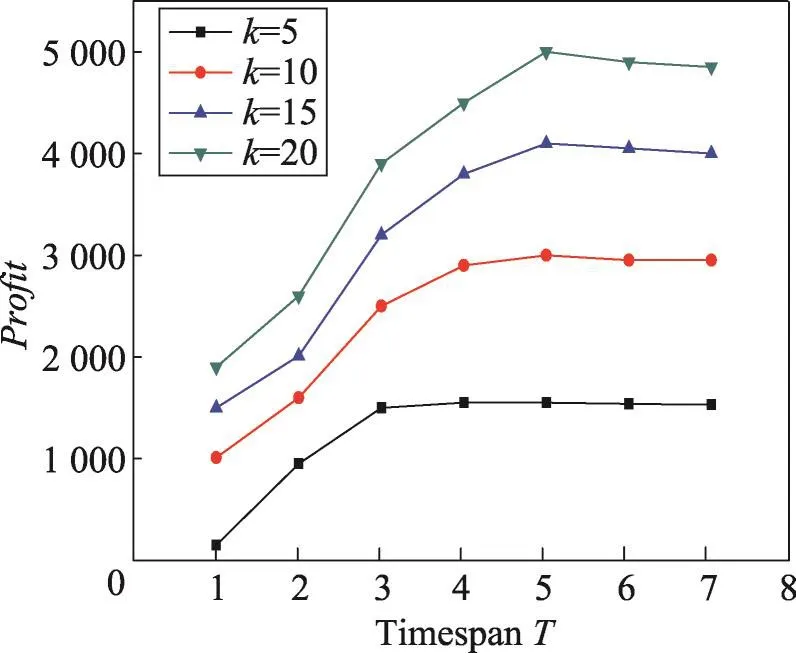
Fig.3 Profit vs timespan T in Last dataset(price=20,cost=100)圖3 在Last數據集上price=20,cost=100時產品利潤vs時間長度T

5.3 產品價格和成本對利潤的影響

本組實驗考察產品價格price和成本cost對利潤和最佳促銷時間的影響。由圖5可以看出，最佳促銷時間隨著price的增加也在不斷增加。當price=10時，T=3為最佳促銷時間。而當price=40時，T=6為最佳。由圖6可以看出，最佳促銷時間不斷減小。當cost=100時，T=6為最佳促銷時間。而當cost=400時，T=4為最佳。由此可見，在不同的產品價格price和成本cost條件下，選擇不同的促銷時間長度是重要的。

在Digg數據集上也做了相同的實驗，實驗結果得出的規律與在Last上的結果相似。

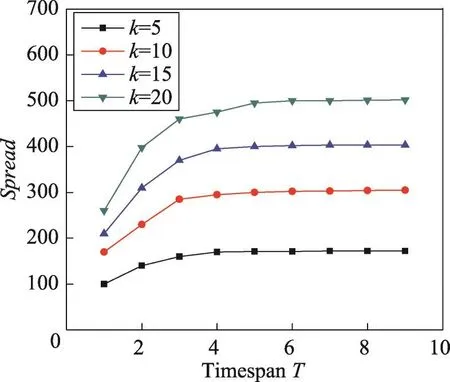
Fig.2 Spread vs timespan T in Digg dataset圖2 在Digg數據集上影響范圍vs時間長度T

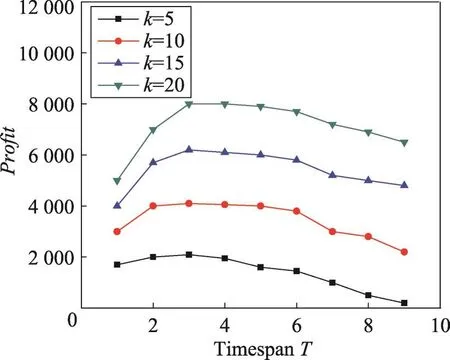
Fig.4 Profit vs timespan T in Digg dataset(price=20,cost=400)圖4 在Digg數據集上price=20,cost=400時產品利潤vs時間長度T

5.4 比較不同算法選擇的種集

本組實驗考察本文算法與其他算法在選擇的種集的真實影響范圍以及運行時間上的差異。主要與下面方法進行比較。（1）Degree-Max：選擇節點度數最大的k個節點作為種集；（2）Greedy-Max：使用貪心算法選取種集；（3）CD-Max：在CD模型上使用貪心算法選取種集；（4）LAIC-Max：在LAIC模型上根據時間長度選取種集；（5）IC-M-Max：在IC-M模型上根據時間長度選取種集。

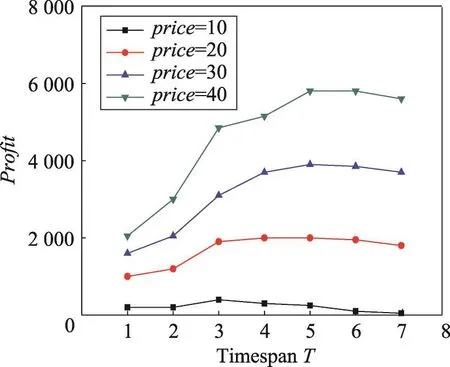
Fig.5 Profit vs timespan T in Last dataset(cost=300,k=10)圖5 在Last數據集上cost=300,k=10時產品利潤vs時間長度T

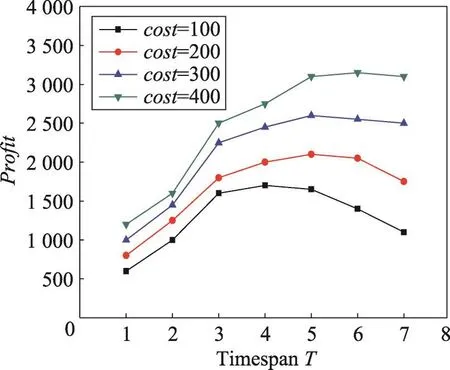
Fig.6 Profit vs timespan T in Last dataset(price=20,k=10)圖6 在Last數據集上price=20,k=10時產品利潤vs時間長度T

在這組實驗中，分別利用上述6種算法選擇k=10的種集，并計算選定種集在不同時間長度下影響范圍Spread。從圖7和圖8中可以看出，Degree-Max的結果最差，因為Degree-Max只是選擇全局具有最大度數的節點。Greedy-Max在計算影響范圍時采用了蒙特卡羅模擬估計，使得該算法結果略優于Degree-Max。LAIC-Max與IC-M-Max既考慮了圖的拓撲結構，也考慮了時間因素，但是在求解影響范圍時沒有利用真實數據，因此計算出的影響范圍不準確。CD-Max雖然利用了真實數據，但該算法在每個時間長度所選擇的種集S都是相同的。Profit-Max則在真實數據上計算影響范圍，根據不同的時間長度T，選擇最優種集S，因此得到的影響范圍優于其他算法。

從圖9中可以看出以上6種算法的運行時間。Degree-Max運行時間較快的原因是該算法只是簡單地選擇全局度數最大的k個節點作為種集。LAICMax與IC-M-Max的運行時間隨著時間長度的增加呈線性增加的趨勢。Profit-Max運行時間最快，是因為Profit-Max直接利用真實數據計算影響范圍。由于Greedy-Max方法需要大量次數蒙特卡羅模擬，使得運行時間太長，圖中沒有顯示。

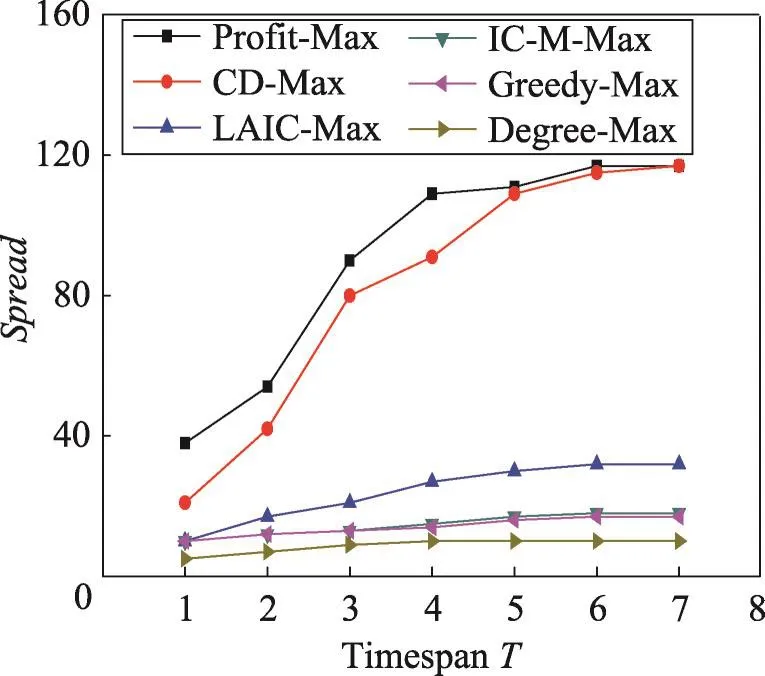
Fig.7 Spread vs timespan T in Last dataset(k=10)圖7 在Last數據集上k=10時影響范圍vs時間長度T

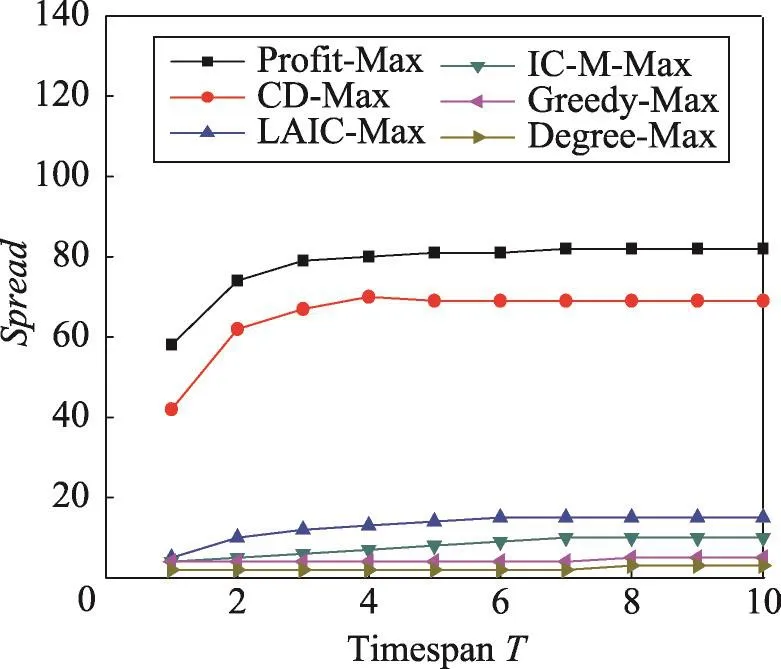
Fig.8 Spread vs timespan T in Digg1000 dataset(k=10)圖8 在Digg1000數據集上k=10時影響范圍vs時間長度T

選擇了7個不同的時間長度，分別計算出在這些不同時間長度下的種集。從表3中可以得出結論，在不同的促銷時間長度下，應選擇不同的種集。

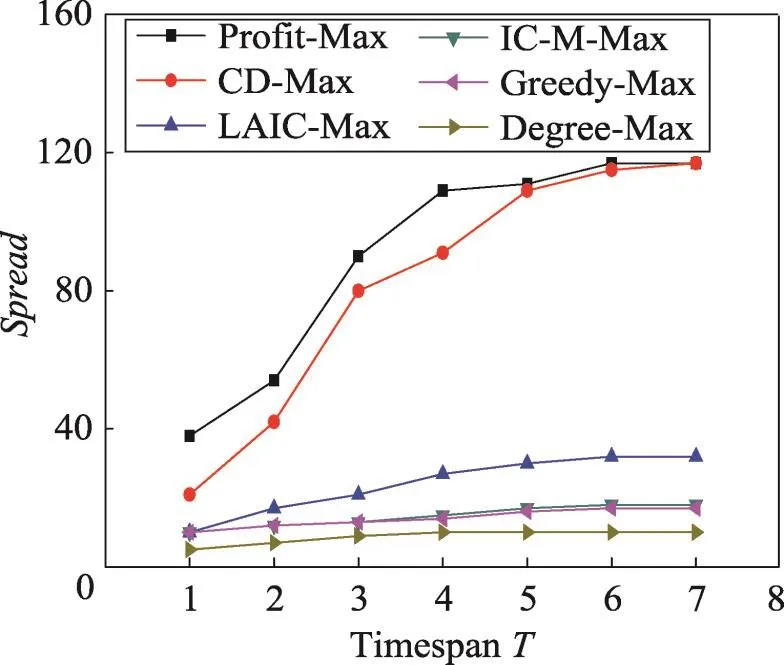
Fig.9 Running time vs timespan T in Digg1000 dataset(k=10)圖9 在Digg1000數據集上k=10時運行時間vs時間長度T

6 結束語

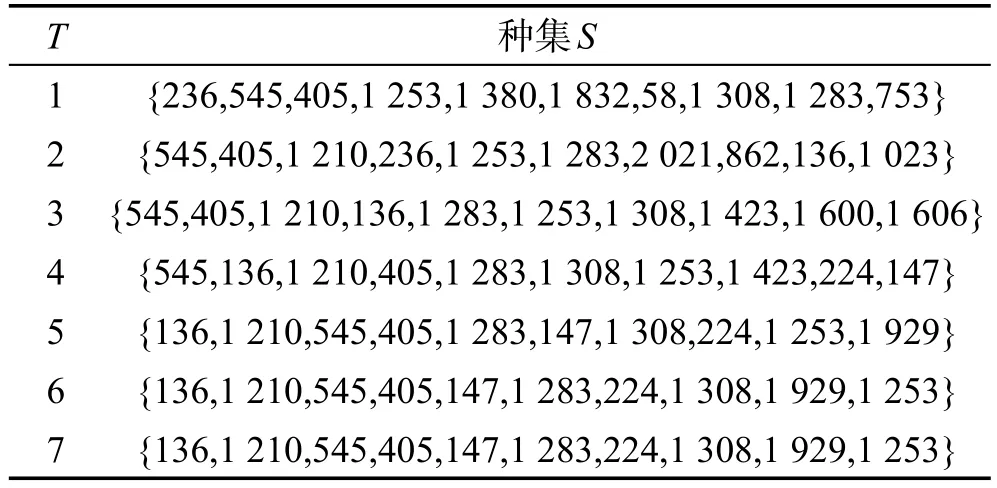
Table 3 Different time vs seed set length in Last dataset with k=10表3 在Last數據集上k=10時時間長度vs種集

本文提出了基于時間長度的影響力分配模型IVA-T，在其基礎上提出了時間最優的利潤最大化問題（OTPM），并證明了該問題是NP-hard問題。為解決該問題，提出了一個高效的近似算法Profit-Max，并證明了Profit-Max的近似比。多個數據集上的實驗結果證明了Profit-Max算法的有效性和高效率。

[1]Domingos P,Richardson M.Mining the network value of customers[C]//Proceedings of the 7th ACM SIGKDD Conference on Knowledge Discovery and Data Mining,San Francisco,USA,Aug 26-29,2001.NewYork:ACM,2001:57-66.

[2]Kempe D,Kleinberg J M,Tardos é.Maximizing the spread of influence through a social network[C]//Proceedings of the 9th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,Washington,Aug 24-27,2003.New York:ACM,2003:137-146.

[3]Chen Wei,Wang Yajun,Yang Siyu.Efficient influence maximization in social networks[C]//Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,Paris,Jun 28-Jul 1,2009.New York:ACM,2009:199-208.

[4]Chen Wei,Wang Chi,Wang Yajun.Scalable influence maximization for prevalent viral marketing in large-scale social networks[C]//Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,Washington,Jul 25-28,2010.New York:ACM,2010:1029-1038.

[5]Li Yuchen,Zhang Dongxiang,Tan K L.Real time targeted influence maximization for online advertisements[J].Proceedings of the VLDB Endowment,2015,8(10):1070-1081.

[6]Horel T,Singer Y.Scalable methods for adaptively seeding a social network[C]//Proceedings of the 24th International Conference on World Wide Web Companion,Florence,Italy,May 18-22,2015.New York:ACM,2015:623-624.

[7]Leskovec J,Krause A,Guestrin C,et al.Cost-effective outbreak detection in networks[C]//Proceedings of the 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,San Jose,USA,Aug 12-15,2007.New York:ACM,2007:420-429.

[8]Goyal A,Bonchi F,Lakshmanan L V S.A data-based approach to social influence maximization[J].Proceedings of the VLDB Endowment,2011,5(1):73-84.

[9]Zhou Chuan,Zhang Peng,Guo Jing,et al.An upper bound based greedy algorithm for mining top-kinfluential nodes in social networks[C]//Proceedings of the 23rd International World Wide Web Conference,Seoul,Apr 7-11,2014.New York:ACM,2014:421-422.

[10]Liu Qi,Xiang Biao,Chen Enhong,et al.Influence maximization over large-scale social networks:a bounded linear approach[C]//Proceedings of the 23rd International Conference on Information and Knowledge Management,Shanghai,Nov 3-7,2014.New York:ACM,2014:171-180.

[11]Chen Wei,Lu Wei,Zhang Ning.Time-critical influence maximization in social networks with time-delayed diffusion process[C]//Proceedings of the 26th Conference on Artificial Intelligence,Toronto,Canada,Jul 22-26,2012.Menlo Park,USA:AAAI,2012:592-598.

[12]Lu Wei,Lakshmanan L V S.Profit maximization over social networks[C]//Proceedings of the 12th International Conference on Data Mining,Brussels,Dec 10-13,2012.Washington:IEEE Computer Society,2012:479-488.

[13]Bhagat S,Goyal A,Lakshmanan L V S.Maximizing product adoption in social networks[C]//Proceedings of the 5th International Conference on Web Search and Data Mining,Seattle,USA,Feb 8-12,2012.NewYork:ACM,2012:603-612.

[14]Lin Suchen,Lin Shoude,Chen M S.A learning-based framework to handle multi-round multi-party influence maximization on social networks[C]//Proceedings of the 21st ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,Sydney,Australia,Aug 10-13,2015.New York:ACM,2015:695-704.

[15]Goyal A,Bonchi F,Lakshmanan L V S.Learning influence probabilities in social networks[C]//Proceedings of the 3rd International Conference on Web Search and Data Mining,New York,Feb 4-6,2010.New York:ACM,2010:241-250.

2016-08,Accepted 2017-02.

Research on Time Optimal Profit Maximization in Social Network*

LIU Yong+,XIE Shengnan,ZHANG Wei,ZHU Jinghua,WANG Nan
School of Computer Science and Technology,Heilongjiang University,Harbin 150080,China
+Corresponding author:E-mail:acliuyong@sina.com

Influence maximization is the problem of finding a small set of seed nodes in a social network.Existing works ignore the differences between influence spread maximization and profit maximization,and influence spread becomes stable when time passes by.This paper uses real action log and proposes a new propagation model with timespan which is called IVA-T(influence value allocation-T)propagation model,and firstly proposes time optimal profit maximization(OTPM)problem and proves that the problem is NP-hard.In order to solve the problem,this paper designs an effective approximation algorithm Profit-Max and analyzes the approximation ratio.The experimental results on several real datasets show that Profit-Max algorithm can solve OTPM problem effectively and efficiently.

social network;profit maximization;action log;timespan

10.3778/j.issn.1673-9418.1608044

*The Natural Science Foundation of Heilongjiang Province under Grant No.F201430(黑龍江省自然科學基金);the Innovation Talents Project of Science and Technology Bureau of Harbin under Grant No.2017RAQXJ094(哈爾濱科技創新人才研究專項資金項目);the Fundamental Research Funds of Universities in Heilongjiang Province,Special Fund of Heilongjiang University under Grant No.HDJCCX-201608(黑龍江省高校基本科研業務費黑龍江大學專項資金項目).

CNKI網絡優先出版:2017-03-01,http://kns.cnki.net/kcms/detail/11.5602.TP.20170301.1040.002.html

LIU Yong,XIE Shengnan,ZHANG Wei,et al.Research on time optimal profit maximization in social network.Journal of Frontiers of Computer Science and Technology,2017,11(11)：1723-1732.

A

TP311

LIU Yong was born in 1975.He received the Ph.D.degree in computer science from Harbin Institute of Technology in 2010.Now he is an associate professor and M.S.supervisor at School of Computer Science and Technology,Heilongjiang University.His research interests include data mining and database,etc.

劉勇（1975—），男，河北昌黎人，2010年于哈爾濱工業大學計算機科學專業獲得博士學位，現為黑龍江大學計算機科學技術學院副教授、碩士生導師，主要研究領域為數據挖掘，數據庫等。

XIE Shengnan was born in 1991.She received the M.S.degree from School of Computer Science and Technology,Heilongjiang University in 2015.Her research interest is data mining.

謝勝男（1991—），女，黑龍江黑河人，黑龍江大學計算機科學技術學院碩士研究生，主要研究領域為數據挖掘。

ZHANG Wei was born in 1989.She received the M.S.degree from School of Computer Science and Technology,Heilongjiang University in 2015.Her research interest is data mining.

張巍（1989—），女，黑龍江人，2015年于黑龍江大學計算機科學技術學院獲得碩士學位，主要研究領域為數據挖掘。

ZHU Jinghua was born in 1976.She received the Ph.D.degree in computer science from Harbin Institute of Technology in 2009.Now she is an associate professor and M.S.supervisor at Heilongjiang University.Her research interests include data mining and database,etc.

朱敬華（1976—），女，黑龍江齊齊哈爾人，2009年于哈爾濱工業大學計算機科學專業獲得博士學位，現為黑龍江大學計算機科學技術學院副教授、碩士生導師，主要研究領域為數據挖掘，數據庫等。

WANG Nan was born in 1980.She is a Ph.D.candidate at School of Electronic Engineering,Heilongjiang University.Her research interests include sensor network and social network,etc.

王楠（1980—），女，黑龍江哈爾濱人，黑龍江大學電子工程學院博士研究生，主要研究領域為傳感器網絡，社會網絡等。