初中數學教學中數學思想方法的應用

仇文華

數學思想與方法是數學知識的重要組成部分，一直貫穿在整個數學學習中，隨著數學的發展而逐漸完善，是數學解題思路的精髓所在.下面分析在初中數學教學中數學思想方法的應用.

一、在初中數學教學中數學思想方法的應用

1.數形結合思想.數與形是數學的兩個最古老、最基本的研究對象，它們在一定條件下可以相互轉換.數形結合思想，通過“以形助數”或者是“以數解形”，使復雜的問題簡單化，抽象的問題具體化、生動化.例如，求不等式組的解集：2（x+1）<3（x-1）+7，16x-3（3x-1）≤24.解題思路：由第一個不等式2（x+1）<3（x-1）+7可以得出x>-2，由第二個不等式可以得出x≤3.這時可以運用數形結合思想求解集.其中空心圓點表示不包含，實心圓點表示包含，大于向右畫區間，小于向左畫區間，兩個區間重疊的部分便是解集.

2.分類討論思想.分類討論思想是指，根據研究問題的特點和要求，分成不同類別，化整為零轉換成多個小問題來解決.這種按照不同類別分類，化繁為簡，再逐一解決的思想叫作分類討論思想.分類討論思想具有明顯的邏輯性、綜合性、探索性，在數學解題中占有重要的地位.

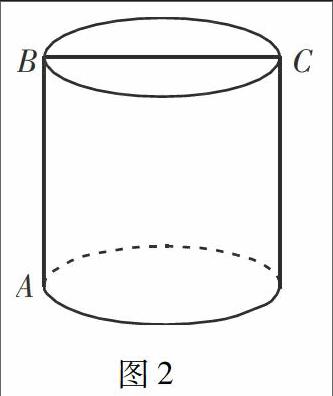
3.轉化思想.轉化思想是將復雜的問題轉化為常見的容易解決的問題，通過條件、結論等的轉換，化難為易、化繁為簡.在初中的數學解題中轉化思想無處不在.例如，一個圓柱體的底面周長為24cm，高AB為5cm，BC是直徑，一只螞蟻從A點出發沿圓柱體表面爬行到C點的最短距離是多少？解題思路：從A點爬到C點在曲面上會有無數條路線，然而選擇哪條最短呢，讓很多學生無從下手，若將這個圓柱體的側面展開，便成為學生所熟知的矩形，利用初中所學的知識兩點之間線段最短，便可將該問題轉換成直角三角形的問題，利用所給的已知條件獲知直角三角形的一邊長為5cm，再根據底邊圓形周長算出圓形半徑進而得知直角三角形另一條邊的長度，最后根據勾股定理可得最短距離.

二、在初中數學教學中應用數學思想方法的重要性

重視學生在解題中數學思想方法的應用，有助于學生的思維發展.從學生的心理發展進程來看，學生的思維模式處于形式思維到辯證思維的過渡時期，數學思想方法恰巧有利于這種思維的轉變.

加強數學思想方法的應用，有助于轉變教學模式.數學題往往存在舉一反三的現象，因此掌握一道題的答案并不是關鍵所在，而是需要掌握解題思路，這是精髓所在.學生掌握了相同題型的數學思想和方法，再做相同類型題時便會游刃有余.在教學中，教師不需要對每一道題進行詳細講解，只需將題目分門別類，挑選其中具有代表性的幾道題傳授其中的數學思想方法即可.

加強數學思想方法的應用，有助于轉變學習方式，數學是一門靈活的學科.學生在學習數學時應該掌握解題的數學思想方法.只要掌握了其中的數學思想方法，在面對相同題型時便會得心應手.數學中常常提到的“題海戰術”，并不是要求學生對同類型的題做的越多越好，否則既浪費了大量的時間，又得不到想要的效果，而是強調所見的題型多、所掌握的數學思想方法多.在學習數學時，學生要注重學習數學思想方法，提高學習效率.

加強數學思想方法的應用，有助于提高師生素質.在初中數學教學中，教師要滲透數學思想方法.一方面，有助于提高教師的素質.在教學中滲透數學思想方法，教師要作好課前準備，先對本節課所要教授的內容分門別類，然后在每一類別中選取具有代表性的例題.教師要隨時關注考題的變化和各種數學思想方法，完善自我的知識體系.另一方面，有助于提高學生的素質.在傳統的教學中，教師講的面面俱到，使學生即使沒有課前預習上課時也能跟上進度.而注重數學思想方法的教授，要求學生有自學能力，作好課前的預習準備，對即將學習的數學知識有大概的了解.這樣的方式，提高了學生的自學能力，有利于培養學生的思維能力.

總之，在初中數學學習中，每個版塊的知識并不是孤立存在的.看似碎片的數學知識都是相互聯系的.因此，在初中數學教學中，教師要滲透數學思想方法，發揮數學思想方法的作用.endprint