季節性差分時空地理加權回歸在HFRS分析中的應用

葛亮

(天津市測繪院，天津 300381)

季節性差分時空地理加權回歸在HFRS分析中的應用

葛亮*

(天津市測繪院，天津 300381)

為了更好地利用模型對湖北省腎綜合征出血熱(Hemorrhagic fever with renal syndrome，HFRS) 發病率數據的時間和空間分布進行擬合和預測，本文基于傳統的時空地理加權回歸模型(Geographically and Temporally Weighted Regression model，GTWR)，引入時間序列中的季節性差分方法，同時采用空間自相關法優化模型中的帶寬參數，構建了季節性差分時空地理加權回歸模型(Seasonal Difference-Geographically and Temporally Weighted Regression model，SD-GTWR)。研究結果表明，經過季節性差分優化的GTWR模型擬合精度要優于傳統的GTWR模型及最小二乘法模型(OLS)和地理加權模型(GWR)方法。

腎綜合征出血熱；時空地理加權回歸模型；季節性差分；空間分析；季節性差分時空地理加權回歸模型

1 引 言

隨著地理信息技術以及空間統計分析方法的不斷發展和完善，地理信息系統和空間統計學已經廣泛應用到各個領域。在空間計量學的基礎上，學者們提出眾多空間統計分析方法，其中，在1996年，英國學者Fotheringham提出了研究空間關系和空間相關關系的地理加權回歸模型(Geographical Weighted Regression，GWR)[1]，這一模型可以直觀地探測空間關系的非平穩性，目前該方法已經在人口、土地等多學科領域得以應用[2，3]。

隨著應用需求的不斷提高，很多行業領域空間數據的時間特性和空間特性(即時空特性)都顯得尤為突出。然而，GWR模型只將數據的空間特性納入到模型里，忽略了時間特性對其的影響[4～6]。因此，香港大學黃波教授于2010年在GWR模型的基礎上提出了時空地理加權回歸模型(Geographically and Temporally Weighted Regression，GTWR)[7]，并將其用于房價數據的分析。GTWR模型通過建立時空權重矩陣來計算空間信息的時空異質性。相較之GWR模型而言，時空地理加權回歸能夠更好對數據的時空分布及特性進行評估，有效地解決回歸模型的時空非平穩性。繼GTWR模型提出之后，眾多學者對模型本身的優化加以研究，如對其進行統計診斷和擬合等驗證[8，9]。同時，繼黃波教授利用該模型對房價數據進行分析后，又有學者在其他領域予以應用，如碳排放驅動因素等[10，11]。

腎綜合征出血熱(Hemorrhagic fever with renal syndrome，HFRS)是指由某些鼠類攜帶傳播的漢坦病毒引起的一類自然疫源性疾病[12]。近年來，國內外學者對腎綜合征出血熱的時空分布進行了大量的研究[13～15，19，20]，特別是通過對HFRS時空聚類分析的研究表明，HFRS具有極強的時空相關性[20]。就其發病規律的研究方面而言，學者們更多的是采用單一的時間或空間回歸分析方法對其發病規律進行擬合[16，17]。然而，單一的時間或者空間回歸分析的擬合研究效果相對單一。例如，在使用自回歸積分滑動平均模型(Autoregressive Integrated Moving Average Model，ARIMA)對HFRS數據進行擬合時，其對應的空間影響因子無法涉及；另外，在采用空間熱點和地理加權回歸時，HFRS數據所具有的時間特性便無法滿足[18，19]。因此，將時間因素和空間因素同時進行回歸計算，采用時空地理加權將能夠很好地對HFRS發病趨勢進行擬合與預測。

基于以上原因，本文嘗試融合季節差分的時空地理加權回歸模型探索湖北省HFRS發病率分布的時間和空間異質性。本文結合氣象相關影響因子以及人口、耕地等因素，建立GTWR回歸分析模型；在確定模型權重矩陣的帶寬時，采用空間自相關法確定帶寬的初始迭代值，模型計算次數約為原始方法計算次數的十分之一；同時融合湖北省HFRS分布的季節性特征，在傳統GTWR模型基礎上，構建SD-GTWR；并將差分GTWR方法與傳統的GTWR方法及最小二乘法模型(OLS)，地理加權模型(GWR)方法加以比較，得出針對湖北省HFRS發病率分析更優的擬合方法。

2 季節差分時空地理加權模型的構建

2.1時空地理加權模型原理

GTWR如式(1)所示：

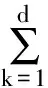
(1)

其中，ui表示觀測點i處的x坐標值，vi表示觀測點i處的y坐標值，ti表示觀測點i處的時間。(yi，xi1，xi2，…，xid)為在觀測點ui，vi，ti處對應的因變量Y和自變量X1，X2，…，Xd的觀測值(i=1，2，…，n)。d表示自變量的總數，n表示觀測點的數目。βkui，vi，ti(k=0，1，2，…，d)為在觀測點ui，vi，ti處的未知參數，是ui，vi，ti的任意函數。εi為常數項，并且滿足獨立同分布，一般假設均值為0，方差為σ2。對上式采用局部最小二乘法進行估計，并解矩陣微商方程組，得到在點ui，vi，ti處的參數估計為：

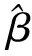
(2)

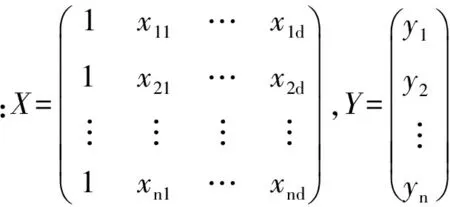
(3)

W(ui，vi，ti)=diag(w1(ui，vi，ti)，w2(ui，vi，ti)，…，wn(ui，vi，ti))

(4)

表示第i個觀測點數據的權重矩陣。

得出因變量Y在(ui，vi，ti)處的擬合值為：

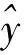
(5)

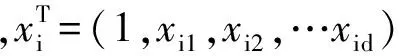
2.2空間權函數的定義及選取

為了完成上述回歸模型的估計，在計算任意回歸點ui，vi，ti處的權重矩陣時，需要計算研究區域內任意一點uj，vj，tj對該回歸點的一組權wij(j=1，2，…n)，其中wij的函數稱之為空間權函數。空間權函數的選擇和權重矩陣的計算方式會對計算結果產生直接的影響[21]。目前，在GTWR模型的估計中，常用的空間權函數有三立方(tri-cube)核函數法、高斯(Gauss)核函數法、雙平方根(bi-square)核函數法[8]。對于三立方核函數法，會出現回歸點觀測值權重無窮大的情況，因此在GTWR模型中不宜直接采用；對于高斯核函數方法，在計算每一點的空間權重時，研究區域內的所有點都將納入計算。然而，根據Tobler第一定理：空間上越相近，相關性就越強，隨著距離變大，相關性會減弱(Tobler，1979)。因此，隨著空間距離的變大，各行政區劃之間的HFRS發病率相關性會逐漸降低。可以看出，疾病發生的自相關性有一定的范圍限制，需要根據一定的空間范圍進行數據的篩選[22]。

因此，本文選用雙平方根核函數法將回歸點的參數估計影響較小的數據點去掉，從而剔除一些不必要的影響。雙平方根核函數法如式(6)和式(7)所示：

(6)

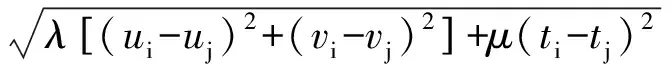
(7)

在式(6)中，dij表示回歸點ui，vi，ti到任一點uj，vj，tj的時空距離，h表示帶寬，代表權重wij與時空距離dij之間函數關系的一個非負衰減參數。在式(7)中，λ和μ作為時空比例因子，用于平衡時間距離和空間距離的影響，一般根據時間和空間范圍的跨度來進行設置。

2.3帶寬參數

在確定空間權函數后，參數估計的可靠性取決于帶寬函數。帶寬函數范圍選擇的主要方法有交叉驗證法、廣義交叉驗證法、Akaike信息準則(AIC)和貝葉斯信息準則(BIC)等方法。筆者在帶寬參數優化選擇的過程中發現，采用這些方法在進行計算時，需要進行反復的擬合，并且計算時間會隨著數據量的增加而顯著增加。同時，由于在計算的過程中，會出現多個跨度較大的帶寬值，其擬合優度檢驗參數(R2)相近。

空間自相關(Global Moran’s I)同時根據要素位置和要素值來度量空間自相關，而增量空間自相關則是使用一系列增大的距離運行空間自相關，同時測量各距離空間聚類的程度。在HFRS的時空數據分析中，只有當空間數據存在局部空間自相關時，該點的時空權重值才被認為是可靠的。因此，通過增量空間自相關的方式，可以擬合出一個比較適合的HFRS發病率空間自相關距離，并通過這個距離計算時空距離，再以此為基礎進行遞歸。

基于以上原理，本文首先使用增量空間自相關的方式，找出具有統計顯著性的Moran’s I檢驗峰值z的距離，并依此距離為基準，在一定范圍內進行交叉驗證，大大減少了交叉驗證過程中的數據計算量。

2.4季節性差分

在一個序列中，若經過S個(S為周期長度)時間間隔后呈現出相似性，我們認為該序列具有以S為周期的周期性特性。具有周期特性的序列就稱為季節性時間序列。本文通過對湖北省2007年～2010年的HFRS數據的時間趨勢分析，發現湖北省HFRS的發生具有較為穩定的季節性特征，如圖2所示。其時間分布特征表現為以年為單位呈現出雙峰型分布。因此，本文在對HFRS數據進行時空地理加權回歸前，先對其進行季節性差分，以提高時間序列數據的平穩性，從而得到更為可靠的評估結果。季節性差分表示為：

Wt=Xt-Xt-s

(8)

其中Wt為時間t處的差分結果。Xt表示當前月發病率值，Xt-s表示距離當前月S周期之前的發病率值。

3 HFRS的SD-GTWR模型

3.1湖北省HFRS數據

湖北省位于中國中部偏南，介于北緯29°05′～33°20′，東經108°21′～116°07′。本文選取了湖北省76個行政區從2007年～2010年的HFRS分月發病率數據，將其作為模型分析的因變量。模型選擇的自變量包括2007年～2010年各行政區的分月平均溫度、平均濕度、降雨量等氣象數據以及人口密度和耕地面積數據。其中湖北省行政區界數據來源于國家測繪地理信息局公開版1∶400萬地圖數據，HFRS數據來源于湖北省疾病預防控制中心，氣象數據來源于湖北省氣象局。

3.2算法流程

HFRS發病率數據時間和空間分析的擬合與預測流程如下：首先對數據進行季節性差分預處理，然后根據空間自相關分析的結果確定帶寬參數的初始值，通過權重矩陣和因變量擬合值的計算，判斷帶寬參數值是否符合檢驗標準。如不符合，則進行反復迭代，直至找出最優的帶寬參數，至此，模型建立完畢。如圖1所示。

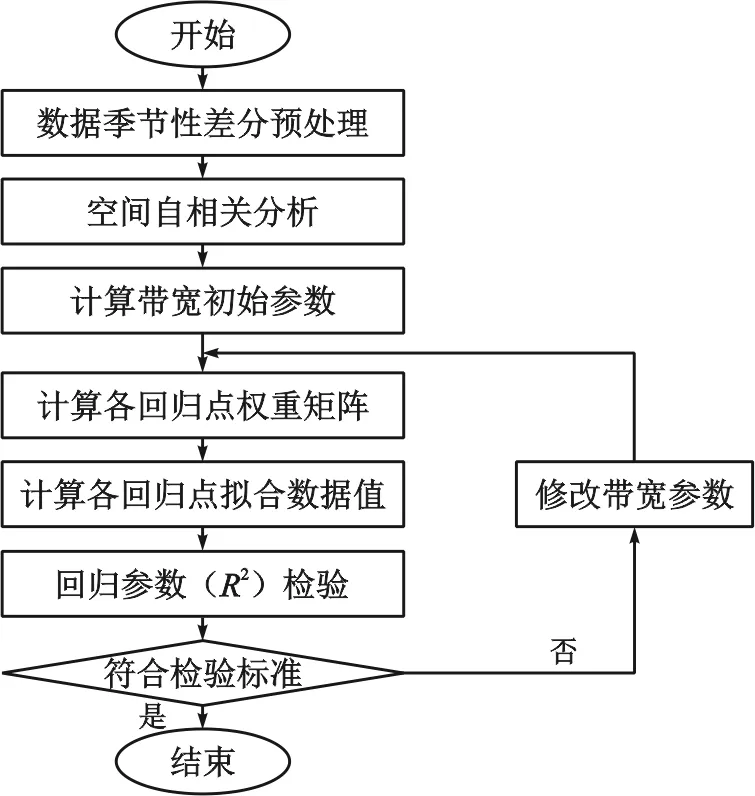
圖1 算法流程

3.3季節性差分分析

為了計算湖北省HFRS 2007年～2010年發病率季節性分布規律，對其分月發病率情況進行分析，計算結果如圖2所示。從圖中可以得出，湖北省HFRS 2007年～2010年發病率的季節性周期表現為5個月。

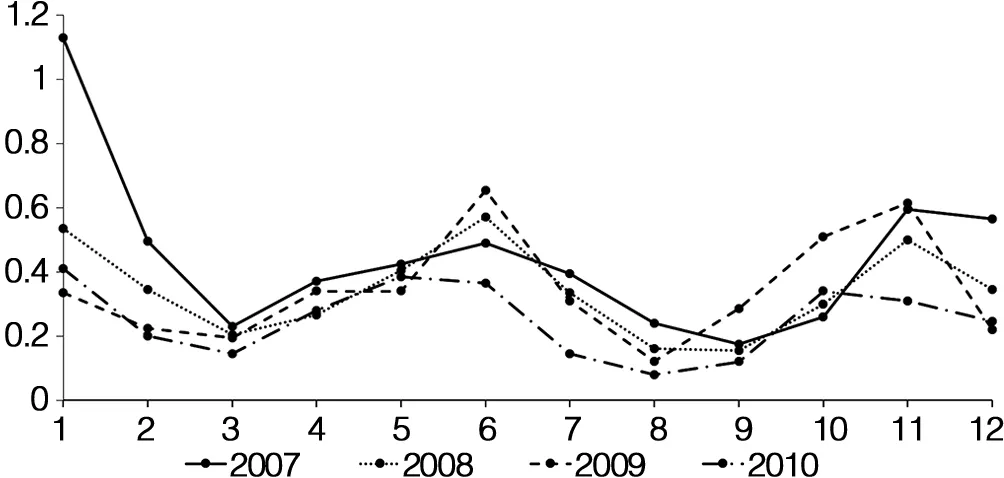
圖2 2007年～2010年湖北省月發病率

本文根據實驗數據建立自變量矩陣X(3648×6)，和因變量矩陣Y(3648×1)。并以5個月為周期，對HFRS發病率數據進行季節性差分，得到差分后的因變量矩陣YDif(3648×1)。

3.4帶寬參數的分析

本文選擇的空間權函數為雙平方根核函數，如式(6)和式(7)所示。計算湖北省HFRS發病率數據4年年平均發病率值，通過ArcGIS 10.2分別對HFRS發病率原始數據和差分后數據進行增量空間自相關運算，得到使z得分達到峰值的空間距離，計算結果如圖3所示。

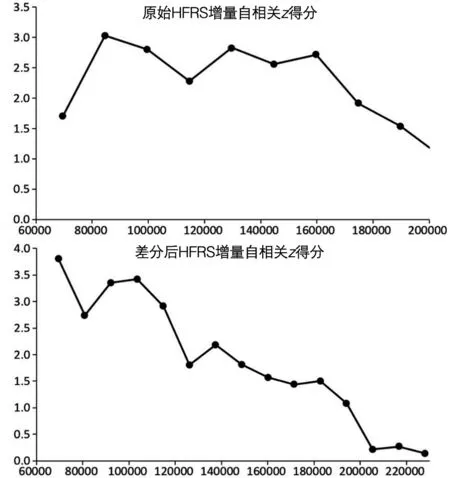
圖3 湖北省HFRS發病率增量自相關分析結果

從圖3中可以看出，其中原始發病率數據在距離為 84 605.26 m時，其z得分達到峰值為3.03，對應的Moran’s I指數為0.23。差分后的發病率數據在距離為 103 534.91 m時，其z得分達到峰值為3.41，對應的Moran’s I指數為0.17。因此，根據空間自相關分析的結果，本文選用的試驗數據中，時間數據跨度為48個月，距離跨度約 800 km，為了對時空數據進行平衡，設定空間因子λ為3，時間因子μ為50。結合帶寬值，使用MATLAB 2014b進行編程，計算出每一個時空回歸點的時空權重矩陣W(3 648×3 648)。在計算過程中發現，使用增量自相關進行距離模擬后，其模型擬合時間約為直接進行迭代時間的十分之一。

4 模型實驗結果比較與討論

本文針對HFRS發病率數據分別計算普通最小二乘法模型(OLS)，地理加權模型(GWR)，時空地理加權模型(GTWR)和季節性差分時空地理加權模型擬合優度檢驗參數(R2)以及標準化殘差，通過比較可以看出，無論從擬合優度還是標準化殘差來看，本文提出的季節性差分時空地理加權模型要優于OLS、GWR以及傳統的GTWR模型。如表1所示。

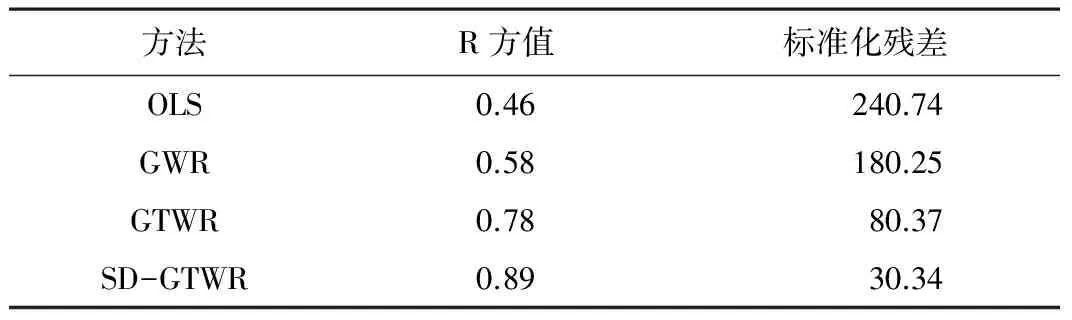
模型回歸分析結果 表1

從各模型的擬合度結果來看，SD-GTWR模型的擬合在湖北省HFRS的應用中具有穩定性和精準性，其原因如下：①空間因素對疾病的影響具有顯著性。湖北省不同縣市地理位置、周邊縣市發病率情況的不同。GWR和GTWR是將HFRS發病率數據的空間性質考慮在內，因此其模型擬合程度要高于普通最小二乘法；②時間特性和空間特性同時影響著疾病的發病率。GTWR在構建權重矩陣時同時對時間和空間數據加以計算，因此，其模型擬合精度要高于GWR；③季節性分布是HFRS近年來發病周期的顯著特征。對于具有明顯周期性變化的數據，要實現數據的平穩化，需要對其進行季節性差分處理，這樣方能消除時間周期性變化的影響。由于湖北省HFRS發病率數據表現出明顯的雙峰型季節性分布規律，基于這一研究發現，本文根據其時間變化規律，首先對發病率數據進行季節性差分，再將差分結果進行時空地理加權回歸擬合，這一結果較之GTWR的擬合度較高。同時，從方法使用的層面可以看出，單一時間回歸或空間回歸的優化方法，將其用在時間和空間同時考慮的時空地理加權回歸中同樣有效。

5 結 語

湖北省多年的HFRS發病數據同時與時間因素和空間因素有關。針對這一研究對象，本文引入GTWR模型，旨在解決湖北省HFRS時空異質性的問題。更進一步，針對湖北省HFRS發病率的季節性分布特征，本文在GTWR模型的基礎上，構建了SD-GTWR模型。SD-GTWR模型選用雙平方根核函數法，根據空間自相關的法則，對HFRS回歸點周邊的影響區縣進行過濾；通過選定合適的帶寬，對空間距離較大位置的數據進行篩選，能夠大幅度地減少模型的擬合次數。實驗表明，就回歸模型在湖北省HFRS發病率數據中的擬合而言，GTWR模型要明顯優于GWR模型和OLS模型，而本文提出的SD-GTWR模型要優于普通的GTWR模型。

[1] Fotheringham A B C C. Geographically Weighted Regression：the Analysis of Spatially Varying Relationship[M]. Repr. ed. Wiley：New York：2002：269.

[2] 邵一希，李滿春，陳振杰等. 地理加權回歸在區域土地利用格局模擬中的應用[J]. 地理科學，2010，30(1)：92～97.

[3] 張耀軍，任正委. 基于地理加權回歸的山區人口分布影響因素實證研究[J]. 人口研究，2012，36(4).

[4] 覃文忠，王建梅，劉妙龍. 混合地理加權回歸模型算法研究[J]. 武漢大學學報·信息科學版，2007，32(2)：115～119.

[5] 孟令奎，趙春宇，林志勇等. 基于地理事件時變序列的時空數據模型研究與實現[J]. 武漢大學學報·信息科學版，2003，28(2)：202～207.

[6] 李清泉，楊必勝，鄭年波. 時空一體化GIS-T數據模型與應用方法[J]. 武漢大學學報·信息科學版，2007，32(11)：1034～1041.

[7] Huang B. Geographically and temporally weighted regression for spatiotemporal modeling of house prices[J]. International Journal of Geographical Information Science，2010，24(3)：383～401.

[8] 劉美玲，王博，張雪敏. 時空地理加權回歸模型的統計診斷[J]. 西安文理學院學報·自然科學版，2013，16(2)：35～39.

[9] 玄海燕，李帥峰. 時空地理加權回歸模型及其擬合[J]. 甘肅科學學報，2011，23(4)：119～121.

[10] 易丹輝，肖宏偉. 基于時空地理加權回歸模型的中國碳排放驅動因素實證研究[J]. 統計與信息論壇，2014，29(2)：83～89.

[11] 王新剛，孔云峰. 基于時空窗口改進的時空加權回歸分析_以湖北省黃石市住房價格為例[J]. 地理科學，2015，35(5)：615～621.

[12] 劉曉冬. 中國腎綜合征出血熱時空分布及氣候因素對遼寧省HFRS影響的研究[D]. 山東大學，2012.

[13] 方立群. 腎綜合征出血熱時空分布及環境危險因素研究[D]. 北京：中國人民解放軍軍事醫學科學院 解放軍軍事醫學科學院，2009.

[14] W. Wu J Q G Z. GIS-based spatial，temporal，and space-time analysis of haemorrhagic fever with renal syndrome[Z]. Epidemiol. Infect，2009.

[15] Zhang Y H，Ge L，Liu L，et al. The epidemic characteristics and changing trend of hemorrhagic fever with renal syndrome in Hubei Province，China[J]. PLoS One. 2014，9(3)：e92700.

[16] Wang Y J，Zhao T Q，Wang P，et al. Applying linear regression statistical method to predict the epidemic of hemorrhagic fever with renal syndrome[J]. Chin J Vector Bio & Control，2006，17(4)：333～334.

[17] Feng X，Du S，Shu H. Spatial regression analysis in hemorrhagic fever with renal syndrome (HFRS) in China[C]//Spatial Data Mining and Geographical Knowledge Services (ICSDM)，2011 IEEE International Conference on. IEEE，2011：77～80.

[18] 郭秀花，曹務春，胡良平等. 腎綜合征出血熱發病率季節性時間序列預測模型[J]. 中國人獸共患病雜志，2003，19(4)：121，123.

[19] Li S，Ren H，Hu W，et al. Spatiotemporal Heterogeneity Analysis of Hemorrhagic Fever with Renal Syndrome in China Using Geographically Weighted Regression Models [J]. International Journal of Environmental Research and Public Health. 2014，11(12)：12129～12147.

[20] Wu W，Guo J，Guan P，et al. Clusters of spatial，temporal，and space-time distribution of hemorrhagic fever with renal syndrome in Liaoning Province，Northeastern China[J]. BMC Infectious Diseases. 2011，11(1)：229.

[21] 馮昕，杜世宏，舒紅. 空間權重矩陣對空間自相關的影響分析——以我國腎綜合征出血熱疾病為例[J]. 武漢大學學報·信息科學版，2011，36(12)：1410～1413.

[22] Lin H，Liu Q，Guo J，et al. Analysis of the geographic distribution of HFRS in Liaoning Province between 2000 and 2005[J]. BMC Public Health. 2007，7：207.

TheApplicationofHemorrhagicFeverwithRenalSyndrome(HFRS)AnalysisBasedonSeasonalDifference-GeographicallyandTemporallyWeightedRegression(SD-GTWR)

Ge Liang

(Tianjin Institute of Surveying and Mapping，Tianjin 300381，China)

In this paper，in order to obtain the fitting and prediction of the spatial and temporal characteristics of HFRS in Hubei province much better，a new model called SD-GTWR model was explained. Furthermore，this SD-GTWR model was associated with a combination of the traditional method model，seasonal difference method in time series and bandwidth parameters in the optimization model of spatial autocorrelation method. The results of the experiment proved that the accuracy of the SD-GTWR model is much higher than that of traditional GTWR model，OLS (Ordinary Least Square) and GWR (Geographical Weighted Regression).

hemorrhagic fever with renal syndrome；geographically and temporally weighted regression；seasonal difference；spatial analysis；seasonal difference-geographically and temporally weighted regression model

1672-8262(2017)05-34-05

P208

A

2017—09—08

葛亮(1989—)，男，博士，工程師，主要從事空間數據統計分析與地理信息系統應用研究。

國家自然科學基金項目(71503068)；中央高校業務經費重點發展領域科研專項項目(2015B09614)；

中央高校基本科研業務費項目(2014B15114)

本論文獲得2017年“華正杯”城市勘測優秀論文二等獎。