受污染混沌信號的協同濾波降噪?

陳越 劉雄英 吳中堂 范藝 任子良 馮久超

1)(華南理工大學電子與信息學院,廣州 510641)

2)(廣東技術師范學院電子與信息學院,廣州 510665)

受污染混沌信號的協同濾波降噪?

陳越1)劉雄英1)?吳中堂1)范藝2)任子良1)馮久超1)

1)(華南理工大學電子與信息學院,廣州 510641)

2)(廣東技術師范學院電子與信息學院,廣州 510665)

(2017年5月19日收到;2017年6月18日收到修改稿)

混沌信號,協同濾波,噪聲抑制

1 引 言

混沌行為常存在于生物、電氣、機械等物理系統[1],從觀測數據中檢測混沌是認識、分析和預測這些系統的關鍵.通常觀測信號是被噪聲污染的混沌行為,掩蓋了系統真實的動力學特性,有效抑制噪聲是分析和研究這些系統的前提.混沌信號固有的非周期、寬頻譜等特性使得傳統的線性和頻域濾波方法無法用于這類信號[2],因此,針對混沌信號的非線性動力學行為研究相應的降噪方法具有重要意義.

目前,受污染混沌信號的降噪問題正在引起學術界的關注,并提出了一些降噪方法[3?15]:梯度下降法對混沌信號降噪能獲得一條比原時間序列噪聲更小的時間序列軌道[3],但不能完全重構混沌信號;局部投影方法通過在參考點的鄰域近似吸引子的局部動力學行為來降噪[4,5],噪聲較強時由于鄰域半徑擴大導致性能下降嚴重;自然界中多數信號的小波變換是稀疏的,即只有少量變換系數顯著大于零[16],而高斯噪聲的能量則均勻分布在全部變換系數中,小波閾值法通過將較小的變換系數置零實現噪聲抑制,然后用逆變換重構混沌信號[6,7],這類方法的降噪效果在很大程度上取決于變換系數的稀疏程度,因此,必須選取合適的小波基;經驗模態分解(empirical mode decomposition,EMD)是一種數據驅動的分解方法,EMD閾值降噪[8]克服了小波閾值必須針對信號特征選取合適小波基的問題,并在混沌信號降噪中逐漸得到應用[9?11],但這類方法仍存在閾值、篩分迭代次數難以確定的問題;文獻[12]使用壓縮感知領域的基追蹤降噪技術來處理混沌信號,但為混沌信號構造“字典”是一個難題,從實驗結果看降噪效果也不理想;局部曲線擬合法[13]首先對數據進行分段,再利用多項式對分段數據做局部近似,最后通過加權平滑來重構混沌信號,文獻[14]通過自動搜索最佳擬合窗長進一步完善了這一方法,但由于混沌的高度非線性,局部線性近似難以實現精確的重構.已有算法本質上都是傳統非線性降噪方法在混沌信號上的應用,而不是針對混沌的某些特征專門設計的新方法,因此,它們在對混沌信號降噪時難以確保獲得好的效果.

自然圖像中包含大量的相似塊,如局部紋理、相似邊沿等,基于這一特性,Dabov等[17]提出了協同濾波的概念和著名的三維塊匹配(block matching 3D,BM3D)算法,該算法被認為是目前性能最好的彩色圖像降噪算法[18].在BM3D中,相似的二維(2D)圖像塊堆疊在一起形成3D分組,利用分組內圖像塊間的相似性對3D分組聯合濾波的過程被稱為協同濾波.

分形是混沌運動的基本特征之一,它在相空間體現為軌道的自相似結構[19],這意味著混沌信號在時域上也存在一定程度的自相似性.文獻[20]在Mackey-Glass,Lorenz等信號的時域波形中觀察到明顯的自相似特征,并將之歸因為混沌吸引子的自相似結構和自仿射分形特性;文獻[21]發現中心頻率附近出現的連續頻段導致了Duffing信號波形的自相似,并認為混沌信號具有頻率調制的相似性.本文利用混沌信號的這種自相似特性,將協同濾波的方法用于受污染混沌信號的降噪.在設計降噪算法的過程中,首先在觀測信號中搜索相似的片段并建立分組,然后在二維變換域用閾值法對每個分組做協同濾波,再經反變換得到分組中各片段的濾波結果,最后根據所有分組的濾波結果重構原信號.由于同一分組內的片段具有良好的相關性,與直接對觀測信號做一維變換相比,分組的二維變換能更稀疏的表示原信號.

2 混沌信號協同濾波降噪算法

混沌的分形特性表現為混沌信號在相空間具有自相似結構,這意味著其時域波形也存在一定的自相似性.圖1是一段被噪聲污染的Lorenz混沌信號,可以看到,信號波形具有自相似性,圖中用不同線型框標示了波形中的部分相似片段.

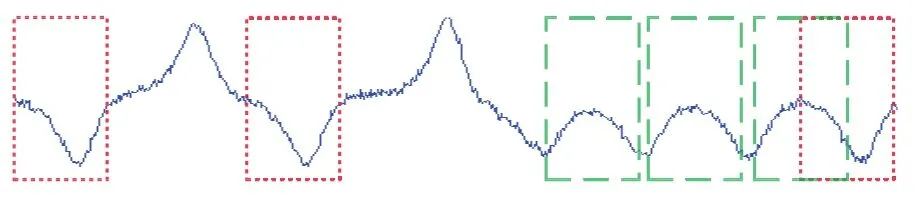
圖1 (網刊彩色)Lorenz信號的自相似性Fig.1.(color online)Self-similarity property of Lorenz signal.

利用混沌信號的這種自相似性抑制噪聲的流程如圖2所示,它包括分組、協同濾波和重構三個步驟:首先,從觀測信號中建立若干相似分組;然后,對每個分組進行協同濾波;最后,利用各分組的濾波結果重構原信號.

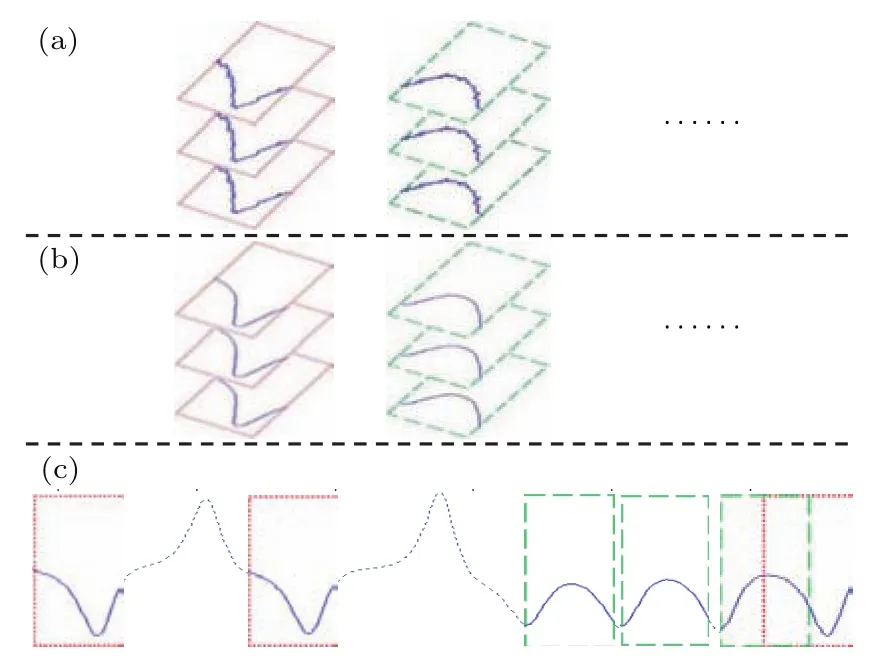
圖2 (網刊彩色)降噪算法流程示意圖 (a)分組;(b)協同濾波;(c)重構Fig.2.(color online)Process of the proposed denoising algorithm:(a)Grouping;(b)collaborative filtering;(c)reconstruction.

2.1 分 組

記參考片段為R,任意片段S與R的相似程度可以用二者的歸一化距離來度量[17]:

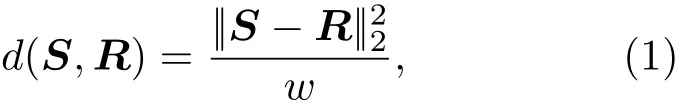
其中,w是片段寬度,該距離越小,S與R的相似程度越高.

以參考片段R為中心在長度為l(l?w)的窗口內搜索,找到與R距離最小的m個片段形成分組group(R),并保存到m行w列的二維數組中,即group(R)∈Rm×w.讓參考片段以步長δ從觀測信號的起始位置開始向后移動,搜索窗口也隨之移動.記錄在每個位置得到的相似分組,并標記分組中每個片段的位置.

2.2 協同濾波

協同濾波以分組為單位進行,分組內任一片段的濾波將用到同組其他片段的信息,因此可以看作是一個相互“協作”的過程[17].協同濾波包括以下步驟.

1)對分組做二維變換:

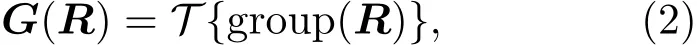
其中,G=[gi,j]∈Rm×w(i=1,···,m;j=1,···,w) 是變換系數矩陣,T[·]是二維離散余弦變換(DCT)或二維小波等任意等距線性變換.本文后續將采用DCT變換.

2)為每個分組選定一個閾值λ(R)并在變換域做閾值降噪,將小于閾值的系數置零來衰減噪聲,保留大于閾值的系數.閾值函數HT(·)由下式定義:

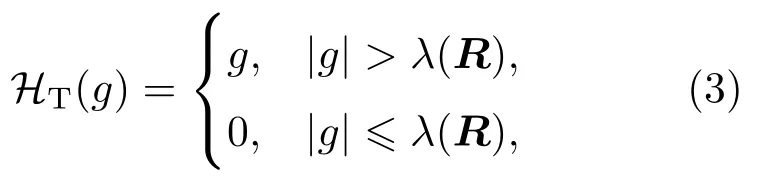
閾值λ(R)使用Donoho和Johnstone提出的Visu-Shrink方法[16]確定,該方法在均方誤差意義上是近似最優的,同時重構信號能保持原信號的光滑性[22],特別適合于處理混沌流信號.VisuShrink閾值定義為

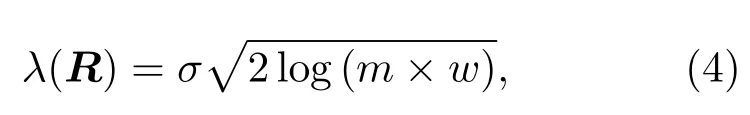
其中,σ是觀測信號的噪聲標準差,當噪聲強度未知時它可以由系數矩陣G(R)的中位數絕對偏差來估計[16]:

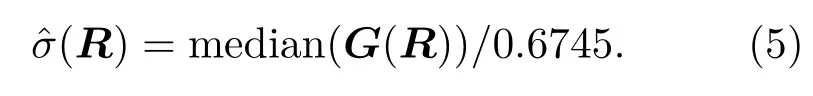
3)對變換系數G(R)做閾值后,通過逆變換得到分組的濾波結果:

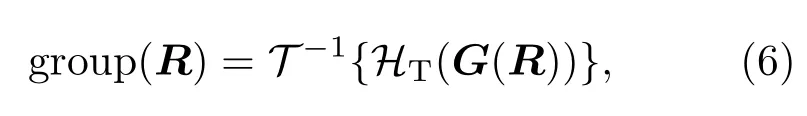
它包含了參考片段R對應分組的每個片段的降噪估計.

2.3 信號的重構

由2.1節的描述可知,片段間存在重疊.一般來說一個信號點會同時屬于多個不同片段,這些片段在該點的濾波結果也會不同.最終的降噪結果可以逐點計算,每個重構信號點由所有包含該點的片段在此處的濾波輸出做算術平均得到:

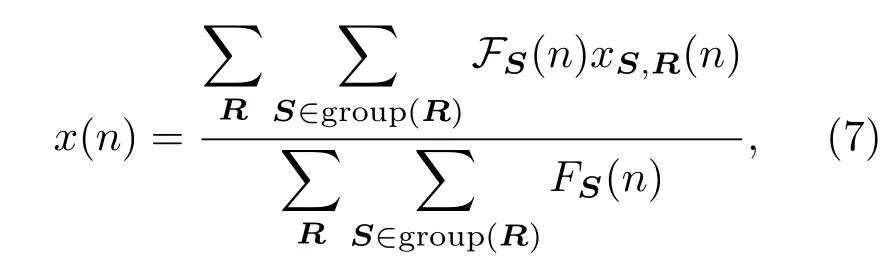
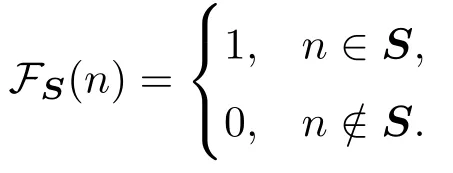
3 算法參數分析

本節以疊加高斯白噪聲的Lorenz信號為例討論算法參數對性能的影響.Lorenz系統的方程為

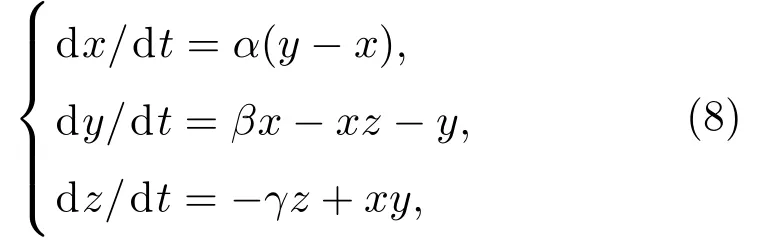
其中,參數α=10,β=28,γ=8/3.方程通過四階龍格-庫塔法求解,步長為0.01.在每次實驗中,方程從混沌區的隨機位置開始迭代,然后由狀態變量x產生混沌信號.算法性能通過輸出信噪比(SNRout)衡量,在相同的輸入信噪比(SNRin)下,SNRout越高表明降噪效果越好.SNR定義為

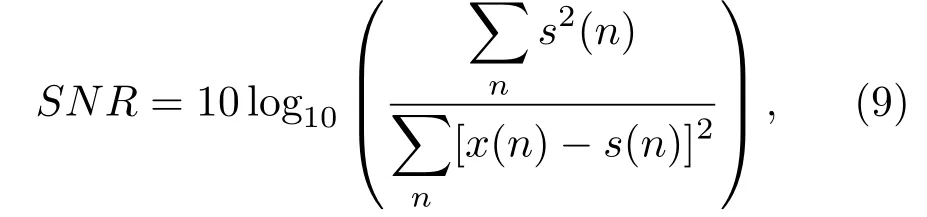
其中,s(n)為純凈的混沌信號,在計算SNRin時x(n)是含噪觀測信號,在計算SNRout時x(n)是降噪算法的輸出.

協同濾波降噪算法需要指定的參數有:片段寬度w、搜索窗長l、搜索窗移動步長δ和分組片段數m.分組片段數m對性能的影響非常有限,在后面的討論中將它固定為m=30.

3.1 片段寬度w

取搜索窗長l=4000,搜索窗移動步長δ=30,圖3顯示了片段寬度w與降噪效果的關系.一般,樣點數量不足會導致降噪算法的性能下降,當w較小時SNRout偏低,因此,w的取值不應小于100.

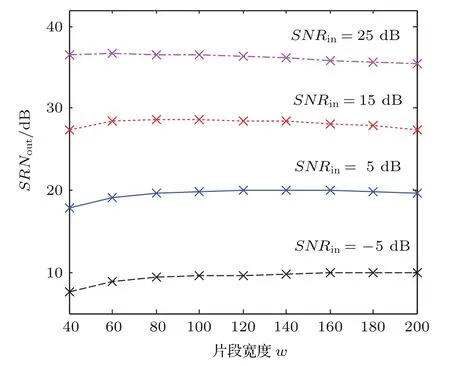
圖3 不同SNRin下SNRout與w的關系Fig.3.SNRoutversus w at different SNRin.

3.2 搜索窗長l

窗長l越長,分組越能在較大范圍內搜集相似片段,算法性能也就越好,圖4(w=120,δ=30)反映了l與降噪性能的這一關系.考慮到l增大會增加算法的復雜度,并且l較大后性能提升并不明顯,折中后選取l為4000左右.如果要獲得最佳性能,可以將整個觀測信號作為搜索范圍.

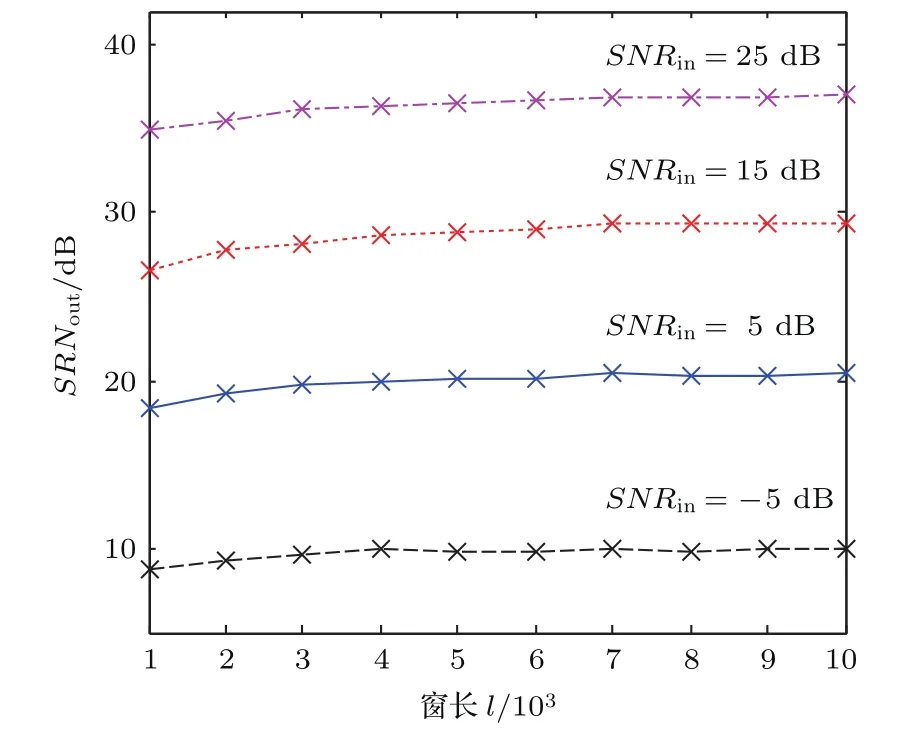
圖4 不同SNRin下SNRout與l的關系Fig.4.SNRoutversus l at different SNRin.

3.3 搜索窗移動步長δ

圖5 (w=120,l=4000)顯示了搜索窗移動步長δ與SNRout的關系.步長δ越小建立的相似分組就越多,對觀測信號的分析也越精細,因此,SNRout隨步長δ減小逐漸提高.由于δ減小會顯著增加算法的復雜度,一般折中選取δ為片段寬度w的1/2到1/4左右.

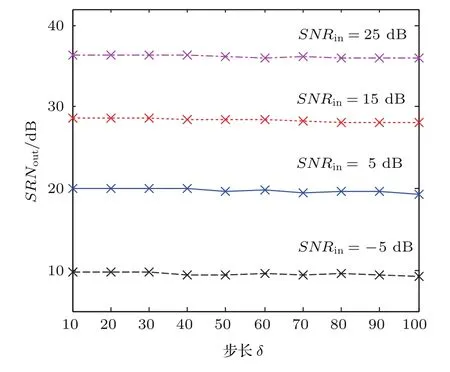
圖5 不同SNRin下SNRout與δ的關系Fig.5.SNRoutversus δ at different SNRin.

4 實驗結果

本節通過仿真實驗評估協同濾波降噪算法的性能,算法參數為w=120,l=4000,δ=w/4,觀測信號由Lorenz信號疊加高斯白噪聲生成.為了顯示算法的優越性,還與以下算法進行了比較:參考文獻[14]的方法,自動搜索最佳擬合窗長的局部曲線擬合算法[13];小波閾值降噪算法[6],用db8小波作基函數,分解4層,采用軟閾值;EMD迭代區間閾值(EMD iterative interval thresholding,EMD-IIT)法[8],篩分9次,迭代15次.算法性能通過SNRout、重構的均方誤差(root mean square error,RMSE)和對相圖的還原情況進行比較.RMSE定義為

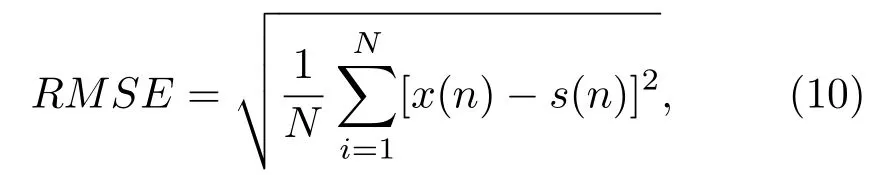
其中,s(n)是純凈的混沌信號,x(n)是降噪算法的輸出.

取信號長度為10000,圖6顯示了不同噪聲強度下各種算法降噪后的SNRout,圖7顯示了重構信號與純凈混沌信號的均方誤差,結果由100次隨機實驗平均得到.可以看到,局部曲線擬合法的性能略好于小波閾值,EMD-IIT法在低信噪比下性能較差.本文算法在實驗中表現出較好的噪聲抑制能力,其SNRout比另外三種方法高2.5—4 dB,從RMSE來看本文算法的重構精度也明顯優于其他方法.

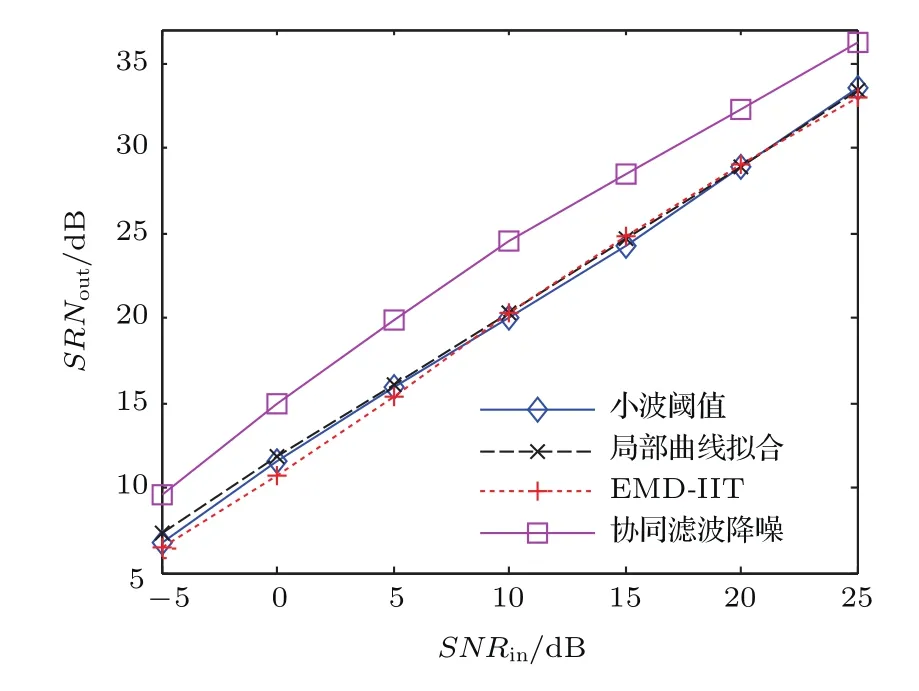
圖6 (網刊彩色)不同算法的SNRout比較Fig.6.(color online)SNRoutcomparison among different algorithms.

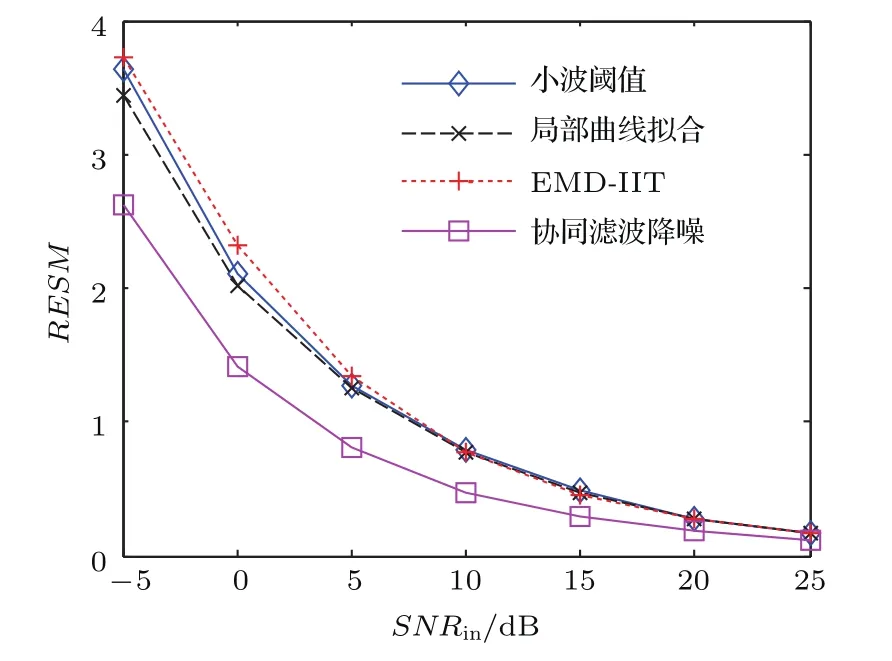
圖7 (網刊彩色)不同算法的均方誤差比較Fig.7.(color online)RMSE comparison among different algorithms.

對SNRin=10 dB的Lorenz信號進行降噪實驗,幾種算法重構的相圖如圖8所示.可以看到,觀測信號的相空間被噪聲湮沒,幾乎觀察不到分形特征.如圖8(c)—(e)所示,局部曲線擬合、小波閾值和EMD-IIT算法都能大致還原純凈吸引子的相圖,但由于軌道扭曲變形,使得原本有序的自相似結構顯得雜亂無章.從圖8(f)可見,本文算法重構的相圖具有更光滑的軌道,吸引子在相空間完整的分形結構也被更好地保留了下來.

5 結 論

結合混沌信號的自相似分形特性,本文提出了一種基于協同濾波的降噪算法.該算法的創新之處在于通過對相似片段分組將一維信號的降噪轉化為一個二維聯合濾波問題.由于相似片段間具有良好的相關性,與直接在一維變換域做閾值降噪相比,對分組的二維變換能獲得原信號更稀疏的表示,從而更好地抑制噪聲.仿真結果表明:本文算法在信噪比提升和重構精度上明顯優于小波閾值、局部曲線擬合等現有的混沌信號降噪算法;從對相圖的還原情況來看,本文算法重構的吸引子具有更清晰的自相似結構和更光滑的軌道,對純凈混沌吸引子的還原也更加準確.所以,協同濾波結合混沌自相似特性對受污染混沌信號進行降噪,在重構原始混沌信號方面具有較大的應用潛力.

圖8 Lorenz吸引子相圖 (a)無噪聲污染;(b)噪聲污染;(c)局部曲線擬合降噪;(d)小波閾值降噪;(e)EMD-IIT降噪;(f)本文算法降噪Fig.8.Phase portraits of Lorenz attractor reconstructed from(a)clean signal,(b)noisy signal,(c)signal denoised by local curve fitting,(d)signal denoised by wavelet thresholding,(e)signal denoised by EMD-IIT,(f)signal denoised by the proposed method.

[1]Feng J C 2012Chaotic Signals and Information Processing(Beijing:Tsinghua University Press)pp32–35(in Chinese)[馮久超 2012混沌信號與信息處理 (北京:清華大學出版社)第32—35頁]

[2]Badii R,Broggi G,Derighetti B,Ravani M,Ciliberto S,Politi A,Rubio M A 1988Phys.Rev.Lett.60 979

[3]Liu X Y,Qiu S S,Lau C M 2005J.Syst.Eng.Electron.16 253

[4]Cawley R,Hsu G H 1992Phys.Rev.A46 3057

[5]Leontitsis A,Bountis T,Pange J 2004Chaos14 106

[6]Han M,Liu Y H,Xi J H,Guo W 2007IEEE Signal Proc.Lett.14 62

[7]Constantine W L B,Reinhall P G 2001Int.J.Bifurcat.Chaos11 483

[8]Kopsinis Y,McLaughlin S 2009IEEE Trans.Signal Proc.57 1351

[9]Wang X F,Qu J L,Gao F,Zhou Y P,Zhang Y X 2014Acta Phys.Sin.63 170203(in Chinese)[王小飛,曲建嶺,高峰,周玉平,張翔宇2014物理學報63 170203]

[10]Wei X L,Lin R L,Liu S Y,Zhang C H 2016Shock Vib.2016 1

[11]Wang W B,Zhang X D,Wang X L 2013Acta Phys.Sin.62 050201(in Chinese)[王文波,張曉東,汪祥莉 2013物理學報62 050201]

[12]Li G M,Lü S X 2015Acta Phys.Sin.64 160502(in Chinese)[李廣明,呂善翔 2015物理學報 64 160502]

[13]Tung W W,Gao J B,Hu J,Yang L 2011Phys.Rev.E83 046210

[14]Wang M J,Wu Z T,Feng J C 2015Acta Phys.Sin.64 040503(in Chinese)[王夢蛟,吳中堂,馮久超2015物理學報64 040503]

[15]Hu J F,Zhang Y X,Yang M,Li H Y,Xia W,Li J 2016Nonlinear Dynam.84 1469

[16]Donoho D L,Johnstone I M 1994Biometrika81 425

[17]Dabov K,Foi A,Katkovnik V,Egiazarian K 2007IEEE Trans.Image Proc.16 2080

[18]Lebrun M 2012Image Proc.On Line2 175

[19]Yu S M 2011Chaotic Systems and Chaotic Circuits(Xi’an:Xidian University Press)pp10–12(in Chinese)[禹思敏2011混沌系統與混沌電路(西安:西安電子科技大學出版社)第10—12頁]

[20]He T,Zhou Z O 2007Acta Phys.Sin.56 693(in Chinese)[賀濤,周正歐 2007物理學報 56 693]

[21]Tang Y F,Liu S L,Lei N,Jiang R H,Liu Y H 2012Acta Phys.Sin.61 170504(in Chinese)[唐友福,劉樹林,雷娜,姜銳紅,劉穎慧2012物理學報61 170504]

[22]Coifman R R,Donoho D L 1995Lect.Notes Stat.103 125

PACS:05.45.—a,05.40.Ca DOI:10.7498/aps.66.210501

*Project supported by the National Natural Science Foundation of China(Grant No.61372008)and the Science and Technology Planning Project of Guangdong Province,China(Grant Nos.2015B010101006,2014A010103014).

?Corresponding author.E-mail:liuxy@scut.edu.cn

Denoising of contaminated chaotic signals based on collaborative filtering?

Chen Yue1)Liu Xiong-Ying1)?Wu Zhong-Tang1)Fan Yi2)Ren Zi-Liang1)Feng Jiu-Chao1)

1)(School of Electronic and Information Engineering,South China University of Technology,Guangzhou 510641,China)
2)(School of Electronic and Information Engineering,Guangdong Polytechnic Normal University,Guangzhou 510665,China)

d 19 May 2017;revised manuscript

18 June 2017)

Reconstructing chaotic signals from noised data plays a critical role in many areas of science and engineering.However,the inherent features,such as aperiodic property,wide band spectrum,and extreme sensitivity to initial values,present a big challenge of reducing the noises in the contaminated chaotic signals.To address the above issues,a novel noise reduction algorithm based on the collaborative filtering is investigated in this paper.By exploiting the fractal self-similarity nature of chaotic attractors,the contaminated chaotic signals are reconstructed subsequently in three steps,i.e.,grouping,collaborative filtering,and signal reconstruction.Firstly,the fragments of the noised signal are collected and sorted into different groups by mutual similarity.Secondly,each group is tackled with a hard threshold in the two-dimensional(2D)transforming domain to attenuate the noise.Lastly,an inverse transformation is adopted to estimate the noise-free fragments.As the fragments with in a group are closely correlated due to their mutual similarity,the 2D transform of the group should be sparser than the one-dimensional transform of the original signal in the first step,leading to much more effective noise attenuation.The fragments collected in the grouping step may overlap each other,meaning that a signal point could be included in more than one fragment and have different collaborative filtering results.Therefore,the noise-free signal is reconstructed by averaging these collaborative filtering results point by point.The parameters of the proposed algorithm are discussed and a set of recommended parameters is given.In the simulation,the chaotic signal is generated by the Lorenz system and contaminated by addictive white Gaussian noise.The signalto-noise ratio and the root mean square error are introduced to measure the noise reduction performance.As shown in the simulation results,the proposed algorithm has advantages over the existing chaotic signal denoising methods,such as local curve fitting,wavelet thresholding,and empirical mode decomposition iterative interval thresholding methods,in the reconstruction accuracy,improvement of the signal-to-noise ratio,and recovering quality of the phase portraits.

chaotic signal,collaborative filtering,noise reduction

根據混沌吸引子的自相似分形特性,提出了一種利用協同濾波重構受污染混沌信號的降噪算法.所設計的降噪算法通過對相似片段的分組將一維混沌信號的降噪轉化為一個二維聯合濾波問題;然后,在二維變換域用閾值法衰減噪聲;最后,通過反變換獲得原始信號的估計.由于分組中的相似片段具有良好的相關性,與直接在一維變換域做閾值降噪相比,分組的二維變換能獲得原信號更稀疏的表示,更好地抑制噪聲.仿真結果表明,該算法對原始混沌信號的重構精度和信噪比的提升都優于小波閾值、局部曲線擬合等現有的混沌信號降噪方法,對相圖的還原質量也更好.

10.7498/aps.66.210501

?國家自然科學基金(批準號:61372008)和廣東省科技計劃項目(批準號:2015B010101006,2014A010103014)資助的課題.

?通信作者.E-mail:liuxy@scut.edu.cn

?2017中國物理學會Chinese Physical Society