側風作用下高速列車的空氣動力學初探

成 楠， 張明祿

(西南交通大學力學與工程學院， 四川成都 610031)

側風作用下高速列車的空氣動力學初探

成 楠， 張明祿

(西南交通大學力學與工程學院， 四川成都 610031)

用大渦模擬(LES)計算側風影響下的簡化了的高速列車環流。文章基于列車高度和來流速度，確定流動的雷諾數Re為5.5×108。在偏轉角(在相對的側風方向和列車前進方向的夾角)為90°情況下，獲得計算結果。通過大渦模擬( LES)數值計算方法，對均勻定常側風下高速列車的非定常空氣動力特性進行了研究。計算結果分析表明，即使在均勻定常側風下，列車所受空氣動力也存在明顯的非定常性。

高速列車； 側風； 氣動力； 非定常

由于高速列車不斷升高的速度，高速列車遭受的空氣動力問題越顯突出[1]。列車行駛安全性與舒適性均和列車側風問題有關，在眾多列車空氣動力問題中，列車側風是一個重要問題。從世界范圍來看，由于側風引發的列車事故屢見不鮮，2007年，新疆一列車受大風影響導致出軌，造成了嚴重交通事故[2]。高速鐵路發展的趨勢是列車車體輕量化和行駛高速化，但與此同時，這種發展趨勢也會使側風導致列車傾覆的概率明顯增加[3]。

為了提高在側風下列車行駛的安全性，近幾十年國內外研究人員進行了大量研究，包括通過風洞試驗、實車試驗及數值計算等方法，考察了列車在側風下的空氣動力特性[4-7]。但這些研究的主要結論是在側風下對列車的定常(時間平均)空氣動力特性以及列車運行穩定性受側風風速波動的影響，而從最近幾年才開始對列車在側風下的瞬時流場以及列車所受空氣動力的瞬時特性的研究。2004 年，Christina Rol n等人發表論文指出，在較大側風偏轉角情況下，列車的空氣動力具有很強的非定常特點[3]; 2005年～ 2006年，Hassan Hemida 發表多篇論文[8-9]并根據計算結果指出，在側風作用下列車所受的非定常空氣動力的頻率接近真實列車系統的固有頻率。國內尚未見到關于列車在側風下非定常空氣動力方面的研究的相關文獻。通過以上分析可以看出，在側風下列車非定常空氣動力特性的研究還未有系統的研究，尚屬起步階段。同時，已有部分研究結果指出，側風作用在列車上的定常空氣動力的大小不足以解釋列車被大風吹翻的原因[11]。因此，研究側風下列車非定常空氣動力問題具有現實意義。

針對自然風速相對列車的偏轉角為 90°的情況，本文通過大渦模擬(LES)數值計算方法，研究了車身所受空氣動力的非定常特性以及列車周圍非定常流場特性，最后根據研究結果，為列車側風非定常空氣動力特性提出了筆者的看法。

1 數值模型和計算方法

1.1 數值模型

為了將問題簡化，同時突出所研究的側風部分，本文研究是在自然風速的偏轉角為 90°的情況，即風向為橫向垂直于高速列車側壁，且不考慮列車行駛方向的速度。側風角和偏轉角定義方式如圖1所示。本次計算采用的實車模型是CRH2型高速列車，為減少計算量和計算時間，采取如下簡化：(1)將列車分為頭車、中間車和尾車，分別設為25.5 m、25 m和25.5 m，整輛列車為一連續剛體。(2)將列車表面簡化成光滑曲面，認為表面的粗糙度各處一致，并假設表面摩擦力沿車身均勻分布。(3)在實際模擬計算中把列車底部的復雜結構去掉,使列車底面和地面間形成了一個狹縫，并用這個狹縫對流場的影響來模擬列車底部結構對流場的影響，本文中列車與地面間距設為0.2 m。

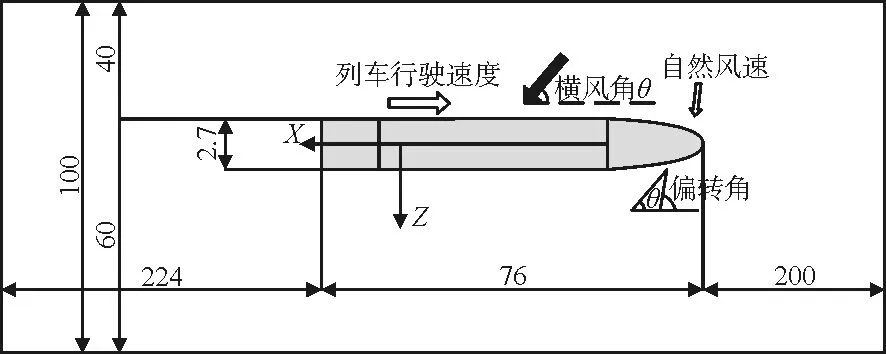
圖1 列車與計算流域位置(單位:m)

1.2 計算域設定及網格劃分

(1) 計算域。 將計算域劃分為來流區和尾流區，根據繞流流場的基本特性，尾流區域取較大值。列車模型尾流區域的縱向長度大于3倍的列車模型總長度，列車模型前端的流場區域的縱向長度大于2倍的列車模型寬度，計算域高度大于10倍的車高[2]。計算域的幾何尺寸為 500 m×40 m×100 m(圖1)。

(2) 網格劃分。采用非結構化網格，共生成500多萬。為了保證網格質量，提高壁面函數應用于邊界層模擬的準確性網格，在車體表面及地面處生成邊界層網格，邊界層網格的厚度為100 mm，增長比為1.2，共設置5層邊界層網格。

1.3 邊界條件

模擬列車附近的外流場采用相對運動條件。即假定列車靜止，空氣來流以與列車運行速度反向等值的速度vt繞流列車，側風以速度vw吹向列車，二者的合成速度為v(圖1)。

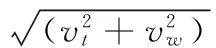
(2)出口邊界條件。壓力邊界條件，出口壓力取一個標準大氣壓強。

(3)計算域表面。由于選擇的流場計算區域足夠大，可認為外圍邊界對列車周圍的流場的影響甚小，計算區域的外圍邊界設定為壓力出口。

2 計算結果及其分析

列車速度vt= 350 km/h，側風速度vw=30 m/s，側風的偏轉角為90°的列車表面壓力分布。

從迎風側靜止壓力圖，可以看出頭車前緣的正負壓最大，其他位置不是危險截面(圖2)。我們需要重視危險位置，把重要問題突出。其中負壓比正壓系數要多出50 %，因此列車在側風下的行駛過程中，更可能被吸走，而不是吹走。

圖2 靜止壓力和列車位置的關系

本研究將計算初始時間的部分刪除，留下穩定計算結果，得出時間-側力曲線圖(圖3)。

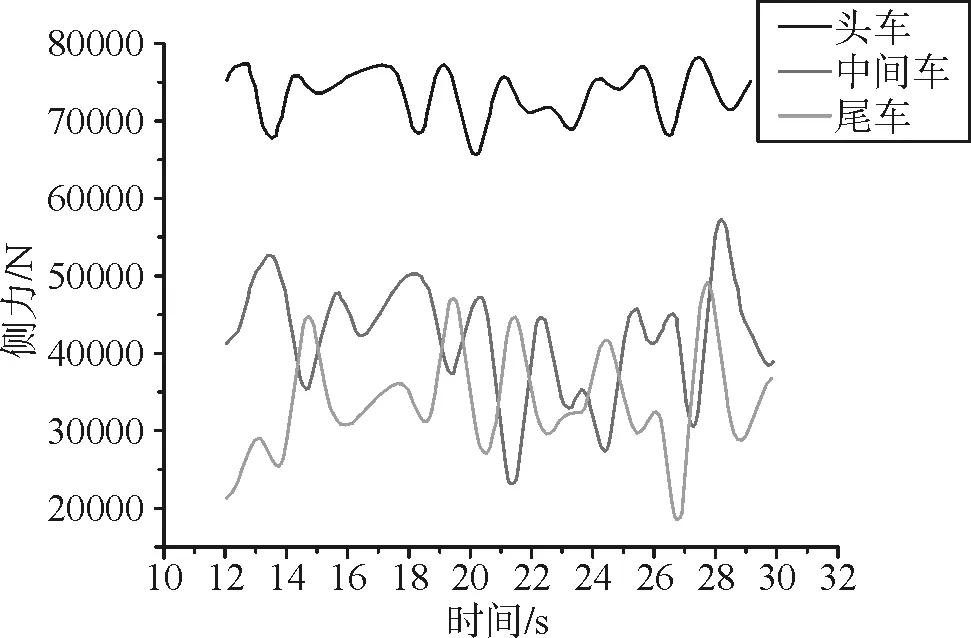
圖3 頭車、中間車和尾車的側力值隨時間的變化曲線

列車表面壓力分布是在總體趨勢不變的情況下, 隨時間在均值附近波動, 這種波動的幅值及相應位置存在隨機性。這種壓力波動表明: 即使在定常側風的情況下, 列車所受空氣動力也存在明顯的非定常性。由圖3可以看出在側風作用下，三個不同位置頭車的側力峰值最大，而且無論是幅值還是變化程度，中間車和尾車都相對頭車較小，因此最應當受到關注的位置是頭車。

而后，又采用了不同車速、風速和偏轉角，依然得到相似的氣動力幅值與列車位置的規律。

3 結論

本文基于計算流體力學和多體動力學仿真技術，對側風下高速列車的空氣動力學特征進行了數值模擬，可得到如下結論：

(1)受到極大關注的側力在頭車位置最為危險，接下來的研究應當集中關注頭車的氣動力情況。而在頭車前緣的位置，壓力系數最大，因此考慮最大受力位置時，頭車的位置應當是首當其沖的。

(2)列車所受非定常力是由于側風導致的非定常流場產生，并且列車所受非定常空氣動力特性與其周圍非定常流場特性之間存在對應關系。因此，有可能在風洞試驗中，通過對列車周圍非定常流場的測量得到列車在側風下所受非定常空氣動力特性。

[1] Raghu S Raghunathana, Kim H D, Setoguchi T. Aerodynamics of highspeed railway train [J] . Progress in Aerospace Sciences, 2002, 38: 469-514.

[2] 王麗麗. 新疆步入高鐵時代[J]. 大陸橋視野, 2014(11):26-30.

[3] Christina Rol n, Thomas Rung, Don Wu. Computational modeling of crosswind stability of highspeed trains[DB/OL]. ECCOMAS 2004.

[4] 王厚雄, 林榮生. 列車的側風傾覆力矩特性[J] . 空氣動力學學報, 1983, 1(3) :72-77.

[5] 高廣軍, 田紅旗, 姚松, 等. 蘭新線強側風對車輛傾覆穩定性的影響[J] . 鐵道學報, 2004, 26(4): 36-40.

[6] Cooper K. Effect of crosswinds on trains[J] . Journal of Fluids Engineering, Transactions of the ASME, 1981, 103(1): 170-178.

[7] C J Baker, J Jones, F LopezCalleja, J Munday. Measurements of the cross wind forces on trains [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2004, 92(7): 547-563.

[8] Hassan Hemida, Sinisa Krajnovic, Lars Davidson. Large eddy simulation of the flow around a simplified high speed train under the influence of a crosswind [C]//AIAA .17 th AIAA Computational Fluid Dynamics Conference2005, AIAA 2005-5354.

[9] Hassan Hemida, Sinisa Krajnovic. Numerical study of the unsteady flow structures around trainshaped body subjected to side winds [DB/OL] . ECCOMAS CFD 2006.

[10] 王兆軍, 張軍, 朱春華, 等. 南疆列車傾覆事故的動力學因素分析[J]. 力學與實踐, 2007, 29(5) : 87-89.

[11] Lilly K. A Proposed Modification of the Germano Subgrid Scale Closure Model[ J] . Physics of Fluids, 1992, 4(3) :633-635.

[12] 陶文銓. 數值傳熱學[M]. 2 版. 西安:西安交通大學出版社, 2005:218-226.

U260.11

A

[定稿日期]2017-05-05

成楠(1991～)，男，碩士，研究方向為高速列車空氣動力學。