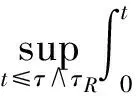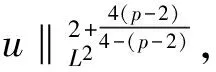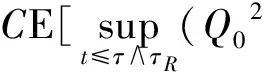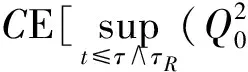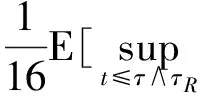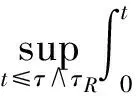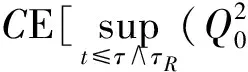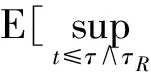帶非齊次Dirichlet邊界的隨機非線性Schr?dinger方程解的整體存在性

謝靈燕, 陳光淦

(四川師范大學 數學與軟件科學學院, 四川 成都 610066)

帶非齊次Dirichlet邊界的隨機非線性Schr?dinger方程解的整體存在性

謝靈燕, 陳光淦*

(四川師范大學 數學與軟件科學學院, 四川 成都 610066)

研究帶有非齊次Dirichlet邊界條件且帶有加性白噪聲的隨機非線性Schr?dinger方程在H1(R+)空間中的整體解存在性.在偏微分方程理論、泛函分析和隨機分析等知識基礎上,在質量泛函和能量泛函的基礎上引入第三個“橋梁”泛函,通過It公式建立3個泛函之間的關系,最終獲得帶非齊次Dirichlet邊界的隨機非線性Schr?dinger方程在具有競爭非線性的各種情況下解的有界性,從而獲得方程的解的整體存在性.

隨機非線性Schr?dinger方程; 非齊次Dirichlet邊界條件; 加性白噪聲; 整體存在性

近年來非線性Schr?dinger方程廣泛地應用在量子力學、光學、物理、電磁等多個領域中.對于非線性Schr?dinger方程,非線性項會影響到解的適定性以及解的爆破行為.目前,非線性Schr?dinger方程方面的研究非常多[1-9].隨機非線性Schr?dinger方程描述光或者波在隨機介質中的傳播過程,這個過程和時間相關,并且光或者波在傳播的過程中會受到不確定因素的干擾.

本文研究同時具有噪聲和非齊次的邊界條件的非線性Schr?dinger方程的整體解,因此,考慮一類帶非齊次Dirichlet邊界且具有加性白噪聲的隨機非線性Schr?dinger方程

iut=uxx+k|u|p-2u+

x∈R+,t≥0,

(1)

賦予非齊次Dirichlet邊界條件

u(0,t)=Q(t),t≥0,

(2)

初值為

u(x,0)=u0(x),

x∈R+,

(3)

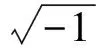
對于帶非齊次Dirichlet邊界條件的非線性Schr?dinger方程的研究,文獻[10-11]給出了方程的局部適定性、解的整體存在性以及有限時間內爆破,但此方法不適用于帶非齊次Dirichlet邊界條件的隨機非線性Schr?dinger方程相關的問題.對于帶齊次邊界條件的隨機非線性Schr?dinger方程,文獻[12-13]獲得了具有加性噪聲或者乘性噪聲的系統的局部適定性、解的整體存在性以及爆破,但他們的方法仍然不適用于帶非齊次Dirichlet邊界條件的隨機非線性Schr?dinger方程.

本文研究非齊次Dirichlet邊界和白噪聲同時對非線性Schr?dinger方程的影響.為了克服非齊次邊界條件和白噪聲同時給方程帶來的困難,運用偏微分方程理論、泛函分析和隨機分析的相關知識,詳細地分析系統的特征,在質量泛函和能量泛函的基礎上引入第三個“橋梁”泛函,通過It公式建立3個泛函之間的關系,最終獲得帶非齊次Dirichlet邊界的隨機非線性Schr?dinger方程在具有競爭非線性的各種情況下解的有界性,從而獲得方程的解的整體存在性.

1 預備知識

設(Ω,F,P)是一個完備的概率樣本空間,并賦予一個域流(Ft)t≥0,另外定義由相互獨立的實值布朗運動組成的序列(βe)e∈N,相關于域流(Ft)t≥0,賦予1個希爾伯特正交基(ee)e∈N∈L2(R+),φ∈L2(R+)是有界線性算子.關于W這個維納過程有

t≥0,x∈R+,ω∈Ω,

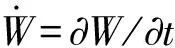
y.

此噪聲的相關函數為

其中

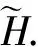
其中(ee)e∈N是空間H上的任意標準正交基.

[14]-[15],有如下局部適定性.

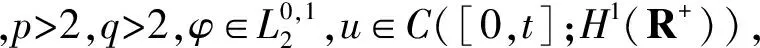
τ*(u0,ω)=+∞,

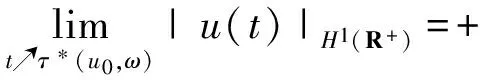
2 系統的特征分析

現在定義3個泛函,質量泛函

能量泛函

▽u(x)|2dx-

第三個泛函

x.

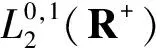
M(u(t))=M(u0)-

(4)

證明對M(u)運用It公式得

M(u(t))=M(u0)+

iλ|u|q-2u)ds+

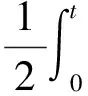
(5)

其中Mu(u)h是一階Fréchet微分,h∈H,H是一個Hilbert空間,計算可得

x.

Muu(u)(h1,h2)是二階Fréchet微分,h1,h2∈H,H是一個Hilbert空間,計算可得

x.

進一步可得:

(6)

ik|u|p-2-iλ|u|q-2u)ds=

(7)

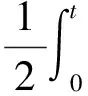
(8)

將(6)～(8)式代入(5)式可得(4)式.

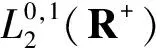
λ|u|q-2u)φee(x)dxdβe(s)-

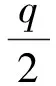
(9)

證明對H(u)運用It公式得

iλ|u|q-2u)ds+

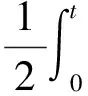
(10)

Hu(u)h是一階Fréchet微分,h∈H,H是一個Hilbert空間,計算可得

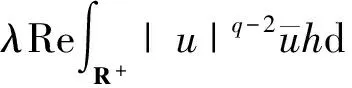
Huu(u)(h1,h2)是二階Fréchet微分,h1,h2∈H,H是一個Hilbert空間,計算可得

進一步可得:

(11)

iλ|u|q-2u)ds=

(12)

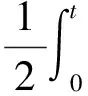
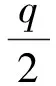
(13)

將(11)～(13)式代入(10)式可得(9)式.

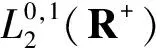
(14)

證明同樣用It公式計算得到

ik|u|p-2-iλ|u|q-2u)ds+

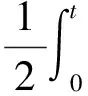
(15)

其中Iu(u)h是一階Fréchet微分,h∈H,H是一個Hilbert空間,可得

其中Iuu(u)(h1,h2)是二階Fréchet微分,h1,h2∈H,H是一個Hilbert空間,可得

Iuu(u)(h1,h2)=

進一步得:

(16)

ik|u|p-2-iλ|u|q-2u)ds=

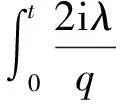
(17)

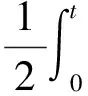
(18)

將(16)～(18)式代入(15)式可得(14)式.

3 系統的解的整體存在性

3.1非線性項系數k=1,λ=1時方程的解的整體存在性

則方程(1)的解整體存在.

證明令

通常習慣用C表示常數.對任給的T0>0,任給停時τ

τR=inf{t≤τ*(u0),‖u(t)‖H1(R+)≥R}.

由(14)式得

(19)

對以上等式兩邊同時取期望,通過H?lder不等式和BDG不等式等工具的處理可得

還可得

‖u(t)‖2]≤

(21)

當k=1,λ=1時,有

▽u(x)|2dx-

對H(u)兩邊同時估計期望,化簡得

‖ux‖2]≤

(22)

(23)

由(20)～(23)式,運用Young不等式可得

‖ux‖2]≤E(H(u0))+

(24)

將(21)式代入(24)式得

‖ux‖2]≤E(H(u0))+

(25)

3.2非線性項系數k=1,λ=-1時方程的解的整體存在性

則方程(1)的解整體存在.

證明令

對任給的T0>0,任給停時τ

τR=inf {t≤τ*(u0),‖u(t)‖H1(R+)≥R}.

當k=1,λ=-1有

▽u(x)|2dx-

對H(u)兩邊同時估計期望可得

‖ux‖2]≤E(H(u0))+

(26)

由Gagliardo-Nirenberg和Young不等式可得

(27)

將(20)、(21)和(27)式代入(26)式得

‖ux‖2]≤E(H(u0))+

(28)

在(20)和(21)式的基礎上,運用Young不等式可得

‖ux‖2]≤E(H(u0))+

(29)

3.3非線性項系數k=-1,λ=-1時方程的解的整體存在性

則方程(1)的解整體存在.

證明令

對任給的T0>0,任給停時τ

τR=inf{t≤τ*(u0),‖u(t)‖H1(R+)≥R}.

當k=-1,λ=-1時有

▽u(x)|2dx+

對H(u)兩邊同時估計期望得

‖ux‖2]≤E(H(u0))+

(30)

在(20)和(21)式基礎上,對(30)式用Young不等式進一步計算有

‖ux‖2]≤E(H(u0))+

(31)

參考文獻

[1] UEDA T, KATH W L. Dynamics of optical pulses in randomly birefrengent fibers[J]. Physica D Nonlinear Phenomena,1992,55(1/2):166-181.

[2] CHEN G G, ZHANG J. Remark on global existence for the superctitical nonlinear Schr?dinger equation with a harmonic potential[J]. J Math Anal Appl,2006,320(4):591-598

[3] CHEN G G, DUAN J Q, ZHANG J. Geometric shape of invariant manifolds for a class of stochastic partial differential equations[J]. J Math Phys,2011,52(7):072702.

[4] 舒級,張健. 一類帶無界勢的非線性Schr?dinger方程的整體性[J]. 四川師范大學學報(自然科學版),2005,28(4):20-22.

[5] 步起躍. 半無窮直線上的非線性薛定諤方程[J]. 數學年刊,2000,21(4):437-448.

[6] CARROL R, BU Q Y. Solution of the forced nonlinear Schr?dinger equation using PDE techniques[J]. Appl Anal,1991,41(1):33-51.

[7] BRZEZNIAK Z, PESZAT S. Space-time continuous solutions to SPDE’s driven by a homogeneous Wiener process[J]. Studia Math,1999,123(1):261-299.

[8] BOUARD D A, DEBUSSCHE A. A Finite time blow-up in the additive supercritical stochastic nonlinear Schr?dinger euqation:the real noise case[J]. Contemp Math,2002,301(4):183-194.

[9] BANG O, CHRISTIANSEN P L. White noise in the two-dimensional nonlinear Schr?dinger euqation[J]. Appl Anal,1995,57(7):3-15.

[10] BU C. Forced cubic Schr?dinger equation with Robin boundary data:continuous dependency result[J]. ANZIAM J,2000,41(3):301-311.

[11] GUO B L, WU Y H. Global existence and nonexistence of the solution of a forced nonlinear Schr?dinger equation[J]. I Math Phys,1995,36(7):3479-3483.

[12] BOUARD D A, DEBUSSCHE A. The stochastic nonlinear Schr?dinger equation inH1(Rn)[J]. Stochastic Anal Appl,2003,21(5):97-126.

[13] BOUARD D A, DEBUSSCHE A. On the effect of a noise on the solutions of the focusing supercritical nonlinear Schr?dinger Equations[J]. Probab Theory Related Fields,2002,123(1):76-96.

[14] BU Q. On well-posedenss of the forced NLS equation[J]. Appl Anal,1992,46(1):219-239.

[15] STRAUSS W. An inhomogeneous boundary value problem for nonlinear Schr?dinger equation[J]. J Diff Eqns,2001,173(1):79-91.

Global Existence of a Stochastic Nonlinear Schr?dinger Equation with Inhomogeneous Dirichlet Boundary Value

XIE Lingyan, CHEN Guanggan

(CollegeofMathematicsandSoftwareScience,SichuanNormalUniversity,Chengdu610066,Sichuan)

We study the global existence of solutions in the energy spaceH1(R+) for the stochastic nonlinear Schr?dinger equation with Dirichlet boundary value. Based on the partial differential equations theories, functional analysis and stochastic analysis, we introduce the third bridge functional on the basis of quality functional and energy functional and establish the relationship among these three functionals by Itformula. We get the boundedness of the solution of the the stochastic nonlinear Schr?dinger equation with inhomogeneous Dirichlet boundary value, additive white noise and competitive nonlinear terms in each cases and finally obtain the global existence of solution of the equation.

stochastic nonlinear Schr?dinger equation; inhomogeneous Dirichlet boundary value; white noise; global existence

2015-04-08

國家自然科學基金(11347102)和四川省杰出青年帶頭人培育計劃基金(2012JQ0041)

*通信作者簡介：陳光淦(1978—),男,教授,主要從事隨機偏微分方程的研究,E-mail:chenguanggan@hotmail.com

O159

A

1001-8395(2017)05-0593-07

10.3969/j.issn.1001-8395.2017.05.005

2010MSC：60H15; 35L05; 60H30

(編輯 鄭月蓉)