繃緊式系泊纜沖擊張力特性研究

張火明，謝 卓，方貴盛，孔令濱

(1.中國計量大學 浙江流量計量技術重點實驗室，浙江 杭州 310018; 2.浙江水利水電學院 機械與汽車工程學院，浙江 杭州 310018)

繃緊式系泊纜沖擊張力特性研究

張火明1，謝 卓1，方貴盛2，孔令濱1

(1.中國計量大學 浙江流量計量技術重點實驗室，浙江 杭州 310018; 2.浙江水利水電學院 機械與汽車工程學院，浙江 杭州 310018)

采用集中質量法研究了繃緊式系泊系統中系纜由于松弛-張緊過程產生的沖擊張力。建立系泊纜繩離散的集中質量模型，對其獨立單元進行受力分析并建立了單元的運動方程。給定纜繩上端點簡諧激勵，通過Ansys中的Aqwa模塊，分析了纜繩的運動響應；針對纜繩運動響應過程中的三種狀態進行了模擬計算，探討了沖擊張力產生的條件；研究了纜繩初始預張力、上端點激勵幅值和頻率、拖曳力系數、彈性模量以及單位長度質量對動態張力的影響。研究結果表明：這些影響因素不僅會影響纜繩動態張力的大小，也會對纜繩中的沖擊張力產生一定的影響。

繃緊式系泊纜；運動響應；沖擊張力

近年來，新型繃緊式系泊系統憑借其在深水應用中的優越表現而倍受關注。在系泊系統運動響應過程中，當浮體運動幅值超過某一臨界值時，纜繩可能會表現出零張力和最大值張力，即出現了纜繩沖擊現象。纜繩發生沖擊現象時產生的力通常比簡單的動態載荷大很多，這會對纜索結構造成很大的破壞，嚴重影響系泊系統的使用壽命。因此對系泊纜繩沖擊張力特性的研究就顯得十分重要。

Plaut等[1-2]研究發現當浮體的運動幅度很大時，纜繩就會松弛，一旦再次張緊，就會出現很大的動態張力，此時能量會有損失。Dracos和Huang[3]通過試驗研究發現纜繩在張緊狀態時，張力以激振頻率變化，但是一旦發生松弛-張緊現象，就會在張力中出現高頻分量。Huang[4]通過研究發現，纜繩在松弛狀態下，會發生幾何形狀的改變；張緊狀態，纜繩則表現出單純的彈性載荷模式；松弛-張緊狀態，纜繩跨越了從幾何構型到彈性變形的過程。劉敏[5]以簡化的系泊系統力學模型為對象，研究了在激振力不同初始條件下系泊纜繩的非線性動力學特性。趙景瑞[6]依據集中質量法建立系泊纜繩柔性力學模型，研究了各種因素對于纜繩動態張力與水中構型的影響程度。唐友剛[7]考慮到纜繩所具有的粘-彈特性，對深海平臺系泊系統松弛-張緊引起的沖擊載荷進行了研究。張素俠[8]采用應力波的方法對深海系泊系統松弛-張緊過程的沖擊張力進行了研究。曹陽，張素俠等[9-10]對系泊纜繩的沖擊載荷進行了實驗研究，通過對比分析的方法，研究了不同因素對纜繩張力帶來的影響并探討了纜繩發生沖擊張力的判別方法。研究后得出沖擊載荷發生的重要特征為：歷程張力曲線變得陡峭、張力值急劇增大以及張力中出現多倍響應頻率成分。

本文借助Ansys中的Aqwa模塊，針對纜繩運動響應過程中的三種狀態進行了模擬計算；研究了纜繩初始預張力、上端點激勵幅值和頻率、拖曳力系數以及彈性模量對動態張力的影響。

1 數值模擬

1.1模型建立

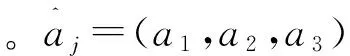
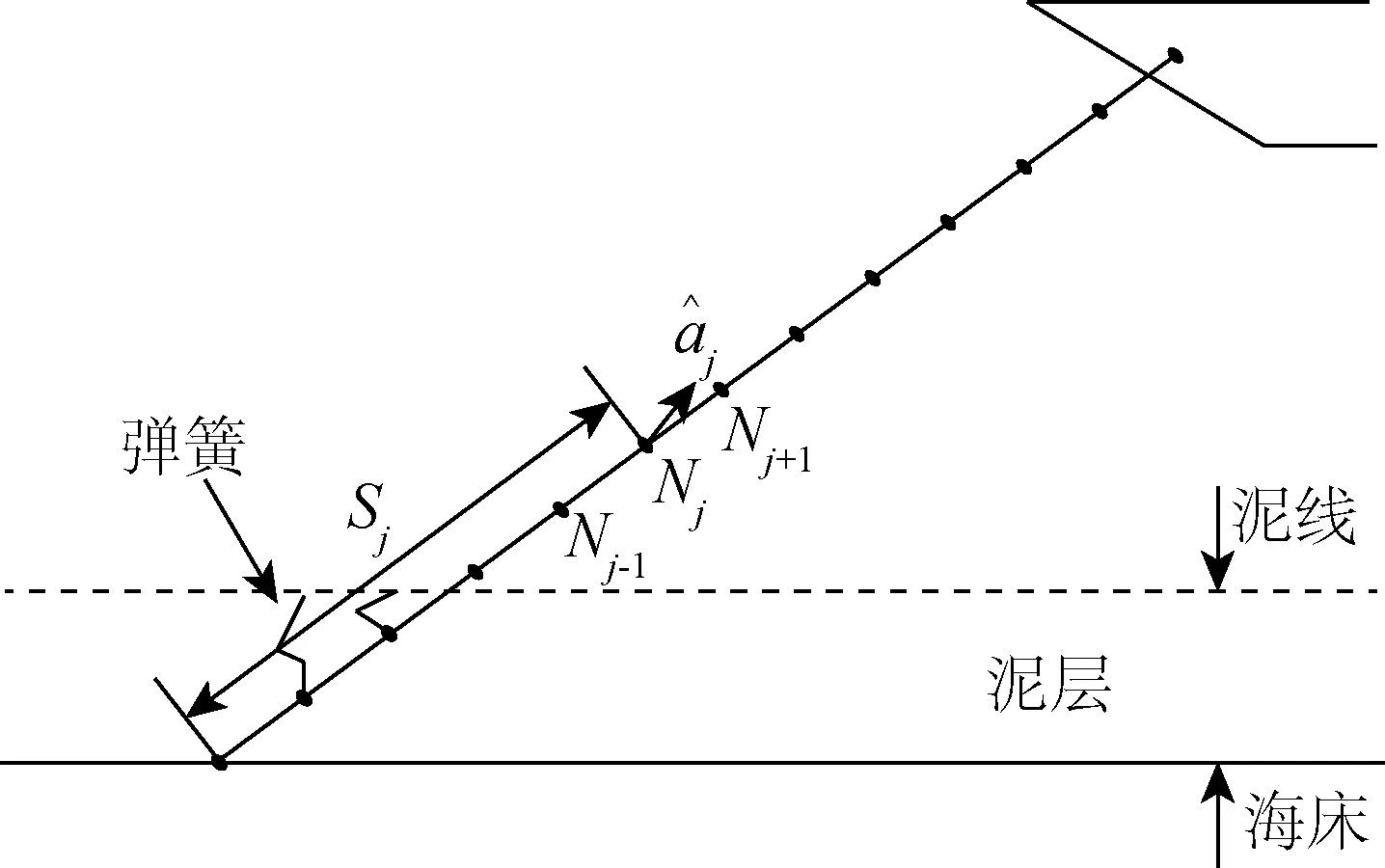
圖1 纜繩離散集中質量模型Fig.1 Discrete mass model of the cable

圖2 纜繩單元受力分析Fig.2 Force analysis of cable

1.2運動方程

圖2顯示了細長圓環型纜繩單元的受力情況。作用于纜繩單元的外力主要包括流體水動力載荷以及慣性載荷。在纜繩動態分析中不考慮扭轉變形。此纜繩單元的運動方程如下：

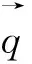
纜繩的彎矩和張力分別與其彎曲剛度和軸向剛度有關，其關系如下：

式中：I為截面關于中性軸的慣性矩，ε為單元軸向應力。

為確保方程(1)～(4)的唯一解，在頂部和底部兩端施加固定的連接邊界條件：

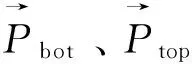
為了求解纜繩速度和位置的估計加速度值，采用兩階段預測-校正算法。第一階段為預測階段，首先要計算出總的作用力，往往是已知時間、位置、速度的函數；然后對在t+dt時刻的速度和位置進行預測。第二階段為校正階段，求出在t+dt時刻的總作用力值以及加速度值；利用泰勒定理計算t+dt時刻修正后的速度和位置。

2 纜繩動力響應結果及分析

選取的纜繩參數如表1所示。

表1 纜繩參數表Tab.1 Parameters of cable

2.1纜繩運動響應分析

纜繩參數如表1所示，給定纜繩上端點激勵為正弦激勵，激勵幅值Ap=5 m，激勵頻率f=1 rad/s，設定錨系點為坐標原點，沿纜繩方向為正方向，選取纜繩500 m和1 500 m處，對其進行計算，得到不同方向的時域位移歷程曲線以及運動軌跡曲線，如圖3和圖4所示。

圖3 纜繩1 500 m處運動軌跡Fig.3 The trajectories of cable at 1 500 m

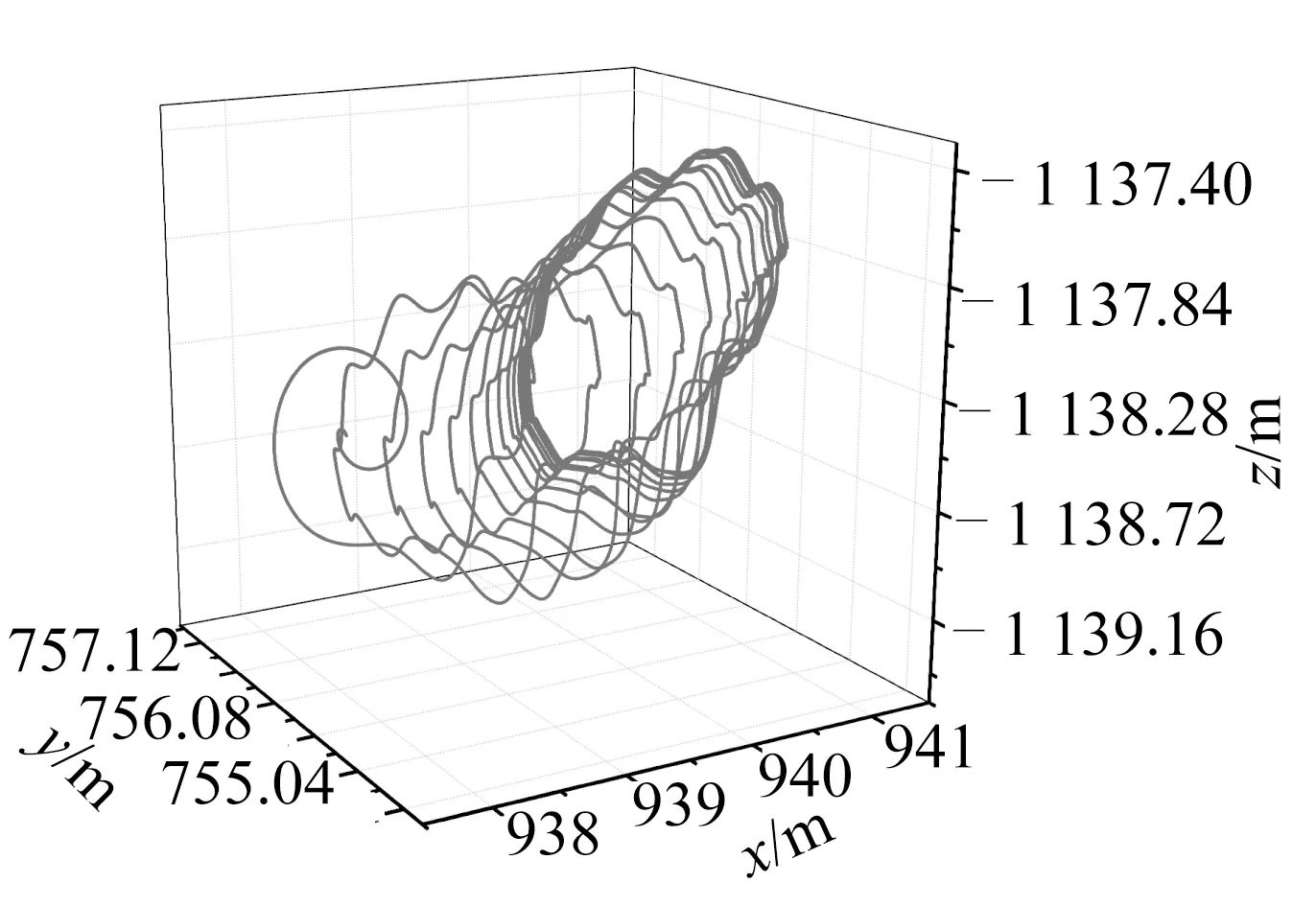
圖4 纜繩500 m處運動軌跡Fig.4 The trajectories of cable at 500 m

從圖3和圖4中可以看到，雖然纜繩上端點僅僅是沿x軸方向進行激勵，但是纜繩在x軸，y軸，z軸方向均產生運動響應，且纜繩初期的運動軌跡分布比較松散，這說明初期運動不穩定；但經過一段時間后，運動軌跡逐漸趨于密集甚至重合，這說明纜繩運動會達到穩定狀態，最終將沿某一特定軌跡運動。

2.2纜繩張力分布

纜繩的最大張力值對纜繩的研究具有重要意義，對纜繩各部分的張力值進行計算，以確定各段纜繩的張力情況。取纜繩質量為89.43 kg/m，上端激勵幅值為5 m，激勵頻率為1 rad/s。對100 s內纜繩各段張力進行計算，得到各段纜繩張力的最大值如圖5所示。從圖中可以看出，纜繩兩端的張力最大值較大，其中頂端略大于底部張力值，中間部分較小， 在1 000 m左右達到最小值。

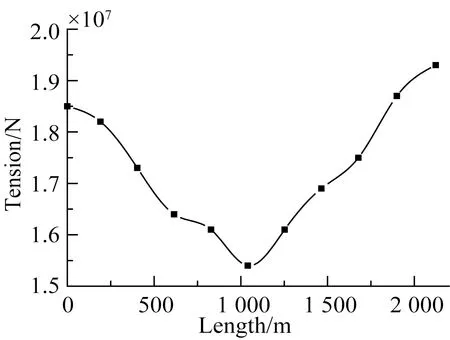
圖5 纜繩前100 s各段張力最大值Fig.5 The maximum value of the tension

3 纜繩沖擊張力特性研究

3.1沖擊張力產生條件

纜繩的運動過程分為三種狀態，分別是：松弛狀態，松弛-張緊狀態和張緊狀態。為研究沖擊張力產生條件，分別針對三種狀態下纜繩的動態張力進行研究。纜繩錨系點以及上端導纜點固定，固定距離為2 123 m。文中通過改變設置纜繩的長度，以達到纜繩在三種狀態下運動的條件。

1)松弛狀態下纜繩動態張力

設置纜繩長度為2 140 m，此時纜繩初始預張力為1.561E6 N，給定上端點激勵幅值為0.5 m，分別采用線性方法和非線性方法進行計算，其中非線性方法主要考慮非線性剛度，得到纜繩的線性和非線性張力如圖6所示。從圖6中可以觀察到，纜繩的非線性張力要稍大于線性張力。動態張力曲線隨時間呈正弦曲線變化，過程中并沒有沖擊張力的產生。

圖6 松弛狀態纜繩張力曲線Fig.6 The cable tension curve in the relaxed state

圖7 張緊狀態纜繩張力曲線Fig.7 The cable tension curve in the tightened state

2)張緊狀態下纜繩動態張力

設置纜繩長度為2 120 m，此時纜繩處于繃緊狀態，纜繩初始預張力為6.524E6 N，給定纜繩上端點激勵幅值為2 m，纜繩運動過程中將一直處于繃緊狀態。計算得到纜繩的線性和非線性動態張力曲線如圖7所示。從兩條曲線對比可以看出，在張緊狀態下，除前10 s，兩種方法計算得到的動態張力曲線基本重合。

3)松弛-張緊狀態纜繩動態張力

參數如同張緊狀態時，增大上端點激勵幅值，纜繩運動過程中將會經歷松弛-張緊狀態。采用線性與非線性方法計算得到纜繩的動態張力曲線如圖8所示。采用非線性方法計算得到的動態張力曲線中，出現了許多突變的尖峰，且不同于松弛和張緊狀態，張力中出現負張力值。與線性張力曲線相比，非線性張力的峰值要遠大于線性張力的峰值。圖9為線性和非線性張力的頻率成分圖。張力的頻率成分中除了激勵頻率f=1.0 rad/s成分外，還出現了f=2.0、3.0、4.0、5.0和6.0 rad/s的頻率成分，由此可知系統內可能發生了2倍、3倍、4倍甚至5倍的超諧共振。

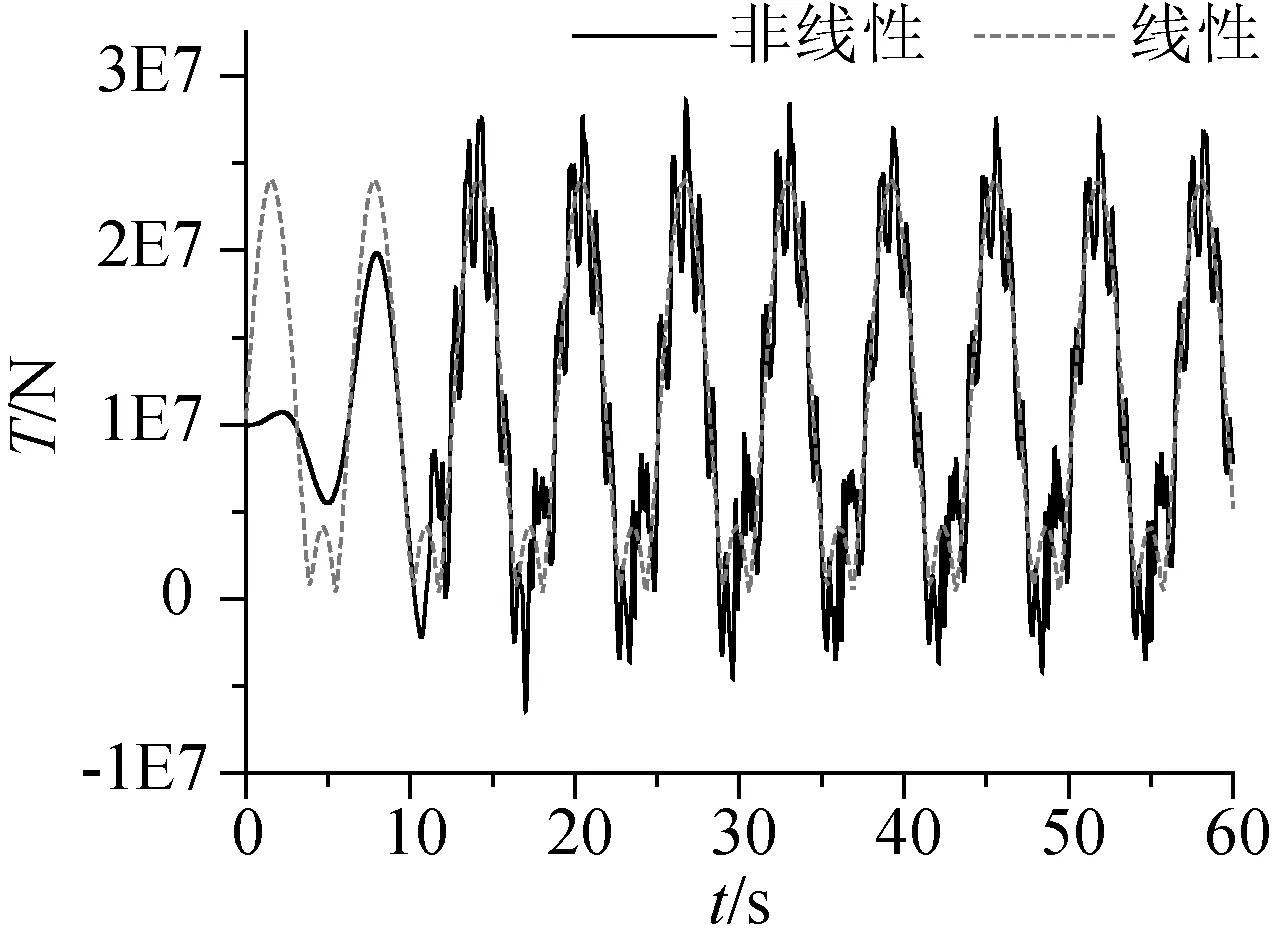
圖8 線性和非線性動態張力曲線Fig.8 Linear and nonlinear dynamic tension curve

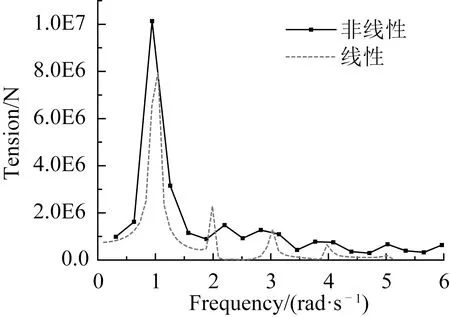
圖9 頻率成分Fig.9 Frequency component diagram

3.2不同因素對纜繩動態張力影響

1)初始預張力對纜繩動態張力影響

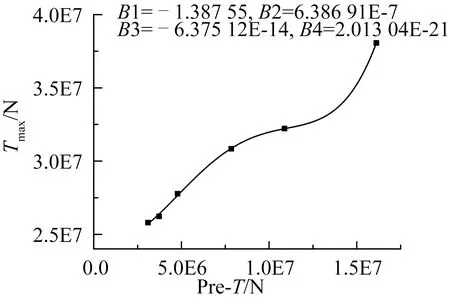
圖10 初始預張力與動態張力關系Fig.10 The relation between pre-tension and dynamic tension

取激勵幅值A=10 m，激勵頻率f=1 rad/s，纜繩彈性模量E=1E9 N/m2，計算得到纜繩動態張力與初始預張力曲線，采用四階多項式進行擬合，擬合系數分別為：B1=-1.387 55，B2=6.386 91E-7，B3=-6.375 12E-14，B4=2.013 04E-21，如圖10所示。纜繩的動態張力與預張力的關系曲線呈非線性上升趨勢，隨著預張力的增大，纜繩的張力最大值也逐漸增大。

2)拖曳阻力系數對纜繩張力影響

在纜繩的運動方程中，流體產生的拖曳力，是造成系統非線性的主要因素之一。研究流體拖曳力對纜繩動態張力的影響，取上端點激勵幅值Ap=5 m，頻率f=1 rad/s，縱向拖曳力系數Cd2=0.025。

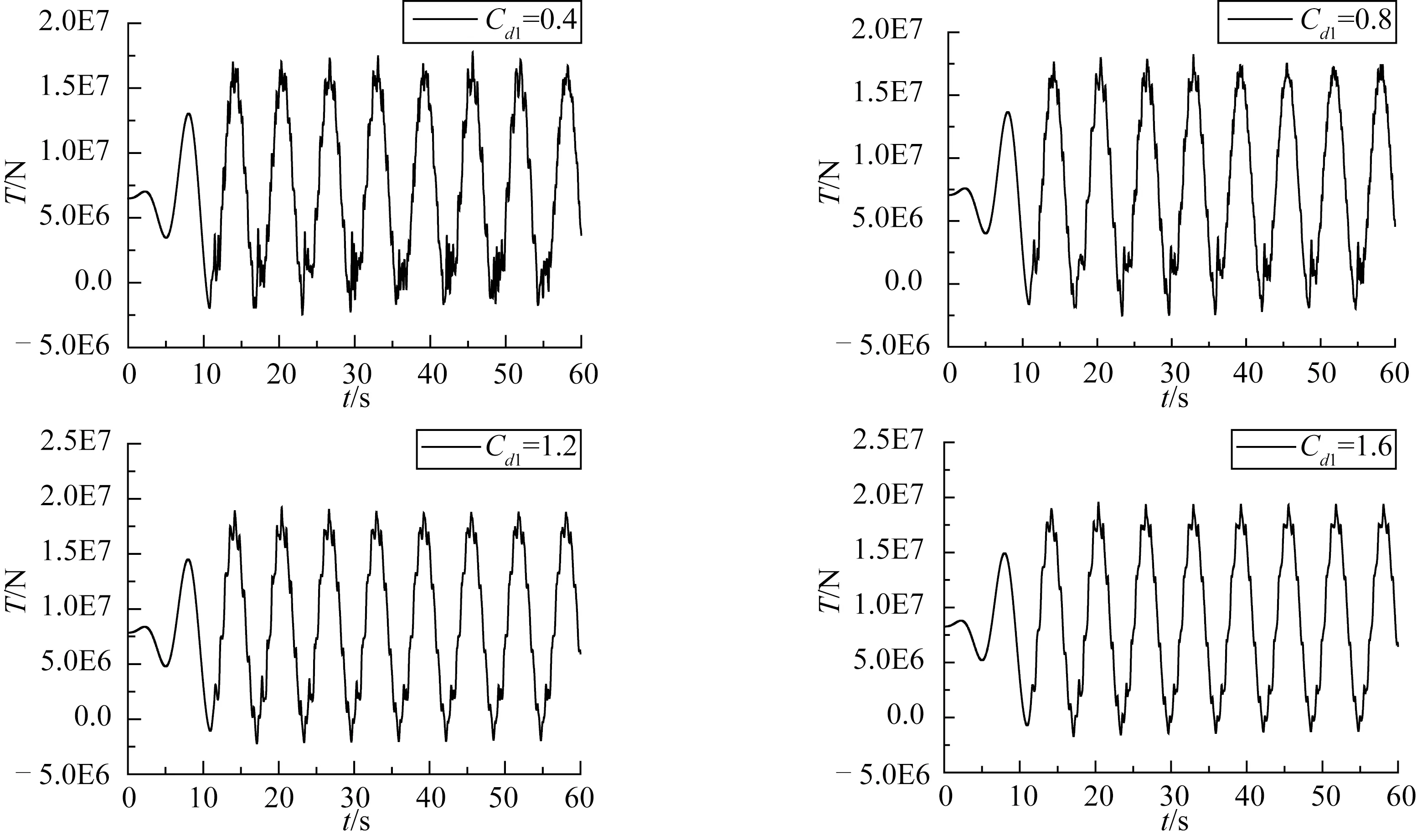
圖11 不同橫向阻尼纜繩動態張力曲線Fig.11 The dynamic tension curves of different transverse drag coefficients

計算不同橫向拖曳力系數時，纜繩動態張力曲線如圖11所示，圖12是橫向阻尼與纜繩張力最大值的四階擬合曲線，擬合系數分別為B1=-8.931 82E6，B2=1.512 02E7，B3=-8.282 34E6，B4=1.475 09E6。

從圖11中可以看到橫向阻尼為1.6和1.4時，張力中的突變現象明顯少于橫向阻尼為0.4和1.6時。即隨著橫向阻尼的逐漸增大，纜繩中張力的突變現象逐漸減少。圖12中的橫向阻尼與張力的最小二乘法擬合曲線整體呈勺狀，且纜繩在橫向阻尼為0.4～0.5之間張力達到最小。

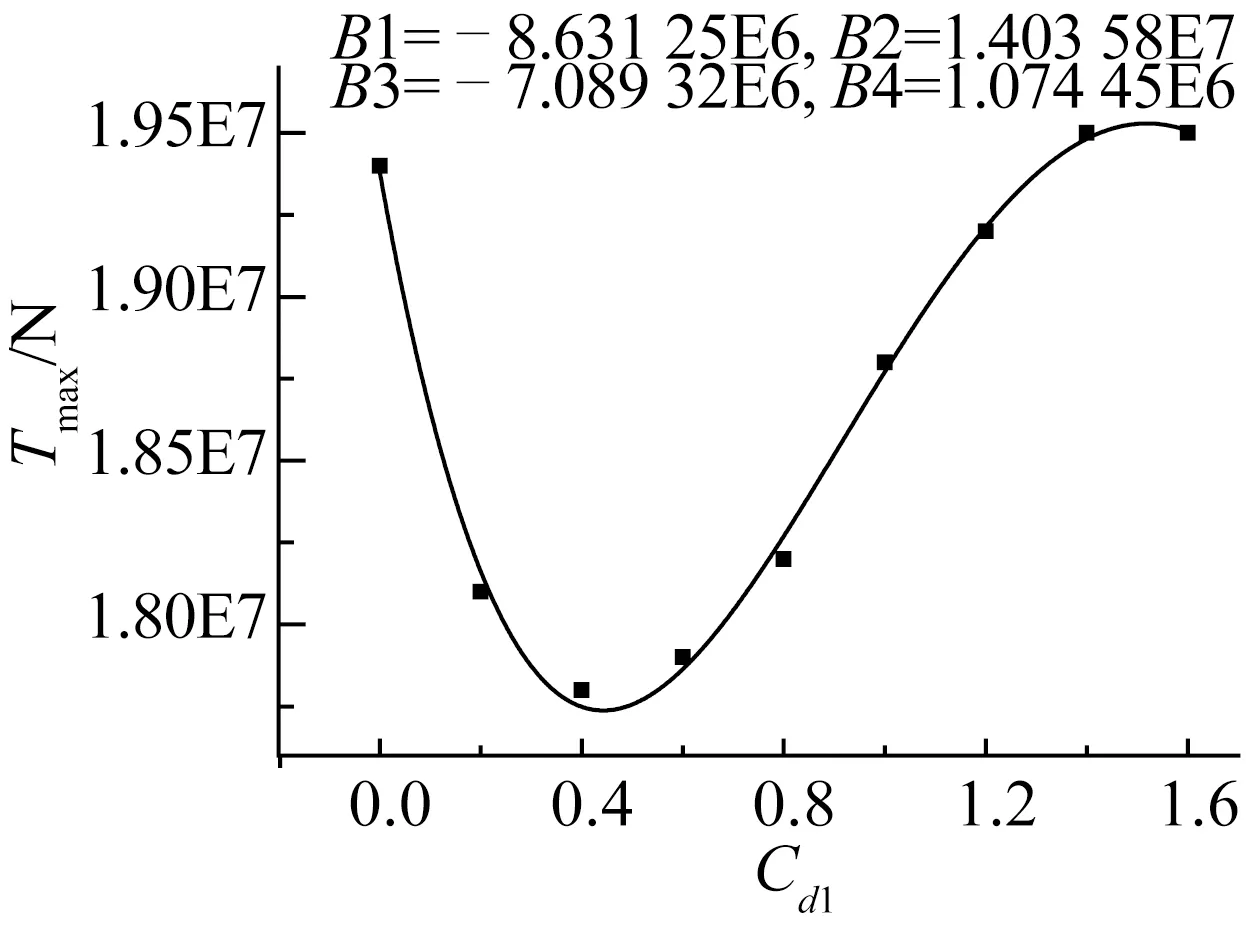
圖12 橫向阻尼與纜繩張力關系曲線Fig.12 The relation between transverse drag and cable tension

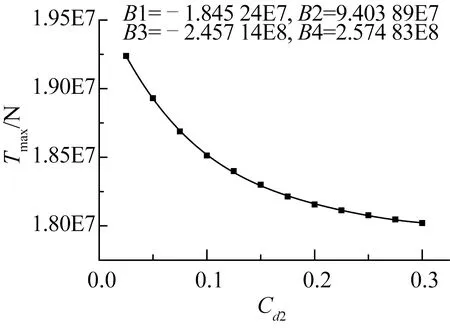
圖13 動態張力與縱向阻尼系數關系曲線Fig.13 The relation between inline drag and tension

設定橫向阻尼系數Cd1=1.25,計算不同縱向阻尼下纜繩的張力曲線，結果如圖14所示。從圖14中觀察到：縱向阻尼系數為0.05、 0.15時，張力曲線中突變現象出現較多；縱向阻尼系數為0.25、0.3時，張力曲線中的突變現象出現較少。隨著縱向阻尼系數的增大，與橫向阻尼一樣，張力中的突變現象也逐漸減少。圖13為縱向阻尼系數與纜繩張力的擬合曲線。與橫向阻尼不同，曲線整體呈下滑趨勢，隨著縱向阻尼系數的增加，纜繩中最大張力值逐漸下降。

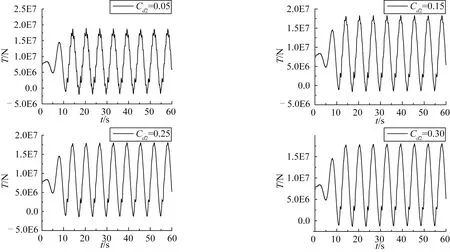
圖14 不同縱向阻尼時纜繩動態張力曲線Fig.14 The dynamic tension curve under different inline drag coefficent

3)激勵幅值對纜繩張力的影響

纜繩彈性模量E=1E11N/m2，激勵頻率f=1 rad/s，,取上端點激勵幅值A分別為3、4、5及6 m時，計算得到纜繩頂端的動態張力曲線如圖15所示。圖16為激勵幅值與纜繩張力的關系曲線，其中對幅值A小于4 m部分，采用線性擬合，斜率為1 992.27；對幅值大于4 m部分采用四階多項式進行擬合，擬合系數分別為B1=-288 878.58,B2=89 046.97，B3=-11 888.43,B4=585.60。

由圖15可以看到，在上端點激勵幅值為3 m和4 m時，纜繩頂端張力呈正弦規則變化，沒有出現突變現象。由此可知，此情況下不存在沖擊張力。這是由于激勵幅值為3 m、4 m時，上端點的運動不足以使纜繩恢復到松弛狀態，纜繩一直處于張緊狀態，不存在從松弛到張緊的轉變過程。當激勵幅值大于5 m時，纜繩存在從松弛到張緊的轉變過程，纜繩張力產生明顯的突變現象。由圖16可以看出，當激勵幅值小于4 m時，纜繩的動態張力隨激勵幅值呈線性增大；當激勵幅值大于5 m時，纜繩動態張力則隨激勵幅值呈非線性增大。

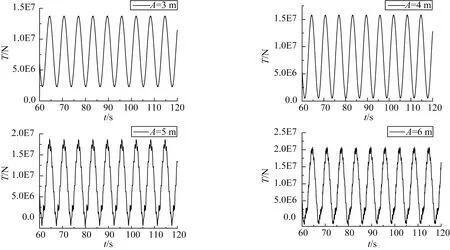
圖15 不同幅值激勵下纜繩張力曲線Fig.15 The tension curves of different amplitude under the excitation of the cable

圖16 激勵幅值與張力關系Fig.16 The relation curve between excitation amplitude and tension

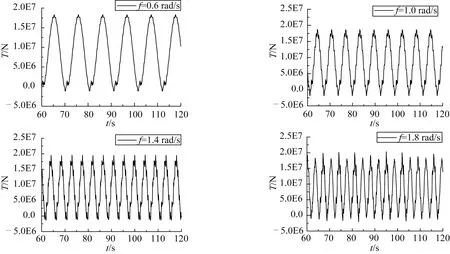
圖17 不同頻率下纜繩張力曲線Fig.17 The cable tension curve under different frequencies

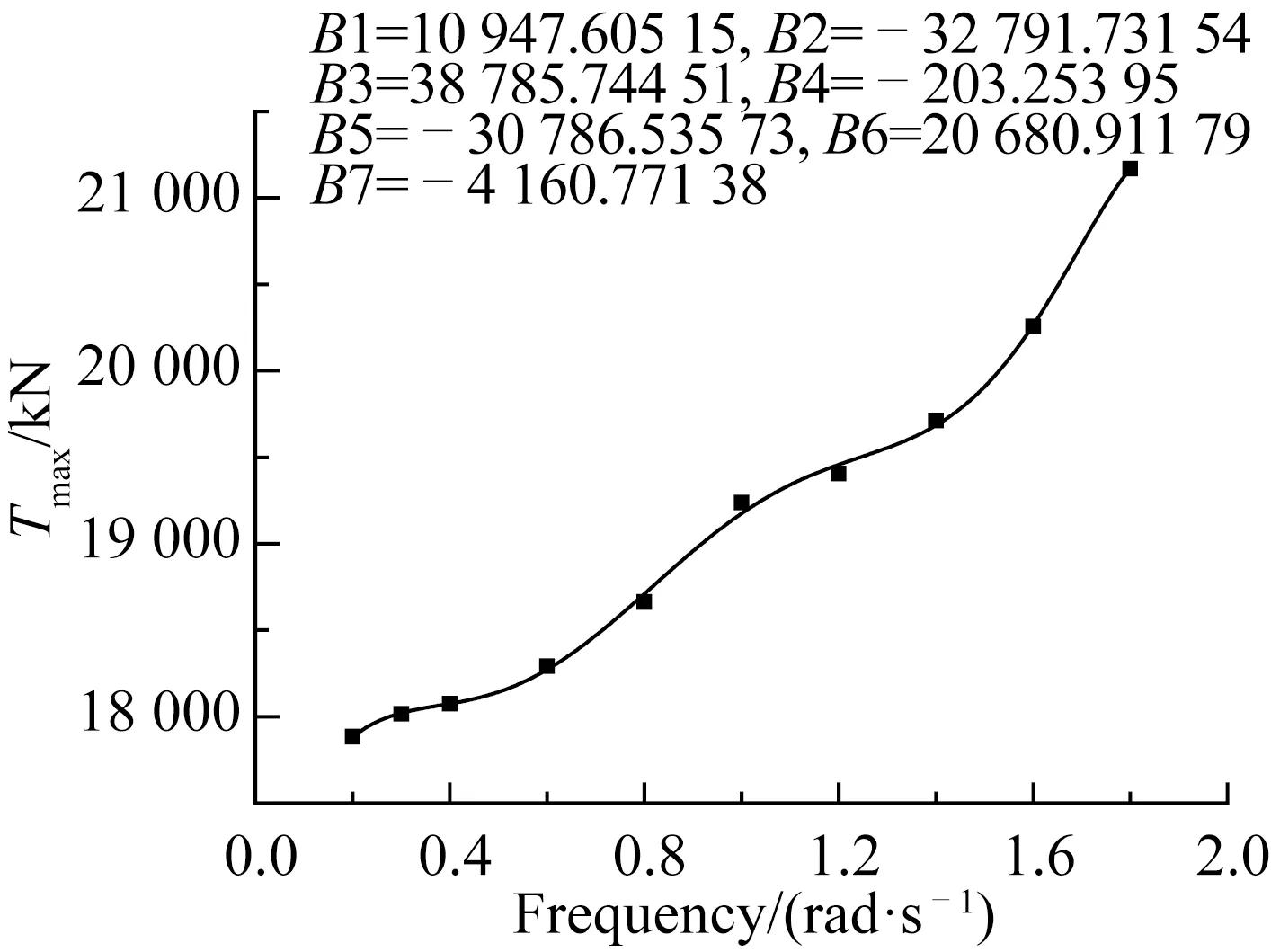
圖18 動態張力與激勵頻率關系Fig.18 The relation between tension and excitation frequencies

4)激勵頻率對纜繩張力的影響

纜繩彈性模量E=1E11N/m2，上端點激勵幅值A為5 m，取激勵頻率f分別為0.6、1.0、1.4和1.8 rad/s時，計算得到纜繩頂端的動態張力曲線如圖17所示。圖18為纜繩最大張力與激勵頻率關系圖。

從圖17可以看出：不同頻率下，纜繩從松弛到張緊轉變過程中均會產生沖擊張力；但是頻率較低時，張力曲線產生少量的突變現象，沖擊不明顯也不夠劇烈；頻率較大時，張力曲線產生大量的突變現象，沖擊比較明顯而劇烈。從圖18觀察得出：纜繩的動態張力隨激勵頻率的增加而呈非線性增加。

綜上所述，假設纜繩上端點為正弦激勵，纜繩的最大動態張力隨激勵幅值的增大而增大，隨頻率的增大而增大。這也印證了張素俠[8]的推斷：纜繩的最大動態張力可能與上端點的運動速度有關，運動速度越大，其最大動態張力也越大。

5) 彈性模量對纜繩張力影響

取上端點激勵幅值A為5 m，激勵頻率f為1 rad/s時，計算得到不同彈性模量下纜繩頂端的動態張力曲線，如圖19所示。

圖19 不同彈性模量纜繩動態張力Fig.19 The dynamic tension curves of different elastic modulus of the cable

可以看到，當彈性模量小于8E10 N/m2時，纜繩動態張力呈正弦變化，并未產生突變現象，其動態張力也未出現負值，此時不存在沖擊張力。當彈性模量大于8E10 N/m2時，纜繩的動態張力中出現比較明顯的突變現象。圖20為彈性模量與張力關系擬合曲線，E≤7E10 N/m2部分采用線性擬合，斜率為1.692 11E-4，纜繩中張力最大值隨彈性模量成線性增大；E≥8E10 N/m2部分采用4階多項式擬合，動態張力最大值與彈性模量則呈非線性上升趨勢。

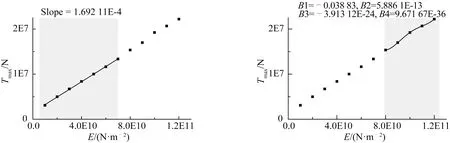
圖20 張力最大值與彈性模量關系Fig.20 The relation between the maximum tension and elastic modulus

3.3沖擊放大系數

沖擊放大系數表示系纜的最大動態張力與靜態張力的比值。以質量作為影響因素，研究不同質量系纜繩動態張力的沖擊放大系數。給定纜繩上端點激勵幅值為5 m，激勵頻率為1 rad/s，計算不同質量下纜繩的動態張力，計算結果如圖21所示。

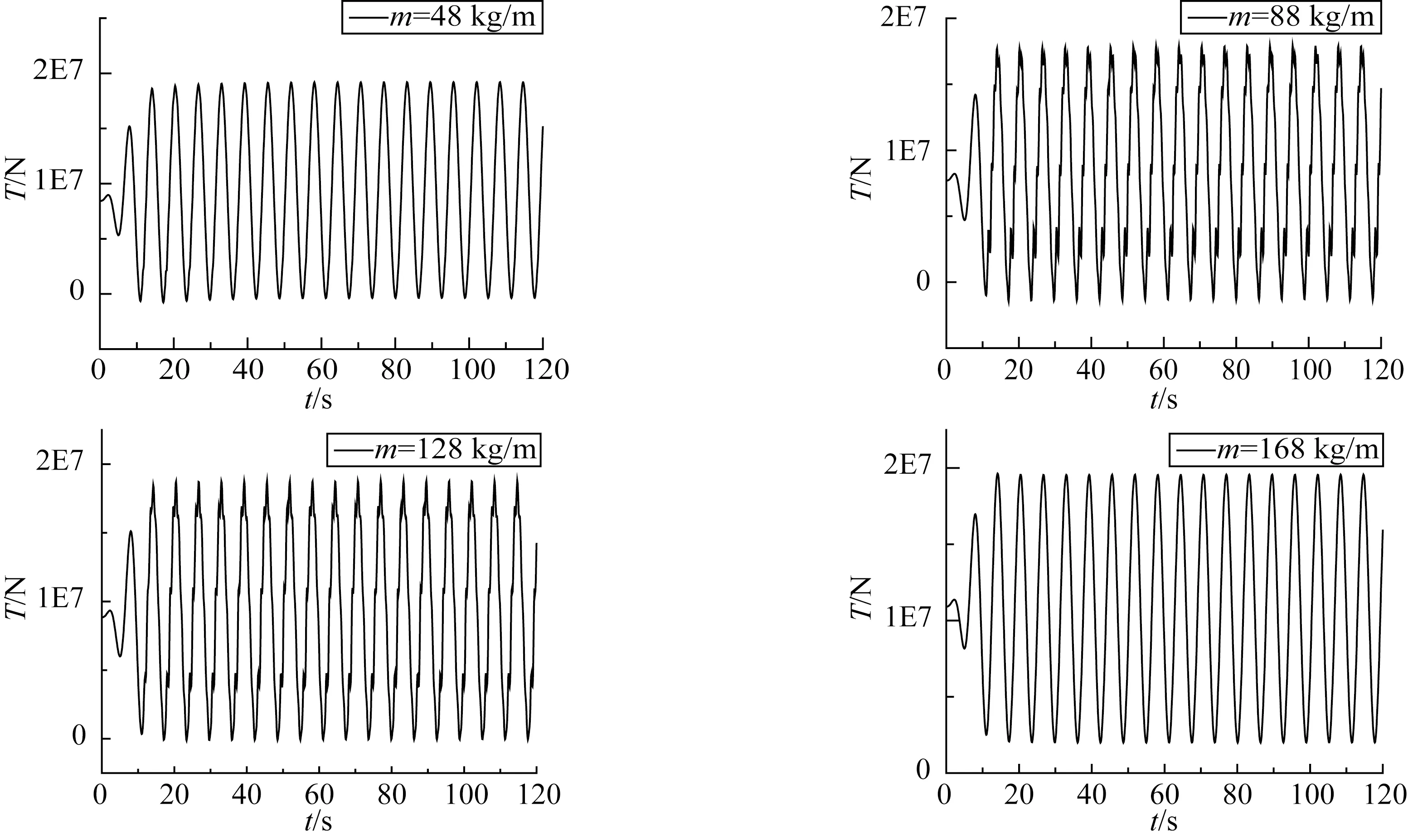
圖21 不同質量時纜繩的動態張力Fig.21 The dynamic tension cable of different qualities

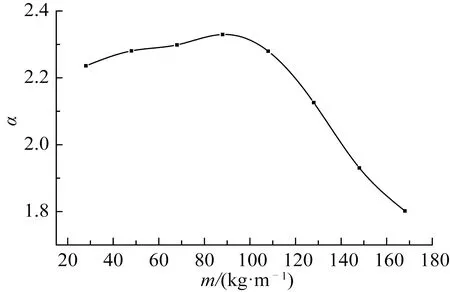
圖22 沖擊放大系數Fig.22 The impact of amplification factor

圖21研究了質量為48～168 kg/m時纜繩的動態張力，發現質量為68、88、108和128 kg/m時，動態張力中出現嚴重的沖擊載荷現象。 質量為28、48、148和168 kg/m時，動態張力則呈現平滑曲線，并無沖擊現象。這說明只有纜繩密度與海水密度相近時才會產生沖擊張力。進一步求得沖擊放大系數，結果如圖22所示。

由圖中看到，纜繩的沖擊放大系數在88 kg/m時最大，纜繩發生沖擊載荷時， 最大動態張力與靜態張力的比值要大于未發生沖擊載荷時的值。

4 結 語

通過對纜繩動態張力可能造成影響的幾種因素進行研究后發現，纜繩的動態張力最大值隨著初始預張力、彈性模量以及纜繩上端點激勵幅值和頻率的增大而增大；纜繩動態張力最大值在橫向拖曳力系數位于0.4～0.5之間達到最小，且隨著縱向拖曳力系數的增大而減小。這些影響因素不僅會影響纜繩動態張力的大小，也會對纜繩中的沖擊張力產生一定的影響。橫向阻尼越小，縱向阻尼越大，頻率越高，動態張力中突變發生越頻繁。需要特別指出的是，最后以單位質量為例對纜繩的沖擊張力展開研究，發現只有纜繩密度與海水密度相近時才會產生沖擊張力，且發生沖擊張力時的沖擊放大系數要大于未發生沖擊張力時的情況。

[1] PLAUT R H.Snapping-cable energy dissipater(SCED)for reducing seismic damage to structures[M].NSF Proposal,2001.

[2] PLAUT R H,ARCHILLA J C,MAYS T W.Snap loads in mooring lines during large three-dimensional motions of a cylinder[J].Nonlinear Dynamics,2000,23(3): 271-284.

[3] VASSALOS D,HUANG S,KOUROUKLIS A.Experimental investigation of snap loading of marine cables[C]//The Fourteenth International Offshore and Polar Engineering Conference.International Society of Offshore and Polar Engineers,2004.

[4] PASCOAL R,HUANG S,BARLTROP N.Assessment of the effect of mooring systems on the horizontal motions with an equivalent force to model[J].Ocean Engineering,2006,33(11): 1 644-1 668.

[5] 劉敏.海洋平臺系泊纜繩非線性動力學特性研究[D].鎮江: 江蘇科技大學,2015.(LIU Min.Study on nonlinear dynamic characteristics of mooring lines of offshore platform[D].Zhenjiang: Jiangsu University of Science and Technology,2015.(in Chinese))

[6] 趙晶瑞,范模,段夢蘭.深水系泊纜繩動力響應研究[J].船舶工程,2013(4):103-107.(ZHAO Jingrui,FAN Mo,DUAN Menglan.Study on dynamic response of deepwater mooring line[J].Ship engineering,2013 (4): 103-107.(in Chinese))

[7] 唐友剛,張素俠,張海燕,等.系泊系統松弛-張緊引起的沖擊張力研究[J].振動與沖擊,2008,27(4):70-72.(TANG Yougang,ZHANG Suxia,ZHANG Haiyan,et al.Study on the impact tension of mooring system relaxation tension strain [J].Vibration and shock,2008,27(4):70-72.(in Chinese))

[8] 張素俠.深海系泊系統松弛-張緊過程纜繩的沖擊張力研究[D].天津: 天津大學,2008.(ZHANG Suxia.Study on the impact of tension of mooring system in deep sea cable tension relaxation process[D].Tianjin: Tianjin University,2008.(in Chinese))

[9] 曹陽.深水系泊纜繩沖擊載荷實驗研究[D].天津: 天津大學,2009.(CAO Yang.Experimental study on load impact of deepwater mooring cable[D].Tianjin: Tianjin University,2009.(in Chinese))

[10] 張素俠,唐友剛,林維學,等.水下纜繩松弛-張緊過程的沖擊張力實驗研究[J].中國造船,2008,49(A02):385-390.(ZHANG Suxia,TANG Yougang,LIN Weixue,et al.Experimental study on the impact of underwater cable tension in taut slack process[J].Shipbuilding of China,2008,49 (A02): 385-390.(in Chinese))

Investigation on the impact tension characteristics of taut mooring lines

ZHANG Huoming1,XIE Zhuo1,FANG Guisheng2,KONG Lingbin1

(1.Zhejiang Provincial Key Laboratory of Flow Measurement Technology,China Jiliang University,Hangzhou 310018,China; 2.Mechanical and Automotive Engineering College,Zhejiang Water Conservancy and Hydropower College,Hangzhou 310018,China)

The impact force caused by the relaxation tension of the mooring line in the taut mooring system is studied by used of the method of lumped mass.Mooring lines discrete lumped mass model is established,the stress is analyzed and the equation of motion for the independent unit is established.Given cable endpoint harmonic excitation,through ANSYS/Aqwa,the response of cable movement is analyzed; the cable motion response process in three states is simulated and the impact tension conditions are discussed; and the initial cable tension,upper point excitation amplitude and frequency,drag effect of drag coefficient,elastic modulus and mass per unit length of dynamic tension are studied.The results show that these factors will not only affect the dynamic cable tension,but also have some influence on the impact load of cable.

taut mooring line; motion response; impact tension

P751

A

10.16483/j.issn.1005-9865.2017.05.003

1005-9865(2017)05-0023-10

2016-09-02

浙江省自然科學基金項目(Y14E090034,Y13F020140)；浙江省青年科學家培養計劃項目(2013R60G7160040)；上海交通大學海洋工程國家重點實驗室開放基金項目(1516)；衛星海洋環境動力學國家重點實驗室開放基金項目(SOED1706)

張火明(1976-)，男，湖北武穴人，博士后，副教授，主要研究領域為海洋工程流體力學。E-mail:zhm102018@163.com