適合移動云存儲的基于屬性的關鍵詞搜索加密方案

蘇 航 朱智強 孫 磊

(解放軍信息工程大學 鄭州 450000) (Suhang_039@163.com)

2017-06-12；

2017-07-27

國家重點研發計劃項目(2016YFB0501900) This work was supported by the National Key Research and Development Program of China (2016YFB0501900).

適合移動云存儲的基于屬性的關鍵詞搜索加密方案

蘇 航 朱智強 孫 磊

(解放軍信息工程大學 鄭州 450000) (Suhang_039@163.com)

近年來，隨著移動設備性能的不斷提升和移動互聯網的迅猛發展，越來越多的移動終端參與云端數據存儲與共享.為了更好地解決資源受限的移動設備參與云端數據共享的安全和效率問題，基于支持通配符的與門訪問結構，提出了一種高效的基于屬性的關鍵詞搜索加密方案，并證明了其在標準模型下滿足選擇關鍵詞明文攻擊的不可區分安全性和關鍵詞安全性.該方案采用韋達定理使得每個屬性僅需用一個元素表示，方案中索引長度固定，陷門和密鑰的長度及陷門算法和搜索算法的計算復雜度與訪問結構中可使用的通配符數量上限成正比，同時，移除了索引和陷門傳輸過程中的安全信道，進一步降低了開銷.效率分析表明：與其他方案相比，該方案的計算開銷和通信開銷較小，更加適用于移動云存儲環境.

移動云存儲；可搜索加密；屬性基加密；移除安全信道；韋達定理

便捷的移動終端已成為人們生活中不可或缺的一部分，移動用戶可通過移動游戲、移動支付等移動應用獲取多種服務.由于移動終端在存儲空間、通信帶寬及電池容量等多方面存在限制，移動應用提供的服務質量難以獲得顯著提升.為更好地支持日益復雜的移動應用并提升用戶體驗，云計算被引入到移動環境中[1].移動云計算作為一種將移動終端上復雜的數據存儲和處理操作置于云端的應用模式，可較好地解決移動終端資源受限的問題.

移動云存儲作為一種移動云計算的核心應用，具有容量可擴展、成本費用低、便于統一管理等諸多優勢，受到越來越多用戶的青睞.通過移動云存儲，用戶可高效便捷地在云端存儲和共享數據，包含個人隱私等信息的敏感數據往往也會存儲到云端，但數據上傳云端后，其實際物理控制權交由第三方云服務提供商.為防止云中存儲的敏感數據被云服務提供商或其他惡意用戶竊取，數據擁有者通常會在上傳敏感數據前對其進行加密處理.傳統的加密方式可保護數據的安全性，但是無法對數據實施靈活的訪問控制.Sahai和Waters[2]提出的屬性基加密(attribute-based encryption, ABE)方案可較好地同時解決數據安全性和數據訪問控制問題.在ABE方案中，密文和密鑰分別與一組屬性相關聯，加密者基于接收者的屬性特征制定相應的訪問策略，當且僅當解密者的屬性集合滿足訪問策略時可完成解密，ABE方案可有效實現一對多應用場景下細粒度的非交互訪問控制.

當數據以密文形式存儲在云端后，云服務提供商不能有效地為用戶提供數據檢索服務[3]，極大降低了云端數據的取用效率.Dan等人[4]提出了公鑰關鍵詞搜索加密(public key encryption with key-word search, PEKS)方案可實現密文數據檢索，但該方案僅支持一對一應用場景，不適用于云存儲環境.為了對云端數據實施細粒度的訪問控制并提供高效的密文檢索服務，Sun等人[5]、Zheng等人[6]、Qiu等人[7]結合ABE方案和PEKS方案，提出了多種基于屬性的關鍵詞搜索(attribute-based encryp-tion with keyword search, ABKS)方案.

現有的ABKS方案效率較低，對計算能力和通信帶寬有限的移動設備的影響尤為明顯，不能較好地適用于移動云存儲環境.主要表現在2個方面：1)在ABE方案中，隨著屬性數量增多，加解密算法計算復雜度和密文長度隨之線性增長，這就造成ABKS方案中索引和陷門算法計算復雜度以及索引和陷門長度隨屬性數量線性增長；2)在ABKS方案中，為保證方案的安全性，搜索服務器和用戶之間需要通過安全信道傳輸索引、陷門和搜索結果，而使用安全信道也將加重移動用戶端的計算和通信開銷.

針對ABE方案效率受屬性數量增加影響的問題，2007年Cheung等人[8]基于支持通配符的與門訪問結構，提出首個在標準模型下可證明安全的ABE方案，該方案具有較低的計算復雜度.Emura等人[9]、Zhang等人[10]和肖思煜等人[11]提出基于與門訪問結構的ABE方案，上述方案中的密文長度與解密算法中雙線性對運算量恒定，但不支持通配符，導致訪問策略的數量呈指數增長，且要求解密者屬性與訪問策略完全匹配，方案靈活性較差.Nishide等人[12]和Lai等人[13]的方案支持通配符，但方案中單個屬性需要用若干個元素表示，效率較低.Phuong等人[14]的方案支持通配符，該方案采用韋達定理使得各屬性只需用單個元素表示，此外方案還具有密文定長，解密算法中雙線性對運算量固定的優勢.Phuong等人[14]方案是選擇安全的，為提高方案安全性，Jin等人[15]對文獻[14]中的方案進行改進，基于合數群提出一種完全安全的ABE方案.

Baek等人[16]首次指出安全信道問題，他們指出在PEKS方案中，陷門和搜索結果易遭受惡意攻擊，為保證其安全，需要在搜索服務器和用戶之間建立安全信道.為移除安全信道，他們提出一種指定測試者的PEKS方案(PEKS with a designated tester, dPEKS)，通過使用指定搜索服務器的公鑰加密陷門和索引從而移除了安全信道.Rhee等人[17]考慮到來自惡意服務器和惡意接收者的攻擊，增強了Baek等人[16]方案的安全模型，并提出一種在隨機預言機模型下可證明安全的dPEKS方案.Fang等人[18]給出選擇密文攻擊安全、選擇關鍵詞攻擊安全并且可抵抗關鍵詞攻擊的安全模型，基于上述模型提出在標準模型下可證明安全的dPEKS方案.林鵬等人[19]提出一種通過指定搜索服務器從而移除安全信道的ABKS方案.

本文構造了一種適用于移動云環境的ABKS方案，其主要優勢體現在4個方面：

1) 方案采用支持通配符的與門訪問結構，受到Phuong等人[14]方案的啟發，使用不同屬性出現的“位置”匹配訪問策略與用戶屬性，并基于韋達定理實現解密過程中通配符的移除.傳統方案為支持通配符需要用多個元素表示一個屬性，而本方案一個屬性只需要用一個元素表示，效率更高.

2) 無需建立用戶列表.在Sun[5]與Qiu[7]的方案中，數據擁有者需要建立一個合法數據使用者列表，當系統中加入新用戶時數據擁有者需要更新該列表，即要求數據擁有實時在線.本文采用不同的索引生成方式，無需建立用戶列表.

3) 移除安全信道.授權機構為用戶選擇相對可信的搜索服務器，搜索過程中使用該搜索服務器的公鑰加密索引或陷門，即使惡意用戶截獲索引或陷門也無法從中獲取關鍵詞信息，移除了索引和陷門傳輸過程中的所需的安全信道，減輕了用戶的通信開銷.

4) 計算與通信開銷低.方案中索引和陷門算法的計算復雜度較小,索引長度固定，陷門長度較短，降低了用戶在搜索過程中的計算開銷和通信開銷.

1 預備知識

1.1雙線性映射及復雜性假設

定義1. 非對稱雙線性映射.令G1,G2,GT表示階為素數p的乘法循環群，若e:G1×G2→GT為有效的雙線性映射，則其滿足性質：

1) 雙線性.?g∈G1,h∈G2，a,b∈p，e(ga,hb)=e(gb,ha)=e(g,h)a b.

2) 非退化性.?g∈G1,h∈G2，e(g,h)≠1.

3) 可計算性.?g∈G1,h∈G2，存在多項式時間算法計算e(g,h).

若G1≠G2，該映射為非對稱雙線性映射.

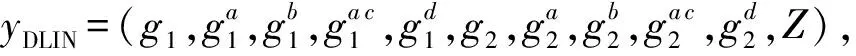
定義3. DDDH(divisible decision Diffie-Hellman)假設.令G表示階為素數p的乘法循環群，g為群G的生成元，給定元組yDDDH=(g,ga,gb,Z)，其中a,b∈p，Z∈G.在多項式時間內判定是否成立是困難的.

1.2訪問結構

定義4. 支持通配符的與門訪問結構.系統屬性集合為U={Att1,Att2,…,AttL}，其中屬性Atti的屬性值為Ai.系統中用戶的屬性集合為S={S1,S2,…,SL}，Si的取值有2種，即“+”和“-”.訪問結構為W={W1,W2,…,WL}，Wi的取值有“+”,“-”和“*”3種，其中“*”表示通配符，當屬性取值為“*”時表示訪問結構對此屬性不做要求.S|=W表示屬性集合S滿足訪問結構W.

1.3韋達定理[15]

向量A=(v1,v2,…,vL)，B=(z1,z2,…,zL)，A中包含字符和通配符，B中僅包含字符.向量A中通配符的數量為n，集合J={j1,j2,…,jn}表示通配符在A中出現的位置.

命題?i∈[1,L],v1=zi∨vi=*,可表述為

).

(1)

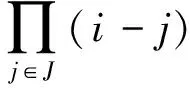
(2)

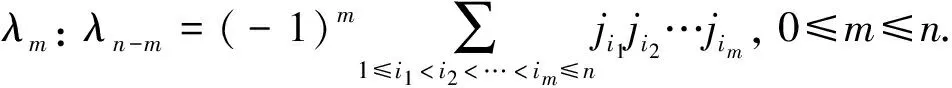
將式(2)代入式(1)中可得:

(3)

引入隨機群元素Hi隱藏式(3)中的運算，可得:

(4)

2 算法定義及安全模型

2.1系統模型

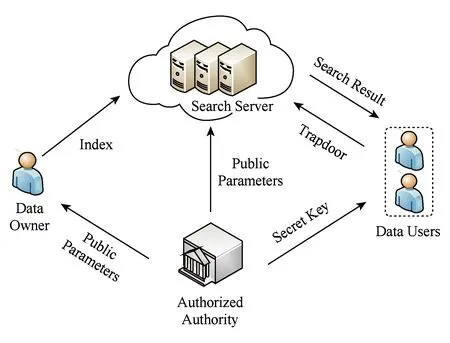
Fig. 1 System model圖1 系統模型

系統中包含4類實體，即授權機構(authorized authority, AA)、搜索服務器(search server, SS)、數據擁有者(data owner, DO)和數據使用者(data user, DU)，系統結構如圖1所示:

1) 授權機構

授權機構是系統中唯一的可信第三方，負責系統建立和密鑰生成工作.

2) 搜索服務器

搜索服務器是“誠實但具有好奇心的”，為用戶提供關鍵詞搜索服務.

3) 數據擁有者

從授權機構處獲取公開參數后，數據擁有者為敏感數據選取關鍵詞，對該關鍵詞加密生成索引并上傳至云端.

4) 數據使用者

從授權機構獲取密鑰后，通過生成搜索陷門，數據使用者可從搜索服務器處獲取關鍵詞搜索服務.

2.2算法定義

定義5. 本文提出的方案包括6個算法，定義為

Setup(1λ)→(PP,MSK)系統建立算法由授權機構運行.算法輸入為安全參數，輸出為系統公開參數PP以及系統主密鑰MSK.

SSKeyGen(PP)→(SKS,PKS)搜索服務器密鑰生成算法由授權機構運行.算法輸入為系統公開參數PP，輸出為搜索服務器公私鑰對(SKS,PKS).

KeyGen(PP,MSK,S)→SK密鑰生成算法由授權機構運行.算法輸入為系統公開參數PP、系統主密鑰MSK以及用戶屬性集S，輸出為用戶密鑰SK.

EncIndex(PP,KW,W,PKS)→IX索引算法由數據所有者運行.算法輸入為系統公開參數PP、數據擁有者為數據選取的關鍵詞KW、為索引制定的訪問結構W以及搜索服務器公鑰PKS，算法輸出為索引IX.

GenTrapdoor(PP,SK,SKW)→TR陷門算法由數據使用者運行.算法輸入為系統公開參數PP、數據使用者的密鑰SK和待搜索關鍵詞SKW，算法輸出為陷門TR.

Search(IX,TR,SKS)→SR搜索算法由搜索服務器運行.算法輸入為索引IX、陷門TR及搜索服務器私鑰SKS，算法輸出為搜索結果SR.

2.3安全模型

定義6. 選擇關鍵詞攻擊安全游戲[6].為保證索引不會泄漏數據擁有者為云端存儲數據選取的關鍵詞信息，方案需要達到選擇關鍵詞明文攻擊的不可區分性安全(IND-CKA).攻擊者和挑戰者之間在選擇模型下的攻擊游戲定義如下：

初始化：敵手選取待挑戰的訪問結構W*.

系統建立：挑戰者運行系統建立算法，將系統公開參數PP交給敵手.

階段1：敵手發起多項式次數的密鑰查詢.敵手向挑戰者提交待查詢的屬性集合S，若S不滿足W*，挑戰者運行密鑰生成算法，將該屬性集合對應的密鑰SK交給敵手；否則，挑戰者不響應此次查詢.

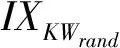
階段2：階段2與階段1相同，敵手不能查詢滿足訪問結構W*的屬性集合S對應的密鑰.

猜測：敵手輸出對rand的猜測rand′.

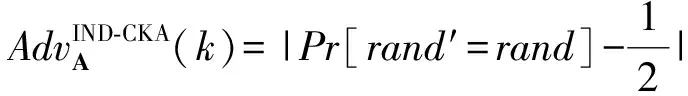
定義7. 關鍵詞安全性游戲[6].為保證數據使用者生成的陷門不會泄漏其搜索的關鍵詞信息，方案需要保證陷門中關鍵詞的安全性.攻擊者和挑戰者之間在選擇模型下的攻擊游戲定義如下：

系統建立：挑戰者運行系統建立算法，將系統公開參數PP交給敵手.

階段1：敵手發起多項式次數的密鑰和陷門查詢.

OKeyGen敵手向挑戰者提交待查詢的屬性集合S，挑戰者運行密鑰生成算法，將該屬性集合對應的密鑰SK交給敵手.

OTrapdoor敵手向挑戰者提交待查詢的屬性集合S和待查詢關鍵詞，挑戰者運行密鑰生成算法與陷門生成算法，將相應的陷門TR交給敵手.

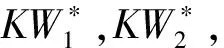
階段2：階段2與階段1相同，敵手不能查詢屬性集合S*對應的密鑰及陷門.

猜測：敵手輸出對rand的猜測rand′.

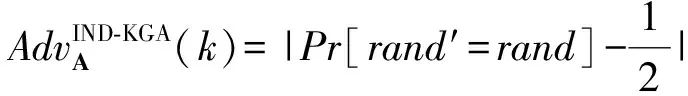
3 方案設計

3.1ABKS方案

本節提出一種高效的基于屬性的關鍵詞搜索加密方案，具體設計如下：

Setup(1λ)→(PP,MSK).

系統屬性集合為U，定義訪問結構中通配符的最大數量為N1，正屬性的最大數量為N2，負屬性的最大數量為N3.輸入安全參數后，授權機構按照下列步驟執行系統建立算法：

1) 選取階為素數p的乘法循環群G1,G2,GT，存在雙線性映射e:G1×G2→GT，生成元g1∈G1，g2∈G2.

2) 隨機選取α,β,γ∈p，計算

3) 對屬性集合中的所有屬性，隨機選取?i∈Uai∈p，計算Ai，1=，Ai,2=.

4) 選取密碼學散列函數：H:{0,1}*→p.

SSKeyGen(PP)→(SKS,PKS).

搜索服務器選取b∈p，其私鑰為公鑰PKS={PKS，1,PKS,2}，秘密保存私鑰，并公開其公鑰.

KeyGen(PP,MSK,S)→SK.

授權機構審核用戶提交的屬性集合S，若通過審核，授權機構按照下述步驟執行密鑰生成算法：

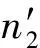
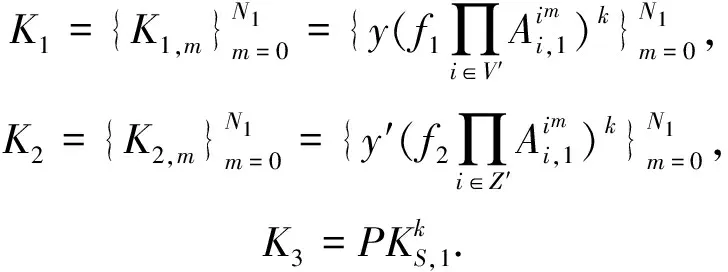
通過安全信道將密鑰SK={K1,K2,K3}發送給用戶.

EncIndex(PP,KW,W,PKS)→IX.

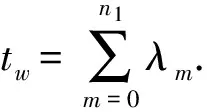
索引為

IX={J,IX1,IX2,IX3,IX4}.
GenTrapdoor(PP,SK,SKW)→TR.

數據使用者輸入密鑰SK和待搜索關鍵詞SKW.選取隨機數s∈p，計算搜索陷門為TR={T1,T2,T3}.

Search(IX,TR,SKS)→SR.

搜索服務器根據索引中通配符出現的位置J={w1,w2,…,wn1}，通過韋達定理計算1.3節式(2)中的λ={λ0,λ1,…,λn1}，計算:

R=e(IX3,T3)e(IX4,T3)，

測試L=R是否成立，若成立，SR=1,否則SR=0.

3.2正確性分析

分別計算等式左側和右側，可得：

R=e(IX3,T3)e(IX4,T3)=

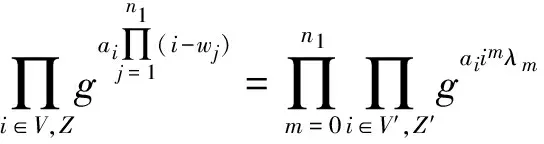
4 方案分析

4.1安全性證明

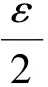
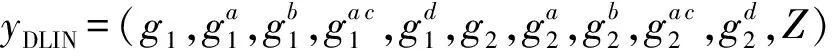
敵手A與仿真器B之間的游戲如下：

初始化：敵手A選取待挑戰的訪問結構W*，W*中包含n1個通配符、n2個正屬性和n3個負屬性，其中，通配符出現的位置為J={w1,w2,…,wn1}，正屬性出現的位置為V={v1,v2,…,vn2}，負屬性出現的位置為Z={z1,z2,…,zn3}.

根據通配符出現位置J={w1,w2,…,wn1}計算λ={λ0,λ1,…,λn1}.

系統建立：仿真器B運行系統建立算法，設置訪問結構中通配符數量最多為N1≥n1個.選取β,γ∈p，對系統中的屬性選取ai∈p，Ai，2=.令

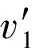
將密鑰SK={K1,K2,K3}發送給用戶；若S滿足W*，仿真器B不響應此次查詢.敵手A進行多項式次數的查詢.

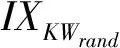
階段2：階段2與階段1相同，敵手A不能查詢滿足訪問結構W*的屬性集合S對應的密鑰.

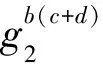
1) 若rand′≠rand，則：

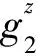
2) 若rand′=rand，敵手的優勢為ε，則：

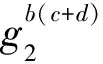
故挑戰者C在DLIN游戲中的優勢為

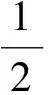
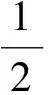
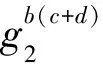
證畢.

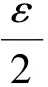
證明. 挑戰者C通過構造仿真器B來模擬不可區分游戲.挑戰者C將將群G1中的DDDH數組yDDDH=(g,ga,gb,Z)交給仿真器B.

敵手A與仿真器B之間的游戲如下：

系統建立：仿真器B運行系統建立算法.選取β,γ∈p，y=ga，令f1=gβ，f2=gγ，選取ai∈p，Ai=gai.選取b′∈p令搜索服務器公鑰為PKS=(gb)b′.將系統公開參數PP交給敵手A.

階段1：敵手A發起多項式次數的密鑰和陷門查詢.

OKeyGen：敵手A向仿真器B提交待查詢的屬性集合S，仿真器B按照正負屬性出現的位置，將S解

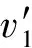
將密鑰SK={K1,K2,K3}發送給用戶.敵手A進行多項式次數的查詢.

OTrapdoor：敵手A向仿真器B提交待查詢的屬性集合S和關鍵詞SKW，仿真器B運行密鑰生成算法與陷門生成算法，選取隨機數s∈p，計算：

將相應的陷門TR交給敵手A.

挑戰：敵手A向仿真器B提交待挑戰的屬性集合S*及關鍵詞SKW1,SKW2，階段1中敵手A未查詢S*對應的密鑰及陷門.仿真器B選取隨機數rand∈{0,1}，運行密鑰生成算法與陷門生成算法.選取隨機數s′∈p，令s=，計算：

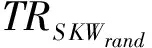
階段2：階段2與階段1相同，敵手A不能查詢屬性集合S*對應的密鑰及陷門.

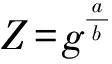
1) 若rand′≠rand，則：

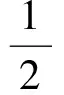
2) 若rand′=rand，敵手的優勢為ε，則：

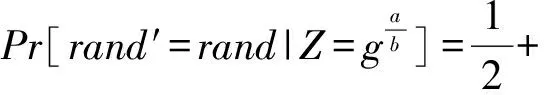
故挑戰者C在DDDH游戲中的優勢為

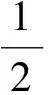
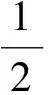
證畢.

4.2效率分析

方案效率對于資源受限的移動設備具有重要影響，表1從計算開銷和通信開銷2個方面將本文方案與近年來的經典方案[5,7,19]進行效率對比.

表1中E1,E2分別表示執行一次群G,GT上指數運算的時間，P表示執行一次雙線性對運算的時間，由于上述運算的計算復雜度遠遠高于算法中的其他運算，因此計算復雜度對比主要考慮上述運算；N表示系統中的屬性總數，ni表示多值與門結構中每個屬性的屬性值數量，M表示訪問結構中使用的通配符數量上限，其中M?N；|G|表示群G中元素的長度，|GT|表示群GT中元素的長度.

計算開銷對比如表1中的列2～4所示.由于索引算法、陷門算法由用戶在移動終端上執行，搜索算法需要搜索服務器與多個用戶進行交互，這3個算法的計算開銷對用戶體驗的影響最大，因此主要對比這3個算法的計算復雜度.如表1所示，本文方案中索引算法的計算復雜度與系統屬性線性相關，較文獻[7,19]中的方案具有一定的優勢，陷門算法和搜索算法與訪問結構中可使用的通配符數量上限成正比，由于訪問結構中可使用的通配符數量往往遠小于系統中的屬性數量，因此較其他方案本文方案中的陷門算法和搜索算法較其他方案具有較低的計算復雜度.

通信開銷對比如表1中的后4列所示.在搜索過程中，移動終端用戶與授權機構、搜索服務器之間需要傳輸密鑰、索引等參數，這些參數的長度將給帶寬受限的移動設備帶來一定的負擔，通信開銷主要對公開參數、密鑰、索引和陷門的長度進行對比.本文方案中索引長度定長，密鑰長度和陷門長度與訪問結構中可使用的通配符數量上限成正比，由于M?N，本文方案中密鑰長度和陷門長度較其他方案也具有較短的長度.此外，本文與文獻[19]移除了安全信道，進一步降低了通信開銷.

本文通過仿真實驗對算法進行評估，實驗的硬件環境為Intel Core i5，2.4 GHz處理器，操作系統為環境為64位Windows10操作系統，實驗基于Charm[20]架構，選用JPBC中的D類橢圓曲線.選取系統屬性總量N=50，令通配符總量M從1～10變化.實驗結果如圖2所示，索引算法隨通配符數量增加呈線性減少趨勢，而陷門和搜索算法隨之呈線性增長趨勢.

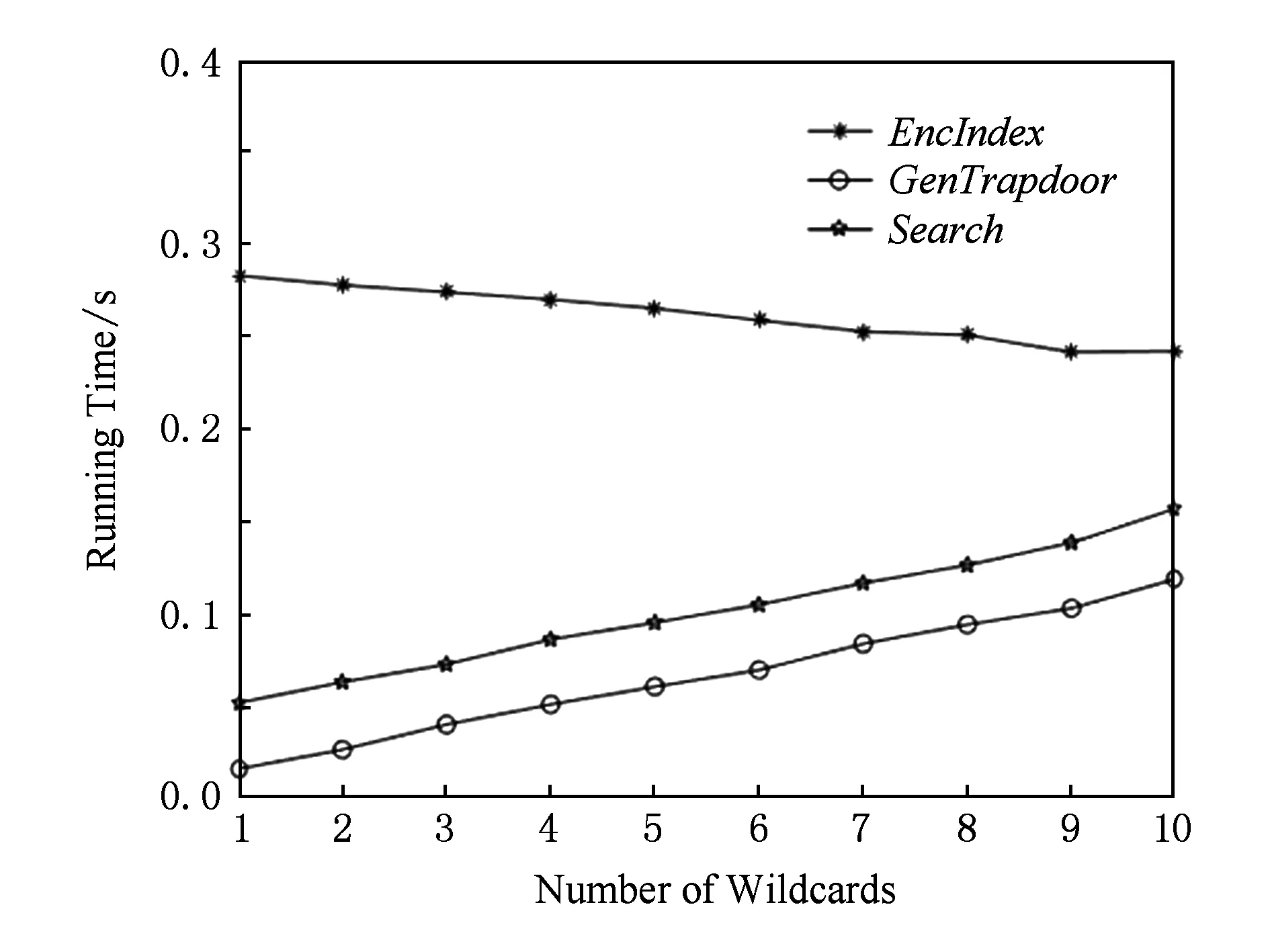
Fig. 2 The influence of wildcards number on running time圖2 通配符數量對方案運行時間的影響

5 總 結

針對現有ABKS方案計算開銷和通信開銷較大，不能較好地支持移動設備的問題，本文提出一個適用于移動云存儲環境的ABKS方案，該方案在標準模型下滿足IND-CKA安全性和關鍵詞安全性.與經典方案相比，本方案具有較低的計算開銷和通信開銷.本文的IND-CKA安全性證明是在選擇模型下進行的，在未來研究中將對方案的安全性進行進一步提升，構造標準模型下完全安全的新方案.

[1] Cui Yong, Song Jian, Miao Congcong, et al. Mobile cloud computing research progress and trends[J]. Chinese Journal of Computers, 2017, 40(2): 273-295 (in Chinese)

(崔勇, 宋健, 繆蔥蔥, 等. 移動云計算研究進展與趨勢[J]. 計算機學報, 2017, 40(2): 273-295)

[2] Sahai A, Waters B. Fuzzy identity-based encryption[G] //LNCS 3494: Proc of the 24th Int Conf on the Theory and Applications of Cryptographic Techniques. Berlin: Springer, 2005: 457-473

[3] Li Hui, Sun Wenhai, Li Fenghua, et al. Secure and privacy-preserving data storage service in public cloud[J]. Journal of Computer Research and Development, 2014, 51(7): 1397-1409 (in Chinese)

(李暉, 孫文海, 李鳳華, 等. 公共云存儲服務數據安全及隱私保護技術綜述[J]. 計算機研究與發展, 2014, 51(7): 1397-1409)

[4] Dan B, Crescenzo G D, Ostrovsky R, et al. Public key encryption with keyword search[G] //LNCS 3027: Proc of the 23rd Int Conf on the Theory and Applications of Cryptographic Techniques. Berlin: Springer, 2004: 506-522

[5] Sun Wenhai, Yu Shucheng, Lou Wenjing, et al. Protecting your right: Verifiable attribute-based keyword search with fine-grained owner-enforced search authorization in the cloud[J]. IEEE Trans on Parallel & Distributed Systems, 2016, 27(4): 1187-1198

[6] Zheng Qingji, Xu Shouhuai, Ateniese G. VABKS: Verifiable attribute-based keyword search over outsourced encrypted data[C] //Proc of the 33rd IEEE Int Conf on Computer Communications. Piscataway, NJ: IEEE, 2014: 522-530

[7] Qiu Shuo, Liu Jiqiang, Shi Yanfeng, et al. Hidden policy ciphertext-policy attribute-based encryption with keyword search against keyword guessing attack[J]. Science China Information Sciences, 2017, 60(5): 052105

[8] Cheung L, Newport C. Provably secure ciphertext policy ABE[C] //Proc of the 14th ACM Conf on Computer and Communications Security. New York: ACM, 2007: 456-465

[9] Emura K, Miyaji A, Omote K, et al. A ciphertext-policy attribute-based encryption scheme with constant ciphertext length[J]. International Journal of Applied Cryptography, 2010, 2(1): 46-59

[10] Zhang Yinghui, Dong Zheng, Chen Xiaofeng, et al. Computationally efficient ciphertext-policy attribute-based encryption with constant-size ciphertexts [G]//LNCS 8782: Proc of the 8th Int Conf on Provable Security. Berlin: Springer, 2014: 259-273

[11] Xiao Siyu, Ge Aijun, Ma Chuangui. Decentralized attribute-based encryption scheme with constant-size ciphertexts[J]. Journal of Computer Research and Development, 2016, 53(10): 2207-2215 (in Chinese)

(肖思煜, 葛愛軍, 馬傳貴. 去中心化且固定密文長度的基于屬性加密方案[J]. 計算機研究與發展, 2016, 53(10): 2207-2215)

[12] Nishide T, Yoneyama K, Ohta K. Attribute-based encryption with partially hidden encryptor-specified access structures [G]//Proc of the 5th Int Conf on Applied Cryptography and Network Security. Berlin: Springer, 2008: 111-129

[13] Lai Junzuo, Deng R H, Li Yingjun. Fully secure cipertext-policy hiding CP-ABE [G]//LNCS 6672: Proc of the 7th Int Conf on Information Security Practice and Experience. Berlin: Springer, 2011: 24-39

[14] Phuong T V X, Yang Guomin, Susilo W. Hidden ciphertext policy attribute-based encryption under standard assumptions[J]. IEEE Trans on Information Forensics & Security, 2015, 11(1): 35-45

[15] Jin Cancan, Feng Xinyu, Shen Qingni. Fully secure hidden ciphertext policy attribute-based encryption with short ciphertext size[C] //Proc of the 16th Int Conf on Communication and Network Security. New York: ACM, 2016: 91-98

[16] Baek J, Safavinaini R, Susilo W. Public key encryption with keyword search revisited [G] //LNCS 5072: Proc of the 6th Int Conf on Computational Science and Its Applications. Berlin: Springer, 2008: 1249-1259

[17] Rhee H S, Susilo W, Kim H. Secure searchable public key encryption scheme against keyword guessing attacks[J]. IEICE Electronics Express, 2009, 6(5): 237-243

[18] Fang Liming, Susilo W, Ge Chunpeng, et al. Public key encryption with keyword search secure against keyword guessing attacks without random oracle[J]. Information Sciences, 2013, 238(7): 221-241

[19] Lin Peng, Jiang Jie, Chen Tieming. Application of keyword searchable encryption in cloud[J]. Journal on Communications, 2015, 36(S1): 259-265 (in Chinese)

(林鵬, 江頡, 陳鐵明. 云環境下關鍵詞搜索加密算法研究[J]. 通信學報, 2015, 36(S1): 259-265)

[20] Akinyele J A, Garman C, Miers I, et al. Charm: A framework for rapidly prototyping cryptosystems[J]. Journal of Cryptographic Engineering, 2013, 3(2): 111-128

Attribute-BasedEncryptionwithKeywordSearchinMobileCloudStorage

Su Hang, Zhu Zhiqiang, and Sun Lei

(PLAInformationEngineeringUniversity,Zhengzhou450000)

In recent years, with the further improvement of mobile devices’ performance and the rapid development of mobile Internet, more and more mobile terminals participate in cloud data storage and data sharing. In order to support mobile devices with constrained resource effectively in terms of sharing data safely and efficiently in the cloud, a secure and efficient attribute-based encryption scheme with keyword search (ABKS) is proposed in this paper. The proposed scheme is based on the AND gate access structure with wildcards, which is proven to be IND-CKA (indistinguishable against chosen keyword attack) secure and achieves keyword security under the standard model. The scheme adopts the Viète’s formulas to make each attribute only be represented by one element, and the length of index is constant, the length of trapdoor and secret key and the computation complexity of trapdoor algorithm and search algorithm grow linearly with the maximum number of wildcards that can be used in the access structure, in addition, the scheme removes the secure channel, which reduces the communication overhead further during the transmission process of index and trapdoor. Efficiency analysis shows that compared with other schemes, the proposed scheme has less computation overhead and communication overhead, which is more suitable for mobile cloud storage environment.

mobile cloud storage; searchable encryption; attribute-based encryption (ABE); secure-channel free; Viète’s formulas

TP390

SuHang, born in 1994. Master candidate. Her main research interests include public key encryption.

ZhuZhiqiang, born in 1961. PhD, professor. His main research interests include cloud computing and information security (zhiqiang_zhu_zz@163.com).

SunLei, born in 1973. PhD, professor. His main research interests include cloud computing and information security (sl0221@sina.com).