基于塊相關框架的多參考微擾理論和多參考耦合簇理論

鄒競祥 沈 軍 許恩華 方 濤 黎書華,*

(1南京大學化學化工學院，介觀化學教育部重點實驗室，理論與計算化學研究所，南京 210023；2Department of Chemistry,Michigan State University, East Lansing, Michigan 48824, United States；3Graduate School of System Informatics,Kobe University, Kobe, Hyogo 657-0025, Japan)

基于塊相關框架的多參考微擾理論和多參考耦合簇理論

鄒競祥1沈 軍2許恩華3方 濤1黎書華1,*

(1南京大學化學化工學院，介觀化學教育部重點實驗室，理論與計算化學研究所，南京 210023；2Department of Chemistry,Michigan State University, East Lansing, Michigan 48824, United States；3Graduate School of System Informatics,Kobe University, Kobe, Hyogo 657-0025, Japan)

傳統單參考電子相關方法已經發展成熟，但很多時候無法正確描述共價鍵解離、雙(多)自由基和激發態等電子之間相關性非常強的體系。近年來發展的多參考微擾理論和多參考耦合簇理論以多個行列式的線性組合為參考波函數，采用不同的方式有效考慮電子之間的動態相關，對強關聯體系的描述取得了顯著的改進。但根據理論出發點和精度要求的不同發展出了許多多參考理論，仍無一個公認的、令人滿意的方案。本文將結合與常見電子相關方法在理論框架和計算精度上的比較，詳細闡述塊相關理論的基本原理，并介紹基于塊相關的“另類”多參考電子相關方法。最后本文還簡單展望了多參考電子相關方法今后的發展趨勢。

多參考；塊相關微擾理論；塊相關耦合簇理論；多鍵解離；勢能面

1 引 言

單參考(single reference，SR)電子相關方法是一類基于Hartree-Fock(HF)理論的post-HF方法，自上個世紀30年代后一直以迅猛的態勢發展，并在過去幾十年內日臻成熟，成為主流的從頭算電子結構方法，廣泛應用于分子的電子結構計算。這里所謂的單參考，即選取一個HF行列式為參考態波函數，再以不同的方式將電子從占據軌道激發至空軌道上或直接引入更多的激發組態，來考慮電子之間的動態相關。前者處理動態相關常見的方法為多體微擾理論(many-body perturbation theory or M?ller–Plesset perturbation theory，MBPT或 MPn)和耦合簇理論(coupled cluster theory，CC)，后者則對應組態相互作用(configuration interaction，CI)方法。現在人們已經熟知，高效考慮動態相關的多體微擾理論和耦合簇理論可以在相同的計算標度下取得比組態相互作用方法更準確的計算結果，且計算結果具有大小一致性(截斷的 CI方法不具備)，可用于均衡處理不同大小的體系。尤其是單參考 CC方法，在描述許多問題時已經能達到化學精度(4?10 kJ·mol?1)1。然而大量的計算表明，傳統單參考方法只能精確描述勢能面上位于平衡結構附近的情況。許多重要的化學問題如共價鍵的解離、分子結構的拉伸和畸變、有機分子中的雙自由基或多自由基和光化學過程等等問題中，存在HOMO能級與LUMO能級簡并或準簡并的情況，這時電子之間的相關性非常強，一些組態與所選的單參考態可能占有同樣的比重，體系具有內秉的多參考態特征。對這些問題，單參考方法無法準確描述其勢能面，多體微擾方法的高階微擾項絕對值很大，結果不合理。基于HF的CCSD和CCSD(T)方法通常也無法給出定性正確的結論1?3。針對這種情形，一種通常的方法是停留在單參考態框架內使用非限制性的 HF行列式(UHF)作為參考態波函數4?8。這種方法有時在能量上得到定性正確的結果，但是UHF帶來的嚴重自旋污染(spin contamination)9?11問題，使得在此基礎上考慮動態相關的多體微擾理論和耦合簇理論得到的結果同樣有自旋污染，分子的各種性質難以得到描述。另一種途徑便是超越單參考框架，發展以多個HF行列式為參考態的電子相關方法，并試圖準確描述分子的各種性質。

如前所述，多參考(multireference，MR)電子相關方法即以多個行列式的線性組合為參考態波函數。若在此基礎上分別采用微擾項或激發算符的指數形式考慮電子之間的動態相關，則分別對應于多參考微擾理論(MRPT)和多參考耦合簇理論(MRCC)。與單參考方法截然不同的是，多參考方法在無論在理論的公式推導上、編程的實現難度上，還是軟件的使用方面，都比單參考方法復雜得多，且根據理論方法出發點和面對實際問題的不同衍生出許多變種方法，至今仍無一個公認的令人滿意的多參考理論方案。最簡單的多參考態波函數，可選取合適的活性軌道空間和活性電子數來構造，這就是完全活性空間自洽場(complete active space self-consistent field，CASSCF)波函數。Roos等人12發展的CASPT2方法便是基于CASSCF波函數的二階微擾方法，能獲得一定程度的動態相關。與單參考微擾方法類似，多參考微擾方法一般將零階哈密頓算符定義成使零階波函數為其本征函數，接著便可以使用微擾理論公式計算各階波函數和校正能量。Mukherjee等人近年來發展的特定態多參考微擾理論(state-specific MRPT，SS-MRPT)13,14具有大小一致性(size-consistency)和無侵入態(intruder state)問題，在眾多MRPT方法中比較有影響力。

相比單參考耦合簇理論，多參考耦合簇理論可以得到精度顯著改善的結果。近年來發展的多參考耦合簇理論可以大致分為以下三類：(1)Hilbert空間或普遍態(state-universal，SU)多參考耦合簇理論15?19，每次處理的電子態中電子數目不變；(2) Fock空間或普遍價(valence-universal，VU)多參考耦合簇理論20?25，可以處理不同電子數目的電子態；(3) 特定態(state-specific)或選擇態(state-selective，SS)多參考耦合簇理論26?30，每次處理一個特定的電子態。與SS-MRPT在微擾方法中的優勢一樣，SS-MRCC方法具有大小一致性和無侵入態問題，已經可以正確描述許多分子的解離勢能面31，但其精度還沒有達到公認的程度和較為理想的標準。另外，最直接的MRCC理論應當是以 CASSCF為參考波函數的 CAS-CCSD方法，考慮活性空間內所有組態函數對應行列式的單、雙重外部激發。該方法以Ivanov和Adamowicz等人的出色工作32,33為代表，已經被證明對解離勢能面有著高精度的描述，但其計算量驚人，經常用于理論上標定(benchmark)其他多參考方法，實際應用價值較小。另一方面，近年來還發展了一些“另類”多參考耦合簇策略(alternative MRCC methods)，試圖用類似SRCC理論的框架提供新的解決方案。Li和Paldus發展的約化多參考耦合簇(reduced MRCC，RMR-CC)方法34?37利用 CC-CI方法的轉化關系，從MRCI計算中引入近似的三、四重激發振幅并保持固定，而單、雙重激發算符的振幅仍由CCSD提供，在迭代計算中是可變量。RMR-CCSD方法已經在不少具有多參考特征的體系上取得了較好的結果34,38。不同于上述所有基于軌道相關(orbital-based)的MRCC方法，我們課題組提出了一種基于塊相關的多參考耦合簇理論(block-correlated coupled cluster theory ，BCCC)39?45。在該理論中我們將若干個軌道視為一個多軌道塊(multi-orbital block)，即軌道集合的子集；單個軌道看成一個特殊的單軌道塊(single-orbital block)。體系的波函數可以表示成各個塊最重要的多電子態的張量積，再利用耦合簇激發算符將電子在塊內進行激發或直接激發至別的塊上，從而囊括塊內的非動態相關能和塊與塊之間的動態相關能。若以CASSCF波函數為參考態，并將耦合簇算符截斷至四塊相關，對應的BCCC方法簡稱為 CAS-BCCC440,41。該方法計算量只比 CCSD略大，但精度優于 CASPT2和MR-CISD。

值得注意的是，無論是基于軌道相關的MRPT、MRCC還是基于塊相關的CAS-BCCC4，多以CASSCF波函數為參考態，當活性空間增大時組態數目眾多，計算量非常大，因此只能應用于較小的活性空間，這是這幾類方法的一大限制。不過，塊電子態和塊相關的概念允許我們走出這一限制，將其推廣至其他參考波函數上，比如廣義價鍵(generalized valence bond，GVB)波函數46即是一種“類多參考”(MR-like)的波函數，可以作為參考態使用。結合完美配對的 GVB波函數(GVB-PP)46，我們課題組先后發展了 GVB-BCPT2方 法44和 CASCI-BCPT2/GVB 方 法45及DMRG-BCPT2/GVB方法45，將每個軌道對(geminal)視為一個塊并以二階微擾的形式考慮塊與塊之間的動態相關，大大增加了可處理的活性空間。本文將結合與多參考領域內其他方法的區別和聯系，介紹我們課題組發展的基于塊相關理論框架的MRPT和MRCC理論，并列舉常見多參考研究體系的計算結果闡明目前方法的優勢和不足，最后對多參考方法未來的發展方向做一些討論。

2 塊相關多參考方法

傳統的單參考方法多以 HF行列式為參考波函數，在自旋軌道表示下，其二次量子化形式為

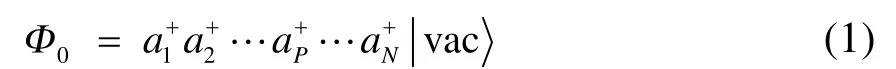
此時 Ai+I為塊產生算符。顯然，若包含多個自旋軌道，則其必定可以展開為多個行列式的線性組合；對應地，塊產生算符 Ai+I應是該塊內各自旋軌道產生算符乘積的線性組合。如果把每個塊內最重要的電子態記為，則(1)式可以用塊電子態的形式寫為

其中M為塊數。對一個占據單軌道塊，其最重要的電子態(基態)即為其占據態，激發組態即為真空態(電子被激發至別的塊內)；對于未占據單軌道塊則情況恰好相反。而對于多軌道塊，比如一含 4個自旋軌道的塊，若允許其電子數在 0?4之間變化，總共可以有24= 16個電子態(包括真空態，詳細表達式可以在Ref.40和Ref.44中找到)。另外，通過將多個塊中任意一個塊的電子態替換為它的某一個較高能量的電子態便可得單激發組態，形式如下：

式中 A1I為第I塊的最重要電子態對應的塊湮滅算符，多激發組態可以此類推。所以形如式(3)和(4)的波函數不僅可以表示單個HF行列式，還自然地包含了更為廣義的內涵：通過選取合適的塊，所有塊產生算符作用在真空態上會產生多個行列式線性組合的效果。這為我們采用其他形式的參考波函數提供了便利條件，如以CASSCF為參考態，可以將整個活性空間視為一個塊，其他自旋軌道均看作單軌道塊；若以GVB波函數為參考態，則可以自然地將每個軌道對看作一個多軌道塊，此時每個軌道塊只包含 4個自旋軌道，電子數可以在0?4之間變化。

塊相關耦合簇理論指的是將單參考理論框架中的單個自旋軌道的概念推廣為一個多軌道塊，并使用簇激發算符來處理塊與塊之間的動態相關。BCCC的波函數和指數算符表達式表觀上和SRCC一樣，

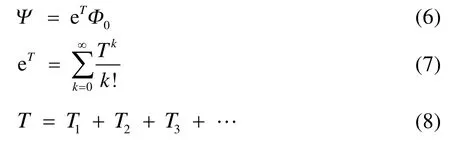
不同的是，有了塊的概念之后簇激發算符就變為產生塊內和塊間電子的激發：

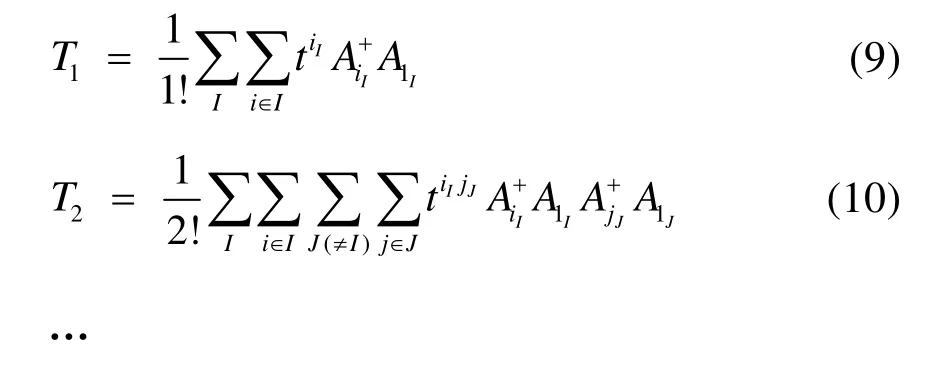
當簇激發算符截斷至 n塊時，對應的方法簡記為BCCCn。從上述分析和式(6)?(10)可以看出，BCCC實際上是一種“另類”多參考耦合簇方法。塊相關的概念不僅對 MRCC適用，對 MRCI和MRPT方法同樣適用。另一方面，如同SRCC能夠高效考慮動態相關的優點，BCCC理論上也是一種能夠高效獲得動態相關能的多參考方法。實際上早在BCCC理論第一次提出時，就已經被運用于一維或準一維的反鐵磁性 Heisenberg模型基態能量的計算39，計算表明BCCC2能夠得到準確基態能量值的 98.8%，BCCC3則可以得到比重99.5%以上的準確基態能量或 DMRG基態能量值(一維情況下DMRG結果極其接近準確值)。

2.1 CAS-BCCC4方法

前面已經提到，在 CAS-BCCC4中可以將參考態的活性空間視為一個多軌道塊。此時參考態波函數實際上簡化為

其中 i，j為占據自旋軌道指標。相應地，2T及更高階的激發算符也會簡化40。確定 CAS-BCCC4能量和各個激發振幅的方法與 SRCC類似，通過將Schr?dinger方程投影到參考波函數和各激發組態函數可分別得到如下的非線性方程組：

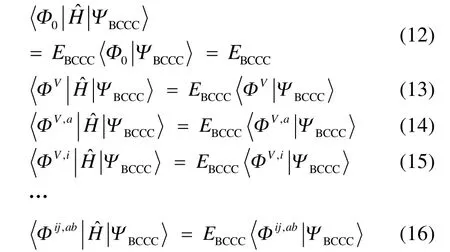
其中a，b為虛軌道指標，V為塊電子態指標，且

其他組態函數的定義以此類推。振幅迭代公式采用類似SRCC方法中Hirata和Bartlett提出的迭代公式47。顯然，上述公式的展開和化簡比相應 SRCC的公式要繁瑣得多，實際操作中相關公式通過采用計算機程序自動推導得出。由于電子的哈密頓算符中每一項至多只包含 4個單粒子算符(2個產生算符和2個湮滅算符)，所以將BCCC的簇激發算符截斷至4塊有其合理性：4塊以上的激發組態函數與參考態波函數沒有相互作用，對基態能量沒有直接貢獻。另外，CAS-BCCC4方法與單參考CCSD方法的緊密聯系還有以下四點：第一，當參考態中唯一的多軌道塊退化為一個自旋軌道時，CAS-BCCC4方程會相應地退化為CCSD方程。第二，從簇激發算符式(9)和(10)的形式可以看出，式(13)?(16)中的各個左矢波函數是各不相同的激發組態，不會出現相同的兩個左矢，即方程個數等于未知變量(即左矢波函數)數目，這點與CCSD方程一致。第三，單參考CCSD方法的計算標度為N6，其中N為體系電子數；當活性空間大小固定而體系增大時，CAS-BCCC4方法的計算標度也為N6，這已在此前的文獻40中詳細討論了。但是CAS-BCCC4方法比CCSD方法的標度“前因子”(prefactor)大，圖1中兩種方法分別計算不同碳數的鏈烷烴分子中單根碳碳鍵斷裂時基態能量的計算時間隨體系的增長情況可以反映出這一點(傳統 CCSD方法的計算采用 Gaussian 09軟件48)。第四，BCCC方法中各簇激發算符之間也是對易的，這點與CCSD的激發算符性質一樣。當然，還可以通過e-THeT的Hausdorff展開式將N能量方程(12)和振幅方程(13)?(16)解耦合，不過目前我們在程序自動推導公式和編程中還沒采取這種做法。而且我們的雙電子積分變換代碼沒有經過詳細地優化，這也是圖 1中同一體系CAS-BCCC4計算時間較 CCSD時間長得多的原因之一。不過這些不足不會影響結果的準確性，在描述甲烷分子中 C―H單鍵解離和雙原子分子N≡N三鍵的解離上，CAS-BCCC4方法已經十分接近完全組態相互作用(FCI)的結果(見表 1和圖2)，可以定量描述鍵解離勢能面。

常用非平行誤差(nonparallelism errors，NPE)來衡量計算相對能量的精度。從表 1可以看出，針對 CH4單鍵解離勢能面的計算，CAS-BCCC4給出的NPE值只有0.30 mH，說明該方法精度很高，且優于 MR-CISD。對 N≡N三鍵的解離，CAS-BCCC4方法對勢能面的描述優于 MR-CISD和CASPT2方法，其NPE值為2.33，稍微大一些，但仍比另外兩種方法要好不少(見圖2中NPE值的比較)。

如果一個理論方法能夠對鍵解離勢能面給予高精度的描述，則它一定可以用來獲得高精度的化學反應能壘。如圖 3所示，環丁烯的開環反應中，反應物分子經由一個雙自由基過渡態(TS)生成產物1,3-丁二烯，該TS具有明顯的多參考特征，傳統單參考方法一般難以得到可靠的描述。如圖4所示，比較 CASSCF、MR-CISD、CASPT2和CAS-BCCC4四種方法計算得到的反應物能量和反應能壘，可以發現對反應物分子的基態電子能量，CAS-BCCC4給出的結果比其他三種方法都要低；對于反應能壘，除了 CASSCF，其余方法結果均與實驗值((133.6 ± 0.8) kJ·mol?1)較為接近。總結CAS-BCCC4的特點：(1) 公式和理論框架十分接近 SRCC；(2) 計算量隨 CAS空間的增大而急劇上升，但活性空間固定時與傳統CCSD方法具有類似的計算標度；(3) 可以定量描述單鍵和多鍵的解離，精度高于CASPT2和MRCI方法。該方法的缺點也比較直觀：由于采用CASSCF波函數為參考態，只能應用于活性空間較小的體系，且不具備嚴格的大小一致性。

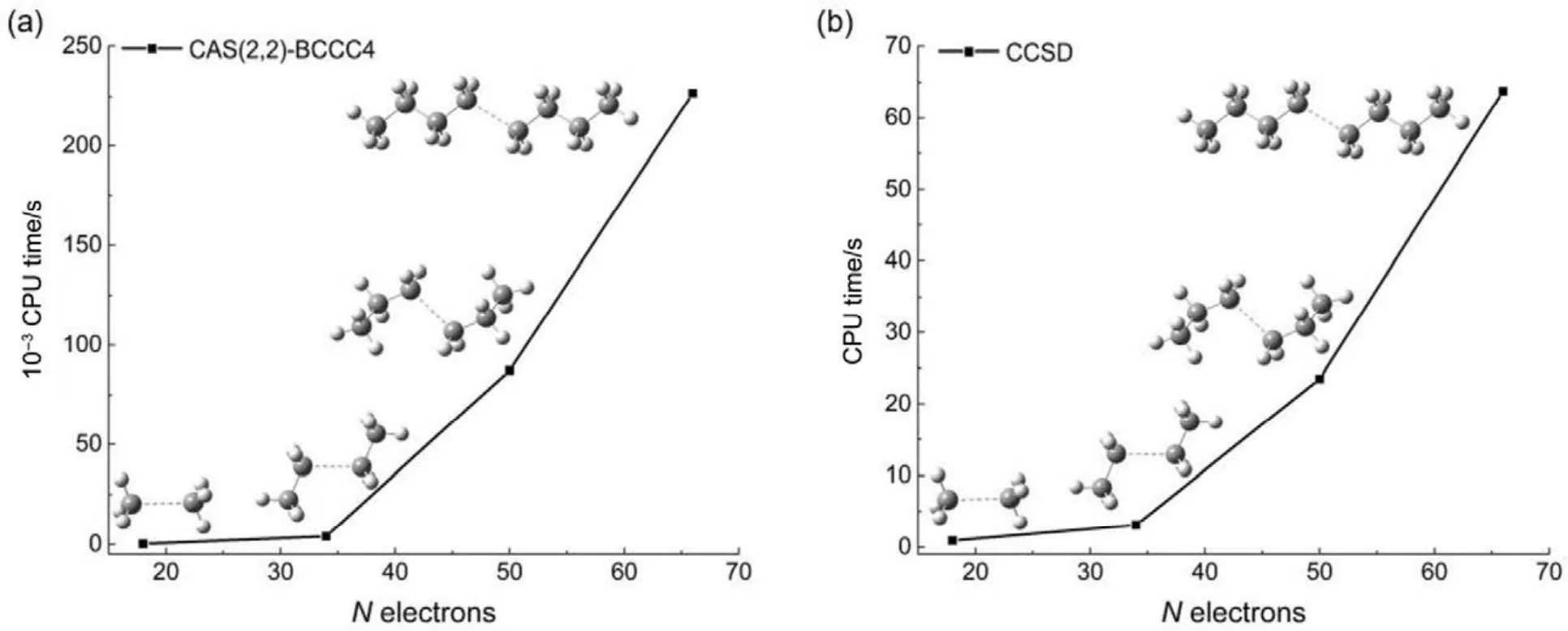
圖1 烷烴分子中單根碳碳鍵斷裂時CAS-BCCC4方法和CCSD方法計算體系基態能量的時間隨體系增大的變化情況Fig.1 CPU time of CAS(2,2)-BCCC4 and CCSD method in calculating bond breaking ground state energies of different sizes of alkanes.

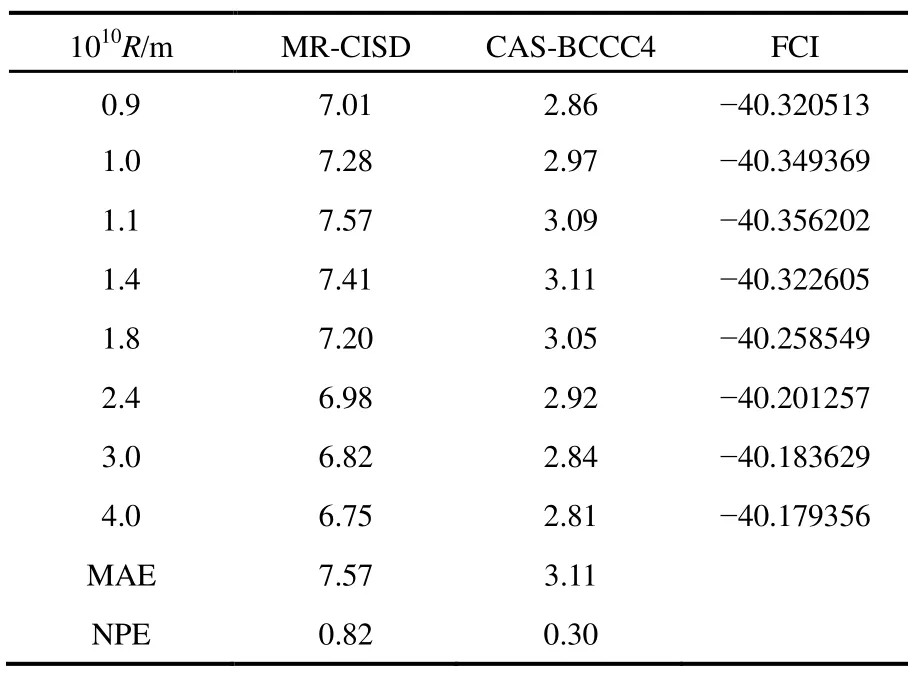
表1 CAS-BCCC4，MR-CISD和FCI三種方法計算甲烷分子中1根C―H鍵被拉長時基態電子能量的比較Table 1 Ground state energies calculated with CAS-BCCC4, MR-CISD and FCI methods for single C―H bond breaking in methane, at various bond distances.

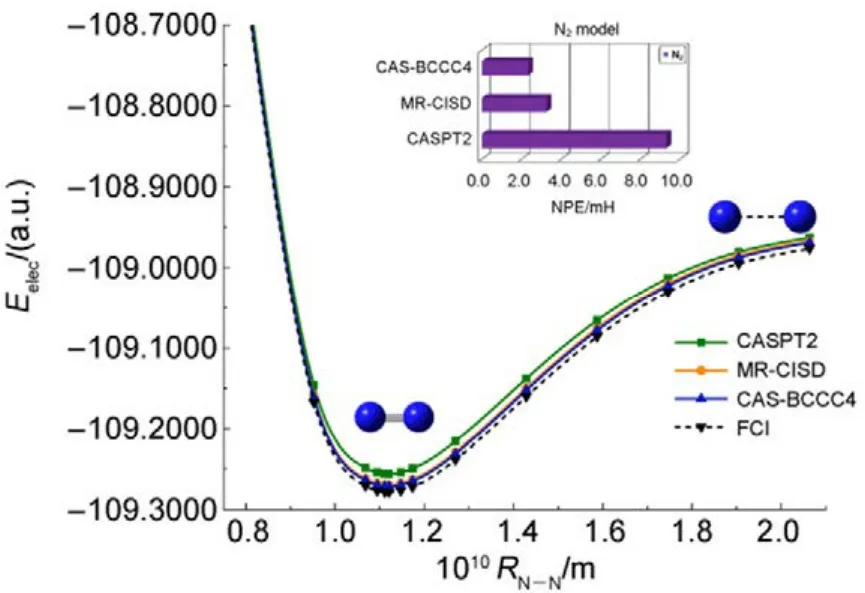
圖2 N2分子解離勢能面和能量精度比較Fig.2 Bond-breaking potential energy surface in N2.

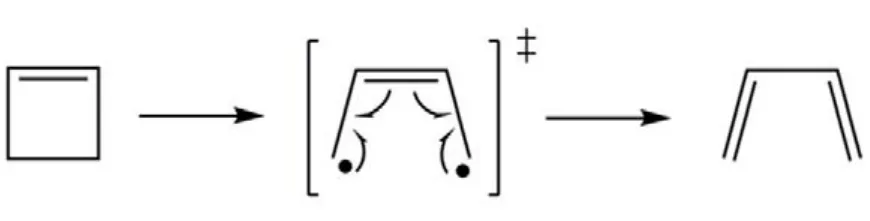
圖3 環丁烯的開環反應Fig.3 Ring-opening reaction of 1-cyclobutene.

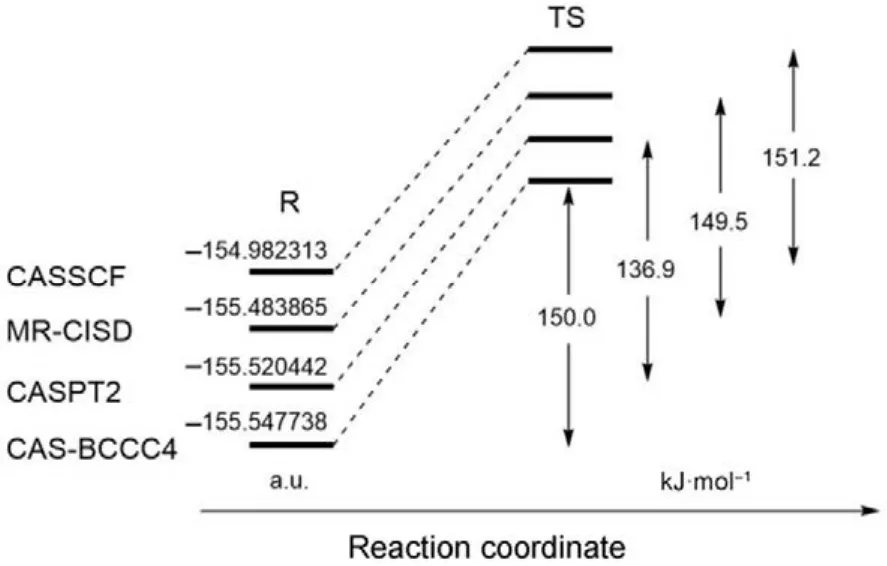
圖4 采用不同多參考方法計算環丁烯開環反應中反應物分子能量和反應能壘的比較Fig.4 Comparison of the ground-state energies of the reactant and reaction barriers calculated using various MR methods.

2.2 GVB-BCPT2方法

GVB-PP波函數46分為三個部分：閉殼層芯軌道，軌道對和高自旋開殼層軌道部分，在自然軌道表示下可以寫為式(19)和(20)的形式。其中為反對稱化算符，所有的φ均為空間軌道，(σpi1,σpi

2)為第i個軌道對的系數(pair coefficients)。自旋函數Θ = α(1)β(2)α(3)β(4)…αα…α，遍歷所有對和未成對電子。可以看出，上述波函數若展開可以表示為若干行列式的線性組合，因此GVB波函數帶有多參考特征，可以看成是CASSCF波函數的一種近似45。GVB-BCPT2方法將每個軌道對視為一個塊，利用激發算符將電子在塊內產生激發或直接激發至別的塊上，產生激發組態函數。塊激發算符的形式在以前的工作44中已經給出(注意與BCCC的簇激發算符不同)。零階波函數定義為每個塊的基態電子態的乘積，再選取零階哈密頓為各個塊哈密頓算符的加和，就可以使零階波函數為其本征函數，形式分別如下：其中指標r遍歷所有虛軌道，λ遍歷一個塊內所有可能的電子態， EPλ對應塊電子態的本征能量，由對角化塊哈密頓矩陣得到。由于GVB波函數的特殊性，除了成對軌道構成的塊是多軌道塊(包含 4個自旋軌道)，其他塊均為單軌道塊(占據自旋軌道或虛軌道)，則有了零階哈密頓，微擾算符即為 V? = H? - H?0，二階微擾能(不包括零階和一階能量)表達式為

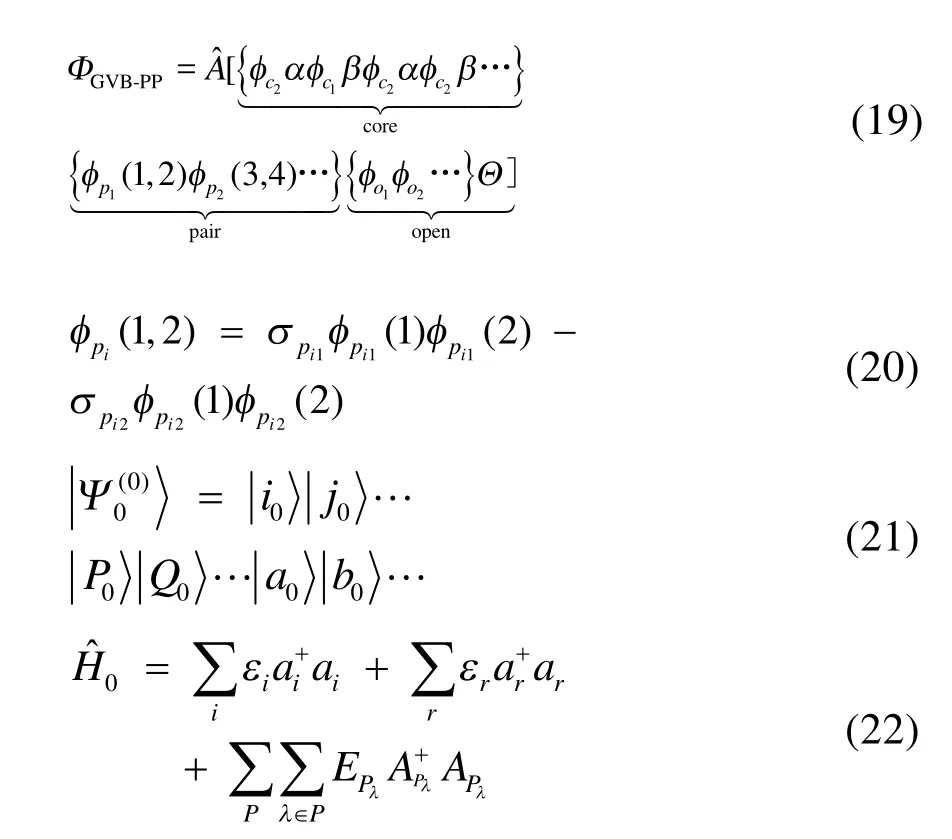
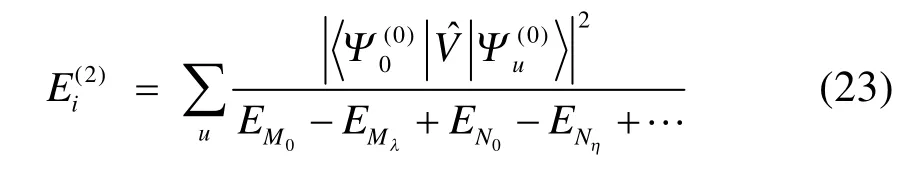
傳統 MP2方法的計算量為 N5；而在GVB-BCPT2方法中，當挑選的軌道對數目一定時，隨著體系電子數N的增加，該方法的計算標度也是N5級別44。但是同樣地，后者比前者的標度“前因子”要大，所以計算時間更長。圖 5中展示了兩種方法對不同碳數的鏈烷烴分子中一根C―C鍵和一根末端C―H鍵同時斷裂時基態能量的計算時間隨體系的增長情況，可以反映出這一點。可以預期，GVB-BCPT2方法的精度應該比MP2結果有所改善，但仍不如CASPT2。圖6中列出了三種方法計算雙原子分子振動光譜常數的結果，可以看出采用帶有多參考特征的GVB波函數作為參考態后，精度比MP2方法結果好，接近CASPT2的結果，符合理論預期。除此之外，GVB-BCPT2的明顯優勢還在于可以處理活性空間比CAS類方法大得多的體系。以一個強關聯模型線性長鏈H50為例，將所有H―H距離拉伸時，活性空間必須包含全部50個電子，其中的組態數目是天文數字；但GVB采用25個軌道對來描述，可得到定性正確的結果。現有的基于CASSCF參考態的MR方法(如CASPT2)無法處理這樣大的活性空間。圖7展示了三種不同方法計算的H50解離勢能面的NPE值(以DMRG方法為參考值標定)，很明顯MP2精度在定性上存在問題，GVB本身能夠給出相對合理的精度，而GVB-BCPT2對GVB約有50%的改善。

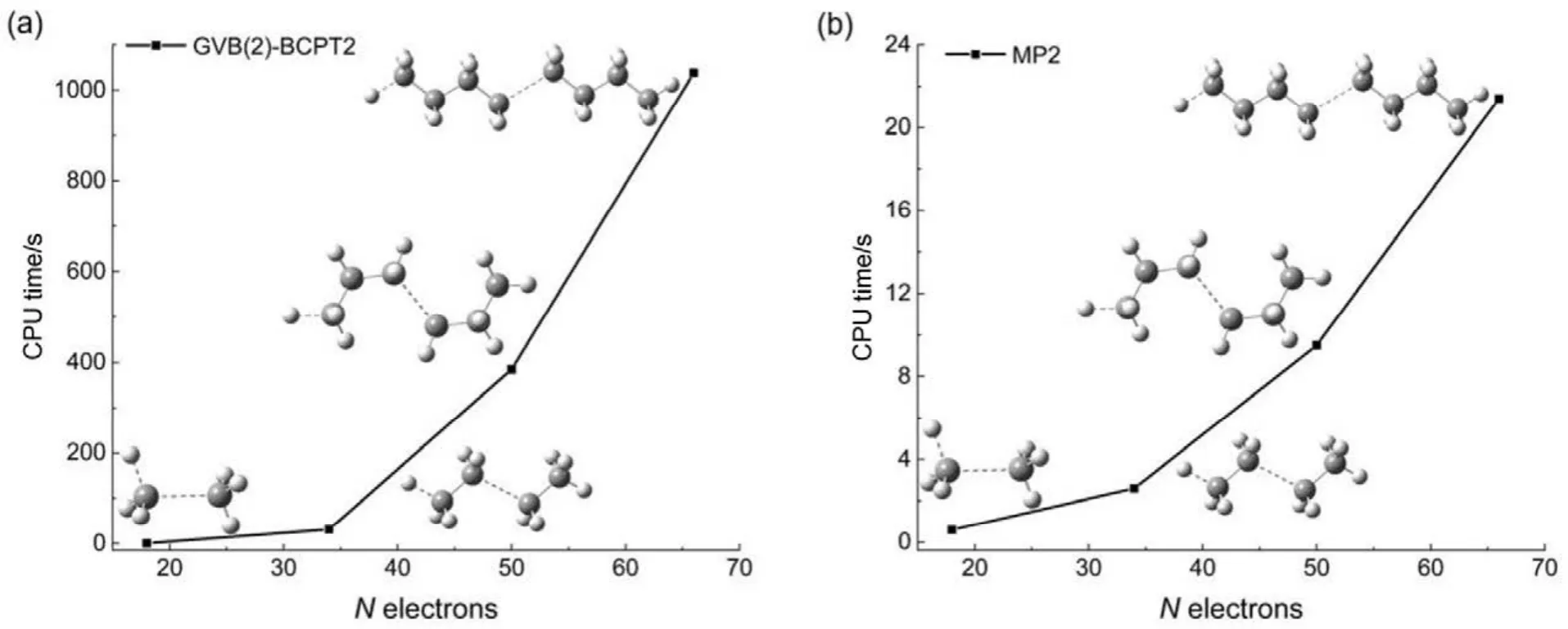
圖5 烷烴體系中C―C單鍵和C―H單鍵同時斷裂下GVB(2)-BCPT2和MP2方法計算基態能量的時間隨體系電子數的增長情況Fig.5 CPU time of GVB(2)-BCPT2 and MP2 method in calculating bond breaking ground state energies of different sizes of alkanes.

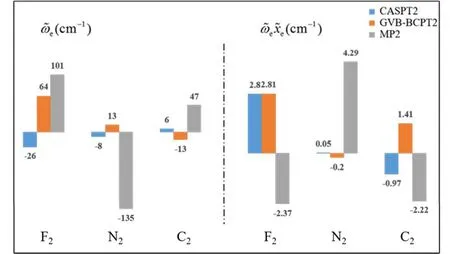
圖6 不同理論方法計算的幾種雙原子分子振動光譜常數與實驗值偏差的比較Fig.6 Deviations of computed spectroscopic constants with respect to experimental values for the ground state of several diatomic molecules.

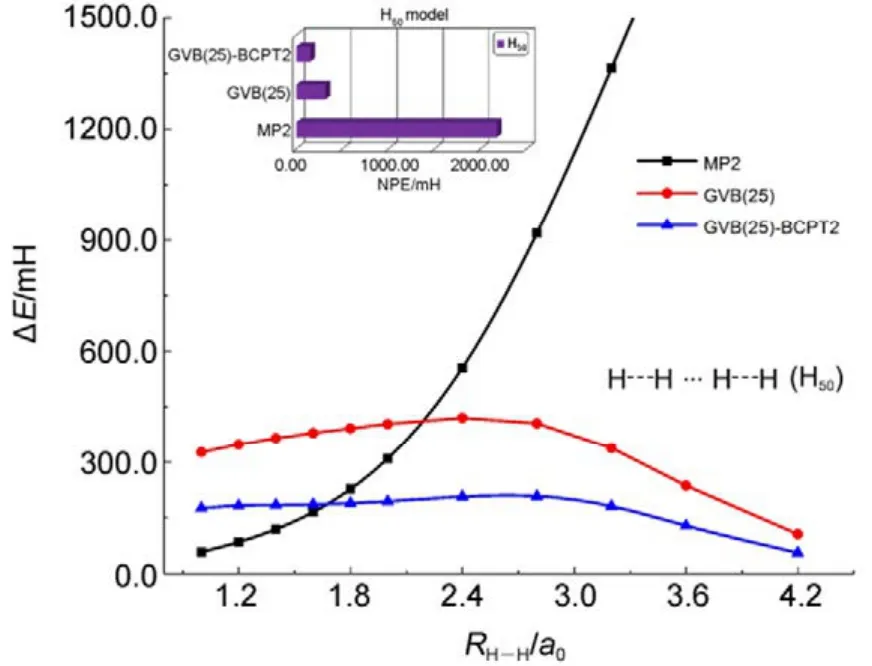
圖7 不同方法計算線性長鏈H50中所有鍵同時解離勢能面的精度Fig.7 Accuracy of different methods in calculating simultaneous bond dissociation potential energy surface in linear chain H50.

歸納GVB-BCPT2的優點：(1) 軌道對數目固定時，計算量類似于 MP2；(2) 可處理的活性空間大小超越基于CAS的MR方法。但是該方法也有缺點，對一些多鍵解離體系的計算結果表明GVB-BCPT2的能量無法收斂44,45，一個原因是存在一些軌道對的基態能量與激發組態能量非常接近(準簡并)，導致分母接近零而使結果誤差很大(MP2同樣有此問題)。可能的解決辦法是發展可高效考慮動態相關的GVB-BCCC4方法，我們課題組正在開展這方面的理論工作。

2.3 CASCI-BCPT2/GVB方法和

DMRG-BCPT2/GVB方法

如上所述，GVB-BCPT2方法不能處理多鍵解離的主要原因是微擾理論難以處理多鍵解離時幾個軌道對之間很強的動態相關。一個改進的思路是將強關聯的軌道對之間的電子相關用變分方法處理，而將軌道對與其它軌道之間的電子相關用GVB-BCPT2中類似的方法處理。CASCI-BCPT2/GVB45這種雜化方法正是基于這個思路，對CAS/A49方法的動態相關能用近似的方法計算。例如，CAS/A的能量表達式為

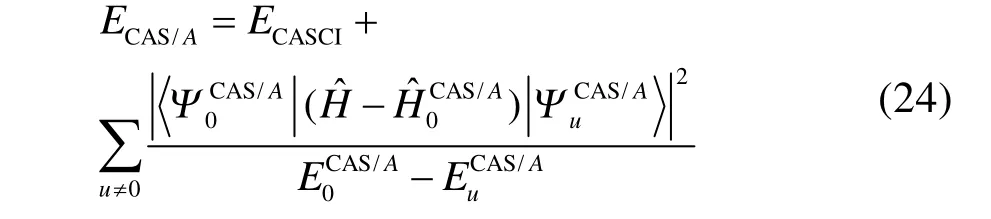
上述等式右邊第二項涉及動態相關，但由于CAS/A考慮了活性空間內所有可能的組態，只能應用于活性空間非常小的體系。若將其中的CASCI參考態替換為GVB參考態，對應的激發組態替換為 GVB-BCPT2中塊激發算符產生的激發組態，總能量簡化為如下形式

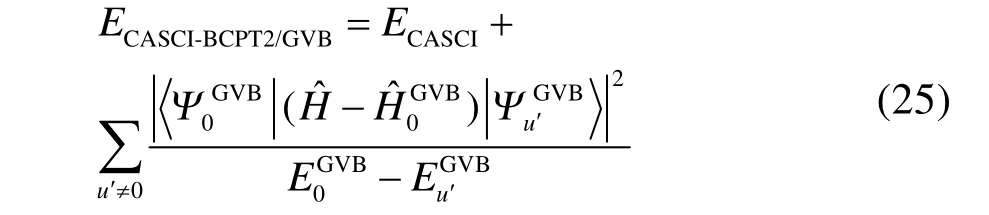
上式中右邊第二項相比式(24)中右邊第二項，計算量大大降低。此處有兩點需要說明：第一，在計算第二項的動態相關時，求和項中不包括軌道對之間激發算符產生的激發組態，因為這部分的貢獻已經包含在第一項中；第二，式(24)中求和指標u是遍歷活性空間內所有的激發組態；而式(25)中求和指標u′是遍歷各軌道對內激發組態，通過多個低激發算符的乘積可以耦合出高激發組態，從而在CAS/A中的高激發組態對應矩陣元的計算簡化為在 GVB-BCPT2中若干個低激發組態對應矩陣元的乘積，即矩陣元的計算大大簡化，故而計算量降低。將上式中的 ECASCI替換為密度矩陣重整化群(density matrix renormalization group，DMRG)參考態的能量 EDMRG，即得到DMRG-BCPT2/GVB方法45的總能量定義式。這兩種雜化方法中，前者可以看作是對CAS/A方法的近似，后者則可以視為對單純的DMRG方法的改進。不過，這種“雜化”式的改進與近年來發展的直接基于DMRG參考態波函數，再引入外部動態相關的密度矩陣重整化群-活性空間二階微擾(DMRG-CASPT2)50、密度矩陣重整化群-正則變換(DMRG-CT)51、密度矩陣重整化群-強簡縮N電子價態二階微擾(DMRG-SC-NEVPT2)52和矩陣乘積態-線性化耦合簇(MPS-LCC)53等等“純”post-DMRG方法又有不同：DMRG-BCPT2/GVB方法的靜態相關項是由 DMRG參考態獲得的，而其動態相關項是用GVB參考態去近似得出的；但是上述幾種 post-DMRG方法不僅靜態相關能由DMRG獲得，其動態相關能也是直接在DMRG參考態基礎上作激發得到的。當然，這些post-DMRG方法與我們的方法異曲同工，都能處理活性空間大得多的體系。例如，過渡金屬雙原子分子Cr2定量正確的解離勢能面已經有DMRG-CASPT2(12,28)50和DMRG-SC-NEVPT2(12,22)方法52報道過了。

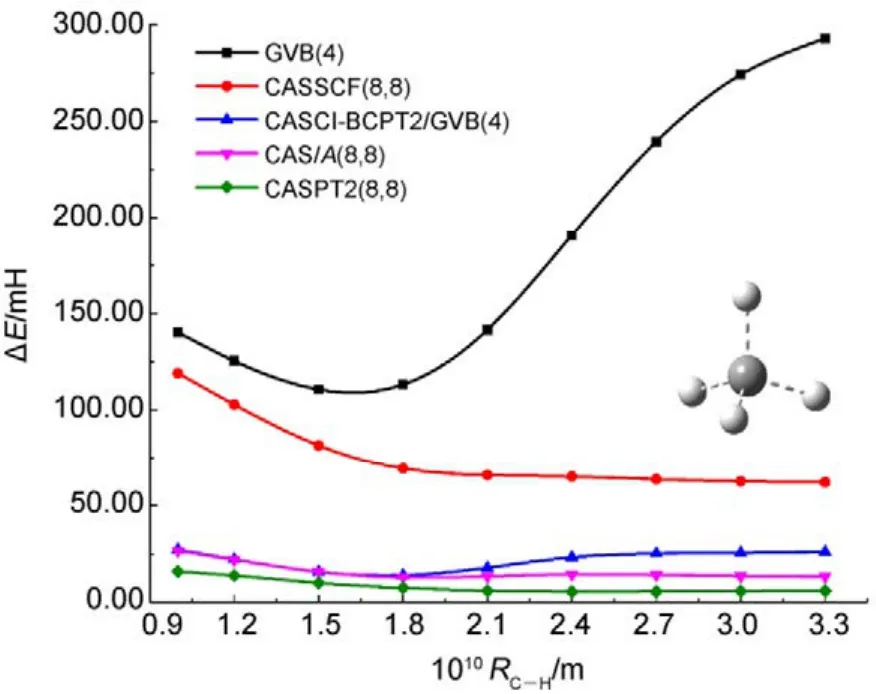
圖8 不同方法計算甲烷分子中所有單鍵同時解離的勢能面Fig.8 Potential energy surfaces for simultaneous bond dissociation in CH4, calculated with various methods.

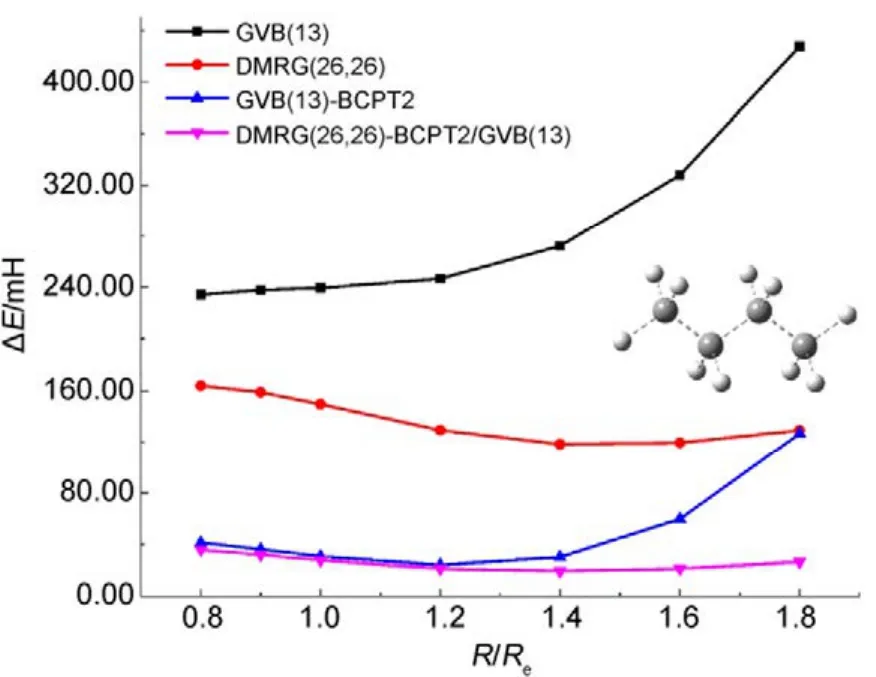
圖9 不同方法計算正丁烷分子中所有單鍵同時解離的勢能面Fig.9 Potential energy surfaces for simultaneous bond dissociation in n-butane, calculated with various methods.

圖8和圖9中列出了分別使用兩種方法計算CH4和正丁烷(C4H10)分子中所有單鍵同時解離的勢能面。如圖 8所示，CASCI-BCPT2/GVB與CAS/A計算的電子能量和精度均非常接近(NPE分別為13.20和13.87)，比單純的GVB或CASSCF的結果要好很多。當然，CASPT2的精度更高。但如前所述，CASPT2計算量更大，處理CH4中4根單鍵同時斷裂的活性空間尚合適，處理 C4H10分子中13根單鍵同時解離時則不適用，因為此時需要 CASSCF(26,26)作為參考波函數。這時可以采用DMRG-BCPT2/GVB方法，GVB參考態則選為GVB(13)，即包含13個軌道對。從圖9可看出，GVB(13)-BCPT2給出的精度已經不如單純的DMRG(26,26)方法，而 DMRG(26,26)-BCPT2/GVB(13)對 DMRG(26,26)的結果又可以有超過60%的改善(相對于非常精確的DMRG(26,52)的結果)，說明該方法描述動態相關是比較有效的。以上的結果表明基于 GVB參考態的CASCI-BCPT2/GVB或DMRG-BCPT2/GVB能夠在 GVB基礎上比較有效地描述動態相關能。然而，當研究體系的軌道局域化程度較差時，GVB波函數便不太適合用作參考態，此時用這兩種方法所得的計算精度會有所下降，一些體系的計算結果45已經驗證了這種問題的存在。

3 結 論

本文詳細介紹了在塊相關理論框架下塊相關微擾理論和塊相關耦合簇理論的基本思想和相關的理論公式。塊的概念是整個塊相關理論框架的基石：將若干個自旋軌道視為整體，即一個塊，電子相關問題轉化為塊相關問題，體系的零階波函數寫為各個塊最重要電子態的張量積，激發組態的構建采用塊內或塊間電子的激發，由此便可自然地發展出塊相關微擾理論和塊相關耦合簇理論。這兩種多參考理論在公式和計算標度上類似于傳統的單參考理論，具有其他多參考方法難以替代的優點。以 CASSCF波函數為參考態，CAS-BCCC4方法可以定量描述單鍵和多重鍵的解離，十分接近 FCI的結果，但只能處理較小的活性空間。以 GVB 波函數為參考態的GVB-BCPT2方法能夠處理體系中許多單鍵的同時解離，所涉及的活性空間大小超越常規多參考方法(如CASPT2)的極限，但精度有所下降，不如CASPT2。而在GVB-BCPT2的基礎上，兩種改良方案CASCI-BCPT2/GVB和DMRG-BCPT2/GVB方法可以對中等大小活性空間的體系給出優于GVB-BCPT2的描述，大幅提高了計算精度。但無論是這兩種改良方法，還是適合較小活性空間的更高精度的 CAS-BCCC4方法，都不意味著塊相關理論的能力極限。相反，基于塊相關理論處理多參考問題的巨大潛力，相信未來會發展出適用大活性空間的高精度塊相關電子結構新方法。

4 展 望

近二三十年高精度電子結構方法的發展表明，單參考電子相關方法已經成熟，黑箱式的程序已經可讓用戶很方便地使用。當HF行列式是合適的參考態時，單參考方法能給出令人滿意的結果。但是對具有多參考特征的體系，如何以稍大于單參考方法的計算量來給出定量正確的結果，并盡量減少運行程序時的人為干預，仍然是今后多參考方法研究的重點和難點。對于MRPT理論，一方面需要繼續尋找符合大小一致性的微擾理論框架；另一方面，發展更高階的微擾理論同時盡量確保總能量隨微擾項的增加而改善，也是一個很有挑戰性的方向。而對于MRCC理論，直接以CASSCF為參考態的多參考方法面臨無法處理較大活性空間的難題，發展以更緊湊形式表示組態、更有效考慮激發組態的理論方法十分誘人；發展基于UHF、GVB和APSG(antisymmetric product of strongly orthogonal geminals)54,55等參考波函數的“另類”MRPT和MRCC方法也許是一條擴大可處理活性空間的有效途徑。在應用方面，定量描述分子的激發態和雙(或多)自由基反應的能壘、理論模擬各種分子光譜(如IR、Raman和NMR譜等)和處理凝聚相或周期性體系等熱點問題也勢必將成為多參考方法大顯身手的舞臺。

致 謝:文中部分計算在南京大學高性能計算中心完成。

(1) Lyakh, D. I.; Musia?, M.; Lotrich, V. F.; Bartlett, R. J. Chem. Rev.2012, 112 (1), 182. doi: 10.1021/cr2001417

(2) W?och, M.; Gour, J. R.; Piecuch, P. J. Phys. Chem. A 2007, 111 (44),11359. doi: 10.1021/jp072535l

(3) Bartlett, R. J. WIREs Comput. Mol. Sci. 2012, 2 (1), 126.doi: 10.1002/wcms.76

(4) Amos, R. D.; Andrews, J. S.; Handy, N. C.; Knowles, P. J. Chem.Phys. Lett. 1991, 185 (3–4), 256.doi: 10.1016/S0009-2614(91)85057-4

(5) Murray, C.; Davidson, E. R. Chem. Phys. Lett. 1991, 187 (5), 451.doi: 10.1016/0009-2614(91)80281-2

(6) Jayatilaka, D.; Lee, T. J. J. Chem. Phys. 1993, 98 (12), 9734.doi: 10.1063/1.464352

(7) Szalay, P. G.; Gauss, J. J. Chem. Phys. 1997, 107 (21), 9028.doi: 10.1063/1.475220

(8) Chen, F. J. Chem. Theory Comput. 2009, 5 (4), 931.doi: 10.1021/ct800546g

(9) Wheeler, S. E.; Allen, W. D.; Schaefer, H. F. J. Chem. Phys. 2008,128 (7), 074107. doi: 10.1063/1.2828523

(10) Krylov, A. I. J. Chem. Phys. 2000, 113 (15), 6052.doi: 10.1063/1.1308557

(11) Chen, F. W.; Wei, M. J.; Liu, W. J. Sci. China Chem. 2011, 54 (3),446. doi: 10.1007/s11426-010-4199-1

(12) Andersson, K.; Malmqvist, P. ?.; Roos, B. O. J. Chem. Phys. 1992,96 (2), 1218. doi: 10.1063/1.462209

(13) Sinha Mahapatra, U.; Datta, B.; Mukherjee, D. J. Phys. Chem. A 1999, 103 (12), 1822. doi: 10.1021/jp9832995

(14) Chattopadhyay, S.; Chaudhuri, R. K.; Mahapatra, U. S.; Ghosh, A.;Ray, S. S. WIREs Comput. Mol. Sci. 2016, 6 (3), 266.doi: 10.1002/wcms.1248

(15) Jeziorski, B.; Monkhorst, H. J. Phys. Rev. A 1981, 24 (4), 1668.doi: 10.1103/PhysRevA.24.1668

(16) Meissner, L.; Jankowski, K.; Wasilewski, J. Int. J. Quantum Chem.1988, 34 (6), 535. doi: 10.1002/qua.560340607

(17) Balková, A.; Kucharski, S. A.; Meissner, L.; Bartlett, R. J. Theor.Chim. Acta 1991, 80 (4), 335. doi: 10.1007/bf01117417

(18) Li, X.; Paldus, J. J. Chem. Phys. 2003, 119 (11), 5320.doi: 10.1063/1.1599283

(19) Hanrath, M. J. Chem. Phys. 2005, 123 (8), 084102.doi: 10.1063/1.1953407

(20) Offermann, R.; Ey, W.; Kümmel, H. Nucl. Phys. A 1976, 273 (2), 349.doi: 10.1016/0375-9474(76)90596-0

(21) Offermann, R. Nucl. Phys. A 1976, 273 (2), 368.doi: 10.1016/0375-9474(76)90597-2

(23) Kutzelnigg, W. J. Chem. Phys. 1982, 77 (6), 3081.doi: 10.1063/1.444231

(24) Hughes, S. R.; Kaldor, U. Chem. Phys. Lett. 1992, 194 (1), 99.doi: 10.1016/0009-2614(92)85749-Z

(25) Meissner, L.; Malinowski, P. Phys. Rev. A 2000, 61 (6), 062510.doi: 10.1103/PhysRevA.61.062510

(26) Huba?, I.; Neogrády, P. Phys. Rev. A 1994, 50 (6), 4558.doi: 10.1103/PhysRevA.50.4558

(27) Má?ik, J.; Huba?, I.; Mach, P. J. Chem. Phys. 1998, 108 (16), 6571.doi: 10.1063/1.476071

(28) Mahapatra, U. S.; Datta, B.; Bandyopadhyay, B.; Mukherjee, D. In Advances in Quantum Chemistry, Per-Olov, L., Ed.; Academic Press:San Diego, CA, 1998; Vol. 30, pp 163. doi:10.1016/S0065-3276(08)60507-9

(29) Mahapatra, U. S.; Datta, B.; Mukherjee, D. J. Chem. Phys. 1999, 110(13), 6171. doi: 10.1063/1.478523

(30) Chattopadhyay, S.; Pahari, D.; Mukherjee, D.; Mahapatra, U. S. J.Chem. Phys. 2004, 120 (13), 5968. doi: 10.1063/1.1650328

(31) K?hn, A.; Hanauer, M.; Mück, L. A.; Jagau, T.-C.; Gauss, J. WIREs Comput. Mol. Sci. 2013, 3 (2), 176. doi: 10.1002/wcms.1120

(32) Lyakh, D. I.; Ivanov, V. V.; Adamowicz, L. J. Chem. Phys. 2005, 122(2), 024108. doi: 10.1063/1.1824897

(33) Lyakh, D. I.; Ivanov, V. V.; Adamowicz, L. Mol. Phys. 2007, 105(10), 1335. doi: 10.1080/00268970701332539

(34) Li, X.; Paldus, J. J. Chem. Phys. 1997, 107 (16), 6257.doi: 10.1063/1.474289

(35) Li, X.; Paldus, J. Mol. Phys. 2000, 98 (16), 1185.doi: 10.1080/00268970050080546

(36) Li, X.; Paldus, J. J. Chem. Phys. 2006, 124 (17), 174101.doi: 10.1063/1.2194543

(37) Li, X.; Paldus, J. J. Chem. Phys. 2006, 125 (16), 164107.doi: 10.1063/1.2361295

(38) Li, X.; Paldus, J. J. Chem. Phys. 1998, 108 (2), 637.doi: 10.1063/1.475425

(39) Li, S. J. Chem. Phys. 2004, 120 (11), 5017. doi: 10.1063/1.1646355

(40) Fang, T.; Li, S. J. Chem. Phys. 2007, 127 (20), 204108.doi: 10.1063/1.2800027

(41) Fang, T.; Shen, J.; Li, S. J. Chem. Phys. 2008, 128 (22), 224107.doi: 10.1063/1.2939014

(42) Shen, J.; Fang, T.; Hua, W.; Li, S. J. Phys. Chem. A 2008, 112 (20),4703. doi: 10.1021/jp7118907

(43) Shen, J.; Fang, T.; Li, S.; Jiang, Y. J. Phys. Chem. A 2008, 112 (48),12518. doi: 10.1021/jp807183m

(44) Xu, E.; Li, S. J. Chem. Phys. 2013, 139 (17), 174111.doi: 10.1063/1.4828739

(45) Xu, E.; Zhao, D.; Li, S. J. Chem. Theory Comput. 2015, 11 (10),4634. doi: 10.1021/acs.jctc.5b00495

(46) Bobrowicz, F. W.; Goddard, W. A. In Methods of Electronic Structure Theory; Schaefer, H. F. Ed.; Springer US: Boston, MA, 1977; p 79.doi: 10.1007/978-1-4757-0887-5_4

(47) Hirata, S.; Bartlett, R. J. Chem. Phys. Lett. 2000, 321 (3–4), 216.doi: 10.1016/S0009-2614(00)00387-0

(48) Frisch, M. J. T., G. W.; Schlegel, H. B.; et al. Gaussian 09, Revision B.01, Gaussian Inc.: Wallingford, CT, 2009.

(49) Dyall, K. G. J. Chem. Phys. 1995, 102 (12), 4909.doi: 10.1063/1.469539

(50) Kurashige, Y.; Yanai, T. J. Chem. Phys. 2011, 135 (9), 094104.doi: 10.1063/1.3629454

(51) Yanai, T.; Kurashige, Y.; Neuscamman, E.; Chan, G. K. L. J. Chem.Phys. 2010, 132 (2), 024105. doi: 10.1063/1.3275806

(52) Guo, S.; Watson, M. A.; Hu, W.; Sun, Q.; Chan, G. K.-L. J. Chem.Theory Comput. 2016, 12 (4), 1583. doi: 10.1021/acs.jctc.5b01225

(53) Sharma, S.; Alavi, A. J. Chem. Phys. 2015, 143 (10), 102815.doi: 10.1063/1.4928643

(54) Zoboki, T.; Szabados, á.; Surján, P. R. J. Chem. Theory Comput.2013, 9 (6), 2602. doi: 10.1021/ct400138m

(55) Jeszenszki, P.; Nagy, P. R.; Zoboki, T.; Szabados, á.; Surján, P. R. Int.J. Quantum Chem. 2014, 114 (16), 1048. doi: 10.1002/qua.24634

Multireference Perturbation Theory and Multireference Coupled Cluster Theory Based on the “Block-Correlation” Framework

ZOU Jing-Xiang1SHEN Jun2XU En-Hua3FANG Tao1LI Shu-Hua1,*
(1School of Chemistry and Chemical Engineering, Key Laboratory of Mesoscopic Chemistry of Ministry of Education, Institute of Theoretical and Computational Chemistry, Nanjing University, Nanjing 210023, P. R. China;2Department of Chemistry,Michigan State University, East Lansing, Michigan 48824, United States;3Graduate School of System Informatics,Kobe University, Kobe, Hyogo 657-0025, Japan)

Well-developed conventional single-reference electron-correlation methods usually fail to describe the dissociation of covalent bonds, di(or poly)radical systems or electronic structures of the excited states. Based on a multi-determinantal wave function, recently emerged multireference perturbation theories and coupled cluster theories can give drastically improved results; however, there is still no satisfactory scheme so far. In this monograph, alternative multireference perturbation theories and coupled cluster theories based on the “block-correlation” framework has been introduced and illustrated in detail, together with proper comparisons with other common electron-correlation methods. Future perspectives upon multireference theories have also been briefly discussed.

Multireference; Block-correlated perturbation theory; Block-correlated coupled cluster theory; Multiple bond dissociation; Energy potential surface

December 1, 2016; Revised: March 21, 2017; Published online April 7, 2017.

O641.12

10.1016/0375-9474(78)90068-4

[Feature Article]

10.3866/PKU.WHXB2017040702 www.whxb.pku.edu.cn

*Corresponding author. Email: shuhua@nju.edu.cn; Tel: +86-25-89686465.

The project was supported by the National Natural Science Foundation of China (21333004, 21673110).國家自然科學基金(21333004, 21673110)資助項目

? Editorial office of Acta Physico-Chimica Sinica

鄒競祥，南京大學化學化工學院物理化學專業博士研究生。2015年于南京大學匡亞明學院獲理學學士學位。主要研究興趣為多參考態耦合簇理論和化學反應機理的自動化搜索。

沈軍，2008年于南京大學化學化工學院獲理學博士學位。2010年至今于美國密歇根州立大學工作，現為該校化學系研究助理。主要研究方向為高精度電子相關方法的發展及應用。

方濤，2008年于南京大學化學化工學院獲理學博士學位。2008?2012年在日本量子化學研究所工作。主要研究方向包括多參考態耦合簇理論和大分子體系的分片方法。

許恩華，2011年于南京大學化學化工學院獲理學博士學位。現于日本神戶大學從事博士后研究工作，主要研究方向為多參考態微擾理論和多參考態耦合簇理論。

黎書華，南京大學教授，博士生導師，教育部“長江學者”特聘教授，2014年當選世界理論與計算化學家協會理事會理事。主要研究領域為線性標度量子化學計算方法、多參考態電子相關方法和無機及有機金屬反應的理論研究。