一種基于加權平均的改進型小波閾值降噪算法①

劉書俊 李生林 蔣 明 宋志強 畢金友

(1.中國人民解放軍后勤工程學院；2.76166部隊)

一種基于加權平均的改進型小波閾值降噪算法①

劉書俊1李生林1蔣 明1宋志強1畢金友2

(1.中國人民解放軍后勤工程學院；2.76166部隊)

通過分析傳統硬、軟閾值小波降噪算法的原理和特點，提出一種改進型小波閾值降噪算法。該算法基于加權平均原理，結合了硬、軟閾值降噪的優點，克服了硬閾值函數在閾值處不連續的缺點，使重構信號具有更加良好的光滑度；同時克服了軟閾值函數存在固定偏差的不足，提高了重構精度，優勢明顯。通過實驗對傳統硬、軟閾值小波降噪算法與改進型小波閾值降噪算法進行了對比分析，結果表明：改進型小波閾值降噪算法的降噪效果更好，信噪比更高，均方根誤差更小。

小波閾值降噪 磁記憶檢測 加權平均 硬、軟閾值

在信號處理領域，小波變換是一種全新的分析方法，具有良好的時頻局部化特性，即在低頻部分具有較高的頻率分辨率和較低的時間分辨率，而在高頻部分具有較高的時間分辨率和較低的頻率分辨率[1,2]。由于小波可以提供一個隨頻率改變的“時間-頻率”窗口，是信號處理的理想工具，因此也被譽為“數學顯微鏡”[3]。由于真實信號和噪聲的小波系數在不同尺度上具有不同的性質，因此，小波閾值降噪實際上就是根據先驗性知識，進一步構造相應的處理規則，最后在小波域采取相應的數學處理方法對含噪信號的小波系數加以處理[4,5]。在實踐中，以Donoho提出的硬、軟閾值小波降噪算法應用最廣[6]，該算法原理簡單、計算量小，但由于它自身存在缺陷，降噪效果還不夠理想。因此，筆者提出一種基于加權平均原理的改進型小波閾值降噪算法。

1 硬、軟閾值小波降噪算法

1.1 算法原理

在硬、軟閾值小波降噪算法中，軟閾值函數為：

(1)

硬閾值函數為：

(2)

式中T——系數處理的閾值；

Wj,k——含噪信號經過小波變換后的小波系數；

圖1、2分別為硬、軟閾值函數圖形，其中x表示閾值化處理之前的小波系數，y表示經過閾值化處理的小波系數。

圖1 硬閾值函數

圖2 軟閾值函數

硬、軟閾值方法自身具有一定的優點，但仍然存在一些缺陷：雖然軟閾值算法處理的小波系數整體連續、光滑性好，但對于大于閾值的小波系數采取恒定壓縮的方式，自然會損失一些有用的高頻信息，從而影響重構信號的真實性；硬閾值算法可以避免軟閾值的恒定偏差，但是由于小波系數在閾值T處是不連續的，這不可避免地會給重構信號帶來一些附加振蕩，使重構后信號的光滑度變差。因此，如果直接使用軟閾值或硬閾值函數對信號進行降噪處理，可能無法獲得理想的降噪效果[7,8]。

1.2 閾值函數的改進

為了有效彌補以上方法的不足，在硬、軟閾值的基礎上對閾值函數進行改進，引入權重指標，使用加權平均法，將硬、軟閾值函數用加權平均的方法結合起來。令閾值函數為：

(3)

其中，α=ab；b=-(|Wj,k|-T)2/n2；α為加權因子；a和n為常數，且a>1，a是一個與信號有關的常數，可通過實驗確定。

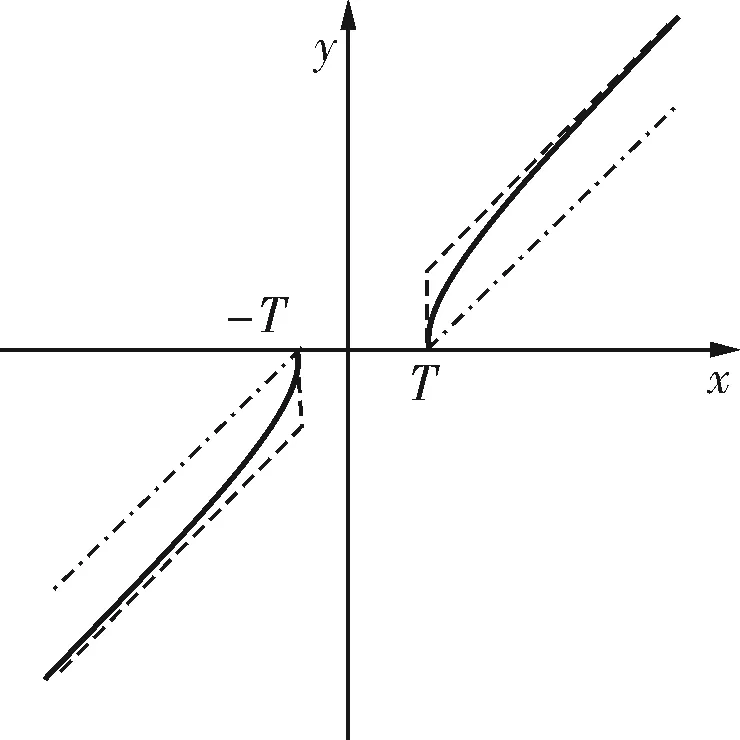
圖3 改進后的閾值函數

2 算法驗證

采用MFL-4032漏磁/磁記憶檢測儀對一段長1 000mm的管道進行磁記憶檢測[9]，為簡化試驗過程，采用雙通道磁記憶檢測探頭進行檢測。該管道共有9處裂紋，分別位于L1=136mm、L2=181mm、L3=322mm、L4=372mm、L5=526mm、L6=569mm、L7=752mm、L8=776mm、L9=959mm處。檢測所得原始信號如圖4所示，圖5為相應的梯度曲線。

圖4 檢測信號曲線

圖5 信號梯度曲線

根據俄羅斯動力診斷公司關于應力集中區或缺陷的判定準則[10,11]，對比分析檢測信號曲線改變符號且過零點和曲線梯度值極大值，由于信號被噪聲干擾，檢測信號曲線存在較多峰值毛刺，嚴重影響對信號過零點的標示；同時，由于該磁記憶信號本身較為復雜，包含較多的噪聲成分，此時的曲線梯度變化實際上不能反映真實的磁記憶信號梯度變化趨勢，在這種情況下，梯度曲線本身也就失去了分析的意義。因此，由于噪聲的干擾，導致無法根據應力集中區或缺陷的判定準則對應力集中位置或缺陷位置進行判定。

2.1 硬、軟閾值小波降噪效果分析

將信號進行硬、軟閾值小波降噪，由于軟閾值降噪效果與硬閾值降噪效果基本相同，此處僅以軟閾值為例進行說明。

圖6、7分別為圖4所示的磁記憶檢測信號經過小波軟閾值降噪后的曲線和相應的梯度曲線，其中，小波函數選用DB2小波，分解層數J=3。觀察磁場強度法向分量Hp(y)，基于小波軟閾值的磁記憶信號降噪可以消除部分噪聲的影響，磁記憶信號曲線峰值毛刺大量減少，可以明顯地看出曲線在L為181、371、529、565mm處過零點，在上述位置，磁記憶信號的梯度值也存在極大值，因此根據磁記憶檢測判定準則，可以初步判定鋼管以上位置存在應力集中或缺陷。但在100～150mm、315～330mm、725～800mm、925～970mm處，可以很明顯地看出，由于采用的降噪算法存在局限性，導致降噪效果不夠理想，磁記憶信號仍然存在峰值毛刺的干擾，光滑度不好，從而導致無法進一步對應力集中或缺陷位置進行判定。

圖6 軟閾值降噪后信號曲線

圖7 軟閾值降噪后信號梯度曲線

2.2 改進型算法降噪效果分析

采用改進型算法對信號進行降噪，得到降噪后的信號曲線和梯度曲線如圖8、9所示。

圖8 改進型算法降噪后信號曲線

圖9 改進型算法降噪后信號梯度曲線

對比采用軟閾值降噪后的信號曲線及其梯度曲線(圖6、7)，可以看出，改進型算法降噪效果明顯優于小波閾值降噪。磁記憶信號經過改進型降噪后，波形平滑，基本消除了峰值毛刺的干擾，無相位失真和信號損失，有效抑制了噪聲，信號梯度變化也可以很好地指示鋼管應力集中區域。根據俄羅斯動力診斷公司的定性判斷應力集中規則，磁記憶信號曲線在L為136、181、324、371、529、565、750、777、958mm處過零點，在上述位置，磁記憶信號曲線的梯度值K均存在極大值。因此，根據磁記憶判定準則，很容易判定管道在上述位置存在應力集中或缺陷，考慮到檢測誤差等人為因素的影響，這樣的檢測結果與實際情況是基本吻合的。

信號降噪效果可以采用信噪比(SNR)和均方根誤差(RMSE)來評價[12]。其中：

(4)

(5)

式中N——信號采樣點數；

s(n)——降噪前信號；

軟閾值算法和改進型算法的信噪比與均方根誤差對比見表1。可以看出，改進型算法的信噪比和均方根誤差指標均優于軟閾值算法，具有明顯的優勢。

表1 兩種降噪算法的性能指標對比 dB

3 結束語

基于加權平均的改進型小波閾值降噪算法，結合了硬、軟閾值降噪算法的優點，用MFL-4032漏磁/磁記憶檢測儀對一段長1 000mm的管道進行磁記憶檢測，結果表明：改進型算法克服了硬閾值函數在閾值處不連續的缺點，使重構信號具有更加良好的光滑度；同時克服了軟閾值函數存在固定偏差的不足，提高了重構精度。改進型算法的降噪效果顯著，并且提高了降噪后信號的信噪比，減少了信號的失真與振蕩。

[1] 張建,楊娜,鄭修凱,等.高速列車經過時跨線天橋表面風壓小波分析[J].振動與沖擊,2015,34(4):53～58.

[2] 郭健,查呂應,龐有超,等.基于小波分析的深基坑地表沉降預測研究[J].巖土工程學報,2014,36(z2):343～347.

[3] 李力,魏偉,唐汝琪,等.基于改進S變換的煤巖界面超聲反射信號處理[J].煤炭學報,2015,40(11):2580～2586.

[4] 李明,陳衛忠,楊建平.隧道結構在線監測數據分析方法研究[J].巖土力學,2016,37(4):1208～1216.

[5] 曲巍崴,高峰.基于噪聲方差估計的小波閾值降噪研究[J].機械工程學報,2010,46(2):28～33.

[6] 蘇文勝,王奉濤,朱泓,等.雙樹復小波域隱Markov樹模型降噪及在機械故障診斷中的應用[J].振動與沖擊,2011,30(6):47～52.

[7] 魏振春,王婿,徐娟.基于改進閾值自適應冗余小波的振動信號去噪[J].計算機仿真,2014,31(11):192～197.

[8] 賀巖松,劉程,徐中明,等.基于軟閾值和遺傳自適應閾值的車輛制動信號的聯合小波去噪[J].汽車工程,2014,36(6):703～708.

[9] 陳海龍,王長龍,朱紅運.基于磁梯度張量的金屬磁記憶檢測方法[J].儀器儀表學報,2016,37(3):602～609.

[10] Doubov A A.Development of a Metal Magnetic Memory Method[J].Chemical and Petroleum Engineering,2012,47(11):837～839.

[11] 任吉林,林俊明,任文堅,等.金屬磁記憶檢測技術研究現狀與發展前景[J].無損檢測,2012,34(4):3～11.

[12] 陶珂,朱建軍.多指標融合的小波去噪最佳分解尺度選擇方法[J].測繪學報,2012,41(5):749～755.

AnImprovedWaveletThresholdDe-noisingAlgorithmBasedonWeightedAverageMethod

LIU Shu-jun1, LI Sheng-lin1, JIANG Ming1, SONG Zhi-qiang1, BI Jin-you2

(1.PLALogisticsEngineeringUniversity; 2.No.76166TroopofPLA)

Basing on analyzing the principle and characteristics of conventional hard and soft threshold de-nosing algorithms, an improved wavelet threshold de-noising algorithm was proposed, which has weighted average method based and advantages of the classic soft and hard threshold algorithms adopted and the hard threshold’s shortcoming such as the discontinuousness at threshold point overcome to make the reconstruction signal become into smoothness; meanwhile, this algorithm solves the fixed differential existed in the soft threshold meth-

劉書俊(1985-)，講師，從事電磁無損檢測技術的研究，jjxyliushujun@163.com。

TH865

A

1000-3932(2017)03-0239-05

(Continued on Page 318)

2016-05-23，

2016-12-12)