軟件演化環境下基于節點介數的構件重要性度量方法

成 蕾 林 英,2 李 彤

1(云南大學軟件學院 云南 昆明 650091)

王曉芳1 鄭交交1 李 響1

2(云南省軟件工程重點實驗室 云南 昆明 650091)

軟件演化環境下基于節點介數的構件重要性度量方法

成 蕾1林 英1,2李 彤2*

1(云南大學軟件學院 云南 昆明 650091)

王曉芳1鄭交交1李 響1

2(云南省軟件工程重點實驗室 云南 昆明 650091)

在軟件演化中，構件的重要性度量可以為軟件演化的控制和監測提供依據。以軟件體系結構為藍圖和支撐，提出軟件體系結構有向圖模型，引入節點介數對構件的重要性進行度量。并對構件的請求依賴、服務依賴進行分析和研究，通過使用Pearson相關系數進行分析，找出與節點介數最相關的因素。對大量開源軟件源代碼進行實驗，實驗結果表明，用節點介數度量構件的重要性是有效的，并且構件的請求依賴和服務依賴的總和與構件的節點介數最為相關。這也為下一步利用依賴關系衡量構件重要性指明了另一個研究方向。

軟件體系結構 軟件演化 構件 有向圖 節點介數

0 引 言

軟件系統逐漸發展為服務和構件的組合交付，并在社會的發展中出于需要被不斷地調整和擴展，使得軟件系統的規模增大，結構出現了多種層次、不同粒度、多種集成的方式。人們用術語“演化”來描述這種不斷的改變[1,10,13]。這種普遍存在于軟件系統中，軟件系統逐漸變化直至達到理想形態的一系列的復雜變化活動就是軟件演化。

軟件具有構造和演化兩個基本特性[1]。軟件體系結構SA(software architecture)的發展已經趨于成熟，作為藍圖支撐人們從宏觀層面對整體軟件結構進行把握。然而，隨著軟件系統功能和規模的發展，對軟件演化的掌握和控制變得越發復雜，難度也日益增加。傳統的度量方法在軟件演化中有著重要的貢獻，展現了軟件演化的某些特性[2-3,14]。然則，這些傳統度量方法都共性地提早陷入軟件結構中復雜的細節，對于宏觀方面關注不夠，難以整體且全面地把握軟件結構。

20世紀90年代，Bohner[8,11]在提出軟件變化分析過程框架的基礎上使用可達矩陣的概念闡述了軟件變化，但沒有給出組成要素對軟件貢獻大小的概念。Valverde等[13]首先對面向對象的軟件系統進行了研究，他們把系統的類圖抽象為有向網絡圖。Myers[15]和Moura等[16]運用有向網絡來表示軟件系統的結構，在此基礎上提出了基于重構的軟件模型。隨后，國內一批研究人員如汪北陽等[19]使用加權網絡研究復雜軟件系統的軟件網絡，王映輝等[17]、張朝昆等[18]開展軟件結構的研究，獲得了一系列研究成果。

本文的工作主要分為兩個部分，一是基于構件之間的關聯和有向圖的概念，提出SA模型，并引入節點介數作為衡量構件在SA中的重要性指標，通過計算每個構件的節點介數，作為衡量構件重要性的參考；其次為了進一步研究與分析構件之間請求依賴、服務依賴對構件重要性的影響，使用Pearson相關系數分別計算這些依賴關系與節點介數的相關性。通過大量的實驗分析，表明節點介數與構件的總依賴基本一致，依賴關系越強的構件，其節點介數越高，因此節點介數這一指標能夠為軟件演化過程中監控和掌握重要構件提供參考。

1 軟件體系結構的模型

鑒于SA沒有公認的定義，本文采用比較流行的簡單定義[6,9]：SA是組成系統的構件與連接件的高層抽象，構件之間的交互作用關系視為連接件。

構件實現系統中需要的特定功能，符合一套接口標準并實現一組接口。在系統中表現為承擔一定功能的數據或計算單元，也表現為面向軟件體系架構的可復用軟件模塊，是系統中實際存在的可更換部分。

本文不考慮其內部結構，看做一個不透明的整體。把一個軟件系統實例視作一個SA時，SA中構件之間的交互和依賴是有方向性的，構件之間的交互是無權有向的，則可以將SA的模型定義如下：

定義1SA的模型。將一個軟件系統實例的SA的模型G描述為一個無權有向圖三元組：

(1)NG是軟件系統實例的SA模型的名稱；

(2)V(G)是構成軟件系統的構件所代表的節點的集合；

(3)E(G)是構成軟件系統的構件間關系代表的無權有向邊的集合。

定義2構件。一個節點所代表的構件V的描述是一個二元組：

(1)NC是構件的名稱；

(2)FC是構件的功能描述。

定義3構件間關聯。將構件間的交互關系作為無權有向邊E描述為一個三元組：

(1)En是有向邊的唯一標識；

(2)Vi是發起依賴的構件，即起始節點；

(3)Vj是接受依賴的構件，即終止節點；

(4) 即表示節點Vi指向節點Vj。

定義4構件的請求依賴。在SA的模型G=中，構件vi∈V(G)，以構件vi作為起始節點的邊的總數稱作構件vi的請求依賴，記為dreq(vi)。

構件的請求依賴描述了構件依賴其他模塊的程度和關系。構件的請求依賴越高，則表示該構件直接依賴的構件數量越多，該構件的行為也就越復雜，所在的構件層次也就越高。

定義5構件的服務依賴。在SA的模型G=中，構件vi∈V(G)，以構件vi作為終止節點的邊的總數稱作構件vi的服務依賴，記為dser(vi)。

構件的服務依賴刻畫了構件在SA中被其他模塊直接依賴的程度。構件的服務依賴越高，構件的直接被依賴性越強，在SA中的復用率也就越高，說明該構件的行為功能越固定。

構件的請求依賴與構件的服務依賴的總和，稱為構件的總依賴，記作dsum(vi)。

定義6節點介數。給定圖G=，節點vi∈V(G)，在圖G中經過節點vi的最短路徑總數目與圖G中所有的最短路徑之比稱為vi的節點介數，記為C(vi)。則：

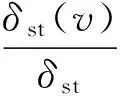
(1)

其中：δst是節點s到節點t的所有最短路徑的總數目，δst(v)是節點s到節點t的最短路徑數中經過節點v的最短路徑數目。

節點介數是一個重要的全局幾何量，反應了節點在整個圖中的作用和影響力。將SA的模型抽象為有向圖模型后，在SA演化中引入節點介數，可以直觀地觀察到構件對應的節點在整個SA中的地位和影響力。節點介數是衡量構件在SA演化時的關鍵程度和地位的重要指標，對掌握和控制構件演化前后的影響范圍和強度有著直觀的指導作用和很強的現實意義。

在本文的實驗中，將類擬為構件，類關系擬為SA的模型中的無權有向邊，其對應關系如表1。

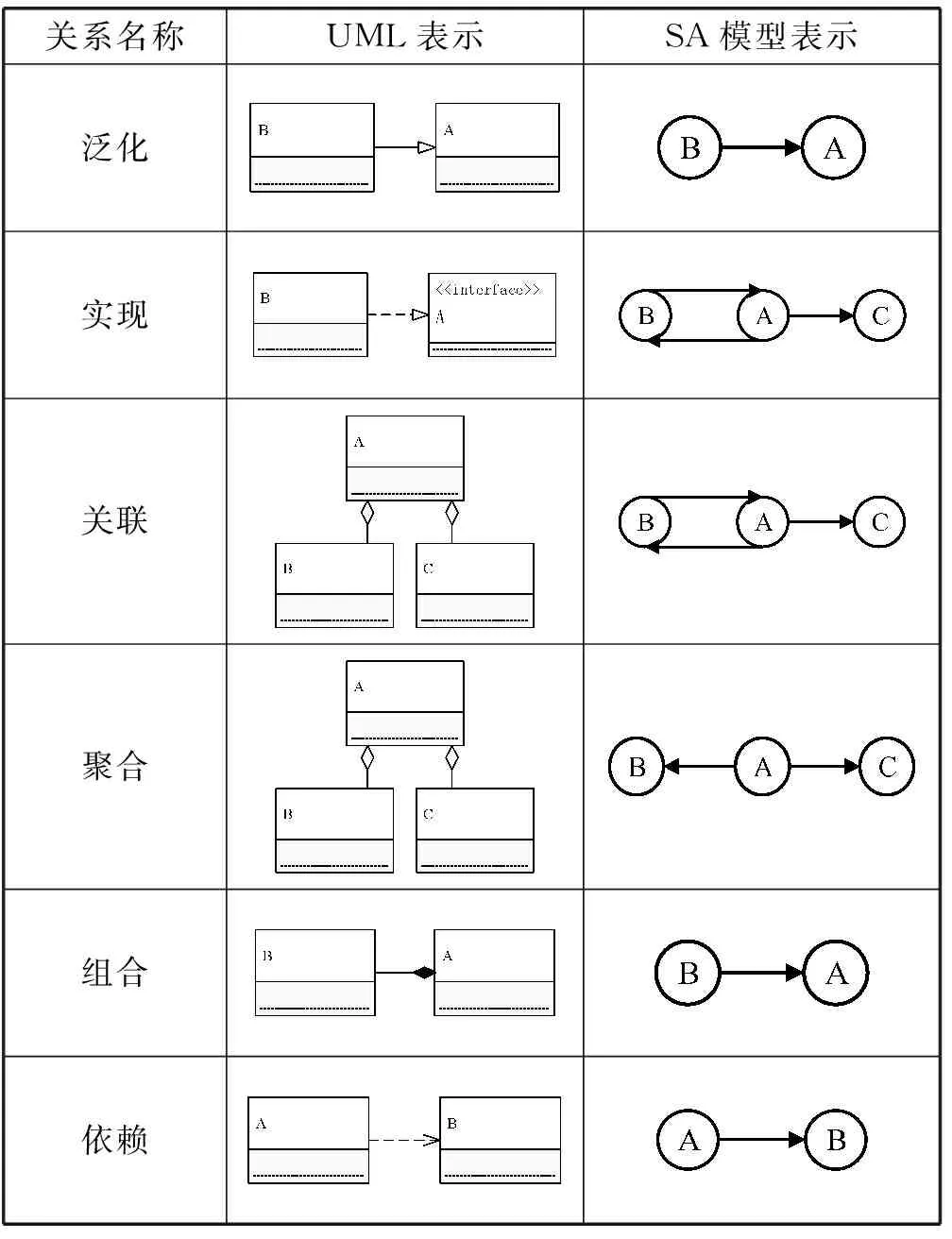
表1 SA的模型關系

2 演化環境下的構件重要性度量

演化是所有軟件系統都必經的活動，系統的整體結構趨于復雜、構件數量龐大，尋找出結構中的重要構件。為軟件演化的檢測和可控提供依據的同時，也是掌握和評價演化的一個重要方面，對軟件的演化工作顯得尤為重要。

2.1 構件重要性度量方法

對構件的重要性進行度量，主要有5個步驟，包括：

(1) 獲取構件和構件間關聯。將源代碼中的類作為一個構件，通過掃描源代碼，得到構件名稱標識和構件之間的關系。

(2) 將構件和構件之間的關系數據進行處理，并映射為鄰接矩陣。若構件的個數為n，將構件之間的關系映射為n維的鄰接矩陣M，并默認M11，M22，…，Mnn的值為0，有特殊自調用的構件除外；例如，若構件1對構件2有依賴關系，構件2對構件1沒有依賴關系，則M12的值為1，M21的值為0。

(3) 以鄰接矩陣M為基礎，計算出每個節點的構件請求依賴、構件服務依賴和構件的總依賴。

(4) 計算每個節點的節點介數。計算全圖的最短路徑，得到全圖的最短路徑總數目以及各個節點的經過該節點的最短路徑數目后，根據式(1)計算每個構件的節點介數。根據節點介數的大小度量出在SA中的重要構件。

(5) 分別計算構件的請求依賴、構件的服務依賴、構件的總依賴與節點介數的Pearson相關系數。根據式(2)分別進行計算，并研究與分析和節點介數最相關的因素。

在本文中使用的Pearson相關系數的計算公式為：

(2)

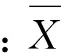
在Pearson相關系數的定義中：相關系數絕對值在[0.8,1.0]，是極強相關；相關系數絕對值在[0.6,0.8]，是強相關；相關系數絕對值在[0.4,0.6]，是中等程度相關；相關系數絕對值在[0.2,0.4]，是弱相關；絕對值在[0,0.2]，是極弱相關或無相關。

使用Pearson相關系數來計算節點構件的請求依賴、構件的服務依賴、構件的總依賴和節點介數的相關性。在實驗中，節點介數、構件的請求依賴、構件的服務依賴、構件的總依賴之間，兩個變量的觀測值是成對的，每對觀測值之間相互獨立，且他們的標準差均不為0，那么Pearson相關系數就是有定義的。

2.2 算 法

算法1獲取SA模型的鄰接矩陣算法。

輸入：構件名稱標識鏈表Name和構件間交互關系鏈表Connection。

輸出：SA的模型的鄰接矩陣Matrix。

初始化：二維數組Matrix用于存儲SA模型的鄰接矩陣，Matrix的行列長度均等同于鏈表Name的長度。

Begin

For i ← 0 to length[Connection] do

row ← get index of component name 1 from Connection[i] in Name

column ← get index of component name 2 from Connection[i] in Name

Matirx[row][column] = 1

EndFor

End

例如在實驗一中用Eclipse 3.0獲得的部分矩陣如下：

得到SA模型的鄰接矩陣之后便可以計算出每個構件的請求依賴和服務依賴。在計算構件的請求依賴時，Matrix[i][]這一列中有多少個1，最后累積相加所得的結果便是節點vi所對應的構件的請求依賴；同樣地，在計算構件的服務依賴時，Matrix[][j]這一行中有多少個1，最后累積相加所得的結果便是節點vj所對應的構件的服務依賴。每個構件的請求依賴和服務依賴相加就得到節點的總依賴。

算法2SA有向圖模型的全圖最短路徑算法。

輸入：SA模型的鄰接矩陣Matrix。

輸出：SA模型的全圖最短路徑Pathes。

初始化：鏈表Pathes用于存儲圖中所有的最短路徑。

Begin

For i ← 1 to length[Matrix] do

For j ← 1 to length[Matrix[i]] do

shortest(i,j) = minWeight(i,j)

EndFor

EndFor

For k ← 1 to length[Matrix] do

For i ← 1 to length[Matrix] do

For j ← 1 to length[Matrix] do

If (shortest(i,k)+shortest(k,j) < shortest(i,j)) Then

shortest(i,j) = shortest(i,k)+shortest(k,j)

EndIf

EndFor

EndFor

EndFor

End

算法3SA模型的節點介數計算算法。

輸入：SA模型的全圖最短路徑Pathes，構件名稱標識鏈表Name。

輸出：SA模型的各個構件的節點介數。

初始化：鏈表Betweenness用于存儲SA模型的節點介數，鏈表Betweenness的長度等同于構件名稱標識鏈表Name的長度。

Begin

For i ← 0 to length[Name] do

k = 0

For j ← 0 to length[Pathes] do

If Name[i] exists in Pathes[j]

k ← k + 1

Else continue

EndIf

EndFor

Betweenness[i] = k/length[Pathes]

EndFor

End

3 實驗分析

本文選取的開源軟件近一百種，包括各種功能，例如軟件開發平臺、編程語言源代碼包、開源專業性軟件等，可按照節點的數量分為三類：節點數小于50的小規模軟件，節點數在50至200的中規模軟件，節點數大于200的大規模軟件。

結果發現，本文的方法是切實有效的，且與軟件的規模和功能種類無關，其構件的總依賴和節點介數的走向趨勢總是相符的。但是節點介數的體現與軟件的結構設計有關，在那些擁有良好設計、體系結構的軟件中，所得實驗結果最為理想，不僅其構件的總依賴和節點介數的變化總是趨于同步，而且構件之間的節點介數的區別更加明顯；反之，沒有良好的體系結構支撐的軟件系統中，構件之間的節點介數幾近一致，導致構件之間的度量困難。

由于篇幅的限制，最后選取屬于大規模軟件的Eclipse 3.0和屬于中規模的Jabref的源碼作為典型的兩個實驗示例進行分析。

3.1 實驗一

使用Eclipse 3.0的源代碼作為實驗數據。

圖1為Eclipse 3.0的構件的請求依賴、構件的服務依賴的分布曲線和構件的總依賴、節點介數的百分比折線圖。由于節點介數的取值在[-1,1]之間，范圍變化小，而總依賴的值遠大于節點介數的值，為了更清楚地看到總依賴和節點介數的關系和走向趨勢，采用百分比折線圖進行分析。在圖中Y軸表示了構件的請求依賴、構件的服務依賴的大小，X軸代表節點。

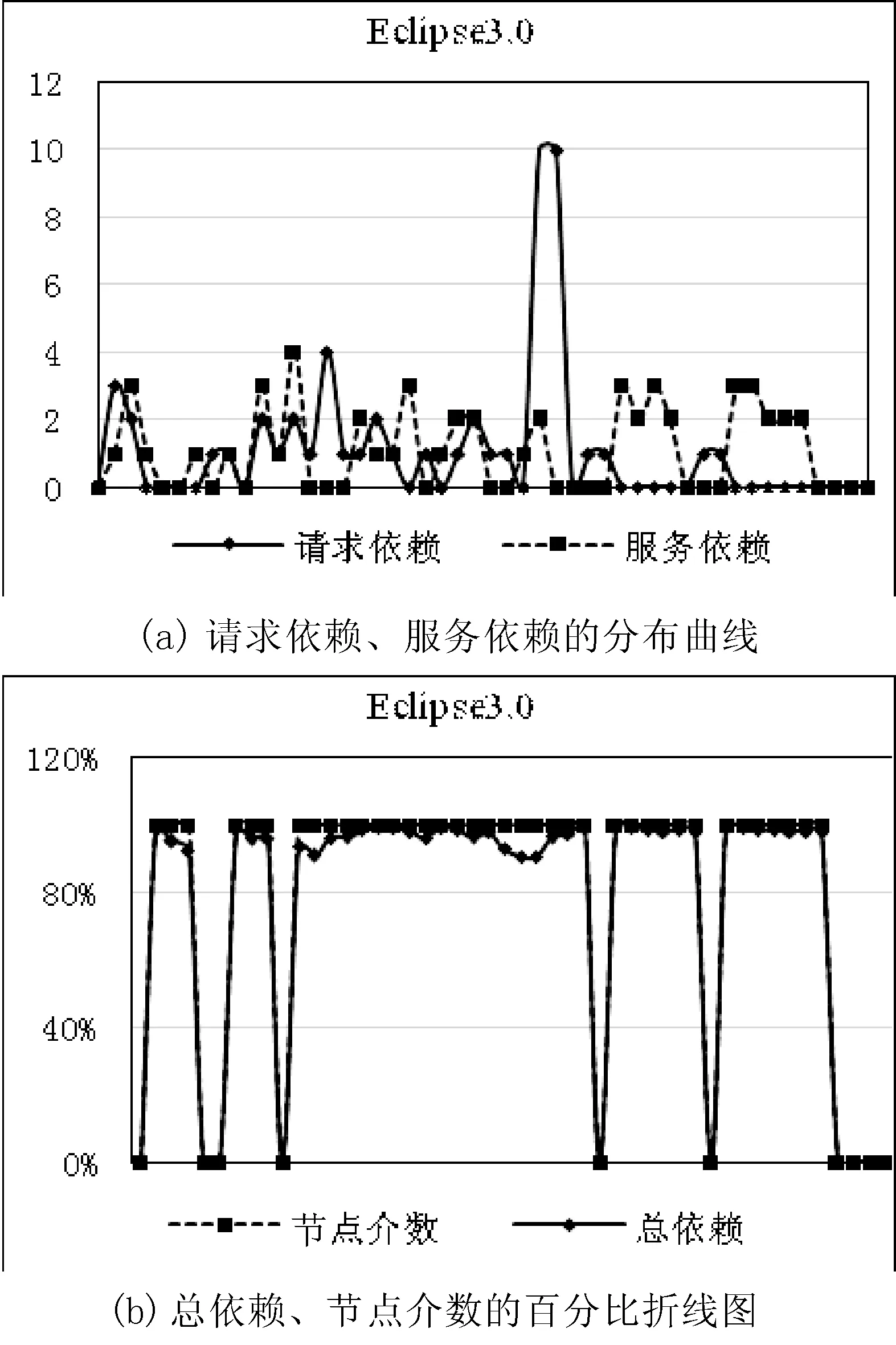
圖1 Eclipse 3.0的分布折線圖

通過觀察折線圖的走向，不難發現構件的請求依賴和構件的服務依賴之間是沒有明顯的相關關系，即構件的請求依賴和構件的服務依賴之間沒有呈現規律的對應關系，請求依賴高的構件可能服務依賴高也可能服務依賴低。而構件的總依賴和節點介數的起伏走向基本是一致的，意味著總依賴高的構件節點介數也高。構件的節點介數越高，構件在軟件體系結構中的功能、位置也就越重要。

采用式(2)計算度和節點介數的相關性，用Pearson相關系數來判斷度和節點介數之間是否存在如折線圖所呈現出的相關關系。表2為Eclipse 3.0相關性分析。

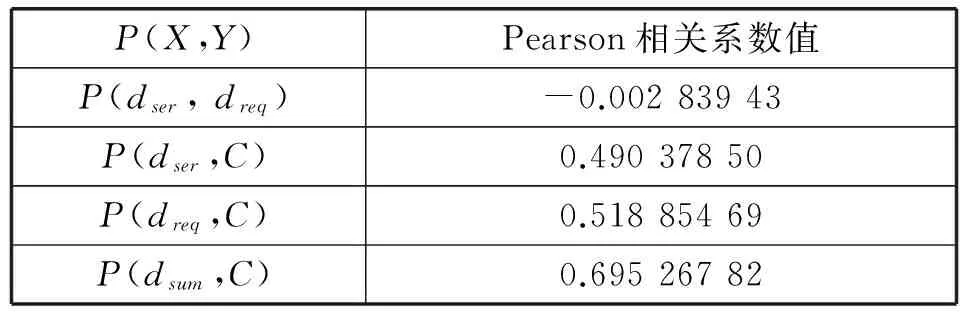
表2 Eclipse3.0相關性分析

由Pearson相關系數值的計算結果可以看出，折線圖所展示出的趨勢是正確的。構件的總依賴與節點介數為強正相關，構件的總依賴越大節點介數也越大，構件的服務依賴和請求依賴分別與節點介數為中等程度正相關，而請求依賴與服務依賴之間是極弱負相關或無相關。

3.2 實驗二

使用Jabref的源代碼作為實驗數據。

圖2為Jabref的構件的請求依賴、構件的服務依賴的分布曲線和構件的總依賴、節點介數的百分比折線圖。Y軸表示了構件的請求依賴和構件的服務依賴的大小，X軸代表節點。

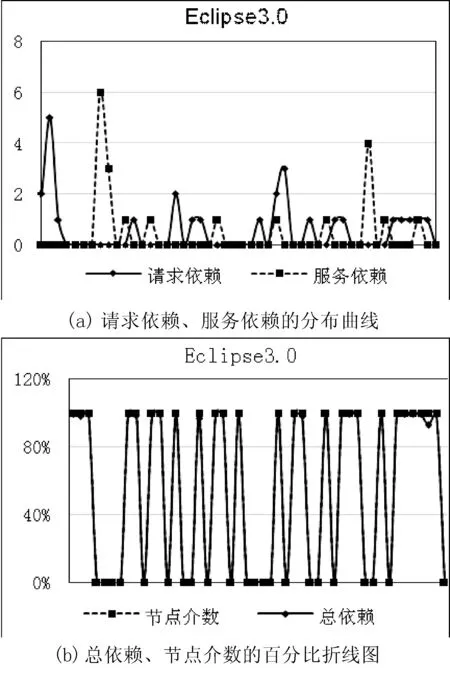
圖2 Jabref的分布折線圖

在Jabref的折線圖中，構件的請求依賴和服務依賴沒有呈現規律的相關趨勢，而構件的總依賴和節點介數的起伏幾乎重疊，這表明，在Jabref中，總依賴高的構件其節點介數也高。

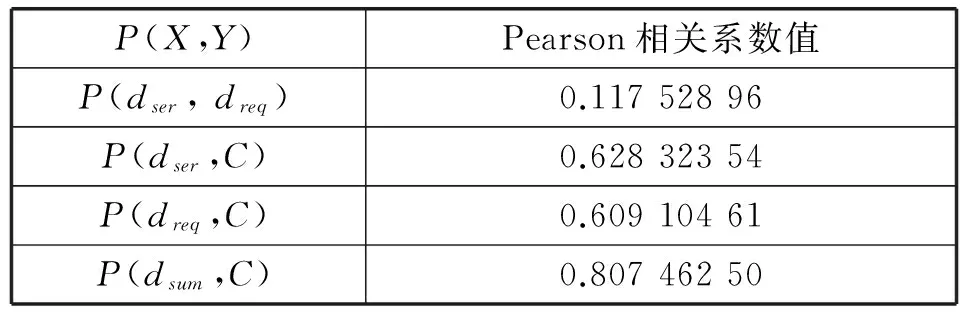
表3 Jabref相關性分析

Jabref的相關性分析再次證明折線圖展示的相關趨勢是正確的。構件的請求依賴和服務依賴之間是極弱正相關或不相關，構件的請求依賴、服務依賴分別與節點介數強正相關，總依賴與節點介數極強正相關，節點介數隨總依賴的增大而增大。

通過計算Eclipse 3.0和Jabref的構件的服務依賴和請求依賴的Pearson相關系數，可見構件的服務依賴和請求依賴的分布是沒有規律的，它們之間不存在相關性。

根據Pearson相關系數分析可知，在軟件體系結構中，構件的總依賴和節點介數均呈現極強正相關，而構件的服務依賴與節點介數的Pearson相關系數和構件的請求依賴與節點介數的Pearson相關系數的趨勢變化并不穩定。由節點介數的定義可知，一個構件的節點介數與該構件的服務依賴、請求依賴和總依賴有著直接的關系，當一個構件的總依賴越大，那么這個構件在整個軟件體系結構中的地位和重要程度也就越高，相應的節點介數越高；反之，若一個構件的總依賴越低，甚至沒有，那么這個構件在整個軟件體系結構中的地位和重要程度越低，節點介數也就越低。

構件的總依賴與其變化最密切相關，通過節點介數來判斷構件在整個軟件體系結構中的地位和重要程度的時候，構件的總依賴也是一個關鍵的判斷因素。

4 結 語

實驗證明使用節點介數度量軟件演化環境下的構件的重要性，是有效的，補充了傳統的度量方法在掌握軟件體系結構宏觀特性方面的不足。

在整個軟件體系結構中，構件的請求依賴高的節點往往獨立性較差，對底層構件或其他基礎構件的依賴較強，耦合度高，功能比較復雜；構件的服務依賴高的節點通常內聚度高，結構穩定并且功能單一。

通過對構件的總依賴和節點介數的計算，可以清晰地度量構件在整個軟件體系結構中的重要性。在軟件體系結構演化的時候，可以更好地把握這些重要的節點的演化過程，降低演化風險，有助于監控管理那些在演化活動中比較難控制的活動和構件。軟件體系結構中構件的請求依賴和服務依賴沒有規律的相關關系，而構件的總依賴和節點介數之間通常表現為強正相關或極強正相關，即總依賴高的構件節點介數也高。

總依賴與節點介數極強正相關，為構件的重要性度量指明了另一個研究方向，尤其是在一個龐大的軟件體系結構中時，如何在計算時對源代碼中數量眾多的節點進行降維，從而更加快速地計算構件的總依賴是下一步的研究重點。

[1] Bianchi A,Caivano D,Marengo V,et al.Iterative reengineering of legacy systems[J].IEEE Transactions on Software Engineering,2003,29(3):225-241.

[2] Zeng J,Sun H L,Liu X D,et al.Dynamic Evolution Mechanism for Trustworthy Software Based on Service Composition[J].Journal of Software,2010,21(2):261-276.

[3] Song W,Ma X X,Lu J.Instance migration in dynamic evolution of web service compositions[J].Chinese Journal of Computers,2009,32(9):1816-1831.

[4] Huang G,Mei H,Yang F Q.Runtime recovery and manipulation of software architecture of component-based systems[J].Automated Software Engineering,2006,13(2):257-281.

[5] Wilfredo T.Software Fault Tolerance:A Tutorial[J].Pomales,2000,1(2):220-232.

[6] Liu Y,Zhang S K,Wang L F,et al.Component-Based Software Frameworks and Role Extension Form[J].Journal of Software,2003,14(8).

[7] Brunet J,Murphy G C,Serey D,et al.Five Years of Software Architecture Checking:A Case Study of Eclipse[J].IEEE Software,2015,32(5):1-1.

[8] Bohner S A.Impact analysis in the software change process:a year 2000 perspective[C]//International Conference on Software Maintenance.IEEE Computer Society,1996:42-51.

[9] Shaw M,Garlan D.Software architecture:perspectives on an emerging discipline[J].Prentice Hall,2010,24(1):129-132.

[10] Ambriola V,Tortora G.Advances in Software Engineering and Knowledge Engineering[M].World Scientific,1993.

[11] Bohner S A.Software change impacts-an evolving perspective[C]//International Conference on Software Maintenance.IEEE Computer Society,2002:263.

[12] Drange P G,Dregi M,Hof P V.On the Computational Complexity of Vertex Integrity and Component Order Connectivity[J].Algorithmica,2014,8889:285-297.

[13] Valverde S,Cancho R F I,Sole R V.Scale-free Networks from Optimal Design[J].Europhysics Letters,2002,60(4):512-517.

[14] Eiben A E,Smith J.From evolutionary computation to the evolution of things[J].Nature,2015,521(7553):476-482.

[15] Myers C R.Software systems as complex networks:structure,function,and evolvability of software collaboration graphs[J].Physical Review E,2003,68(4 Pt 2):352-375.

[16] de Moura A P,Lai Y C,Motter A E.Signatures of small-world and scale-free properties in large computer programs[J].Physical Review E Statistical Nonlinear & Soft Matter Physics,2003,68(2):017102.

[17] 王映輝,王立福.軟件體系結構演化模型[J].電子學報,2005,33(8):1381-1386.

[18] 張朝昆,崔勇,唐翯祎,等.軟件定義網絡(SDN)研究進展[J].軟件學報,2015,26(1):62-81.

[19] 汪北陽,呂金虎.復雜軟件系統的軟件網絡結點影響分析[J].軟件學報,2013,24(12):2814-2829.

AMETHODOFCOMPONENTIMPORTANCEMEASUREMENTBASEDONNODEBETWEENNESSINSOFTWAREEVOLUTIONENVIRONMENT

Cheng Lei1Lin Ying1,2Li Tong2*Wang Xiaofang1Zheng Jiaojiao1Li Xiang1

1(CollegeofSoftware,YunnanUniversity,Kunming650091,Yunnan,China)2(KeyLaboratoryforSoftwareEngineeringofYunnanProvince,Kunming650091,Yunnan,China)

In software evolution, the importance measure of components can provide the basis for the control and monitoring of software evolution. With software architecture as blueprint and support, this paper proposes a software architecture directed graph model, and introduces node betweenness to measure the importance of components. And the component request dependence and service dependence are analyzed and studied. By using the Pearson correlation coefficient analysis, the factors which are most related to the node betweenness are found out. Through the experiment of a large number of open source software source code, the experimental results show that it is effective to use node betweenness to measure the importance of component, and the sum of component request dependence and the component service dependence is the most correlative factor to betweenness. This also points to another research direction for measuring the importance of components by using dependencies.

Software architecture Software evolution Component Directed graph Node betweenness

TP311

A

10.3969/j.issn.1000-386x.2017.10.005

2016-12-12。國家自然科學基金項目(61379032)。成蕾，碩士，主研領域：軟件工程理論與方法。林英，副教授。李彤，教授。王曉芳，碩士。鄭交交，碩士。李響，碩士。