多重網格法二維Helmholtz方程解算及其在電磁法正演模擬中的應用

楊振威 馮 磊 趙 寧 趙秋芳 楊雙安

（①河南理工大學資源環境學院，河南焦作454000；②中原經濟區煤層（頁巖）氣河南省協同創新中心，河南焦作454000；③河南理工大學計算機學院，河南焦作454000）

·非地震·

多重網格法二維Helmholtz方程解算及其在電磁法正演模擬中的應用

楊振威①②馮 磊①②趙 寧*③趙秋芳①②楊雙安①②

（①河南理工大學資源環境學院，河南焦作454000；②中原經濟區煤層（頁巖）氣河南省協同創新中心，河南焦作454000；③河南理工大學計算機學院，河南焦作454000）

為了提高Helmholtz方程數值計算效率和精度，研究了多重網格算法，并對比研究了該算法與共軛梯度法、預處理共軛梯度法和超松弛法求解二維Helmholtz方程的計算精度和收斂速度，網格剖分采用可實現網格自動細化的Delaunay三角網格算法。研究結果表明：多重網格法在計算時間和迭代收斂效率方面具有較大優勢，但其迭代計算誤差大于其他算法，這或許與不規則網格剖分導致網格層間插值、限制算子擴大了計算誤差有關。最后，初步研究了基于多重網格算法的大地電磁二維正演模擬響應。

多重網格 Helmholtz方程 大地電磁 共軛梯度

1 引言

大地電磁三維正、反演是計算地球物理研究的熱點和難點，其面臨的一個重要問題是計算量大、效率低，且數值解的精度不高。大地電磁正演模擬基于Helmholtz方程，開展快速求解Helmholtz方程的數值算法研究，對于提高正、反演計算速度具有重要的意義［1-3］；多重網格法（MG）在不同尺度的網格層上迭代求解線性方程組，具有收斂速度快、計算效率高的特點，對于計算地球物理正演問題具有一定的研究價值［4-7］。

Mulder［8］采用多重網格算法研究了時諧電磁場的擴散規律；Plaks等［9］研究了多重網格算法在地球物理研究中的開邊界問題；Zaslavsky等［10］應用自適應多重網格技術進行分子生物學模擬；Tang等［11］研究了基于自適應多重網格有限元法的三維直流電正演模擬，證明該算法相對于解析解的誤差小于1%；柳建新等［12］和 Mitsuhata等［13］應用廣義傅里葉譜分析了基于多重網格算法的一維大地電磁正演計算的收斂性。

上述研究在MG法及其計算地球物理領域的應用取得了一定成果，但也存在不足之處，即未詳盡地研究MG法的計算效率及收斂性。本文在研究了多重網格法求解二維Helmholtz方程的迭代次數、運算時間和誤差的基礎上，初步研究了該算法在大地電磁測深正演模擬中的應用。

2 多重網格算法

MG法可以分為代數多重網格法和幾何多重網格法。多重網格法源自迭代求解線性方程時，誤差分量的傅里葉分量可以分為頻率高、變化快的高頻分量和頻率低、變化慢的光滑分量，而高頻分量和光滑分量是相對于網格尺度而言的，在不同尺度的網格層上迭代求解方程，將在細網格層上平滑后的誤差準確地投射到粗網格層上，可以達到快速收斂的效果，從而減小計算量，提高計算效率。近年來，該方法在流體力學、結構力學等涉及大型稀疏矩陣計算的領域得到廣泛應用［14-17］。

MG法的迭代計算包含以下過程：

①預處理，在細網格D h上進行若干次松弛迭代，即A hu h=f h；

②殘差估計，rh=f h-A hu h；

④粗網格方程求解，

⑥循環迭代，直至最大迭代次數或達到誤差限。

上述計算過程中，D為求解區域，h為細網格層的網格尺寸，A為系數矩陣，A h為細網格層系數矩陣，f h為細網格層上矩陣方程的右端項，R為從粗網格層至細網格層的限制算子，I為從細網格層至粗網格層的插值算子。

圖1a為多重網格迭代過程示意圖，G代表松馳迭代算法，N代表迭代次數，一般N=3～5，H代表最粗網格層網格尺寸，uih、G ih、eih和f ih（i=0，1，2，…）分別是定義在第ih網格層上的迭代解、迭代矩陣、迭代誤差和右端項。經過若干次迭代，獲得滿足精度要求的迭代近似解。圖1b是層間網格解及誤差傳遞示意圖，圖中紅黑圓點表示細網格層的迭代解，紅黑圓圈表示粗網格層上的迭代解，該解可由細網格解插值生成。

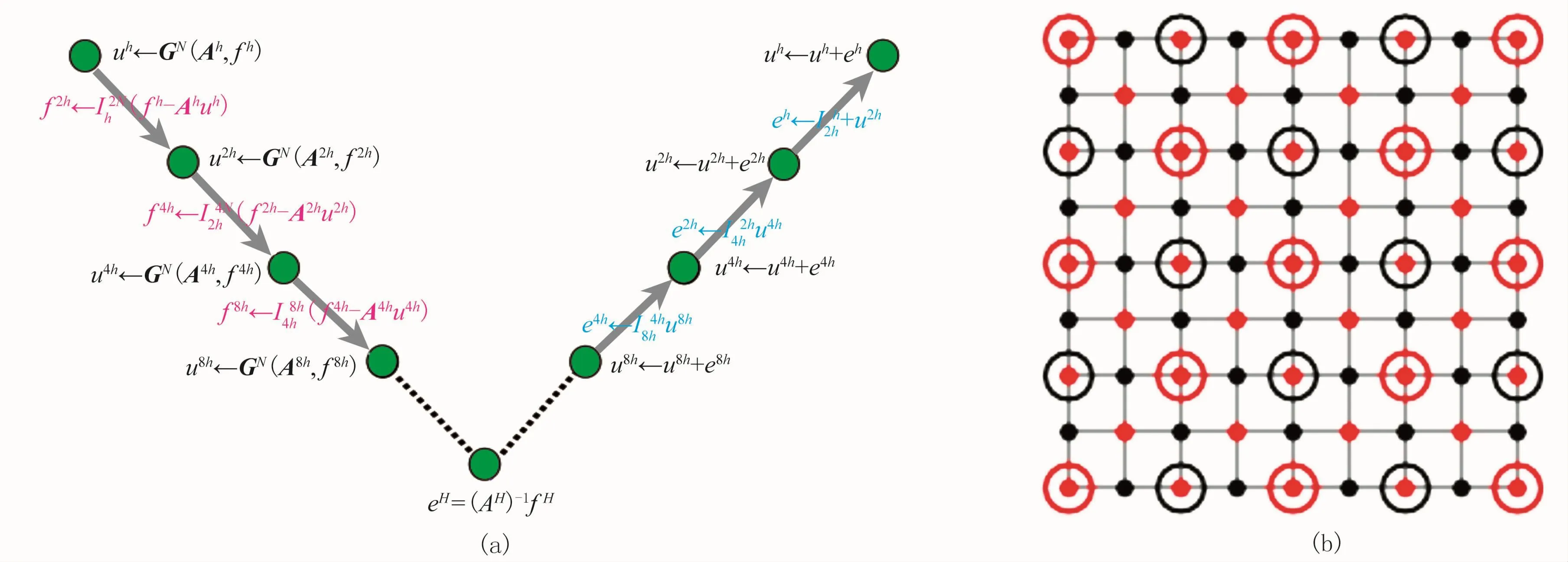
圖1 MG法迭代計算示意圖

網格剖分采用Delaunay三角剖分算法，初次網格剖分后再進行5次左右的網格自動加密處理（如圖2所示），進而提高解的精度，但同時計算量和計算時間呈指數級增長。

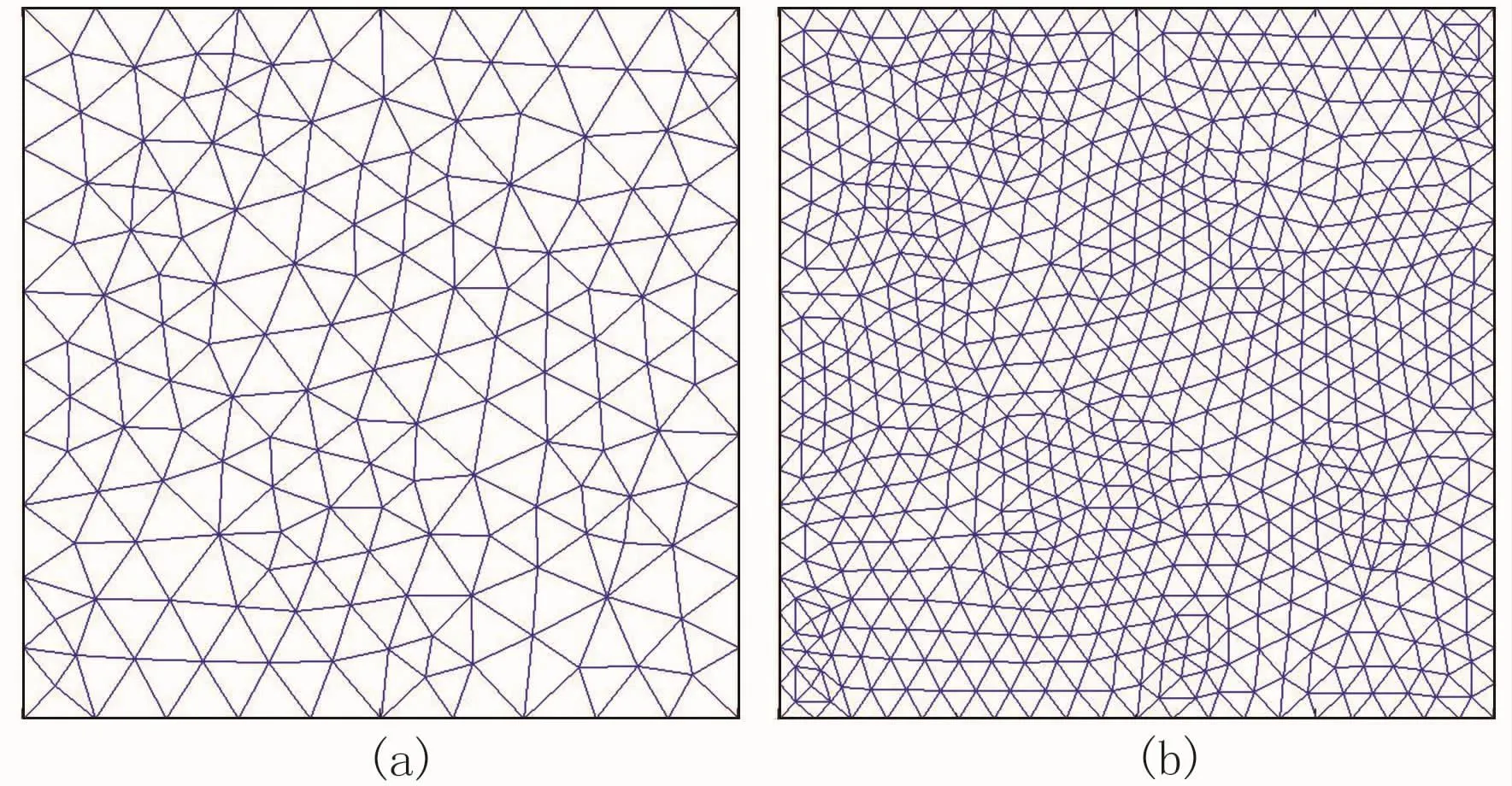
圖2 Delaunay三角網格剖分示意圖

3 二維Helmholtz方程的多重網格法

在研究區域D及邊界?D上的二維Helmholtz方程邊值問題

上述邊值問題與下列變分問題等價

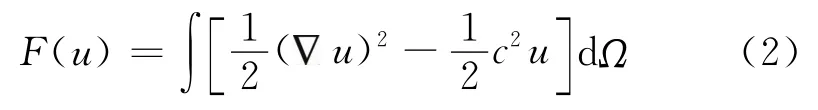
式中：F（u）表示u的泛函；c為未知系數。

網格剖分是進行有限元解算的關鍵步驟，網格剖分密度和質量對有限元法計算精度、計算效率和收斂性起著十分重要的作用。本次網格剖分基于Delaunay三角剖分算法［13］，為了提高解的精度，在7個網格層上迭代求解，網格數量逐層倍增，最底層網格數量約2萬個。

在區域D上對Helmholtz方程三角網格離散化，c2=0.3，D=［-1，1］2，分別采用 MG法、共軛梯度法（CG）、預處理共軛梯度法（PCG）及超松弛法（SOR）求解離散化后的有限元線性方程組AU=f，U表示方程組的解，f表示右端項。

數值計算采用Matlab軟件編程并在PC機（CPU2.2GHz，內存2GB）雙精度型下進行，在 MG法計算過程中，采用不規則三角網格V循環、七層網格套迭代。當最精細網格層上的誤差殘量的L2范數小于控制收斂準則ε（ε取1.0×10-4）時，計算即為收斂。圖3為基于MG法和SOR法的二維Helmholtz方程解的曲面圖。

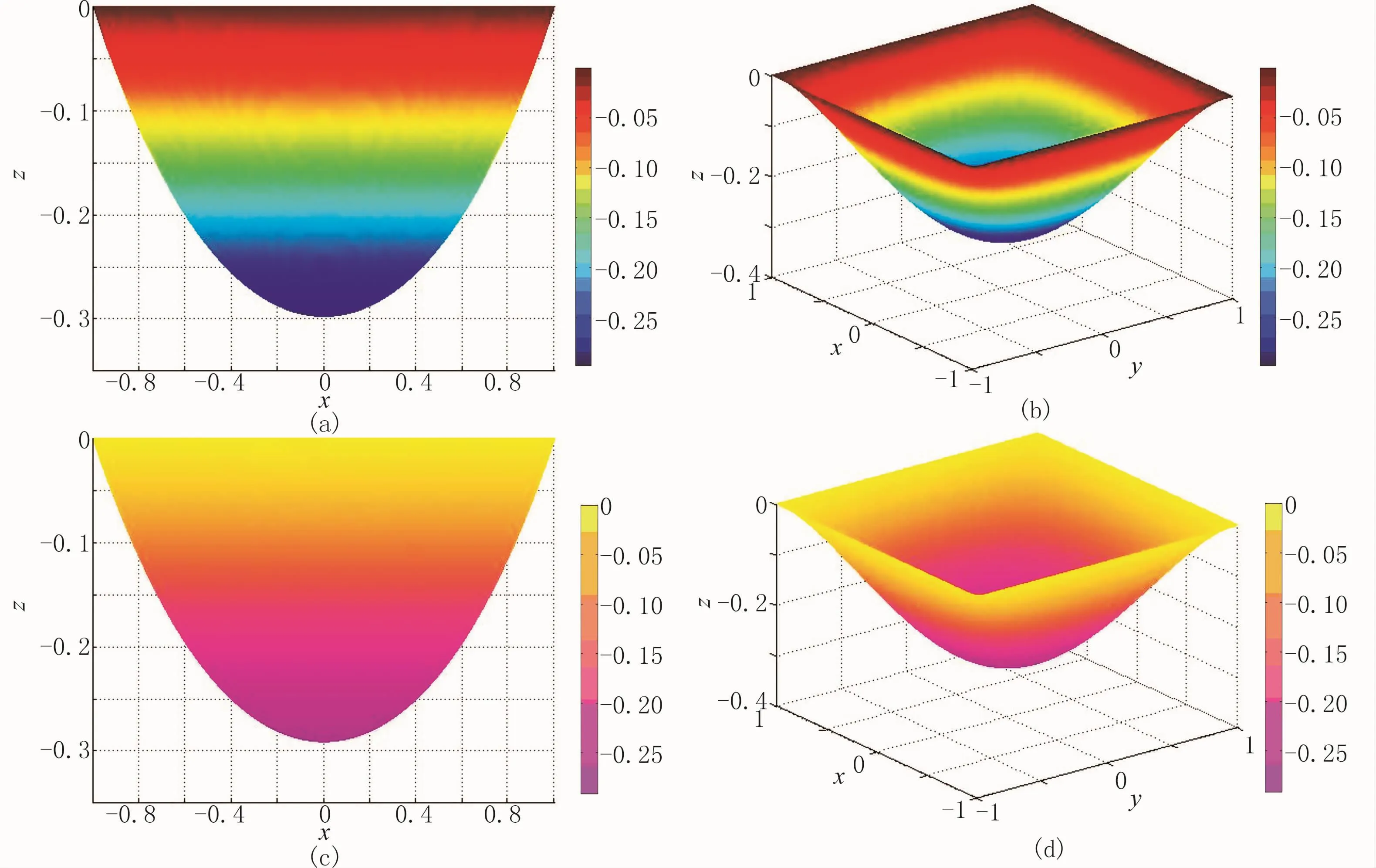
圖3 Helmholtz方程解曲面圖

4 計算結果分析

4.1 誤差分析

為了估計多重網格法的計算精度，采用歐幾里得范數對迭代解進行誤差分析。誤差分析公式如下

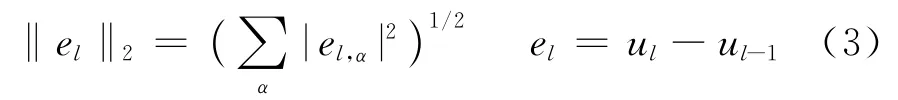
式中：el為第l次迭代后的相對誤差，即本次迭代近似解與上次迭代近似解的歐氏范數；α為網格節點序號。

為了深入分析MG法的計算精度和收斂性，對比研究了該算法與CG法、PCG法、SOR法的相對誤差，見表1。由表可知，無論網格單元個數多與少，該算法在計算精度方面均不具有優勢，或者說其計算誤差大于其他三種算法，這或許與其在多個網格層進行不規則三角網格剖分有關，具體原因有待進一步研究。

4.2 收斂性分析

圖4是網格數分別為11425和45377個時，MG和PCG法迭代的收斂曲線。從圖中不難看出，MG法的收斂速度明顯優于PCG法，說明MG法的收斂速度與網格尺度無關，且初始收斂速度明顯快于PCG法。隨著迭代次數的增加，誤差減小，這兩種算法的收斂速度差距逐步縮小。

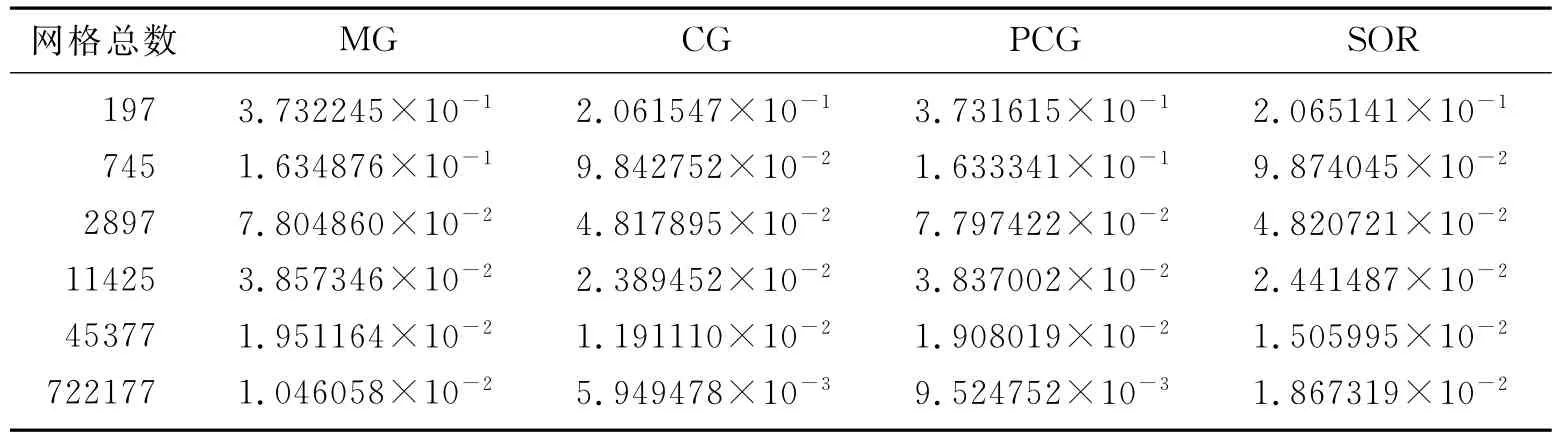
表1 不同方法計算相對誤差對比

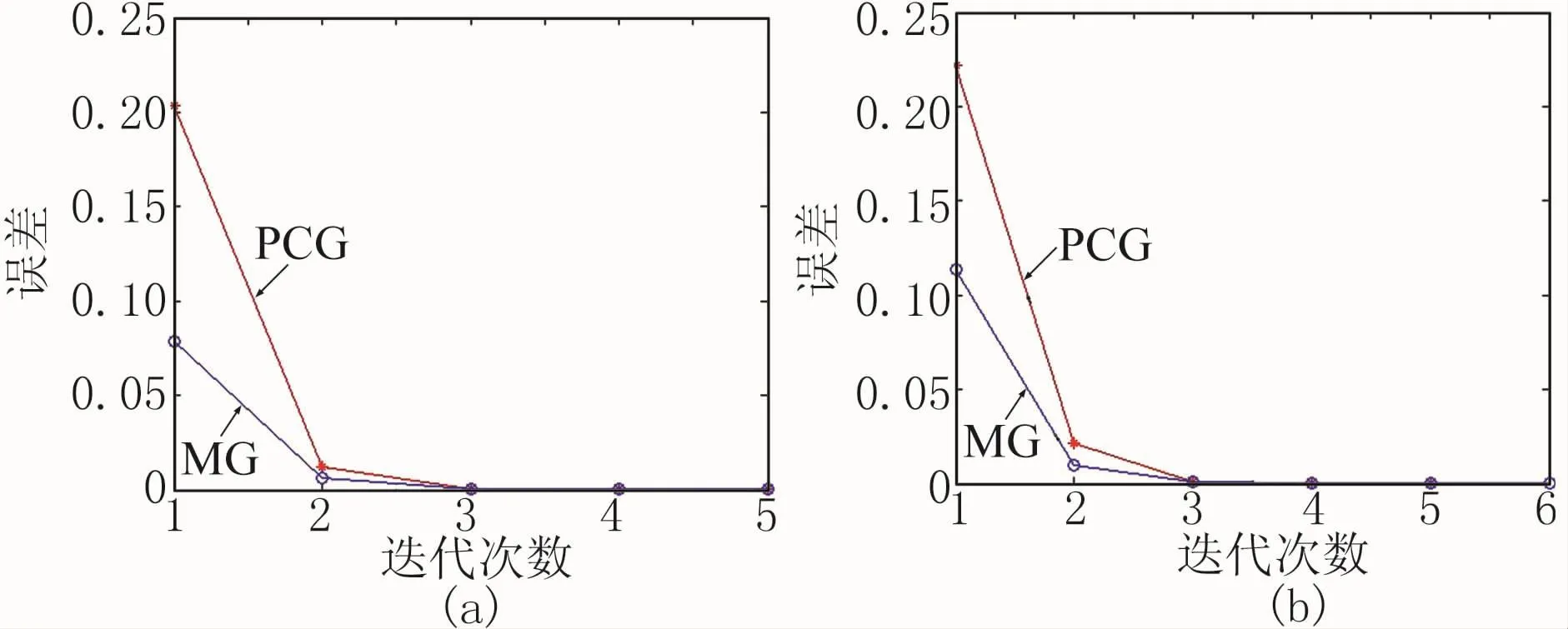
圖4 MG法（a）和PCG法（b）收斂曲線對比圖

4.3 計算時間分析

計算時間是衡量算法計算效率的重要參考指標。在設置相同誤差精度的條件下，采用Matlab中計算程序運行時間的函數（tic／toc），分別得到 MG法、CG法、SOR法和PCG法的計算時間如表2所示。從表中可以看出，當網格單元個數較少時，MG法在計算時間上優勢并不明顯；當網格個數較多時（如722177），MG法的計算時間分別是SOR法的近1／10、CG法的約1／2、PCG法的約1／6，具有明顯優勢。

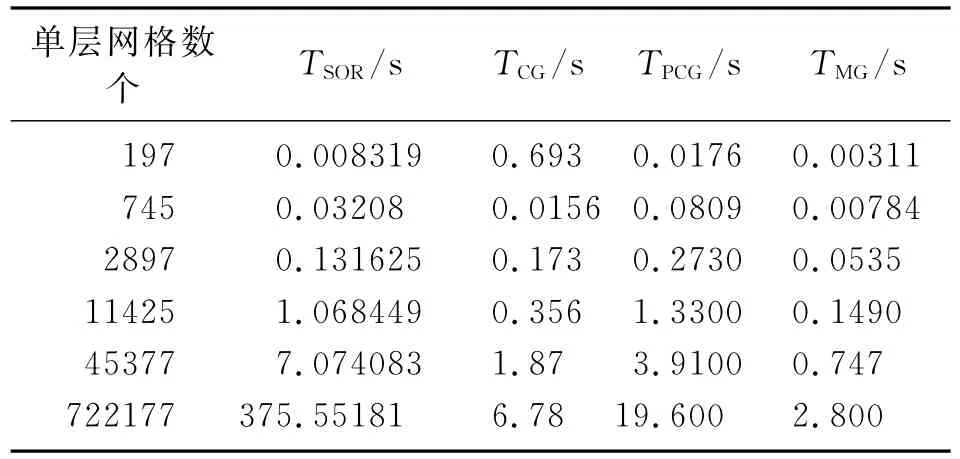
表2 不同算法計算時間對比

5 基于多重網格法的大地電磁二維正演模擬

5.1 邊值問題

為了檢驗MG法在大地電磁二維正演模擬中的計算特性，初步研究了均勻半空間條件下二維地電模型的大地電磁正演響應。大地電磁測深法二維邊值問題可以表示為

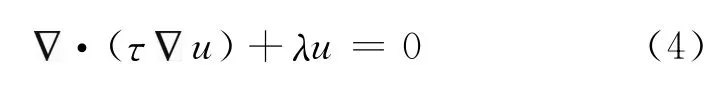
對于上邊界，u=1；對于側邊界，對于底邊界，

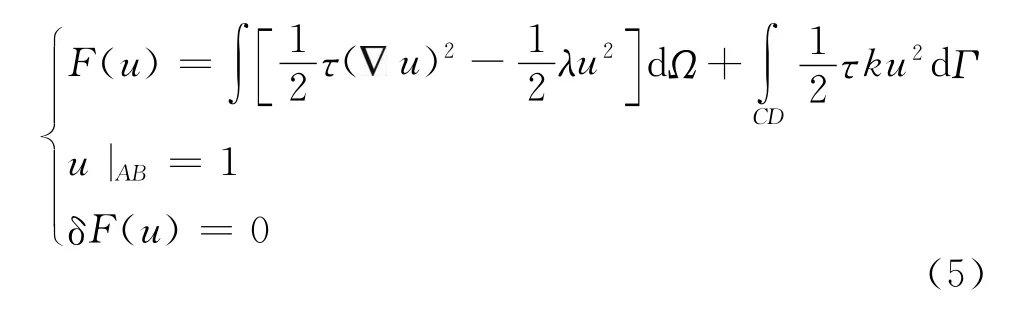
5.2 限制算子

MG法的關鍵是殘量和近似解在網格層間進行精確傳遞，即合理設計粗—細網格層間插值和限制算子。

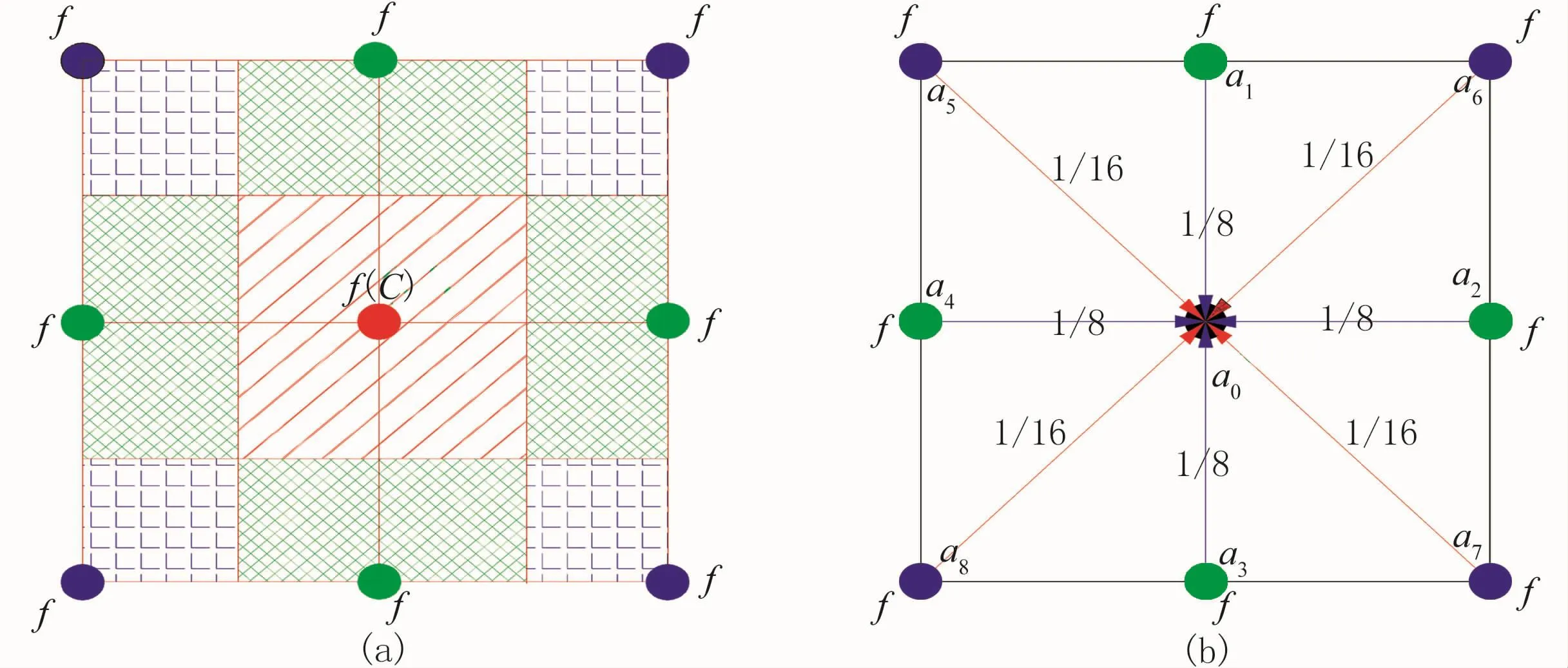
圖5 限制算子設計（面積率）示意圖

限制算子的作用是將細網格層經過松弛迭代后的殘差投射至較粗網格層，粗網格層上每一個網格節點及其周圍，有9個細網格層節點與其對應（圖5），殘量由細網格層投射至粗網格層過程中，細網格層上節點對粗網格對應節點的“貢獻”不同，當前，限制算子較多的采用完全加權算子，其設計思想一般采用面積率，即將某一粗網格進行16等分，設a為每個粗網格面積的1／16，則其上每一細網格節點對粗網格的“貢獻”可以歸納為：a0=4a，a1=a2=a3=a4=2a，a5=a6=a7=a8=a，a0、a1、a2、a3、a4、

a5、a6、a7、a8分別表示粗網格周圍對應的細網格點，如圖5所示，基于此，完全加權算子簡化為

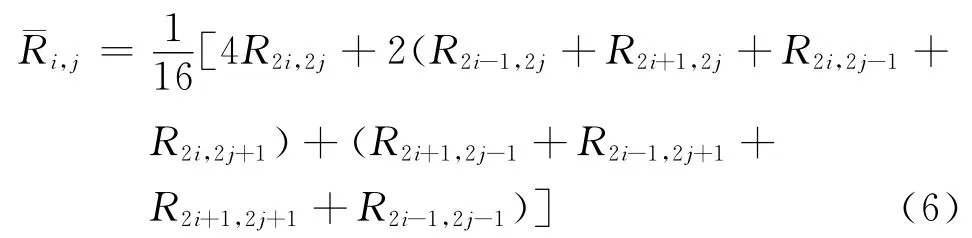
式中下標i，j代表網格節點編號。式（6）用矩陣的形式表示為

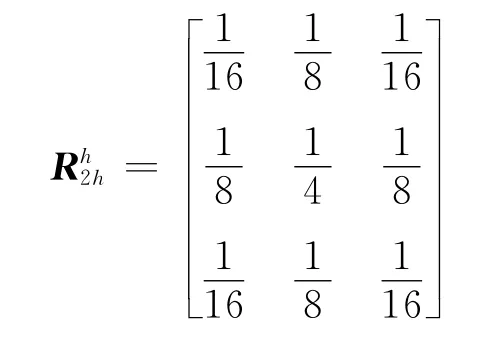
5.3 插值算子

插值算子將解的修正量從粗網格傳遞至細網格，算子構建原則是與粗網格相對應的細網格點值保持不變，其余細網格點值由其相鄰粗網格點值進行算術平均得到，即

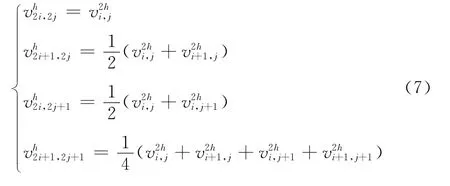
式中：v為網格節點解的近似量；上標h、2h分別表示細、粗網格層。基于式（7），可得 MG法的粗、細網格層間插值算子

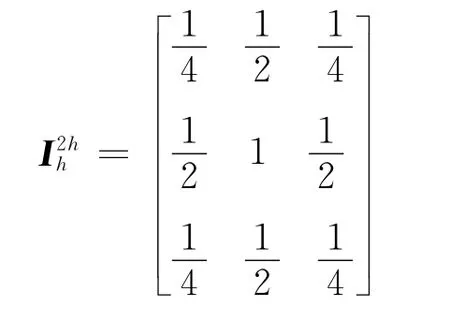
5.4 模型計算

設計模型電阻率為10Ω·m，向下極限深度為1.0×105m，考慮到Gauss-Seidel等一般迭代算法在計算過程中存在收斂性不穩定的缺陷，本次大地電磁二維正演模擬采用了收斂性較穩定的雙共軛梯度法（Bicgstab），多重（二重）網格算法的細網格松弛迭代算法也采用Bicgstab算法。正演模型采用二維均勻半空間模型，橫、縱向網格數均為20，為提高計算精度，設計單元網格長為50，寬為10，最大迭代次數為10000，誤差限為1.0×10-20。分別采用Bicgstab算法和多重網格算法（細網格松弛迭代采用Bicgstab算法）對模型進行計算，模型響應如圖6所示。由圖可知，Bicgstab算法在計算精度方面較多重網格算法有一定優勢。

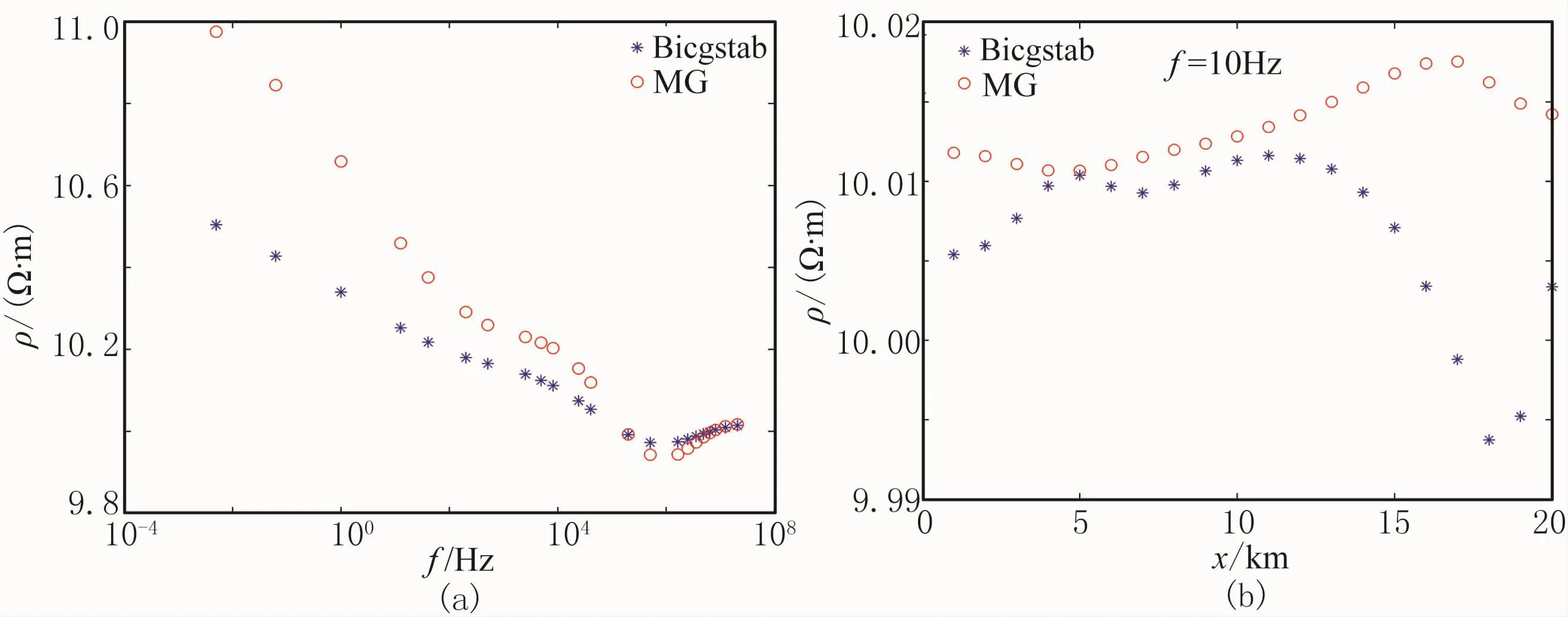
圖6 大地電磁二維正演模型響應示意圖

Bicgstab算法的計算時間為8.003234s，MG算法的計算時間為4.01562s，由此可見，MG算法在計算時間方面有明顯優勢。

6 結論和認識

本文采用 MG、SOR、PCG法，研究了二維Helmholtz方程的Dirichlet邊值問題的計算精度和收斂速度，并在此基礎上，初步研究了均勻半空間條件下基于MG法的大地電磁二維正演模擬響應，取得了如下認識。

（1）MG法的迭代收斂速度與網格尺度無關，且最初幾次迭代的收斂速度明顯優于其他算法。

（2）MG法在網格單元個數較少時，相同誤差限條件下的計算時間優勢并不明顯；在網格單元個數較多時，計算時間最多只是其他算法的一半；

（3）本次MG法的網格剖分采用不規則三角網格算法，導致采用網格層間插值和限制算子放大了計算誤差，進而使該算法的計算誤差較其他三種算法大，如何降低誤差有待進一步研究。

［1］ 劉小軍，王家林，陳冰等.二維大地電磁數據的聚焦反演算法探討.石油地球物理勘探，2007，42（3）：338-342.Liu Xiaojun，Wang Jialin，Chen Bing et al.Discussion on focus inversion algorithm of 2-D MT data.OGP，2007，42（3）：338-342.

［2］ 王青平，白武明，王洪亮.多重網格在二維泊松方程有限元分析中的應用.地球物理學進展，2010，25（4）：1467-1474.Wang Qingping，Bai Wuming，Wang Hongliang.Multigrid finite element analysis for 2D modeling of Poisson equation.Progress in Geophysics，2010，25（4）：1467-1474.

［3］ 何繼善，李帝銓，戴世坤.廣域電磁法在湘西北頁巖氣探測中的應用.石油地球物理勘探，2014，49（5）：1006-1012.He Jishan，Li Diquan，Dai Shikun.Shale gas detection with wide field electromagnetic method in Northwestern Hunan.OGP，2014，49（5）：1006-1012.

［4］ 胡祖志，陳英，何展翔等.大地電磁并行模擬退火約束反演及應用.石油地球物理勘探，2010，45（4）：597-601.Hu Zuzhi，Chen Ying，He Zhanxiang et al.MT parallel simulated annealing constrained inversion and its application.OGP，2010，45（4）：597-601.

［5］ 魯晶津，吳小平，Klaus Spitzer.三維泊松方程數值模擬的多重網格方法.地球物理學進展，2009，24（1）：154-158.Lu Jingjin，Wu Xiaoping，Klaus Spitzer.Multigrid method for 3D modeling of Poisson equation.Progress in Geophysics，2009，24（1）：154-158.

［6］ 韓波，胡祥云，何展翔等.大地電磁反演方法的數學分類.石油地球物理勘探，2012，47（1）：177-187.Han Bo，Hu Xiangyun，He Zhanxiang et al.Mathematical classification of magnetotelluric inversion methods.OGP，2012，47（1）：177-187.

［7］ Airaksinen T，Heikkola E，Pennanen A et al.An algebraic multigrid based shifted-Laplacian preconditioner for the Helmholtz equation.Journal of Computational Physics，2007，226（1）：1196-1210.

［8］ Mulder W A.A multigrid solver for 3D electromagnetic diffusion.Geophysical Prospecting，2006，54（5）：633-649.

［9］ Plaks A，Tsukerman I，Painchaud S et al.Multigrid methods for open boundary problems in geophysics.IEEE Transactions on Magnetics，2000，36（4）：633-638.

［10］ Zaslavsky L Y，Schlick T.An adaptive multigrid technique for evaluating long-range forces in biomolecular simulations.Applied Mathematics and Computation，1998，97（2-3）：237-250.

［11］ Tang J T，Wang F Y，Ren Z Y et al.3-D direct current resistivity forward modeling by adaptive multigrid finite element method.Journal of Central South University，2010，17（3）：587-592.

［12］ 柳建新，郭榮文，童孝忠.基于多重網格法的MT正演模型邊界截取.中南大學學報（自然科學版），2011，42（11）：3429-3437.Liu Jianxin，Guo Rongwen，Tong Xiaozhong.Boundary truncation of magnetotelluric modeling based on multigrid method.Journal of Central South University（Science and Technology），2011，42（11）：3429-3437.

［13］ Mitsuhata Y J，Uchida T.3D magnetotelluric modeling using the T-Ωfinite element method.Geophysics，2004，69（1）：108-119.

［14］ Moucha R，Bailey R C.An accurate and robust multigrid algorithm for 2D forward resistivity modeling.Geophysical Prospecting，2004，52（3）：197-212.

［15］ William L B.A Multigrid Tutorial.Society for Industrial and Applied Mathematics，2000.

［16］ Liu Yuanqing，Yuan Jiansheng.A finite element domain decomposition combined with algebraic multigrid method for large-scale electromagnetic field computation.IEEE Transactions on Magnetics，2006，42（4）：655-658.

［17］ 高曉峰.2D-Delaunay三角網格的數據結構與遍歷.天津理工大學學報，2006，22（2）：66-70.Gao Xiaofeng.Data-structure and traverse of 2DDelaunay triangulation.Journal of Tianjin University of Technology，2006，22（2）：66-70.

P631

A

10.13810／j.cnki.issn.1000-7210.2017.01.023

楊振威，馮磊，趙寧，趙秋芳，楊雙安.多重網格法二維Helmholtz方程解算及其在電磁法正演模擬中的應用.石油地球物理勘探，2017，52（1）：167-172.

1000-7210（2017）01-0167-06

*河南省焦作市高新區世紀路2001號，454000。Email：zhaoning＠hpu.edu.cn

本文于2015年10月9日收到，最終修改稿于2016年11月4日收到。

本項研究受河南省教育廳重點基金項目（15A170008）和河南省博士后基金項目聯合資助。

（本文編輯：馮杏芝）

楊振威 博士，講師，1984年生；2007年本科畢業于河南理工大學獲地理信息系統專業學士學位，2010年畢業于中國礦業大學（北京），獲礦產普查與勘探專業碩士學位，2013年畢業于中國地質科學院，獲地球探測與信息技術專業博士學位；現在河南理工大學資源環境學院從事地球信息科學與技術專業的教研。