基于多尺度量子諧振子算法的相空間概率聚類算法

王梓懿，安俊秀，王 鵬

(1.成都信息工程大學 并行計算實驗室，成都 610225； 2.西南民族大學 計算機科學與技術學院，成都 610225)

(*通信作者電子郵箱86631589@qq.com)

基于多尺度量子諧振子算法的相空間概率聚類算法

王梓懿1，安俊秀1*，王 鵬2

(1.成都信息工程大學 并行計算實驗室，成都 610225； 2.西南民族大學 計算機科學與技術學院，成都 610225)

(*通信作者電子郵箱86631589@qq.com)

針對大型集群難以進行任務調度和資源分配的問題，提出一種基于多尺度量子諧振子算法的相空間概率聚類算法(PSPCA-MQHOA)。首先，將集群工作狀態投影到相空間中，把復雜的集群工作狀態轉化為相空間中的點集；進而，將相空間網格化，形成多尺度量子諧振子算法(MQHOA)以處理離散目標函數；最后，利用MQHOA優化過程中波函數變化的概率解釋對集群節點進行概率聚類。PSPCA-MQHOA繼承了MQHOA物理模型明確、搜索能力強、結果精確等優點，并且由于以相空間作為離散化的目標函數，迭代次數大大減少。實驗結果表明PSPCA-MQHOA能適用于多種負載狀態的集群。

概率聚類；量子諧振子；相空間；波函數；集群

0 引言

隨著云計算技術的大面積普及與應用，集群的規模將越來越大[1]；同時節點間頻繁的遷移、備份、失效處理等高耦合性操作對集群的任務調度和資源分配造成了巨大的困難[2-4]。一種有效的處理方案是：把集群節點按照工作狀態聚類，同一聚類中的節點具有相同的負載狀態，如CPU占用率、內存占用率、I/O吞吐量、磁盤空間、網絡通信狀態等。文獻[5]運用模糊聚類技術把計算機劃分成若干個能力均衡的邏輯集群；文獻[6]使用改進的C均值聚類算法計算出集群節點聚類中心和分類結果。但是目前所有聚類算法都不能保證完全準確地把每一個實例劃分到合理的類，如果給出節點屬于各個類的概率來形成概率聚類，將有助于消除傳統聚類問題中硬性而快速的判斷方案引發的脆弱性[7]。在聚類的實際應用中已經有學者使用了概率模型[8-10]，然而使用概率模型對集群節點按工作狀態聚類的應用尚未見諸文獻。

對相空間理論的研究發現，傳統相空間同樣適用于云計算系統的分析。文獻[11]首次提出云計算相空間的概念，為分析云計算集群提供了思路；文獻[12]提出了多尺度量子諧振子算法(Multi-scale Quantum Harmonic Oscillator Algorithm, MQHOA)，其在收斂過程中波函數的特征對集群概率聚類具有啟發作用；文獻[13]基于MQHOA的高斯采樣提出了一種聚類中心選取算法，證明了MQHOA用于聚類的可行性，但該算法不適用于密度分布呈多峰特性的數據集。本文在相空間的基礎上利用多尺度量子諧振子算法的搜索聚焦能力，根據其收斂過程中波函數變化的概率解釋，提出了基于多尺度量子諧振子算法的相空間概率聚類算法(Phase Space Probabilistic Clustering Algorithm base on Multi-scale Quantum Harmonic Oscillator Algorithm, PSPCA-MQHOA)，并通過三種模擬集群實驗驗證了PSPCA-MQHOA能適用于多種負載狀態的集群。

1 相空間模型與多尺度量子諧振子算法

1.1 相空間投影與網格化

目前基于云計算相空間的研究已經有一定的成果[14-16]。文獻[11]給出了云計算相空間的一般定義：在云計算系統中以服務器的n個工作狀態參數為坐標軸所形成的n維空間稱為云計算系統的相空間。

對于只考慮兩個工作狀態x和y的擁有p個節點的集群，可以由相空間中的點集C表示：C={(xi,yi):i≤p}。某集群節點的CPU占用率和內存占用率在相空間中的投影如圖1所示，進一步將相空間劃分為n×n的網格，根據每個網格在相空間中的位置附加坐標，投影到相空間的節點就必然落入某一個網格中。

圖1 網格化相空間投影Fig. 1 Meshed phase space projection

將相空間如上述過程網格化后便可以運用MQHOA對節點進行聚類。如果把每一個網格當成一個點，落在網格中的節點數量當成函數值，整個相空間就可以抽象為一個離散的目標函數F(x,y)，其定義域為：1≤x≤n2, 1≤y≤n2(x,y為整數)。此時網格取代連續目標函數中的點成為最小的計算單位，落入網格中的節點越多視為更優的采樣位置，聚類的過程轉化為優化問題，網格劃分得越密計算的結果越精確。

1.2 多尺度量子諧振子算法在PSPCA-MQHOA中的應用

量子力學以其完備的理論成為現代物理學的基礎支柱之一，在多種技術中得到了廣泛的應用，其中量子諧振子的運動規律對優化問題有重要的啟示。多尺度量子諧振子算法(MQHOA)就是一種模仿量子諧振子從高能態向基態收斂過程的函數優化算法，文獻[17]詳細介紹了其物理模型。MQHOA的波函數表示了目標函數在定義域上最優解出現位置的概率密度，由算法在函數優化的收斂過程中高斯函數的疊加形成。文獻[12]給出了MQHOA在高維坐標分量xi的歸一化波函數公式:

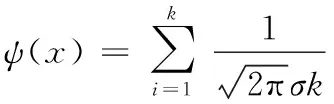
(1)

PSPCA-MQHOA的概率聚類過程就是尋找網格化相空間中局部包含節點最多的網格的過程，其波函數表示了網格化相空間中包含節點最多的網格出現位置的概率密度，以此波函數可以確定聚類個數,計算各網格中節點分屬于各聚類的概率。PSPCA-MQHOA過程可以視為MQHOA對一個離散目標函數的多峰優化過程。

2 PSPCA-MQHOA

2.1 PSPCA-MQHOA原理分析

如圖2為尺度收斂下采樣網格的移動情況，圖中網格中的數字表示被投影到該網格的節點數，被陰影覆蓋的網格為當前采樣網格，圖2(a)～(d)分別為尺度在12.5、6.25、3.125、1.562 5下的采樣網格位置，從中可以看出隨著算法尺度的收斂，采樣網格朝著局部節點數最多的網格聚攏。

圖2 尺度收斂下采樣網格的移動情況Fig. 2 Movement of sampling mesh under scale convergence

2.2 PSPCA-MQHOA基本流程

算法1 PSPCA-MQHOA。

輸入 集群狀態相空間,采樣網格個數k,采樣參數m,算法停止尺度σ,搜索尺度σs；

輸出 集群節點概率聚類的結果。

步驟1 把集群狀態相空間劃分為n×n的網格，隨機生成k個初始采樣網格。

步驟3 若k個采樣網格位置標準差變化量的最大值MAX(Δσk)滿足MAX(Δσk)≥σs,則返回步驟2，否則進入步驟4。

步驟4 若σs≥σ，搜索尺度減半σs=σs/2，返回步驟2；否則算法結束，此時的波函數圖像就表示集群的概率聚類。

PSPCA-MQHOA的迭代過程由嵌套的兩種收斂組成：多尺度收斂和量子諧振子收斂。其中多尺度收斂的次數在網格劃分完成后是固定不變的；對于量子諧振子收斂，后續的實驗表明其次數在同一尺度下通常為1。

2.3 算法結果分析

PSPCA-MQHOA的輸出結果為在停止尺度σ下的波函數，由于PSPCA-MQHOA的波函數表示了包含節點最多的網格出現位置的概率分布，所以波函數圖像波峰的位置就是節點數最多的網格最有可能出現的位置，即聚類的中心，波峰的數量則是聚類的數量。類似于量子諧振子處于基態時波函數由多個高斯函數疊加形成，此時的波函數由多個高斯函數在聚類中心處疊加形成。將組成波函數的若干個高斯函數分離出來單獨討論可知，每一個高斯函數都是由數個采樣網格在某處聚集形成，則此處必然是一個全局或局部節點數最密集的區域，自然地在這個區域就存在著一個聚類。若將每一個高斯函數代表一個聚類，那么高斯函數的函數值就是網格中節點屬于其代表聚類的概率貢獻，因此每一個網格中的節點都有屬于各個聚類的概率貢獻，將其歸一化后就得出了節點屬于各個聚類的概率。綜上所述，對算法輸出的波函數進行如下處理后形成了集群節點的概率聚類：

3 實驗分析

本章在二維相空間下對PSPCA-MQHOA進行實驗，對算法參數進行分析，以確定實驗中使用的算法停止尺度σ、采樣網格個數k和采樣參數m的選取；然后對三種模擬集群的工作狀態進行概率聚類實驗，輸出其波函數圖像，并與傳統聚類算法進行比較。

3.1 實驗參數的分析

PSPCA-MQHOA的精確性與網格的劃分有密切關系，網格劃分得越密算法的結果越精確，然而計算開銷越大。實際情況中需要根據集群中節點的數量動態調整網格劃分的密度，因此不詳細討論網格的劃分密度。為確定實驗參數使用的測試數據為擁有四個聚類中心的二維數據集，其在相空間的投影如圖3所示，并假設相空間劃分為n×n個網格，參數k、m、σ將以n的倍數進行取值。

3.1.1 算法停止尺度σ的分析與選取

算法停止尺度σ的取值直接關系著波函數的形態，σ取值過大則算法過早停止，波函數在聚類位置疊加次數不足，如圖4(a)所示為σ=n/2時波函數的俯視圖；σ取值過小則算法收斂過度，波函數在聚類中心處過度疊加，如圖4(b)所示為σ=n/30時波函數的正視圖。實驗的σ取值為n/2與n/30之間的一個合適的中間值σ=n/10，其波函數圖像俯視圖如圖4(c)所示。

圖3 四聚類中心測試數據集Fig. 3 Test data set with four clustering centers

圖4 σ不同取值下的波函數圖像Fig. 4 Wave function images with different values of σ

3.1.2 采樣網格個數k、采樣參數m的分析與選取

PSPCA-MQHOA參數k、m的選取會影響算法得到的聚類個數和聚類的位置。通過使用召回率(Recall)和精確率(Precision)來衡量k、m取值不同時算法測試結果的好壞。其中：召回率R側重于考查算法的查全率，計算方式如式(2)所示；精確率P側重于考查算法的查準率，計算方式如式(3)所示。

R=算法得出的與測試數據吻合的聚類數/測試數據的聚類數

(2)

P=算法得出的與測試數據吻合的聚類數/算法得出的所有聚類數

(3)

以相空間網格密度n的不同倍數對參數k、m進行取值，組成若干個不同的k、m參數組合，對測試數據進行聚類實驗，記錄10次實驗的平均召回率和精確率，如表1所示。從表1可以看出，參數k、m共同影響算法的召回率和精確率。當k較小時，算法的召回率較低，這是因為采樣網格數過少，無法全面覆蓋所有局部節點最多的網格；當m較小時，算法的精準率較低，這是因為算法以高斯采樣尋找更優網格的次數過少，采樣網格沒有完全聚集到局部節點最多的網格。隨著參數k、m取值的增大，算法的召回率和精確率趨近于1。理論上參數k、m越大算法越穩定，計算開銷也越大。同時考慮到算法的穩定性與效率，實驗參數k、m的取值為：k=n×1.5,m=n×2.0。

3.2 概率聚類實驗

實驗使用的數據為三種不同負載狀態下的模擬集群Cluster1、Cluster2、Cluster3。其中：Cluster1處于低負荷狀態；Cluster2處于負載不均衡狀態；Cluster3中有兩組節點負荷相似。它們在網格化的相空間投影如圖5所示。

表1 不同k、m取值下平均召回率和精確率Tab. 1 Average recall rate and precision rate of different k, m values

圖5 三種模擬集群相空間投影圖Fig. 5 Phase space projection of three simulated clusters

下面使用PSPCA-MQHOA對上述三種集群按工作狀態進行概率聚類，網格密度n為20，實驗參數為σ=n/10，k=n×1.5，m=n×2.0。算法輸出的波函數如圖6所示。從圖6可以看出，PSPCA-MQHOA的波函數圖像正好對應了集群節點的聚類情況，算法不僅可以應用在節點數量少、負載狀態單一的集群，對節點數量多、負載不均衡的集群也同樣適用，同時能區分集群中負載狀態十分相似的節點。

圖6 三種集群數據的波函數圖像Fig. 6 Wave function images of three clusters

在算法的兩種收斂中，量子諧振子收斂的次數由采樣網格移動情況與當前搜索尺度的關系決定，上述實驗中這種關系如圖7所示。從圖7中可以看出，采樣網格位置標準差變化量的最大值均小于當前搜索尺度，即每次量子諧振子收斂過程中，只需進行一次高斯采樣便可生成滿足條件的采樣網格，當前尺度下量子諧振子收斂次數為1。這是由于網格化的相空間是一個定義域取值范圍很小的離散目標函數，每次采樣后網格位置的變化都非常小。因此，PSPCA-MQHOA的性能只與網格劃分、集群工作狀態數量和參數k、m有關，與相空間的投影情況(即集群負載情況)無關。

圖7 采樣網格標準差變化量與搜索尺度的關系Fig. 7 Relationship between variation of standard deviation of sampling grid and search scale

使用2.3節所述的方法將集群節點進行聚類，并將聚類結果與經典聚類算法K-means和DBSCAN(Density-Based Spatial Clustering of Applications with Noise)進行比較，如表2所示，其中K-means算法在數據集Cluster1、Cluster2、Cluster3中K取值分別為1、3、2。

從表2可以看出：對于Cluster1，由于聚類只有一個，各算法的效果相當；對于Cluster2和Cluster3，K-means算法的效果最好，但K-means算法比較依賴K的設定。在不需要提前設定聚類個數的算法中，PSPCA-MQHOA的效果略好于DBSCAN算法。

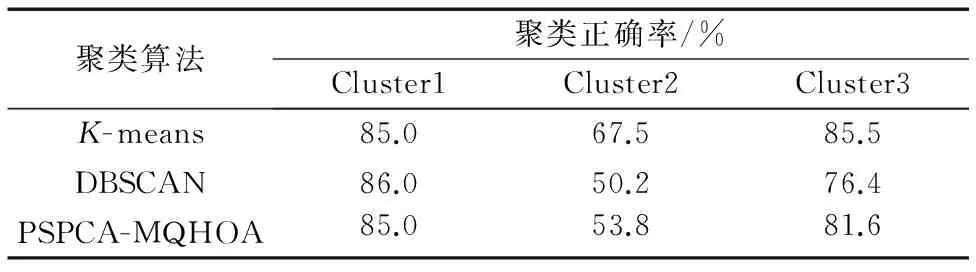
表2 不同聚類算法的正確率比較Tab. 2 Accuracy comparison of different clustering algorithms

4 結語

PSPCA-MQHOA將相空間離散化后作為MQHOA的目標函數，將普通的聚類問題轉化為MQHOA的多峰優化問題，并用波函數表示集群的概率聚類。通過對三種模擬集群的聚類實驗，驗證了PSPCA-MQHOA能適用于多種負載狀態的集群，并且算法具有迭代次數少、結果直觀明確等優點。使用波函數對集群節點進行概率聚類也給云計算系統分析、云計算監控、負載均衡調度等工作提供了新思路。

References)

[1] 陳康,鄭緯民.云計算:系統實例與研究現狀[J]. 軟件學報,2009,20(5):1337-1348. (CHEN K, ZHENG W M. Cloud computing:system instances and current research [J]. Journal of Software, 2009, 20(5): 1337-1348.)

[2] 李建鋒,彭艦.云計算環境下基于改進遺傳算法的任務調度算法[J]. 計算機應用,2011,31(1):184-186. (LI J F, PENG J. Task scheduling algorithm based on improved genetic algorithm in cloud computing environment [J]. Journal of Computer Applications, 2011, 31(1): 184-186.)

[3] 華夏渝,鄭駿,胡文心.基于云計算環境的蟻群優化計算資源分配算法[J]. 華東師范大學學報(自然科學版),2010(1):127-134. (HUA X Y, ZHENG J, HU W X. Ant colony optimization algorithm for computing resource allocation based on cloud computing environment [J]. Journal of East China Normal University (Natural Science), 2010(1): 127-134.)

[4] ERGU D, KOU G, PENG Y, et al. The analytic hierarchy process: task scheduling and resource allocation in cloud computing environment [J]. The Journal of Supercomputing, 2013, 64(3): 835-848.

[5] 劉伯成,陳慶奎.云計算中的集群資源模糊聚類劃分模型[J].計算機科學,2011,38(10A):157-160,168. (LIU B C, CHEN Q K. Fuzzy clustering partition model for computer cluster in cloud computing [J]. Computer Science, 2011, 38(10A): 157-160,168.)

[6] 姚婧,何聚厚.基于模糊聚類分析的云計算負載平衡策略[J].計算機應用,2012,32(1):213-217. (YAO J, HE J H. Load balance strategy of cloud computing based on fuzzy clustering analysis [J]. Journal of Computer Applications, 2012, 32(1):213-217.)

[7] WITTEN I H, FRANK E, HALL M A. Data Mining: Practical Machine Learning Tools and Techniques [M]. 3rd ed. San Francisco, CA: Morgan Kaufmann Publishers Inc., 2011: 285-287.

[8] MADDAH M, WELLS W M, Ⅲ, WARFIELD S K, et al. Probabilistic clustering and quantitative analysis of white matter fiber tracts [C]// IPMI 2007: Proceedings of the 20th International Conference on Information Processing in Medical Imaging, LNCS 4584. Berlin: Springer-Verlag, 2007: 372-383.

[9] VOGT J E, KLOFT M, STARK S, et al. Probabilistic clustering of time-evolving distance data [J]. Machine Learning, 2015, 100(2/3): 635-654.

[10] LU Z, LEEN T K. Penalized probabilistic clustering [J]. Neural Computation, 2007, 19(6): 1528-1567.

[11] 王鵬.云計算系統相空間廣義熱力學參數定義及分析[J].計算機應用,2012,32(8):2172-2175. (WANG P. Definitions and analysis of general thermodynamic parameters in cloud computing phase space [J]. Journal of Computer Applications, 2012, 32(8): 2172-2175.)

[12] 王鵬,黃焱,任超,等.多尺度量子諧振子高維函數全局優化算法[J].電子學報,2013,41(12):2468-2473. (WANG P, HUANG Y, REN C, et al. Multi-scale quantum harmonic oscillator for high-dimensional function global optimization algorithm [J]. Acta Electronica Sinica, 2013, 41(12): 2468-2473.)

[13] 燕京京,王鵬,范家兵,等.基于量子諧振子模型的聚類中心選取算法[J].電子學報,2016,44(2):405-412. (YAN J J, WANG P, FAN J B, et al. Clustering center selecting algorithm based on quantum harmonic oscillator model [J]. Acta Electronica Sinica, 2016, 44(2): 405-412.)

[14] 張磊,王鵬,黃焱,等.基于相空間的云計算仿真系統研究與設計[J].計算機科學,2013,40(2):84-86. (ZHANG L, WANG P, HUANG Y, et al. Research and design of cloud computing simulation system based on phase space [J]. Computer Science, 2013, 40(2): 84-86.)

[15] 郭又銘,王鵬,唐華,等.基于相空間的云計算專用監控系統[J].計算機工程,2013,39(7):40-44. (GUO Y M, WANG P, TANG H, et al. Specialized cloud computing monitoring system based on phase space [J]. Computer Engineering, 2013, 39(7): 40-44.)

[16] 王鵬,黃焱,李坤,等.云計算集群相空間負載均衡度優先調度算法研究[J].計算機研究與發展,2014,51(5):1095-1107. (WANG P, HUANG Y, LI K, et al. Load balancing degree first algorithm on phase space for cloud computing cluster [J]. Journal of Computer Research andt Development, 2014, 51(5): 1095-1107.)

[17] 王鵬,黃焱.多尺度量子諧振子優化算法物理模型[J].計算機科學與探索,2015,9(10):1271-1280. (WANG P, HUANG Y. Physical model of multi-scale quantum harmonic oscillator optimization algorithm [J]. Journal of Frontiers of Computer Science and Technology, 2015, 9(10): 1271-1280.)

This work is partially supported by the National Natural Science Foundation of China (71673032).

WANGZiyi, born in 1993, M. S. candidate. His research interests include distributed computing, intelligent algorithm.

ANJunxiu, born in 1970, M. S., professor. Her research interests include social computing, distributed computing.

WANGPeng, born in 1975, Ph. D., professor. His research interests include distributed computing, intelligent algorithm.

Phasespaceprobabilisticclusteringalgorithmbasedonmulti-scalequantumharmonicoscillatoralgorithm

WANG Ziyi1, AN Junxiu1*, WANG Peng2

(1.ParallelComputingLaboratory,ChengduUniversityofInformationTechnology,ChengduSichuan610225,China；2.SchoolofComputerScienceandTechnology,SouthwestMinzuUniversity,ChengduSichuan610225,China)

A Phase Space Probabilistic Clustering Algorithm based on Multi-scale Quantum Harmonic Oscillator Algorithm (PSPCA-MQHOA) was proposed to solve the task scheduling and resource allocation of large clusters. Firstly, the cluster operating status was projected into the phase space, and the complex working state was transformed into the point set in the phase space. Furthermore, the phase space was meshed to form the Multi-scale Quantum Harmonic Oscillator Algorithm (MQHOA) for discrete objective function. Finally, probabilistic clustering of cluster nodes was carried out by using the probability interpretation of wave function in the MQHOA process. PSPCA-MQHOA inherits the advantages of MQHOA, such as explicit physical model, strong search capabilities and accurate results, and it has few iterations due to the discretized phase space. Experimental results show that PSPCA-MQHOA can be applied to clusters in a variety of load conditions.

probabilistic clustering; quantum harmonic oscillator; phase space; wave function; cluster

TP393.027.2

A

2017- 02- 15;

2017- 03- 13。

國家自然科學基金資助項目(71673032)。

王梓懿(1993—)，男，廣西賀州人，碩士研究生，主要研究方向：分布式計算、智能算法； 安俊秀(1970—)，女，山西臨汾人，教授，碩士，CCF會員，主要研究方向：社會計算、分布式計算； 王鵬(1975—)，男，四川樂山人，教授，博士，CCF會員，主要研究方向：分布式計算、智能算法。

1001- 9081(2017)08- 2218- 05

10.11772/j.issn.1001- 9081.2017.08.2218