發掘函數級單指令多數據向量化的方法
李穎穎,高 偉,高雨辰,翟勝偉,李朋遠
(1.數學工程與先進計算國家重點實驗室,鄭州 450002; 2.信息工程大學,鄭州 450002;3.中國電子科技集團公司 第二十七研究所,鄭州 450047; 4.北京跟蹤與通信技術研究所,北京 100094)
(*通信作者電子郵箱xdsy213@163.com)
發掘函數級單指令多數據向量化的方法
李穎穎1,2,高 偉1,2,高雨辰1,2*,翟勝偉3,李朋遠4
(1.數學工程與先進計算國家重點實驗室,鄭州 450002; 2.信息工程大學,鄭州 450002;3.中國電子科技集團公司 第二十七研究所,鄭州 450047; 4.北京跟蹤與通信技術研究所,北京 100094)
(*通信作者電子郵箱xdsy213@163.com)
當前面向單指令多數據(SIMD)擴展部件的兩類向量化方法分別是循環級向量化方法和超字級并行(SLP)方法。針對當前編譯器不能實現函數級向量化的問題,提出一種基于靜態單賦值的函數級向量化方法。該方法首先分析程序的變量屬性,然后利用一組包括向量函數子句、一致子句、線性子句等編譯指示子句指導編譯器實現函數級向量化,最后利用變量屬性結果對向量化代碼進行了優化。從多媒體和圖像處理領域選擇部分測試用例對所提的函數級向量化的功能和性能在國產申威平臺上進行測試,與程序串行執行相比,采用函數級向量化后程序的執行效率更高。實驗結果表明函數級向量化可以取得類似任務級并行的加速效果,該方法可以指導自動函數級向量化的實現。
單指令多數據擴展;并行性;函數級向量化;編譯指示;靜態單賦值
0 引言
單指令多數據(Simple Instruction Multiple Data, SIMD)擴展部件通過一條SIMD擴展指令實現對SIMD向量寄存器中所有數據元素的并行處理,SIMD擴展指令集包括AltiVec、流媒體單指令多數據擴展(Streaming SIMD Extension, SSE)部件、先進的向量擴展(Advanced Vector Extension, AVX)部件、AVX- 512和NEON(ARM架構處理器擴展結構)等[1],國產處理器中龍芯[2]、飛騰[3]、申威以及魂芯[4]也都含有SIMD擴展部件,SIMD擴展部件現已廣泛應用于多媒體和科學計算等領域[5]。
雖然手工向量化理論上能夠實現最高程度的SIMD向量化[6],但程序員不僅要掌握程序的結構特征和數據布局,還要熟悉目標處理器底層結構和指令集的特點。SIMD自動向量化通過編譯器實現程序中可向量執行部分的挖掘,并自動生成面向目標處理器SIMD擴展的向量程序,極大減輕了程序員的工作負擔[7]。由于受到編譯技術的限制,當前編譯器僅從循環和基本塊兩個粒度挖掘程序中的向量并行性,編譯器還不能從函數這個粒度識別程序中的數據級并行[8]。當前的SIMD自動向量化方法主要從循環和基本塊兩個粒度發掘程序的向量并行性,循環級向量化方法與面向向量機的傳統向量化方法相似[9],對其的改進包括外層循環向量化[10]和多面體指導的多重循環向量化[11-12]。超字級并行(Super-word Level Parallel, SLP)是第一個發掘基本塊內向量并行性的方法[13]。
目前編譯器更多地是發掘循環中蘊含的數據級并行,但為保證正確性,一些情況下編譯器并不能把所有的循環都轉為向量執行,如:當循環內含有間接數組訪問和指針時編譯器不能將依賴關系分析清楚;此外當循環內含有函數調用時編譯器也可能向量化失敗[14]。
函數調用是循環向量化時的一個重大障礙。如下所示的數學庫自有函數代碼段的循環內含有一個函數調用sin,編譯器提供短向量數學庫可以對數學函數進行向量化,編譯器在作自動向量化時直接調用短向量數學庫中的向量版本sin,因此編譯器可以對帶有sin函數調用的循環成功地進行自動向量化。
#include
#include
#define N 128
double a[N]={0};
double b[N]={1,2,3};
double c;
int main(){
int i;
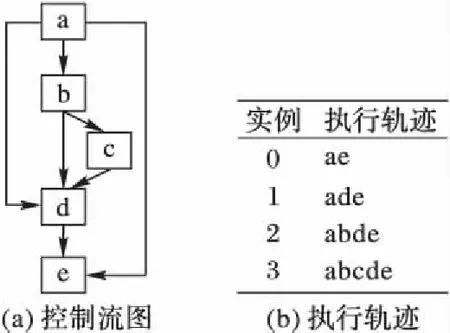
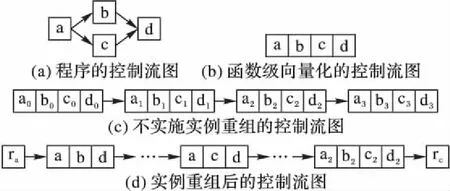
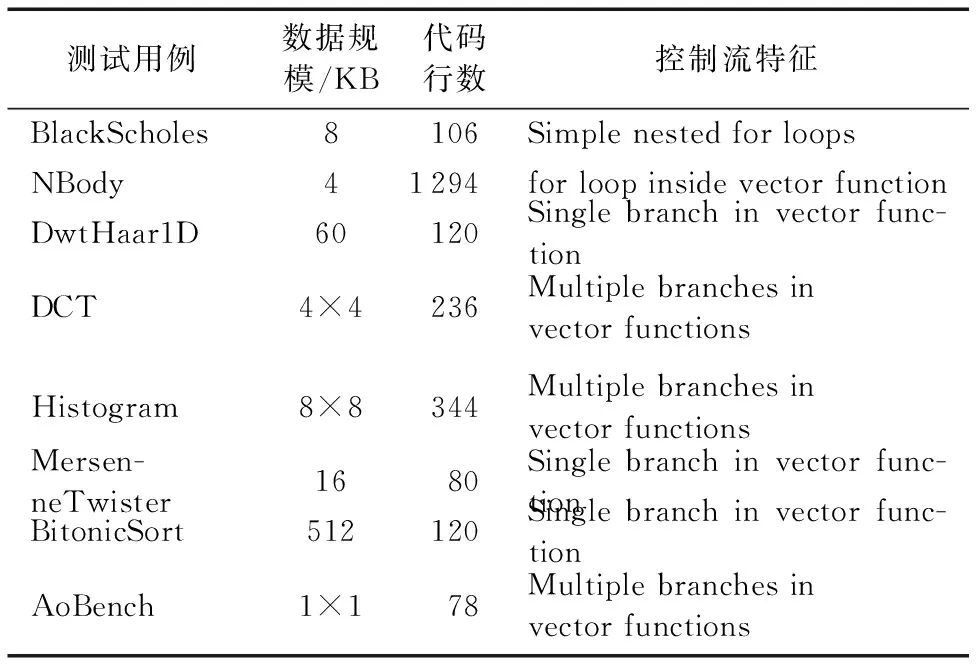
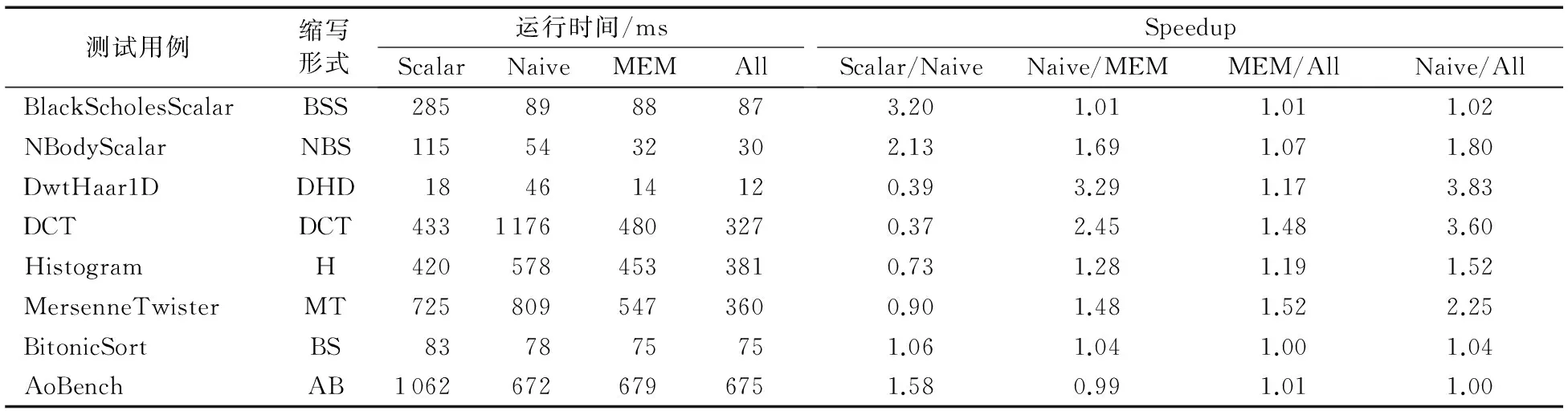
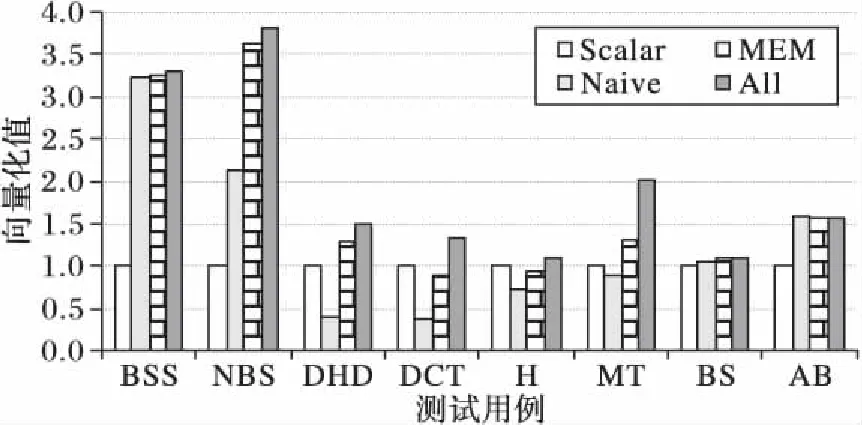
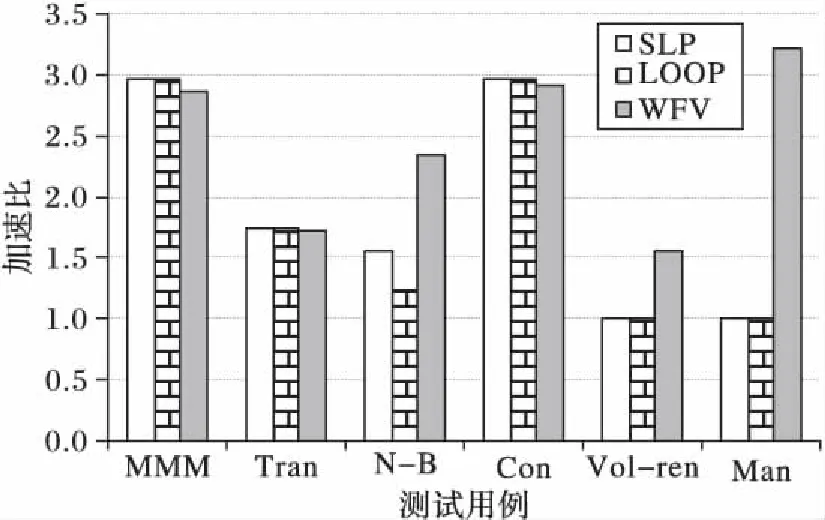
for(i=0;i a[i]=sin(c); } [swvec@cn09 test]MYM tswocc -O3 sin.c -simd=1 (sin.c:10)LOOP WAS VECTORIZED 然而當循環內含有一個用戶定義的函數調用時編譯器則不能成功地自動向量化。如下所示自定義函數代碼段的循環內含有一個用戶自定義的函數調用foo_sin,自動向量化時編譯器不容易分析清楚函數調用foo_sin會引用和修改哪些變量,除非在調用點上設置內聯,否則編譯器會保守地不實施自動向量化。 #include #include #define N 128 double a[N]={0}; double b[N]={1,2,3}; double c; double foo_sin(double p){ return sin(p); } int main(){ int i; for(i=0;i a[i]=foo_sin(c); } [swvec@cn09 test]MYM tswocc -O3 sin.c -simd=1 (sin.c:14)LOOP WAS NOT VECTORIZED,LOOP HAS CALLS 為了實現函數foo_sin的向量化,程序員可通過添加編譯指示指導編譯器完成函數級向量化,編譯器會根據標量函數foo_sin生成一個向量函數vfoo_sin,向量化后的循環內調用向量函數vfoo_sin代替原來的標量函數foo_sin,轉換過程的示意圖如圖1所示,假設SIMD擴展部件一次可以處理4個double數據,那么在向量化后的函數調用點處,每4個標量函數調用(foo_sin(x0), foo_sin(x1), foo_sin(x2), foo_sin(x3))由一個向量函數調用vfoo_sin( 圖1 標量函數轉為向量函數并在SIMD擴展部件上執行Fig. 1 Transfering scalar function into vector function and executing on SIMD extensions 本文提出了一種面向SIMD擴展部件的函數級向量化方法,與現有的面向循環和基本塊的SIMD向量化方法相比,本文的主要工作如下: 1)分析了函數級向量化的優點、合法性問題和變量屬性; 2)基于靜態單賦值形式實現了函數級向量化,并對生成的向量代碼進行了優化; 3)給出了一組SIMD擴展編譯指示,輔助編譯器發掘程序的函數級向量并行性。 1.1 函數級向量化的概念 函數級向量化是將幾個相鄰的計算實例合并為一個向量操作,實際上是一種單程序多數據模型(Single Program Multiple Data, SPMD),關于SPMD程序當前的研究大都基于統一計算設備架構(Compute Unified Device Architecture, CUDA) 或者開放運算語言(Open Computing Language, OpenCL)等編程模型,并且在圖形處理器(Graphics Processing Unit, GPU)上有硬件支持分歧等問題的處理。本文提出的函數級向量化是研究在SIMD擴展部件上運行SPMD程序,由于SIMD擴展部件上沒有硬件支持分歧的處理,因而加大了編譯的難度。 1.2 函數級向量化的優點 雖然內聯替換可以消除函數調用,但是過度的內聯替換不僅導致代碼膨脹同時也增加了編譯時間,因此完全利用內聯替換解決含有函數調用循環的向量化問題是不可行的,研究函數級向量化是必要的。當前的SIMD向量化方法是面向循環和基本塊發掘程序內蘊含的數據級并行,函數級向量化是從一個更大的粒度識別程序中的數據級并行,并可取得任務級并行的執行效果。循環級向量化方法有很多限制條件,如循環的迭代次數、非正規化的循環、依賴關系等,而這些可能不是函數級向量化的限制條件,函數級向量化相當于從另一個角度重新考慮程序向量執行。此外,函數級向量化還能處理任意復雜的控制流,因此循環級向量化方法不能成功向量化的代碼段,或許可利用函數級向量化實現向量執行。 1.3 函數級向量化的難題 候選函數的確定、合法性分析和分歧管理是函數級向量化時的三個難題。 1.3.1 候選函數的確定 判斷函數被調用次數是否足夠多,如果連續被調用的次數不足夠多則不能將其轉為向量執行,連續多次函數調用一般僅出現在循環體內。當程序中存在多個函數時,需要根據函數調用圖確定函數級向量化的順序。如果一個函數已經被發掘循環級或基本塊級向量并行性,那么進一步實施函數級向量化是困難的。 1.3.2 合法性分析 在對程序中的函數向量化時,保證向量化結果的正確性是困難的,因為需要考慮多個實例對應的函數體之間是否存在阻礙向量執行的依賴,這與編譯器中實現循環級向量化時考慮循環內的語句間是否含有依賴環類似,但是判斷循環內語句間是否存在依賴環在依賴關系分析中已經有很好的理論基礎,并且在編譯器中也有實現,而判斷多次函數調用之間是否有阻礙向量化的依賴是困難的,因為這涉及到編譯中過程間分析和別名分析兩大難題。 1.3.3 分歧管理 每一個實例不都是執行完全相同的指令,如圖2所示,控制流圖(Control Flow Graph, CFG)在4個輸入并行執行的情況下,產生執行軌跡。如實例1的執行軌跡為ade,而實例3執行的執行軌跡為abcde,這樣產生分歧的控制流使向量執行更為復雜。GPU的分歧管理是有硬件支持的,每一個實例都映射到多核處理器的一個標量核心,由一個中央控制單元控制不活躍實例的結果消除,而在SIMD擴展部件上要求顯式的向量執行,編譯時需要通過if轉換將控制流轉為數據流,然后借助SIMD擴展部件中提供的超字選擇指令實現謂詞執行,進而消除不活躍實例的結果。 圖2 不同實例執行的軌跡Fig. 2 Execution path of different instances 1.4 向量屬性分析 程序中的變量屬性分析包括一致(uniform)、連續(consecutive)、對齊(aligned)、保守(guarded)和不可向量化(nonvectorizable)等。基本塊的屬性包括全活躍(by_all)、混合(blend)、重連(rewire)、分歧(div_causing)屬性。 一個變量是一致的,當且僅當所有的實例中持有相同的值。變量的一致性可以對訪存和控制流進行優化。當控制流的判斷條件是一致標量時,編譯器可以意識到所有的執行代碼指令都會經過同一個路徑,這樣就可以減少分歧控制流帶來的掩碼執行開銷,只需生成超字條件跳轉指令即可;如果為一個直接尋址變量則直接利用廣播指令生成向量,而不需要利用插入指令逐個值插入到目標向量寄存器中以形成向量。 一個變量是連續的,當且僅當對于所有實例相鄰標識符的偏移量是連續的,當基址是一致的,偏移地址是線性連續單元時,編譯器可以生成更高效的連續向量訪存指令而不需要生成不連續的向量訪存如gather/scatter等指令。 一個變量是對齊的,當且僅當所有實例中的第一個實例的地址是SIMD擴展部件寬度 S的倍數。對齊的內存位置SIMD硬件通常提供更高效的向量內存操作,而不對齊的位置則可能需要兩次對齊訪存和一個拼湊操作,或者直接利用代價更大的不對齊訪存指令。 一個基本塊具有全活躍屬性,當且僅當該基本塊被所有的實例執行。如果基本塊具有by_all屬性,那么它不需要保守執行,因此將生成更高效的代碼。混合基本塊是指所有實例在這個基本塊內匯聚,分歧基本塊是指所有實例在這個基本塊內產生分歧。重連基本塊是指分歧基本塊的直接后繼或者與之不相交路徑的結束塊。分歧循環(divergent loop)是指實例在不同的迭代或一次迭代內的不同位置退出循環。 靜態單賦值形式(Static Single Assignment, SSA)是一種中間表示,它的單賦值特性表現在每個變量在這種中間表示中僅被賦值一次,SSA使得每個變量都有唯一的定義,因此數據流分析和優化算法可以更加簡單。若一個變量有M個定義和N個使用,若不采用SSA,則存在M×N個定義-使用關系,采用SSA則變為M+N。對同一個變量的不相關的若干次使用,在SSA形式中會轉變成對不同變量的使用,因此能消除很多不必要的依賴關系,如可消除多數輸出依賴和反依賴。由于SSA的中間表示有以上優點,因此本文基于SSA實現函數級向量化。 2.1 函數級向量化轉換 函數級向量化轉換算法包含四個步驟,分別是掩碼生成、選擇生成、控制流圖線性化和向量指令生成,算法的偽代碼如以下所示。 1)掩碼生成: Function CreateMasks(Block B) begin if B already has masks then return; end if B is loop header then createMasks(preheader); else foreach P∈predecessors do createMasks(P); end end createEntryMask(B); createExitMask(B); if B is loop header then createMasks(latch) if loop is divergent then Mask latchMask ←ExitMasks[latch→header] EntryMasks[B].blocks.push(latch); EntryMasks[B].values.push(latchMask); end end end 2)選擇生成: Function GenerateSelectFromPhi(Phi P,Block B) Begin S←P.values[0]; foreach i=1→P.values.size()-1 do Value V←P.values[i]; Block P←P.blocks[i]; Mask M←ExitMasks[P→B]; S←Select(M,V,S) in B; end replace all uses of P with S; delete P; end 3)控制流圖線性化: Function Linearize(Function F) Begin foreach B∈ F do foreach S∈ successors do if NewTargets[B→S].empty() then remove edge B→S; continue; end X←new Blocks; rewire edge B→S to B→X; foreach T ∈NewTargets[B→S]do P←NewTargetDivCausingBlocks[B→S][T]; create edge X→T under condition P; end end end end 4)向量指令生成: Function GenerateCode(Function F) begin foreach op∈function do if op is uniform then generate broadcast; else if op is consectuive then generate unit-stride memory access; else if op is nonvectorizable then generate sequential code; else if op is guarded then generate guarded code; else replace one by one end end end 2.1.1 掩碼生成 不同的實例執行時會在一些條件分支發生分歧,而SIMD擴展部件要求所有代碼都要執行,所以需要用掩碼顯式地指出哪些實例執行而哪些實例丟棄執行結果。在控制流圖中掩碼體現在基本塊之間的邊上。如果實例i的掩碼在控制流圖的邊A→B為真,那么表示實例i將會執行該分支,因此掩碼標志著向量化后向量中的相應元素是有效的數據,這種掩碼稱為邊掩碼,用A→B表示基本塊A到基本塊B的邊掩碼。邊掩碼隱含地定義了基本塊的入口掩碼。若是一個循環頭的基本塊,那么它的入口掩碼是一個來自進入循環的基本塊和循環尾部跳轉回來的基本塊的phi函數。 2.1.2 選擇生成 通過在控制流圖的匯聚點插入選擇操作,以丟棄不活躍實例產生的結果。將原控制流圖中的phi函數用選擇指令替換,具有n個值的phi函數可以替換成n-1個選擇指令。每一個循環要求一個結果向量保留離開循環的實例的循環活躍值,循環活躍值是跨越循環邊界的值,即在后續迭代中或循環外使用,可以認為是循環尾基本塊的活躍輸出變量。對每一個循環活躍值,結果向量通過一個phi函數和一個選擇操作兩條指令維持,這對于每個循環活躍值僅需插入一個選擇指令,而不需要考慮循環出口的個數。結果phi函數被放置在每個嵌套循環的前面,并且有兩個輸入值,來自循環頭的輸入值被頂級循環定義。對于嵌套循環,輸入值是父循環的結果phi函數,來自循環尾部的輸入值是結果更新操作。采用結果向量可以向量化所有循環,包括含有多層嵌套的控制流和多出口的循環。 2.1.3 控制流圖線性化 在所有的掩碼和選擇操作生成之后,控制流已經全部轉換為數據流,因此可以將控制依賴邊刪除。最終在保留原控制流圖執行順序的前提下將所有的基本塊線性執行。在原來的控制流圖中,如果基本塊A在基本塊B之前執行,那么在線性化后的控制流圖中,基本塊A也要放在基本塊B之前。如果控制流圖分裂為兩個分支,那么一條分支的所有基本塊必須完整地放在另一分支前面。控制流圖線性化的過程有很多策略,不同策略產生代碼的效率也不相同,實際中啟發式的方法可以考慮代碼規模或者寄存器的壓力。通過拓撲排序遞歸地決定基本塊的順序,最后控制流圖僅有一個入口和一個出口。 2.1.4 向量指令生成 控制流圖線性化后進入到向量指令生成階段,向量指令生成基本上是一對一的轉換,即將標量指令轉為向量指令,但是在向量指令生成過程中也需要考慮變量和操作的屬性。當變量具有一致屬性時,利用廣播指令將其轉為向量;當變量具有連續屬性時,可生成連續的向量訪存指令;當變量具有對齊屬性時,可生成對齊的向量訪存指令;對于不可向量化的操作如存儲指令和函數調用等需要復制多次。如果一個塊具有全活躍點屬性,它會被所有實例執行,因此不需要保守執行。 對于具有保守屬性的存操作,需要防止掩碼為假時將結果寫入內存。為防止實例為假時寫入內存,第一種代碼生成方法是構建if語句標量執行,但是這種實現方法引入了許多提取、插入和分支操作,降低了向量化收益。第二種代碼生成方法是利用“取-拼湊-存”組合操作,取出內存中的數據拼湊后直接存入內存中,對于連續存時此種方法比第一種向量化方法更高效。當不連續存時,如硬件支持生成聚集、分散操作會更高效,最后一種實現方法就是利用硬件支持的掩碼內存訪問。 2.2 函數級向量化優化 2.2.1 插入超字跳轉指令 在進入控制流圖線性化階段時,所有基本塊的入口掩碼和選擇操作select已經設置。此時,基本塊入口掩碼的值決定著整個基本塊指令是否執行。如果入口掩碼中所有實例的掩碼值均為假,那么可以跳過該基本塊的執行而直接執行下個基本塊。超字條件跳轉指令(Branches-On-Superword-Condition-Codes, BOSCCs) 分為兩類:一類是BOA(Branch-On-All),指所有分支都為真時跳轉;一類是BON(Branch-On-None),指所有分支都為假時跳轉。BOA指令發掘和BON指令發掘過程相似。BOA指令生成算法關鍵在于識別出一個超字條件所控制的指令區域,而經過掩碼生成和控制流圖線性化后,基本塊的入口掩碼已經確定并且基本塊已經按照線性順序組織在一起,因此,采用了線性掃描的方法將識別謂詞區域與增加條件跳轉操作一起進行。 2.2.2 轉為標量執行 如果函數中頻繁地有一個或者多個活躍的實例執行而其他實例的結果都被丟掉,那么可以利用實例多版本將其轉為串行執行收益可能更大。首先計算出活躍實例的索引,然后將該實例所有需要的值都提到標量寄存器中,最后將結果再更新到結果向量中。雖然標量執行時引入了插入和提取指令,但當向量代碼的開銷很大時實例多版本是有收益的。此外還可以對標量代碼使用SLP方法進行向量化,將同構操作繼續轉為向量操作。函數級向量化屬于水平向量化方法,而SLP方法屬于垂直向量化方法,首先需要將活躍實例中的值從原來的向量中提取出來,然后再繼續利用打包算法,但這個變換可能涉及到由于數據重組帶來的開銷。 下面的程序中顯示,對兩個活躍的實例,首先利用多版本技術將其轉為標量執行后再利用SLP方法發掘結果。原代碼中的兩個操作是相互獨立的,如while循環內的else分支所示。函數級向量化后如果僅有兩個實例是活躍的,首先計算得到索引的idx0和idx1,將兩個實例重新打包成向量,經過加法、減法和乘法等運算后將結果從向量中提取出來,更新到索引idx0和idx1中。 2.2.3 實例重組 假設函數被調用W次,向量化因子為V,函數被向量化后執行的次數為S,那么W、V和S之間的關系為W=V*S。與循環展開類似,S次向量函數調用可以放到一起,相當于向量函數體被執行S次,實例重組就可以在此情況下應用。實例重組就是將所有實例按照真值重新分為真假兩組,這樣在S次調用中僅有一次需要考慮分歧,而其余S-1次調用在重組后已經確認。實例重組的目標是改進代碼的一致性,包括控制流和訪存模式。假設程序的控制流圖如圖3(a)所示,函數級向量化的控制流圖如圖3(b)所示。如果W=16,V=4,那么S=4,在不實施實例重組的情況下控制流圖如圖3(c)所示。圖3(d)表示實例重組后的控制流圖,其中僅有1次調用需要考慮執行塊b還是塊c這個分歧,而其余3次調用時已經確定或者執行塊b或者執行塊c,其中塊ra和re表示重組代碼。 圖3 實例重組示意圖Fig. 3 Instance restructuring schematic diagram 編譯器自動地發掘程序內蘊含的函數級向量并行性是困難的,為了保證函數級向量化的正確性,本文提供一套編譯指示幫助編譯器實現函數級向量化。這套編譯指示不僅包括實現函數級向量化的子句,也包括對向量代碼優化的子句如一致子句、連續子句和對齊子句等。 3.1 向量函數子句 在選擇向量化哪個函數時,需要判斷其被調用的次數是否足夠多,如果被調用的次數不是足夠多,那么就是因為并行度不夠而不能被向量化,連續多次函數調用一般僅出現在循環體內。程序員在發掘函數級向量并行時,首先在循環外加一條指示#pragma simd vec-function,標記該循環雖然存在函數調用但是可以實現函數級向量化。編譯指示__decl-vec-function標記后面緊跟著待向量化的函數,編譯指示__decl-vec-function的格式如下: _ _decl-vec-function([(vector-clauses)]) vector-clause: uniform-clause linear-clause alignment-clause mask-clause 其中:uniform-clause表示一致子句;linear-clause表示線性之句;alignment clause表示對齊子句;mask-clause表示掩碼子句。下面的代碼中實現了函數mandel的向量化,首先利用編譯指示子句標記函數mandel是一個可向量化函數,同時在出現函數mandel的循環前面添加向量化編譯指示,實現了函數mandel的向量化。 _ _decl-vec-function(uniform(max_iter)) unsigned int mandel(complex c,unsigned max_iter); … for(int y=0; y< imageheight;++y){ #pragma simd vec-function for(int x=0; x< imageheight;++x){ count[y][x]=mandel(in_vals[y][x],max_iter); } } 編譯器通過識別函數和循環的向量指示子句實現函數的向量化,將函數由標量形式轉為向量形式,同時做好過程克隆。編譯器中也實現了變量的屬性分析,能夠識別出變量的一致性、連續性和對齊性等屬性,當指示子句給出的屬性和編譯器自動識別的屬性不一致時,根據指示子句給出的屬性生成向量代碼。 3.2 一致子句 一致子句表示向量寄存器中所有槽位的值相同,相反默認情況下認為所有實例對應的向量寄存器槽位的變量值不同。利用關鍵字uniform標記一致子句,一致子句格式如下: uniform-clause: uniform(uniform-param-list) uniform-param-list: parameter-name uniform-param-list, parameter-name parameter-name: identifier 3.3 線性子句 線性子句表示變量對應多個實例在內存中引用是連續的,用關鍵字linear表示。線性子句格式如下: linear-clause: linear(linear-variable-list) linear-variable-list: linear-variable linear-variable-list, linear-variable linear-variable: id-expression id-expression: linear-step linear-step: constant-expression linear-variable中的id-expression應該指派一個標量;linear-step中的constant-expression應該滿足或者是一個整數常數表達式,或者是整數類型的變量。如果一個linear-variable沒有對應的linear-step,則linear-step的值為1。如果linear-step為一個變量,并且這個變量在循環執行過程中被修改,這樣的行為被認為是未定義的。在向量屬性的上下文下,linear-step中的constant-expression也應該是整常數表達式,引用linear-step的參數是一致的。 3.4 對齊子句 對齊子句表示變量在內存中引用是對齊的,默認情況下認為變量是不對齊的,利用關鍵字alignment標記對齊子句,其格式如下: alignment-clause: alignment(uniform-param-list) alignment-param-list: parameter-name alignment-param-list, parameter-name parameter-name: identifier 對齊優化對于發揮SIMD硬件的性能也非常重要,編譯器生成更多的向量對齊訪問指令對于提升生成的向量程序執行效率有很大幫助,本文的編譯器中提出了向量對齊子句,為程序員提供一系列表達對齊的信息。 3.5 掩碼子句 默認情況下,對于每一個向量變體需要兩種實現:一種是調用時帶有掩碼條件,另一種是調用時不帶掩碼條件。如果程序中所有對該函數的調用都是帶條件的,則使用掩碼子句指導編譯器不生成不帶掩碼調用的函數體;反之,如果程序中所有對該函數的調用都是不帶條件的,則使用無掩碼子句,指導編譯器不生成帶有掩碼的函數體。掩碼子句格式如下: mask-clause: mask nomask 默認情況下編譯器會同時生成帶掩碼的向量函數體和不帶掩碼的向量函數體,同時使用掩碼子句和無掩碼子句是無效的。很多時候函數是在條件分支下被調用,如終止遞歸函數調用的執行,必須生成一個特別的帶掩碼版本的向量函數并且保證其正確執行。帶掩碼的向量函數有一個額外的bool型參數,函數體只有當掩碼值為真時才被執行。 將本文提出的函數級向量化方法在開源編譯器Open64中實現,編譯環境為Linux操作系統,版本為Redhat Enterprise 5。實驗時首先用Open64編譯器 將源程序轉化為向量化程序,然后再用基礎編譯器編譯成二進制代碼并在國產CPU 申威-1600上運行,最后用串行程序的運行時間除以向量化程序的運行時間便得到向量化的加速比。實驗平臺CPU主頻為2.0 GHz,內存為2 GB,L1數據cache為32 KB,L2 cache為256 KB,基本頁面為8 KB,向量寄存器的寬度為256位,可以同時處理4個浮點型數據或者8個整型數據。編譯器中還實現了訪存和循環等其他優化,通過在程序中添加函數向量化子句指導編譯器完成向量化,同時添加對齊、一致、連續等屬性指導編譯器生成更高效的向量代碼。添加函數向量化子句后編譯運行獲得向量化時間,關閉函數向量化子句后編譯運行得到未向量化時間,最后利用未向量化時間除以向量化時間得到函數向量化的加速比。 實驗分析包括兩部分,分別是優化測試分析和對比測試分析。優化測試分析主要描述訪存和控制流等優化對函數級向量化性能的影響;對比測試分析主要將本文提出的函數級向量化方法與現有的循環級和基本塊級向量化方法對比。 4.1 優化測試分析 從不同的應用領域選擇8個測試用例用于函數級向量化的優化分析測試。這些測試用例覆蓋了一系列現實應用,從排序算法到股票分析算法,從粒子運動模擬到圖形圖像處理。表1列出了這些測試用例的信息,包括輸入數據的規則、代碼行數、控制流特征和測試用例功能描述。 為了評估訪存和控制流等優化對函數級向量化的影響,比較不同優化方案下獲得的代碼。在不實施函數級向量化時即串行執行,用Scalar表示;將所有的性能優化分析都關閉,稱為直接函數級向量化,用Naive表示,直接函數級向量化時關閉所有的優化包括一致屬性和訪存操作屬性;訪存優化表示實施函數級向量化時加入了一致、對齊和連續屬性,實施了訪存優化,用MEM表示;All表示實施了本文提到的所有優化,包括訪存相關的一致、對齊和連續屬性分析,也包括本文提到的插入超字跳轉指令、轉為標量執行和實例重組等。 表2是不同優化方案下8個應用的運行時間,單位為ms。其中Speedup的Scalar/Navie表示Navie相對Scalar的加速比,其他依此類推;整體的觀察是隨著分析和優化的加入,性能在不斷增加。圖4顯示了不同優化方法對函數級向量化的性能測試結果。 表1 優化測試分析用例Tab. 1 Use-case of optimization test and analysis 表2 不同優化的運行時間對比Tab. 2 Running time comparison of different optimizations 圖4 不同優化的測試結果Fig. 4 Test results of different optimizations 1)直接函數級向量化(Scalar)。從表2與圖4中可以看出,與串行執行相比,即使直接函數級向量化(Naive)也能獲得不錯的性能加速,如BlackScholesScalar 的向量化加速比為3.20,NBodyScalar的向量化加速比為2.13。這些測試用例是數據密集型應用,帶有簡單的控制流,這樣的測試用例非常適合函數級向量化。然而,DCT的直接函數級向量化加速比僅為0.37,說明其直接函數級向量化的性能弱于標量執行性能,這樣的情況有4個例子出現。這種情況的主要原因是生成的向量代碼比較保守,所有的訪存操作都必須串行執行,所有含有副作用的操作都需要通過if語句生成,所有的控制流都被線性化,這說明了函數級向量化分析和優化的重要性。 2)加入一致、對齊和連續屬性訪存優化的函數級向量化(MEM)。保留一致性證明是有效的,與直接實施函數級向量化相比,加入一致和連續屬性的優化獲得的加速比為1.65。對于程序DwtHaar1D、DCT和 NBody,加入一致、對齊和連續屬性后,獲得了更好的加速效果,但它們的核心內仍有大量的操作保持標量。DwtHaar1D的一個重要性能提升是sqrt操作的參數轉為了一致屬性,如果這個函數調用沒有被標記為一致屬性,在直接實施函數級向量化中,它會被保守地執行,因此需要串行執行并且加入條件。連續屬性對程序DCT有很好的效果。 3)實施所有優化,包括訪存相關的一致、對齊和連續屬性分析,也包括本文提到的插入超字跳轉指令、轉為標量執行和實例重組等。本文最后的優化方案是將所有的優化手段都用上,這包括在控制流圖線性化階段保留部分控制流圖,這些控制流圖被證明實例不會分歧,這樣可以使得更少的代碼被執行,向量寄存器壓力更小,掩碼開銷更少。例如在程序Histogram中,循環內存在一個store操作,保守情況下,它需要被串行執行并且需要考慮分歧控制流的影響;然而,這個循環最后被證明不存在分歧,并且會被所有的實例執行。因此在向量化代碼生成時生成一個向量存指令,而不是幾條標量存指令。 實例多版本和實例重組方法對程序DCT、Histogram和MersenneTwister獲得了較好的加速效果,對這三個程序有效果的主要是因為控制流相關的提升,加速比分別為1.47、1.19和1.52。不過這三種優化對沒有分歧控制流的程序沒有任何優化作用,如程序BitonicSort。與實施一致和連續優化相比,實施多版本和實例重組后加速比平均為1.18。相比直接實施函數級向量化,采用訪存和控制流等優化手段后平均加速比為2.00,說明了訪存和控制流優化對函數級向量化性能提升有重要作用。 4.2 對比測試分析 從不同的應用領域選擇6個測試用例來測試函數級向量化的效果,選擇的測試用例包括矩陣乘、矩陣轉置和卷積等多媒體領域的典型程序,以及曼德伯特集、光線追蹤等圖像仿真程序。表3對選擇的測試用例進行了描述,包括數據規模、代碼行數、控制流特征和程序描述。 表3 對比測試分析用例Tab. 3 Use-case of comparison test and analysis 對選定的測試用例分別實施函數級向量化、循環級向量化和基本塊級向量化,測試分析不同向量化方法對選定測試用例的向量化效果,對比測試分析結果如圖5所示。圖5中函數級向量化方法的測試結果用WFV標記,循環級向量化方法的測試結果用LOOP標記,基本級向量化方法的測試結果用SLP標記。在實施函數級向量化時,已經添加了一致、連續等訪存優化和實例重組等其他優化。 圖5 對比測試分析結果Fig. 5 Results of comparison test and analysis 圖5的函數級向量化性能測試結果顯示加速比從1.56到3.22。其中Mandelbrot的加速比為3.22,Convolve的加速比為2.92,矩陣乘MMM的加速比為2.86,這3個程序的函數級向量化加速比較高是因為它們為簡單嵌套循環,并且不含有復雜的控制流。N-Body的加速比為2.34,Transpose的加速比為1.72,Volume rendering的加速比為1.56,這3個程序的函數級向量化結果加速比不高是因為它們含有復雜的控制流,在函數級向量化時為了處理分歧引入了許多選擇指令,帶來了較大的開銷,抵消了部分向量化收益;并且由于目標平臺不支持聚集、分散等高效的向量訪存操作,因此在代碼生成時還引入了大量的提取指令進一步抵消了函數級向量化收益。 函數級向量化方法能夠成功向量化Mandelbrot,而循環級向量化方法和基本塊級向量化方法都不能成功向量化Mandelbrot。這是因為Mandelbrot的最內層為while循環,循環退出條件不定。函數級向量化從一個更大的粒度,將整個while循環成功地進行了向量化。在對N-Body實施循環級向量化時,由于數據跨幅較大導致向量化收益被數據重組抵消較大部分,因此僅獲得了1.24的加速比;在對N-Body實施基本塊級向量化方法時,由于同構語句數量為3條同時還存在歸約操作,導致基本塊向量化方法不能充分利用向量寄存器,并且還存在額外的數據重組開銷,最后獲得了1.56的加速比;而在對N-Body實施函數級向量化時從一個更大的粒度向量化成功,因此獲得了2.34的加速比。對Volume rendering函數級向量化方法成功地實施了向量化,并獲得了1.56的加速比,而循環級和基本塊級向量化都沒有向量化成功。對比測試分析的三種向量化方法都成功地向量化了MMM、Convolve和Transpose,但是實施函數級向量化時由于過程間開銷導致函數級向量化效果略弱于基本塊級和循環級向量化方法,對于這3個程序基于循環展開的基本塊向量化方法和循環級向量化方法生成的向量代碼基本一致,因此獲得的加速比相近。 本文提出了一種發掘函數級SIMD向量化的方法:首先說明了函數級向量化的概念、優點和發掘函數級向量化時的主要問題;然后對函數級向量化時變量的屬性進行了分析,基于靜態單賦值形式實現了函數級向量化并對生成的向量代碼進行了優化;接著提出了一組編譯指示子句指導編譯器發掘函數級向量化,編譯指示子句包括向量函數子句、一致子句、線性子句等;最后從多媒體和圖像處理領域選擇了6個測試用例來驗證本文提出的函數級向量化方法的正確性和有效性。在國產申威-1600平臺上進行了性能測試,與程序串行執行相比,采用函數級向量化后程序執行效率比原來串行執行的效率更高。編譯器如何自動地實現函數級向量化的發掘以及對函數級向量化的代碼優化是下一步的研究工作。 References) [1] 高偉,趙榮彩,韓林,等.SIMD自動向量化編譯優化概述[J].軟件學報,2015,26(6):1265-1284. (GAO W, ZHAO R C, HAN L,et al. Research on SIMD auto-vectorization compiling optimization [J]. Journal of Software, 2015,26(6): 1265-1284.) [2] 彭飛,顧乃杰,高翔,等.龍芯3B的SIMD編譯優化及分析[J].小型微型計算機系統,2012,33(12):2733-2737. (PENG F, GU N J, GAO X, et al. SIMD compiler optimization and analysis based on Godson-3B processor [J]. Journal of Chinese Computer Systems, 2012, 33(12): 2733-2737.) [3] 陳書明,劉勝,萬江華,等.協同多核DSP YHFT-QMBase:體系結構及實現[J].中國科學:信息科學,2015,45(4):560-573. (CHEN S M, LIU S, WAN J H, et al. Coordinate multi-core DSP YHFT-QMBase: architecture and implementation [J]. SCIENCE CHINA (Informationis), 2015, 45(4): 560-573.) [4] 王向前,洪一,王昊,等.魂芯DSP的編譯器設計與優化[J].電子學報,2015,43(8):1656-1661. (WANG X Q, HONG Y, WANG H, et al. Compiler design and optimization for BWDSP [J]. Acta Electronica Sinica, 2015, 43(8): 1656-1661.) [5] CHEN L, JIANG P, AGRAWAL G. Exploiting recent SIMD architectural advances for irregular applications [C]// Proceedings of the 2016 IEEE/ACM International Symposium on Code Generation and Optimization. Piscataway, NJ: IEEE, 2016: 47-58. [6] LEI?A R, HAFFNER I, HACK S. Sierra: a SIMD extension for C++ [C]// WPMVP ’14: Proceedings of the 2014 Workshop on Programming Models for SIMD/Vector Processing. New York: ACM, 2014: 17-24. [7] HUO X, REN B, AGRAWAL G. A programming system for Xeon Phis with runtime SIMD parallelization [C]// ICS ’14: Proceedings of the 28th ACM International Conference on Supercomputing. New York: ACM, 2014: 283-292. [8] EVANS G C, ABRAHAM S, KUHN B, et al. Vector seeker: a tool for finding vector potential [C]// WPMVP ’14: Proceedings of the 2014 Workshop on Programming Models for SIMD/Vector Processing. New York: ACM, 2014: 41-48. [9] KENNEDY K, ALLEN J R. Optimizing Compilers for Modern Architectures: A Dependence-based Approach [M]. San Francisco, CA: Morgan Kaufmann, 2002. [10] NUZMAN D, ZAKS A. Outer-loop vectorization: revisited for short SIMD architectures [C]// PACT ’08: Proceedings of the 17th International Conference on Parallel Architectures and Compilation Techniques. Piscataway, NJ: IEEE, 2008: 2-11. [11] TRIFUNOVIC K, NUZMAN D, COHEN A, et al. Polyhedral-model guided loop-nest auto-vectorization [C]// PACT ’09: Proceedings of the 18th International Conference on Parallel Architectures and Compilation Techniques. Piscataway, NJ: IEEE, 2009:327-337. [12] KONG M, VERAS R, STOCK K, et al. When polyhedral transformations meet SIMD code generation [C]// PLDI ’13: Proceedings of the 34th ACM SIGPLAN Conference on Programming Language Design & Implementation. New York: ACM, 2013: 127-138. [13] LARSEN S, AMARASINGHE S. Exploiting superword level parallelism with multimedia instruction sets [J]. ACM Sigplan Notices, 2000, 35(5): 145-156. [14] WANG Y, WANG D, CHEN S, et al. Iteration interleaving-based SIMD lane partition [J]. ACM Transactions on Architecture & Code Optimization, 2016, 12(4): Article No. 58. LIYingying, born in 1984, M. S., lecturer. Her research interests include advanced compilation technique. GAOWei, born in 1988, Ph. D candidate. His research interests include high performance computing, advanced compilation technique. GAOYuchen, born in 1988, M. S. candidate. His research interests include advanced compilation technique. ZHAIShengwei, born in 1982, M. S., engineer. His research interests include advanced computing. LIPengyuan, born in 1989, M. S., researcher. His research interests include high performance computing. Methodforexploitingfunctionlevelvectorizationonsimpleinstructionmultipledataextensions LI Yingying1,2, GAO Wei1,2, GAO Yuchen1,2*, ZHAI Shengwei3, LI Pengyuan4 (1.StateKeyLaboratoryofMathematicalEngineeringandAdvancedComputing,ZhengzhouHenan450002,China;2.PLAInformationEngineeringUniversity,ZhengzhouHenan450002,China;3.The27thResearchInstitute,ChinaElectronicsTechnologyGroupCorporation,ZhengzhouHenan450047,China;4.BeijingInstituteofTrackingandTelecommunicationsTechnology,Beijing100094,China) Currently, two vectorization methods which exploit Simple Instruction Multiple Data (SIMD) parallelism are loop-based method and Superword Level Parallel (SLP) method. Focusing on the problem that the current compiler cannot realize function level vectorization, a method of function level vectorization based on static single assignment was proposed. Firstly, the variable properties of program were analysed, and then a set of compiling directives including SIMD function annotations, uniform clauses, linear clauses were used to realize function level vectorization. Finally, the vectorized code was optimized by using the variable attribute result. Some test cases from the field of multimedia and image processing were selected to test the function and performance of the proposed function level vectorization on Sunway platform. Compared with the scalar program execution results, the execution of the program after the function level vectorization is more efficient. The experimental results show that the function level vectorization can achieve the same effect of task level parallelism, which is instructive to realize the automatic function level vectorization. Single Instruction Multiple Data (SIMD) extension; parallelism; function level vectorization; compiler directive; static single assignment TP301.6; TP311.53 A 2016- 12- 29; 2017- 03- 21。 李穎穎(1984—),女,河南鄭州人,講師,碩士,主要研究方向:先進編譯技術; 高偉(1988—),男,黑龍江齊齊哈爾人,博士研究生,主要研究方向:高性能計算、先進編譯技術; 高雨辰(1988—),男,河南鄭州人,碩士研究生,主要研究方向:先進編譯技術; 翟勝偉(1982—),男,河南鄭州人,工程師,碩士,主要研究方向:先進計算; 李朋遠(1989—),男,河南焦作人,研究員,碩士,主要研究方向:高性能計算。 1001- 9081(2017)08- 2200- 09 10.11772/j.issn.1001- 9081.2017.08.2200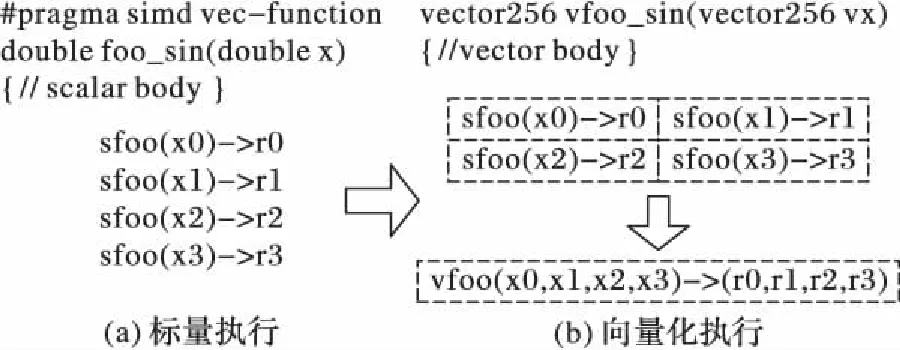
1 函數級向量化分析
2 基于靜態單賦值形式的函數級向量化

3 編譯器中實現
4 實驗結果與分析

5 結語

