淺談數形結合在數學中的應用
胡先莉 程魯
1 緒言
一直以來,我們的數學教育都是重視數學知識的傳遞與教授,而輕視了數學解題思想方法的詮釋與闡述。在漫長的實踐歷程中,人們運用各種各樣的數學方法、技巧或途徑來解決所遇到的問題,而在此過程中如果同一種方法、技巧或途徑被反復使用了多次,并且和想象中解題的效果一致,便成為了數學方法。即對一件事物的前后狀態、邏輯關系以及發展過程用數學語言表達出來,再對其進行演算和分析,以此來達到解釋和預言的目的的方法就是數學方法。而數形結合的主要思想就是以代數的嚴謹論證為主體并以圖形的直觀性為輔助來加以描述探究數學問題,使得論證的過程形象具體。合理的利用數形結合這一思想來解決一些比較抽象的數學問題,可以使解題過程更加清晰明了,而數學結合的核心也可以歸結為“以形助數,以數補形”八個字 。
2 數形結合的應用
2.1數形結合在函數中的應用
函數是初等數學中的重要知識,利用函數圖象等數形結合解決數學問題,就是將純粹的代數問題賦予其幾何意義,實現數到形的轉變,從而解決函數的最值,值域以及復合函數的定義域值域等問題。通常會采取的方法就是建立直角坐標系。
2.1.1數形結合在函數最值問題中的應用
對于函數最值問題的求法有:圖象法,基本不等式法,導數法,函數法等。所以當我們遇到無法用純代數方法解決問題時,就要考慮數形結合結合了。
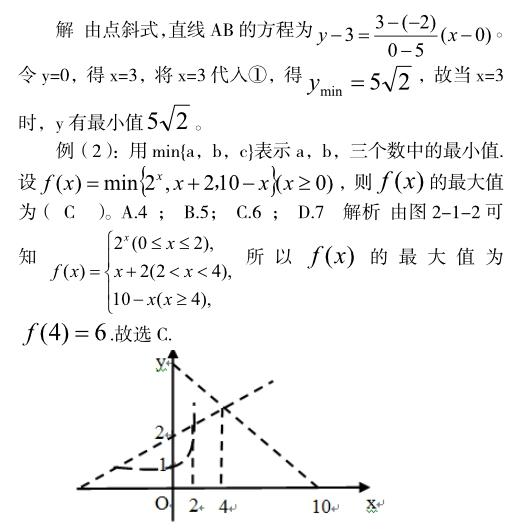
圖2-1-2
解題策略:本題結合了不等式組的線性規劃問題,所求f(x)為三個數中最小值中的最大值,如果單從代數角度去分析解決問題,必然會相當的復雜,但是借助圖形的話,就會非常直觀的看出x為何值時能取最大值。使得整個解題過程更加的清晰明了。
2.1.2數形結合在函數值域中的應用
求解函數的值域問題時如果利用數形結合的思想方法來求解無疑是將函數與圖形有機地聯合起來,再借助圖象的形象具體性求出函數的值域。利用此方法求解的題型特點是可以從這些函數的解析式中發現某種明顯的幾何特征,例如直線的斜率或者是兩點之間的距離公式等等,如果運用數形結合的方法來求解這些種類的函數問題,通常會更加方便容易,一清二楚。在實際生活中應用廣泛。


2.1.4數形結合在三角函數中的應用
三角函數的出現本來就是以幾何圖形為背景建立起數的概念,所以無論是在求解三角函數值還是在求三角函數的單調區間以及解析式等這類題型的時候,聯系起和圖形的關系都將是解題過程中不可或缺的一部分。
3 小結
本文對數形結合的特征、使用所遵循的原則、意義及其應用做了簡單的討論,對于比較抽象的數學問題通過數形結合都可以使其具體形象化。數形結合的思想是數學中基本而又重要的思想之一,它可以使人們從孤立地研究數量關系發展在變化過程中研究數量關系,使幾何學代數化;用代數方法研究幾何問題,同時也使某些代數問題幾何化,借助幾何學的成果研究解決代數問題,因而在我們的學習中,不能單純地學習知識,而要在知識的形成過程中,隨時注意滲透數形結合的思想,捕捉一切時機培養良好的思維品質。當然,在數學問題的解題中還有更多有趣的數學思想方法,還需要我們去不斷地努力探索、發現。
(作者單位:成都理工大學)

