一種圓形物體定位算法及在齒輪測量中的應用

盧 軍， 雷思鳴

(陜西科技大學 機電工程學院, 陜西 西安 710021)

一種圓形物體定位算法及在齒輪測量中的應用

盧 軍， 雷思鳴

(陜西科技大學 機電工程學院, 陜西 西安 710021)

考慮到實際的工業環境，需要對工件上的簡單幾何形狀區域進行高精度定位，因此提出一種基于物體幾何特征的定位算法，并以圓形定位為例對算法進行驗證。首先在邊緣提取的過程中根據待定位物體邊緣法向提出了新的邊緣檢測算法，并關聯模板匹配初定位結果動態的進行圓弧邊緣檢測，然后采用改進的隨機抽樣一致性算法進行圓擬合，使用該算法對PCB板上MARK進行了定位實驗驗證.最后針對傳統齒輪測量的不足，采用所提出的定位算法對齒輪的齒頂圓和齒根圓進行擬合，得到一系列齒輪參數.實驗表明，該算法能夠準確測量圓的輪廓，對齒輪的測量也達到一定的測量精度，驗證了算法的準確性與通用性.

邊緣檢測； 圓擬合； 動態測量； 齒輪參數測量

Abstract:According to the actual industrial environment,high precision positioning of the workpiece with a simple geometry is required.A localization algorithm based on geometric features of objects was proposed ,and verified by the example of circular positioning.First，in the process of edge extraction according to the location of object edge direction put forward a new algorithm of edge detection,and connect with the initial results of template matching to finish the arc edge detection dynamic.Second，the improved random sampling consensus algorithm was used to fit the circle,and to locate the MARK on the PCB board.Finally,using the proposed algorithm to fit the top circle and the root circle of the gear tooth to get a series of gear parameters aiming at the shortage of traditional gear measurement.The experimental results show that the algorithm can accurately measure the contour of the circle and reach a certain accuracy in measuring the gear,which verified the accuracy and versatility of the algorithm.

Keywords:edge detection; circle fitting; dynamic measurement; gear parameter measurement

0 引言

在手機制造業、激光精密焊等行業中，工業現場常常需要對直線、圓等一些簡單的幾何形狀進行高精度定位，模板匹配已經難以勝任其高精度要求，且由于工業環境復雜，都是大批量生產，同一物料的反光特性并不能保持一致，導致相機采集的同一物體圖像的灰度值差異大，并且一般的檢測定位算法沒有考慮實際的工業現場環境，穩定性差，常常把不感興趣的邊緣信息檢測出來，并不能滿足工業現場的要求.

齒輪作為廣泛應用于各個領域的一種機械傳動零件，在工業發展的歷程中發揮了重要的作用，齒輪本身的制造精度對整臺機器的使用壽命與工作性能有著最直接的影響，因此對齒輪的參數測量非常重要[1,2].因此，本文就目前傳統定位算法存在的不足，提出一種基于物體幾何信息定位算法，并以齒輪為實例對該算法進行了驗證.

1 幾何特征信息定位算法

現以圓形物體檢測定位為例進行介紹，算法在已知物體大致范圍下進行，即事先進行了初定位，預知了其粗略位置.

1.1 邊緣檢測

在灰度圖中，邊緣是圖像灰度值跳躍大的像素點的集合，是物體與背景的界限[3,4].物體與背景的邊緣具有高對比度.圖像中的邊緣主要有三種基本類型：階躍型邊緣、屋脊型邊緣、脈沖型邊緣，邊緣處的灰度值跳躍大，通常使用數學中的微分思想對圖像的邊緣進行檢測[5].常見的檢測算法有： Roberts算法、 Prewitt算法、 Sobel算法、 LoG邊緣檢測和Canny邊緣檢測，以上算法都為通用的邊緣檢測算法，在實際工業現場中環境復雜，傳統的邊緣檢測算法就顯得“力不從心”了，在檢測特定物體的邊緣時就顯得過于笨拙[6,7].以下闡述根據物體特定的幾何特征信息進行邊緣提取步驟，以圓形物體的邊緣提取為例.

(1)首先將輔助圓N等分，沿輔助圓半徑方向的等分點處創建測量矩形，矩形的高度為len1，寬度為len2，共有N個測量矩形，如圖1所示.

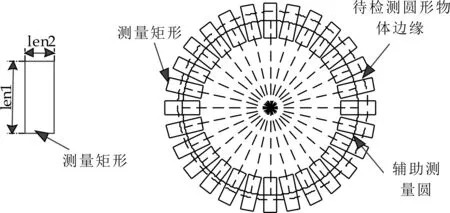
圖1 圓形物體測量矩形生成示意圖

(2)在每一測量矩形內沿著測量矩形方向計算矩形內每一像數點的導數，計算公式如式(1)所示.對于圓檢測，沿測量輔助圓半徑且遠離圓心的方向為測量矩形的方向，如圖2所示.根據求出的像數點的導數將檢測出的邊緣分為兩類，當f<0的邊緣為“黑到白”類；當f>0的邊緣為“白到黑”類，其判別公式如式(2)所示.再根據邊緣的梯度閾值去除“白到黑”類或“黑到白”類邊緣中的干擾邊緣，提取出感興趣邊緣，計算公式如式(3)所示.

(1)

(2)

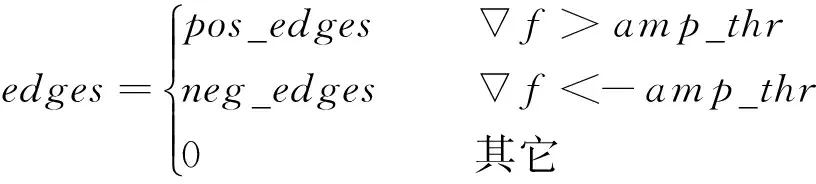
(3)

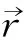
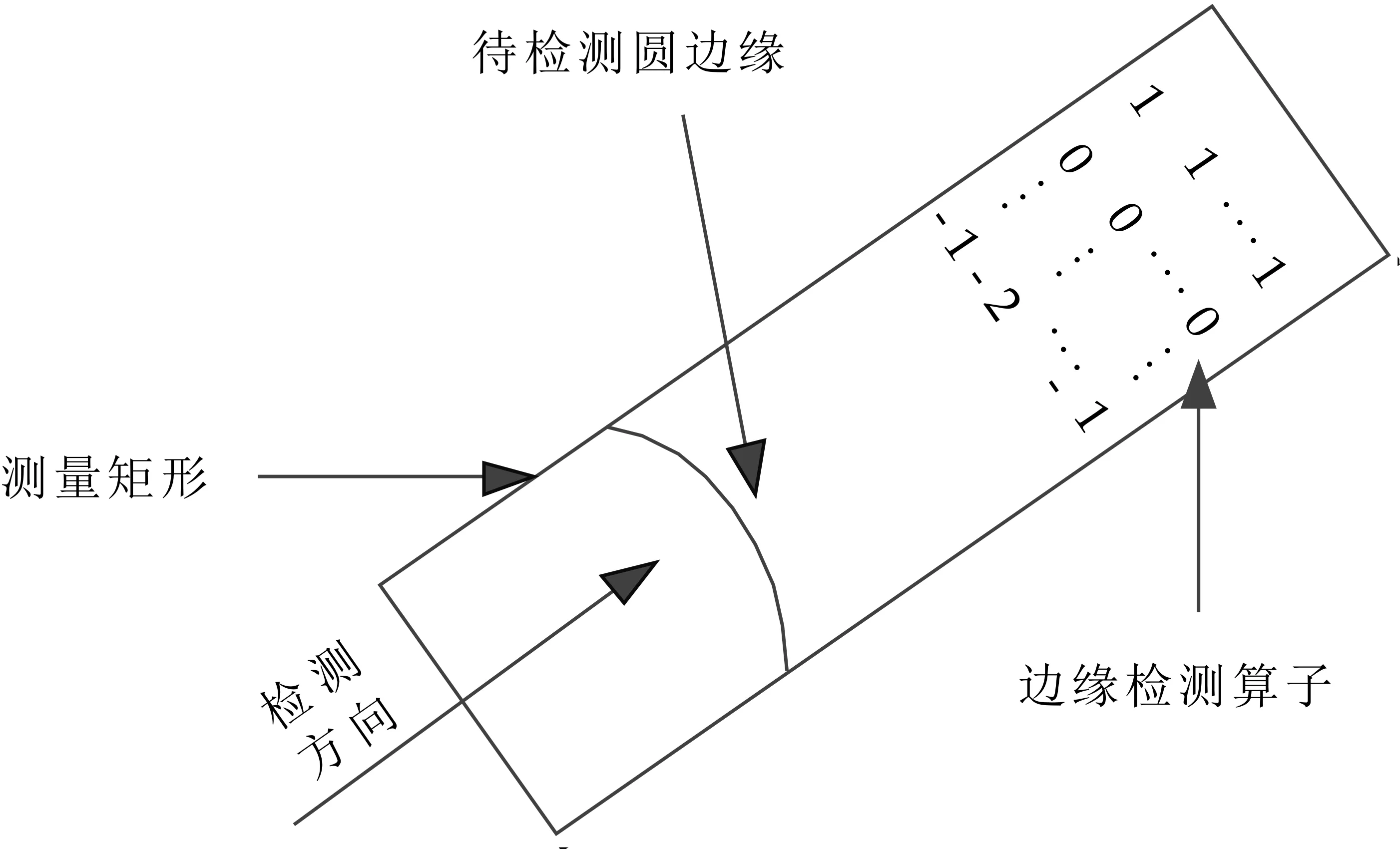
圖2 圓形物體邊緣檢測示意圖

1.2 圓弧邊緣擬合

最小二乘法是最常用的擬合算法，此方法對誤差符合正態分布的數據點很有效[8].但是在實際工業現場中經常會碰到一些干擾點，這些干擾點大多是偏向某一個方向的.從一個噪音較大的數據集中提取模型(比如只有20%的數據是符合模型的)時，這時采用最小二乘法擬合圓會存在很大誤差，得不到一個精準的結果.本文在隨機抽樣一致算法(RANSAC算法)的基礎上對其進行改進，可以有效的剔除噪聲點，準確檢測出圓，其算法具體描述如下.

(1)隨機從圓邊緣點集edges{P1,P2,P3,…,PN}中選擇三個點，記P1(x1,y1)、P2(x2,y2)、P3(x3,y3)，得到通過這三個點的圓方程Ax2+Cy2+Dx+Ey+F=0，其系數如式(4)、(5)、(6)、(7)所示進行計算.

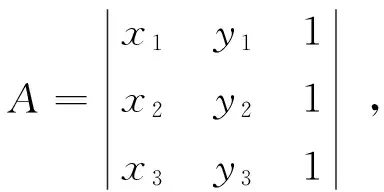
(4)

(5)

(6)

(7)

(2)用(1)中的方程去測試其余觀測點others_p{P1,P2,P3,…,PN-2}，由點P(x1,y1) 到圓心O(xc,yc)的距離di與圓半徑r之差的絕對值是否小于等于設定的距離閾值distance_thr，判別出觀測點Pi是局內點inliers還是局外點outliers，di的計算公式如式(8)所示、Pi的判別公式如式(9)所示.

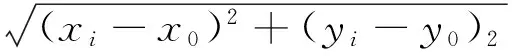
(8)

(9)

(3)如果局內點數與總點數的比值score大于等于算法預先設定的分數閾值score_thr時，并且局內點多于原有“最佳”圓的局內點，那么將這次迭代的圓設為“最佳”圓[9,10].

(4)重復(1)～(3)步n次，且n≤max_iter_count，直到找到最佳圓，并記下找到“最佳圓”時的局內點line_inliers{P1,P2,P3,…,Plm} ，max_iter_count為預先設定的最大迭代次數.

(5)使用最小二乘法對(4)中獲取到的“最佳”局內點集數據circle_inliers{P1,P2,…,Pm}進行圓擬合，求出最佳圓(x-xc)2+(y-yc)2=r2，計算公式如式(10)、(11)、(12)所示.

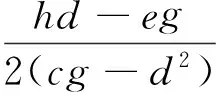
(10)

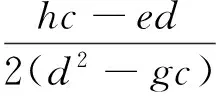
(11)

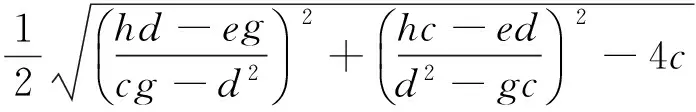
(12)

式(10)～(12)中：

1.3 動態測量定位

經過第一步和第二步后，可以準確的測量定位到測量矩形區域內的圓，但其測量范圍有限，有且僅當待測量定位物體在測量卡尺區域內，才有可能精準的測量定位到圓，因此，本文提出了基于模板匹配粗定位的圓測量定位，其與不使用模板匹配的初定位相比，增加了測量檢測范圍，更能適應工業自動化生產環境，其算法具體描述如下.

(1)首先使用灰度模板匹配對待測量定位圓進行初定位，并保存目標坐標Pref(xref、yref) 和角度angleref，并將其作為初定位參考信息.

(2)在目標坐標Pref(xref、yref)附近的點center(x0,y0)處創建半徑為r的測量輔助圓

ref_measure_circle{rect1,rect2,…,rectn}，

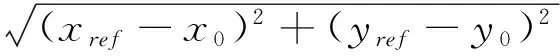
設置輔助圓上矩形卡尺數量num、卡尺高度len1、卡尺寬度len2，梯度閾值amp_thr、局內點判定閾值distance_thr和局內點分數閾值score_thr，并保存輔助測量圓位置、半徑信息、測量參數及擬合參數信息，記為測量模板.

(3)將(1)、(2)中的目標坐標、角度和測量參數信息作為動態測量定位算法的模板初始化信息，并假設初定位結果與測量輔助圓的相對位置在測量定位中始終不變.若P(x,y)、angle為t時刻初定位結果，則t時刻輔助測量圓measure_circle(rect1,rect2,…,rectn)，如公式(13)所示進行計算，關聯初定位動態測量示意圖如圖3所示.

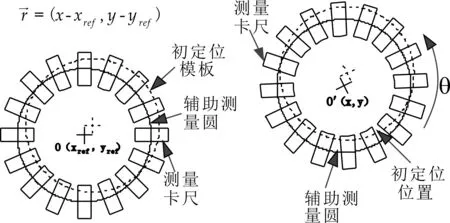
(a)創建模板時 (b)動態測量時圖3 關聯初定位動態測量示意圖

measure_circle=

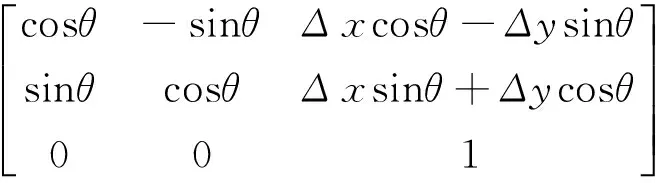
refer_measure_circle

(13)

式(13)中：Δx=x-xref;Δy=y-yref;θ=angle-angleref.

(4)根據(3)中獲取到的測量矩形卡尺位置信息和(2)中保存的測量參數及擬合參數信息完成t時刻的測量定位.

1.4 算法實驗

在本實驗中，將PCB板上圓形環作為測量定位目標，如圖4所示.首先使用圖4上的圓環區域創建初定位模板，如圖5所示，并保存初定位模板的初始坐標，圖6中的紅色“十字”中心為初定位模板的參考點.然后創建測量輔助圓，矩形卡尺數量30個，卡尺高度30像數，卡尺寬度5像數，梯度閾值50，局內點判定閾值3.5像數，局內點分數閾值0.7.最后將初定位模板參考點與輔助測量圓位置關聯，整個動態測量定位模板創建完畢.創建測量輔助圓及測量效果如圖7所示，部分測量定位結果顯示效果圖如圖8所示.

圖4 PCB板

圖5 初定位模板

圖6 初定位模板位置

(a)創建輔助圓效果 (b)矩形卡尺分布效果圖

(c)測量定位效果圖圖7 創建測量輔助圓及測量效果

圖8 部分測量定位結果顯示效果圖

在圖6中，紅色“十字”表示初定位結果，綠色圓表示測量定位到的圓，綠色圓上灰色“十字”表示使用改進的隨機采樣一致算法從檢測矩形中檢測出邊緣中提取出的局內點.從圖中測量定位效果顯示來看，當被定位目標發生較大的移動或旋轉時，該算法仍然能精準的定位到目標物體.相比模板匹配，能夠獲得更高的定位精度和穩定性，相比不使用模板匹配時，擴大了測量定位范圍，在自動化生產線上更能滿足現場要求.

2 齒輪測量

2.1 齒輪測量系統相機標定

齒輪圖象上每個點對應空間中齒輪表面上的每一點，像數點在圖象平面上的位置與齒輪上對應點的空間位置存在著幾何影射關系.這種關系由齒輪測量系統中攝象機成像的幾何模型所決定.這些參數必須由實驗與計算來確定[11]，如果實驗測得的攝像機內外參數不準確將會影響整個系統的測量精度.本實驗采用張正友標定算法進行標定.

2.2 齒輪圖像預處理

在對由相機獲得的圖像進行標定后，由于受到各種條件的限制和隨機噪點的干擾，標定后的圖像還不能直接進行齒輪參數測量，必須對圖像進行適當的預處理才能獲取到更精準的齒輪信息[12].

2.2.1 齒輪圖像濾波去噪

濾波的作用是最大限度的消除齒輪圖像中的噪聲而不破壞細節，對其檢測結果的準確性有非常大的影響.在齒輪圖像的獲取中，圖像的噪聲主要來自相機的噪聲[13]，對存在脈沖噪聲和椒鹽噪聲的圖像采用中值濾波去噪算法可以達到去除噪聲的目的而且還能夠保留圖像的邊緣細節，處理效果如圖9所示.

2.2.2 齒輪圖像二值化

齒輪圖像分割的目的是把齒輪區域與背景區域分離，以便對齒輪區域做進一步的分析，比如對齒輪輪廓的提取，對齒輪齒數的計數，因此齒輪圖像的分割對整個系統算法至關重要.

為了得到這些信息，需要將齒輪灰度圖像轉換為二值圖像，雖然灰度圖變為二值圖后丟失了很多信息，但二值圖像與灰度圖相比保留了更少的數據量，可以更方便有效地進行后續的處理，由于圖像中含有孔洞，在二值化基礎上根據漫水填充特性對圖片進一步處理，得到二值化圖像如圖10所示.

圖9 中值濾波處理效果圖 圖10 二值化圖像

2.3 齒輪參數的確定

在經過齒輪圖像采集、圖像處理之后，得到了比較理想的齒輪圖像，就可以進行參數測量了.在本實驗中，采用基于OpenCV 2.4.9+MFC對齒輪參數進行測量，如齒輪的齒頂圓、齒根圓、分度圓、模數、齒數、齒厚等.

2.3.1 齒頂圓和齒根圓的測量

齒頂圓直徑和齒根圓直徑的測量是后續參數測量的基準，需要準確的測量出齒輪的齒頂圓和齒根圓，才能對齒輪參數實現正確的測量.對所拍攝的齒輪圖片進行預處理后，利用上述所提出的物體幾何信息特征的測量方法對齒頂圓和齒根圓進行測量，得到齒輪的齒頂圓直徑da、齒根圓直徑df和齒輪的中心點.

2.3.2 齒輪齒數的確定

以齒輪的中心點為圓心，創建一個大于齒根圓直徑而小于齒頂圓直徑的圓形區域，如圖11所示.將圖11和圖10求取差集，如式(14)所示進行計算，差集效果如圖12所示.最后通過連通域標記算法對這些區域進行計數，即得到齒輪的齒數z.

diffent_image[i][j]=

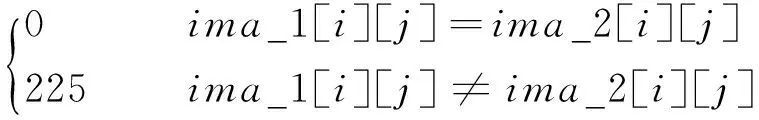
(14)

式(14)中：diffent_image[i][j]是所求圖中某一點像素；ima_1[i][j]是第一幅圖中某一點的像素；ima_2[i][j]是第二幅圖中某一點像素.

圖11 求齒數輔助圖 圖12 求取齒數

2.3.3 齒輪模數的確定

齒輪模數的確定需要根據已經測得的齒頂圓直徑和齒數來計算，根據已有公式(15)得到一個估計的模數，將計算得到的模數與標準模數進行比較，圓整后得到齒輪的模數m.

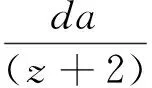
(15)

2.3.4 齒輪分度圓的確定

由以上計算得到齒輪模數、齒數，根據公式(16)得到齒輪的分度圓直徑d.

d=m×z

(16)

2.3.5 齒輪齒頂高、齒根高、齒厚的確定

由以上計算得到模數，對于本實驗中的標準齒輪來說，齒頂高系數ha*=1，頂隙系數c*=0.25，根據公式(17)和公式(18)得到齒輪的齒頂高ha和齒根高hf.

ha=m×ha*

(17)

hf=(ha*+c*)×m

(18)

對標準齒輪來說，分度圓上的齒槽寬和齒厚相等，由以上確定的模數，根據公式(19)得到.

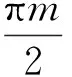
(19)

2.4 實驗測量時間

對于檢測效率進行多次測試，測試結果如表1所示.結果表明，該算法不僅測量速度快、而且精度高,滿足了齒輪常規參數測量的效率和功能要求.實驗在Intel(R) Core(TM) i5-4210U處理器，8 G內存，Windows 7 、64位操作系統的筆記本上進行，測試圖像為1 500萬像數(4 608 × 3 288)的彩色

齒輪圖像，被測試的算法版本為Release版.

表1 算法測量時間

2.5 實驗測量結果與誤差分析

為了驗證算法的可行性，對采集到的齒輪圖像進行標定后，應用本系統進行測量，圖像采集與測量界面如圖13所示，齒輪標準值與本系統測量值如表2所示.

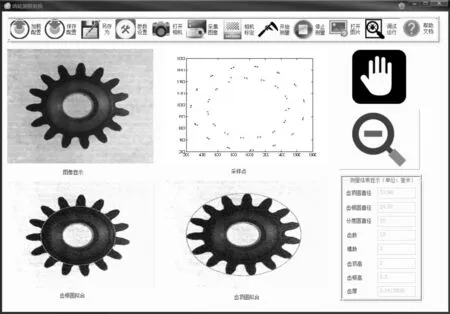
圖13 圖像采集與測量界面

參數齒頂圓直徑/mm齒根圓直徑/mm分度圓直徑/mm模數/mm齒數/個齒頂高/mm齒根高/mm齒厚/mm標準值34253021522.53.141592測量值33.9824.973021522.53.141587

從表2的測量結果可以看出，本測量系統對齒輪參數的測量與標準值還存在一定的差距，由于過程復雜，產生誤差的原因可能是多種的，具體分析如下：

(1)圖像采集設備誤差

由于實驗室攝像機分辨率較低，圖像采集質量不高，并且在成像過程中會產生一定的畸變，雖然已經通過標定有一定的改進，卻不能完全消除畸變，因此存在一定誤差.

(2)光源誤差

在實際的圖像采集過程中，光源的不均勻以及外界光源的干擾，從而影響到圖像成像質量，使得對齒輪輪廓的采集存在一定誤差.

(3)算法誤差

對同一張齒輪圖像采用不同的測量參數(矩形卡尺數量、卡尺高度、卡尺寬度、梯度閾值)和擬合參數(局內點判定閾值、局內點分數閾值)時，獲取到的采樣點數據不完全相同，最終導致擬合出的圓心坐標和半徑有誤差，實驗數據如表3所示.在表中使用了5組不同的測量參數和擬合參數定位測量同一張齒輪圖像的齒根圓，得到圓心X坐標的最大偏差(最大值-最小值)為0.011 6毫米，Y坐標的最大偏差為0.009 7毫米，半徑的最大偏差為0.008 2毫米.

(4)齒輪本身的制造誤差

在齒輪制造過程中，由于工藝誤差造成的齒輪誤差，使得真實齒輪并不是如同標準值那樣精確，因而在采用本系統進行測量時與標準值存在一定誤差.

表3 不同測量參數測量齒輪中心坐標與齒根圓半徑

3 結論

本文針對傳統的檢測定位算法存在的局限性，提出一種基于物體幾何特征的定位算法，此方法是沿物體邊緣法向的一種新的邊緣檢測方法，并對隨機抽樣一致性算法進行改進實現圓擬合.由于算法在測量前，需要進行初定位，因此，本文提出基于模板匹配的初定位算法，該算法增加了物體測量檢測范圍，更能適應自動化生產要求，其對特定幾何形狀的物體具有更好的檢測定位效果，以PCB板上圓形環作為測量定位目標進行驗證.最后將此算法應用到齒輪測量中，實現對齒頂圓和齒根圓的擬合，從而得到一系列的齒輪參數，不僅測量速度快、而且精度高,滿足了齒輪常規參數測量的功能要求，提高測量效率和準確率.

[1] 張景輝.基于機器視覺的直齒圓柱齒輪測量系統的設計與實現[D].天津：天津大學，2007.

[2] 景 敏，陳曼龍，楊 帆，等.基于機器視覺的螺紋參數綜合測量系統的設計[J].測控技術，2013，32(11)：35-38.

[3] Deriche R.Using canny′s criteria to derive a recursively implemented optimal edge detector[J].International Journal of Computer Vision，1987，1(2)：167-187.

[4] Mikolajczyk K，Schmid C.Scale & affine invariant interest point detectors[J].International Journal of Computer Vision，2004，60(1)：63-86.

[5] 張傳凱.基于機器視覺的LED芯片定位與檢測技術研究[D].西安：陜西科技大學，2016.

[6] Mangin J F，Rivière D，Coulon O，et al.Coordinate-based versus structural approaches to brain image analysis[J].Artificial Intelligence in Medicine，2004，30(2)：177-197.

[7] Kimmel R，Bruckstein A M.Regularized laplacian zero crossings as optimal edge integrators[J].International Journal of Computer Vision，2003，53(3)：225-243.

[8] Hast A，Nysj? J，Marchetti A.Optimal ransac-towards a repeatable algorithm for finding the optimal set[J].Journal of Wscg，2013，21(1)：21-30.

[9] Fischler M A.Random sample consensus：A paradigm for model fitting with applications to image analysis and automated cartography[J].Readings in Computer Vision，1987，24(6)：726-740.

[10] Isack H，Boykov Y.Energy-based geometric multi-model fitting[J].International Journal of Computer Vision，2012，97(2)：123-147.

[11] 于 泓.攝像機標定算法研究[D].濟南：山東大學，2006.

[12] 王文成.基于機器視覺的齒輪參數測量系統設計[J].機械傳動，2011，35(2)：41-43.

[13] 杜紅茹.基于機器視覺的齒輪尺寸測量問題研究[D].蘭州：蘭州理工大學，2011.

【責任編輯：蔣亞儒】

Aalgorithmforlocatingcircularobjectsanditsapplicationingearmeasurement

LU Jun， LEI Si-ming

(College of Mechanical and Electrical Engineering， Shaanxi University of Science & Technology， Xi′ an 710021， China)

2017-08-09

陜西省科技廳科技計劃項目(2016GY-049)

盧 軍(1961-)，男，陜西咸陽人，教授，碩士生導師，研究方向：智能機器人技術

2096-398X(2017)05-0156-06

TP24; TP27

A